基于CFD评估尺度效应对V型网板水动力的影响

刘景彬，唐 浩, ，许柳雄, ，孙秋阳，刘 伟，银利强，张 锋

1. 上海海洋大学 海洋科学学院，上海 201306

2. 大洋渔业资源可持续开发省部共建教育部重点实验室/国家远洋渔业工程技术研究中心，上海 201306

网板是单船拖网系统中实现网口水平扩张的重要构件，其水动力性能直接影响网具的滤水容积和捕捞效率[1]。为改善网板水动力性能，渔业科研人员通过海上实测、模型试验和数值模拟等方法[2-4]，致力于开发和优化不同类型的网板[5-6]。由于海上实测对网板进行全尺度试验不但费用高、耗时久，而且难以按照试验设计方法进行，因此实际操作中对网板的姿态和受力进行实物测量的研究相对较少[7]。为了能够在较短时间内通过比较系统的研究估算出网板的水动力性能，利用模型试验和数值模拟进行研究则是相对简便有效的方法[8-9]。

利用模型试验和数值模拟研究网板水动力首先要按照几何相似对网板进行等比例缩小，构建的物理模型需遵循雷诺准则进行试验。由于网板模型和实物不能同时满足雷诺定律和弗劳德定律，导致基于模型试验或者数值模拟计算得到的网板水动力性能预报值存在一定误差[10]。在网板水动力研究中，Park等[11]利用水槽试验对比了5种不同弯曲度立式曲面网板的水动力性能，认为底拖网网板弯曲度为15%时升力系数最大。Xu等[12]选用1∶1的尺度比，采用响应面法对矩形曲面网板的展弦比、弯曲度和最大弯曲度位置等参数进行优化，发现弯曲度是影响网板水动力的主要因素。优化弯曲度后，网板最大升力系数提高了20.5%。Chu等[13]按1∶1模型尺度对立式弧形V型网板进行三维建模，分析不同冲角、展弦比、板面夹角参数下的网板水动力性能，并运用计算流体力学 (Computational fluid dynamics, CFD) 对网板及周围压力分布进行了可视化分析。Xu等[14]选用1∶2的模型尺度比，对V型网板进行了水槽试验和数值模拟，结果显示展弦比为0.49，板面夹角为17°的网板性能最优。同时，通过对比两种计算流体力学软件Fluent和CFX模拟结果与水槽试验结果的差异，认为CFX对于升、阻力的预测更精准，升力的最大误差为15.4%，阻力的最大误差为15.2%。刘宏伟等[15]选用1∶10的模型尺度比，利用雷诺平均(RANS) 湍流模型中的标准 K-ω (Standard k-ω)模型，选用力矩系数来衡量网板的稳定性，对比了展弦比分别为1.5和2.0的矩形曲面网板的力学性能。结果表明，在0°～50° 冲角条件下，网板展弦比越大，其临界冲角和升力系数越小，且俯仰力矩系数由0.001变为0.013，说明网板的稳定性有所降低。模型试验验证表明，对于展弦比1.5的网板，其升力系数最大误差为14.7%，误差随着冲角的增加逐渐降低。Takahashi等[16]选用1∶10的模型尺度比，利用K-ε (Realizable k-ε) 进行数值模拟，结合水槽模型试验法对比研究了立式双翼开缝网板在不同冲角下的水动力性能，结果显示，数值模拟的最佳冲角为17.5°，最大升力系数为1.65；水槽模型试验的最佳冲角为20°，最大升力系数为1.64。You等[17]将神经网络与多目标遗传算法相结合，选择升、阻力系数做为目标函数，对尺度比为1∶10的网板模型进行结构优化，结果表明展弦比为2，弯曲度为13.6和15.4的两个网板模型的性能最佳。Matthew等[18]按照1∶1的模型尺度比构建了矩形网板和蝠翼式网板，探究了网板与海底底质的相互作用，通过在网板上安装“软刷”地面装置减少底质对网板的影响，结果显示安装地面装置的蝠翼式与矩形网板相比，底质对网板的影响相对减少了61%。

随着计算机技术的发展，运用CFD法研究水动力性能可大大提高工作效率。多数学者在研究网板水动力性能时构建物理模型选择的缩小尺度不同，很少考虑尺度比对网板水动力预测值精确性的影响。因此，本研究针对V型网板，采用RANS湍流模型中的K-ε模型进行数值模拟，对不同尺度比及不同厚度的网板模型进行水动力模拟。同时，根据该型网板海上作业的真实工况，模拟时设置了网板外倾10°的姿态，并在该姿态下改变不同的迎流冲角。对比分析了不同尺度比、厚度下的水动力模拟结果与动水槽试验结果之间的差异，以及不同尺度比下流场的差异，试验遵循雷诺准则，考虑雷诺效应对结果的影响来探究尺度效应对V型网板水动力的影响效果，研究结果可为构建网板物理模型的尺度确定以及模拟仿真研究提供科学参考。

1 材料与方法

1.1 网板结构参数

网板的外形结构见图1。原型网板为我国近海小型渔船的网板，实物网板尺度小，为了能在模型试验中有足够大的雷诺数范围，网板模型的尺度在三分力量程范围内应尽可能地放大一些。因此选择按3种尺度比 (1∶2、1∶3、1∶4) 和3种网板厚度 (2、5、10 mm)，通过实物模型制作了2块网板，三维建模3块网板，共设计5块网板。其中1#和3#网板为模型试验网板。网板的板面夹角(Γ)、翼展 (L)、翼弦 (C)、网板面积 (S)、展弦比(λ)等参数见表1。根据Xu等[14]的研究结果，该网板临界冲角约为40°，故将网板冲角范围设置为10°～60°，间隔为5°。试验遵循雷诺准则，为保证不同尺度网板试验时雷诺数相同，设置了不同的流速条件。

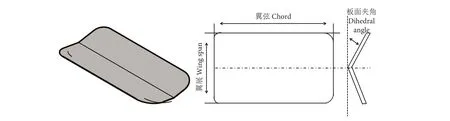
图1 网板参数结构示意图Fig. 1 Schematic diagram of structural parameters of otter board models

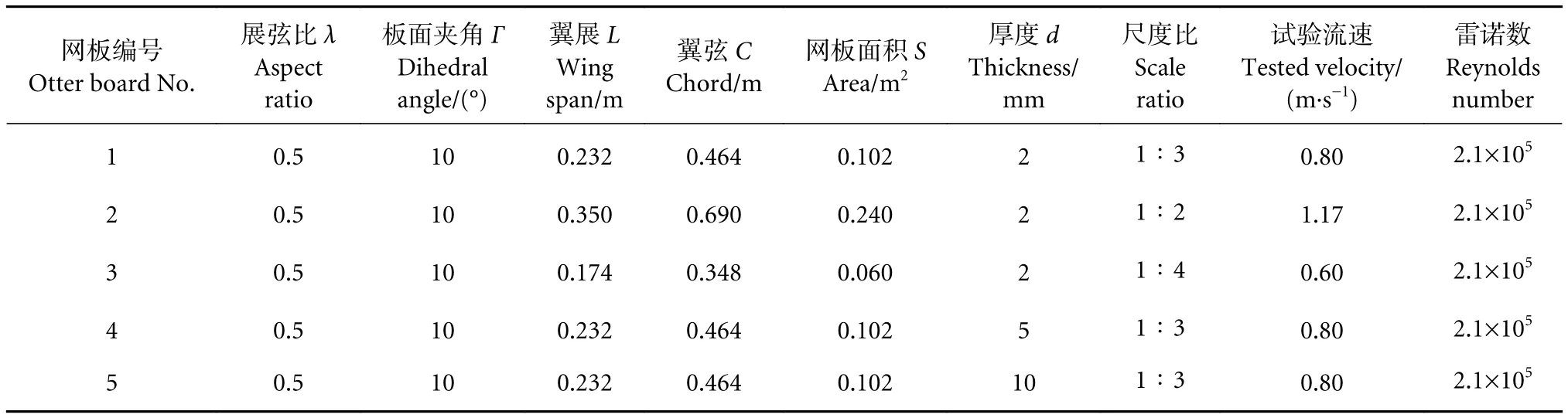
表1 网板编号及试验参数Table 1 Otter board number and experimental parameters

1.2 数值模拟

采用ANSYS 19.2软件进行数值模拟，在workbench中完成数值计算[19]。数值水槽尺寸的确定需考虑以下方面：1) 水槽的尺寸要保证网板后方流态的充分发展；2) 水槽壁面的边界效应对网板周围流态的影响[12-14]。若按照模型试验水槽尺度计算会增加巨大的计算量。因此，数值水槽尺寸以网板的特征长度 [翼弦长尺度 (C)、翼展尺度 (L)] 为标准建立为6.5C×2.6C×4.3L(图2)，通过水槽试验研究了相同流速下雷诺数最小的网板模型 (3#网板)60～120 cm·s-1的水动力系数与雷诺数的关系，发现流速范围的阻力系数Cd处于自动模型区内。试验为保持雷诺数相同，对3种尺度比网板分别设置对应的流速 1∶2 (117 cm·s-1)、1∶3 (80 cm·s-1)、1∶4(60 cm·s-1)。

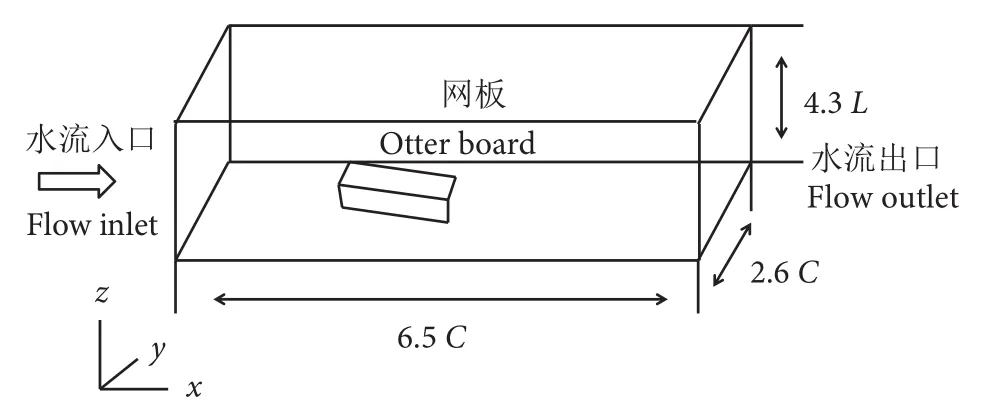
图2 模拟计算区域Fig. 2 Domain of simulation calculation

数值水槽和网板周围网格全部划分为四面体网格。网板面网格尺寸为6.5 mm，模拟计算区域网格最小尺寸为8.8 mm，最大尺寸为70 mm (图3)。在网板表面设置15层膨胀层增强壁面条件，第一层膨胀层厚度为9.9×10-2mm (通过计算得到网板表面y+≈9.4)，增长率为1.2[14]。计算区域总节点数和网格数分别为 1.5×106和 7.7×106。

图3 网板冲角为40°时周围网格划分Fig. 3 Computational grid partitions around otter board at angle of attack of 40°

研究中假设流体为不可压缩流体，控制方程包括连续方程 (1)和N-S方程 (2)，采用有限体积法( Finite volume method, FVM) 对控制方程进行离散，湍流模型选择可实现的K-ε模型，并选用压力梯度效应增强壁面处理[20-21]。数值水槽出口压力设置为0 Pa，湍流强度为5%。网板和数值水槽壁面设置为无滑移。计算为稳态计算，选择SIMPLE作为求解方法。

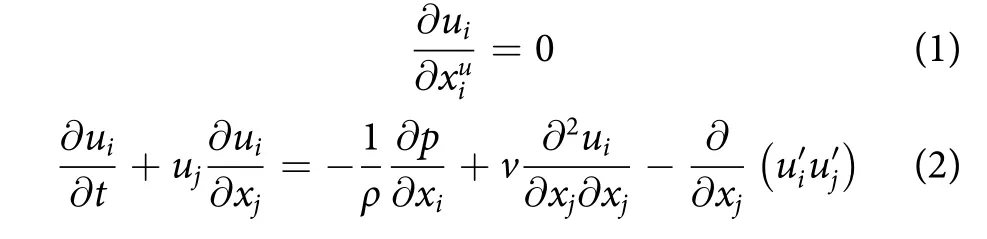
式中：ν为流体的动力黏度 (N·s·m-2)；t为时间(s)；ρ为流体密度 (kg·m-3)；p为压力 (N)；μ为黏度系数；ui、uj为流体速度分量 (m·s-1)。网板水动力性能相关参数有升力Fl、升力系数Cl、阻力Fd、阻力系数Cd、升阻比K。雷诺数Re相关计算公式如下：

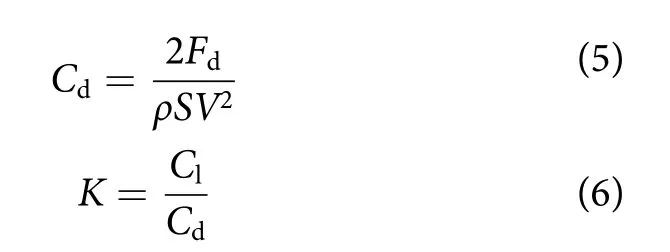
式中：ρ为流体密度 (kg·m-3)；S为网板投影面积(m2)；V为水流速度 (m·s-1)；l为特征长度 (m)；Cl为网板升力系数；Cd为网板阻力系数；Fd为网板阻力 (N)；Fl为网板升力 (N)；K为升阻比。

1.3 水槽模型试验

为验证数值模拟计算结果，于2021年6月在上海海洋大学动水槽中进行了1#和3#网板模型试验，水流速度分别设置为80和60 cm·s-1。动水槽配有六分力传感器 (量程为20 kg，精度为0.5%)，试验水温为23 ℃，水的密度为997.5 kg·m-3，测量并记录稳定状态下30 s内的平均值。将网板姿态设置为外倾10°，并在外倾的基础上设置不同的水流冲角 (10°～60°，间隔 5°) 进行试验 (图 4)，并用相机记录试验过程。

图4 网板模型动水槽试验Fig. 4 Flume tank test of otter board model

2 结果

2.1 水槽试验验证

相同流速下3#网板的雷诺数最小，因此选择其验证水动力系数是否在自动模型区内。水槽模型试验时利用公式 (3)—(5) 计算得到尺度比为1∶4的V型网板 (3#网板) 升力系数、阻力系数在不同冲角下和雷诺数的相互关系 (图5)，升、阻力系数随着雷诺数的增大基本保持恒定，可见网板水动力相关系数均进入自动模型区，其雷诺数为2.1×105～4.2×105，对应水流速度为 60～120 cm·s-1。

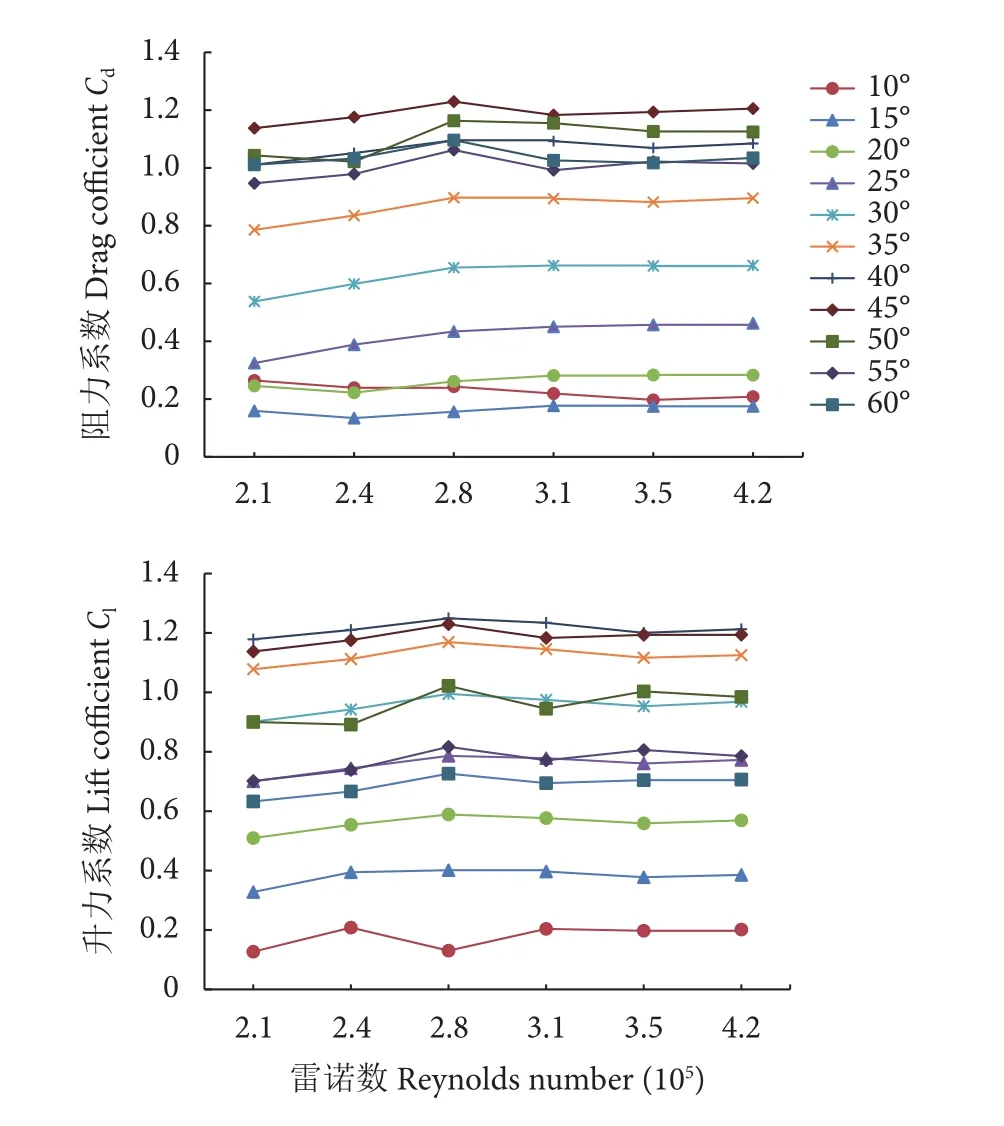
图5 V型网板不同冲角下的升力系数、阻力系数与雷诺数的关系Fig. 5 Relationship between lift coefficient, drag coefficient and Reynolds number of V-type otter board at different angles of attack

水槽试验中测试了V型网板 (1#网板) 在外倾10° 姿态下，迎流冲角从 10°～60° 的水动力系数，水流速度80 cm·s-1。对比试验结果与模拟结果，验证数值模拟的可靠性。模型试验和数值模拟的阻力系数结果吻合较好，45° 冲角之前，阻力系数均随着冲角的增加而增大；在冲角达到45° 后，阻力系数出现一个先减小后增大的趋势，最大阻力系数分别为1.229和1.138；模型试验和数值模拟升力系数结果吻合较好，均随着冲角的增加，先增大后减小。模型试验在40° 时取得最大升力系数1.249，数值模拟在40° 时取得最大升力系数1.178；冲角小于30° 时，升力系数的模拟值高于试验值。冲角达到30° 后，升力系数试验值高于模拟值(图 6)。

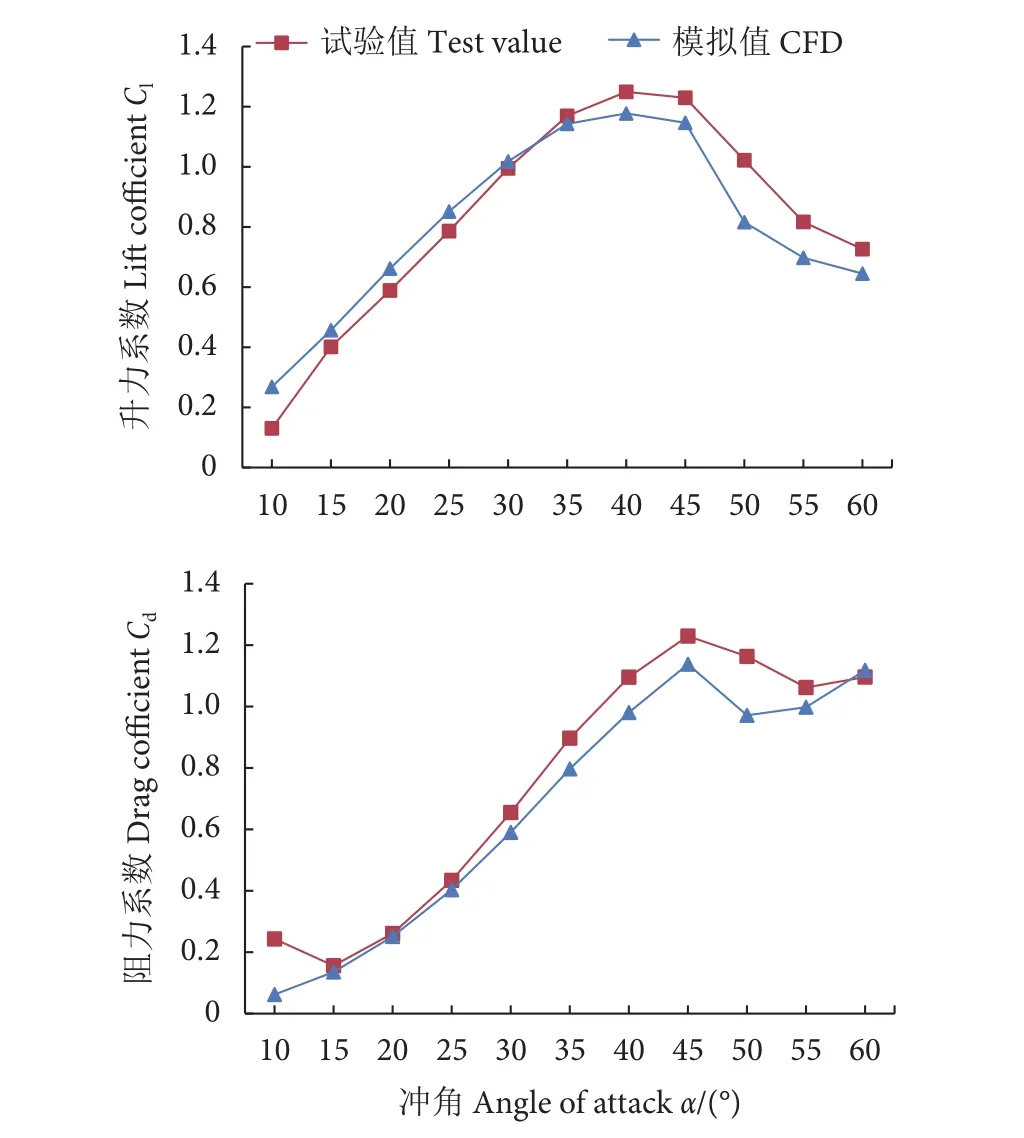
图6 网板模型试验和数值模拟水动力Fig. 6 Comparison of hydrodynamic force of model otter boards between flume tank test and numerical simulation

2.2 尺度比对网板水动力系数的影响

分析1∶2、1∶3和1∶4这3个尺度比的网板水动力模拟结果，不同尺度比网板的水动力系数变化趋势趋于一致。45°冲角之前，阻力系数均随着冲角的增加而增大；在冲角达到45°后，阻力系数出现一个先减小后增大的趋势；升力系数随着冲角的增加先增大后减小。随着模型尺度的增大，网板的升、阻力系数逐渐增大；升、阻力系数在数值上的差异主要出现在冲角30°之后 (图7)。对比分析模拟得到的3种尺度比网板的最大升、阻力系数与尺度比为1∶3的网板 (1#模型网板) 模型试验结果，发现随着模型尺度的增大，最大升力系数与模型试验结果间误差逐渐减小，分别为12.62%(1∶4)、6.03% (1∶3)和 1.13% (1∶2)；最大阻力系数误差也随模型尺度增加而减小，分别为15.07% (1∶4)、7.99% (1∶3)和 1.48% (1∶2) (表 2)。

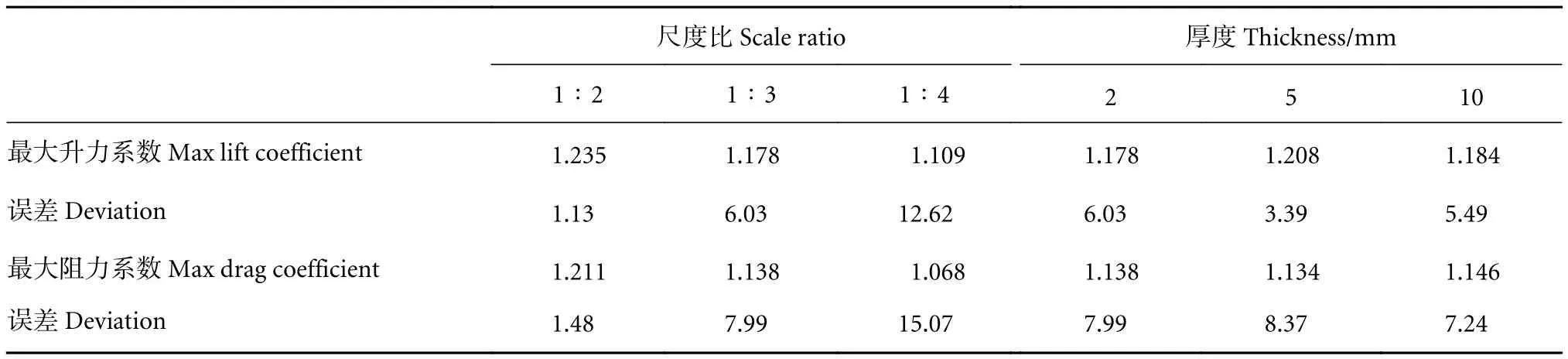
表2 不同尺度比和不同厚度网板水动力系数误差Table 2 Hydraulic coefficient deviation of different scale ratio and thickness of otter board

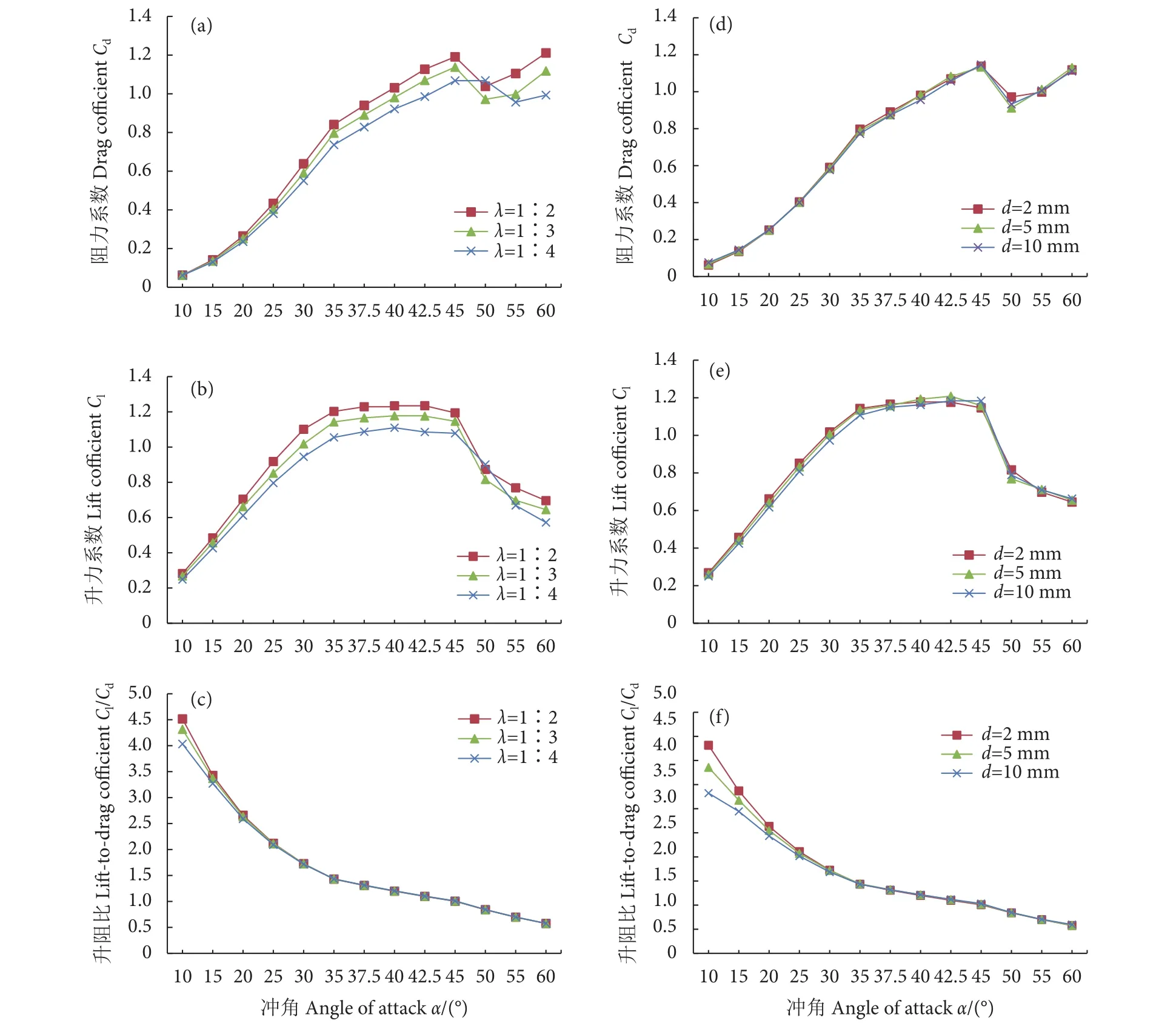
图7 不同尺度比 (左)、厚度 (右) 水动力系数Fig. 7 Hydrodynamic coefficient of different scale ratio (Left) and thickness (Right)

2.3 厚度对网板水动力系数的影响

对比2、5、10 mm这3种网板厚度模型水动力模拟结果，发现不同厚度网板的水动力系数变化趋势趋于一致。45°冲角之前，阻力系数均随着冲角的增加而增大；在冲角达到45°后，阻力系数呈现先减小后增大的趋势；升力系数随着冲角的增加先增大后减小；升阻比随着冲角的增大而减小。不同厚度网板模型之间的水动力系数数值差异较小，不足2.6% (图7)。对比分析模拟得到的3种厚度网板模型的最大升、阻力系数与厚度为2 mm的模型网板 (1#网板) 的模型试验结果，发现5 mm厚的模型最大升力系数的误差最小 (3.39%)，2 mm厚的模型最大升力系数的误差最大 (6.03%)；10 mm厚的模型最大阻力系数的误差最小 (7.24%)，5 mm厚的模型最大阻力系数的误差最大(8.37%) (表2)。

2.4 1∶4尺度比网板流场可视化及对比

流场可视化的基础是雷诺准则，雷诺数是影响流态的一个主要因素。由于网板尺度的不同，为了保证雷诺数一致，需要调整不同尺度网板模型对应的试验流速。因此调整流速后的1∶2、1∶3、1∶4流场图具有相同的流态规律，以1∶4尺度比网板为例。利用CFD后处理软件Fluent，分别对1∶4尺度比V型网板10°～50° 冲角时的周围流场进行可视化处理。如图8和图9所示，随着网板模型尺度的增大，网板表面边界层分离效果逐渐增强，尾流区流场分离涡逐渐增大。随着冲角的增大，网板迎流面的压力由前端不断向后端延伸扩展，压力中心向网板后端偏移。当冲角为50° 时，迎流面压力最大。随着冲角的增大，网板周围的流场速度逐渐增大。流场图中流线表示流场的速度方向，当冲角为10° 时，网板后无分离涡；冲角为20° 时，开始出现分离涡形成的趋势；当冲角达到30° 时，网板后开始出现分离涡，但分离涡较小且不显著；随着冲角的增加，分离涡逐渐增强，并在冲角为50° 时达到最大。不同尺度比网板流场的变化趋势相同。相同工况下，随着尺度的增加，网板迎流面同一位置的压力以及迎流面两侧的升、阻力均逐渐增大，网板迎流面后的分离涡增大。

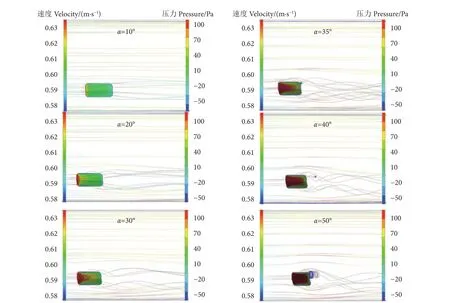
图8 网板在不同冲角下的流场分布Fig. 8 Flow field distribution of otter board at different angles of attack

3 讨论

3.1 模型尺度对网板升、阻力估算的影响

本文采用RANS湍流模型中的K-ε模型进行数值模拟，对比了不同尺度比V型网板的水动力性能。并将尺度比为1∶3的网板水动力模拟结果与模型试验结果进行对照，结果表明升、阻力系数变化趋势吻合较好。模拟值与试验值的数值差异主要出现在30° 冲角前后 (图6)，可从网板周围流场分布方面分析。由于1∶3与1∶4尺度比网板的流态规律相同，从尺度比1∶4的网板流场图 (图8) 中可以观察到，当冲角达到30° 时，网板后部开始出现明显的分离涡。而图9中尺度比为1∶3的网板在冲角为40° 时也出现了分离涡，表明这种分离涡可能导致网板升力减小，进而造成升阻力系数模拟值与试验值数值上的差异。这也是造成网板升力模拟值与模型试验值30° 冲角前后差异的原因[22]。模拟值与试验值阻力系数随着冲角的增大而增大，在冲角45° 后阻力系数出现一个先减小后增大的趋势，这趋势与Xu等[14]发现的阻力系数一直增大的结果有所不同。Su等[5]研究表明，阻力系数先增大后减小，与本研究结果一致。本文的数值模拟结果与模型试验结果中同时存在阻力系数先减小后增大的变化趋势，两种方法结果的相互验证表明，阻力系数先减小后增大的现象可能是正确的 (图6)。网板姿态可能是引起阻力系数先减小后增大的主要原因。本文设定网板的姿态为外倾10° ，而Xu等[14]的网板姿态为直立，无倾斜。网板的外倾可能会导致水流流经网板表面时，网板边界层分离点的移动，并在45° 冲角时产生影响[23]。其次，为了更好地体现底拖网网板的工况环境，本文在数值模拟中将网板设置在数值水槽的底部，以模拟底层水流对网板的作用；而模型试验由于试验条件的限制，网板被设置在水流的中上层。根据Park等[24-25]的研究结果，不同水层水流流经网板表面的接触位置不同，会导致网板水动力测量数值的不同。

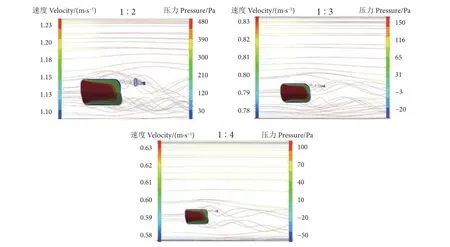
图9 不同尺度比网板在40°冲角下的流场对比Fig. 9 Flow field comparison of otter board with different scales at 40° angle of attack

不同尺度比网板模型的水动力模拟结果显示，升、阻力变化趋势趋于一致，但数值差异较大(图7)。尺度效应是产生结果差异的主要原因。以本文的3种尺度比为例，网板尺度从1∶2到1∶4，两者最大升力系数相差11.49%，最大阻力系数相差13.59%。不同厚度网板模型的水动力模拟结果，升、阻力变化趋势趋于一致且数值差异较小(图7)。3种厚度的最大升、阻力系数的最大偏差分别为2.64%和1.13%。因此，在以模型尺度为基础的网板水动力预测估算中，不能忽视尺度效应对网板水动力预测上的影响。

3.2 模型尺度对网板流场的影响

流场可视化的方法主要有线条法、氢气泡法和Fluent模拟法[22]。流场研究的主要关注点为流场分离区和分离涡，分离区主要为网板表面边界层的分离情况，分离涡主要为网板的尾流区涡以及特征部位如尖端的涡[21]。探究网板周围流场流态对于分析网板水动力变化规律至关重要，也是解释网板水动力机理的有力依据。Shen等[26]采用氢气泡法对高升力网板流场进行了探究，认为翼尖涡会对网板的升力产生影响。Xu等[14]采用Fluent对V型网板的周围流场进行了可视化，认为翼尖涡增大了网板的升力，当翼尖涡消失时网板升力开始减小。

本文采用Fluent的方法对相同工况下1∶2、1∶3、1∶4这3种尺度比的V型网板流场进行了可视化处理，发现随着网板尺度的增大，网板表面流线分离程度越显著，这揭示了微观尺度下网板表面边界层分离点的位置变化。对网板水动力影响最大的一部分流场区域是网板尾流区的分离涡。随着网板尺度的增大，网板尾流区的分离涡也逐渐增大，并且分离涡与网板之间的距离逐渐增加。流场中产生的分离涡会引起网板升、阻力的改变，影响效果与分离涡的大小以及分离涡与网板的相对位置密切相关。例如，本文中随着尺度的增大，分离涡的大小也逐渐增大，但大尺度比网板的升、阻力系数却高于小尺度比网板，这说明分离涡与网板之间的相对位置可能是影响升、阻力变化的关键因素。

3.3 模拟条件对网板升阻力估算的影响

通过模型试验验证数值模拟结果发现，数值模拟与模型试验在网板水动力的估算数值上存在一定差别。为了提高网板数值模拟预测的准确性，探究数值模拟过程中可能产生的所有误差是必要的。整个数值模拟过程中可能出现的误差主要有3种，分别为建模误差、离散误差和计算误差[27-28]。其中建模误差为主要误差原因，离散误差和计算误差对结果偏差的影响程度有限。建模误差主要受到模型物理参数及初始条件的影响，即尺度效应的影响。离散误差主要受到模拟时网格的密度分布和边界条件的影响[29-30]。Xu等[14]对比了4种不同网格密度下网板升、阻力的差异，结果显示网格数量从9.3×105增至2.3×106，网板的升、阻力误差分别降低了0.6%和0.8%。在后续研究中应以网板水动力系数和网格数量的收敛性分析作为研究基础。计算误差包括舍入误差和迭代误差，当离散方程不完全满足绝对收敛，而是在满足设定的一定条件 (如离散方程的余量小于一定值) 下终止迭代，这时得到的数值解与理论上的精确解之间出现的偏差即为计算误差[31]。

本文主要通过对比分析不同尺度比和不同厚度的网板模型的水动力系数差异，研究和分析了建模误差即尺度效应对网板水动力的影响，结果表明尺度比对网板水动力系数的预测结果存在一定程度的影响。以最大升力系数为例，1∶4尺度比下最大升力系数与模型试验结果的偏差达到了12.62%；1∶2尺度比下最大升力系数与模型试验结果的偏差为1.13%。网板模型厚度对水动力的预测结果影响较小。以最大升力系数为例，2 mm厚度的网板最大升力系数与模型试验结果的偏差达6.03%；10 mm厚度的网板达5.49%。为提高数值模拟中网板水动力预测的准确性，对离散误差即模拟过程中不同模拟条件设定产生的误差和计算误差进行系统试验研究是必要的。针对模拟过程中的离散误差可以设定不同的网格划分方法、网格数量、网板表面边界层的厚度、不同的求解器以及调整网板在水槽中的相对位置等模拟条件，对比计算得到的网板水动力结果，分析得到预测网板水动力模拟中最佳模拟条件的设定。计算误差可以通过比对同一网格设定条件下的多次反复计算来提高水动力预测的准确性。