基于双重残差注意力网络的图像超分辨率重构方法*

张美燕，吴 岩，蔡文郁*

(1.浙江水利水电学院电气工程学院，浙江 杭州 310018；2.杭州电子科技大学电子信息学院，浙江 杭州 310018)

图像超分辨率重构(Image Super-Resolution Reconstruction，SR)是计算机视觉和图像处理领域的研究热点，尤其是单幅图像超分辨率重构(Single-Image Super-Resolution Reconstruction，SISR)在近几年得到了越来越多的关注。 SISR 是指从一个低分辨率(Low Resolution，LR)图像恢复出一个高分辨率(High Resolution，HR)图像的过程[1]。 图像超分辨率重构具有广泛的现实应用，例如视频监控、遥感、医学成像，以及作为图像分类、识别、去噪和检测的预处理[2-8]。 图像超分辨率重构是一个具有挑战性以及固有不适定性的问题，因为总是存在多个HR图像对应单个LR 图像[9]。 目前主流的图像超分辨率重构方法分为以下三类:基于插值的SR 法、基于重构的SR 法和基于学习的SR 法。 基于插值的SR方法非常简单，直接利用自然图像的先验知识，因此不能提供超分辨重构所需的额外信息。 基于插值的SR 方法主要包括最近邻插值[10]、双线性插值[11]和双三次插值[12]等。 基于重构的SR 方法引入某些先验知识和约束，包括迭代反投影方法(Iterative Back-Projection，IBP)[13]、凸集投影法(Projection Onto Convex Sets，POCS)[14]、最大后验(Maximum A Posteriori，MAP)概率法[15]等。 这类方法多依赖一组高度相关的LR 图像序列进行重构，但是重构模型的参数很难精确估计，如果使用场景无法提供足够信息时，提高图像分辨率变得非常困难。

Dong 等人[16]首次将卷积神经网络运用到图像超分辨问题中，并取得了良好的重构效果，越来越多的研究将卷积神经网络应用于SISR 领域。 Kim 等人[17]提出了一种超深的网络架构VDSR，通过对残差图像学习获得较好的图像超分辨率重构效果。 为了提升SR 的速度，Dong 等人[18]又提出了网络架构FSRCNN，将低分辨率图像输入卷积神经网络进行学习，在末端利用反卷积进行上采样降低模型计算量。 2016 年Shi 等人[19]提出了网络架构ESPCN，可以在低分辨率空间进行学习，通过亚像素卷积的方式对图像进行上采样。 2017 年，Zhu 等人[20]提出了CycleGAN(Cycle-Generative Adversarial Network)用于图像转换，将双重学习结构应用于训练未配对的数据，并提出了一种循环一致性损失来避免GAN 方法[21]的模态崩溃问题，并帮助最小化分布散度。 同年，Lim 等人[22]认为SRGAN 生成器中残差网络结构中的BN 层会减小网络范围的灵活性，他们对残差网络进行简化之后，提出了非常宽的网络架构EDSR。 Zhang 等人[23]认为以前的SR 方法对每个信道的特征都进行了平等学习，缺乏对不同类型信息(如低频和高频信息)学习的灵活性并且耗费过多的计算资源，因此他们在残差网络中加入了注意力机制，提出的RCAN 网络建立长跳连接和短跳连接用于忽略中间丰富的低频信息。

新型的图像超分辨率重构算法多以卷积神经网络、残差网络[24]、亚像素卷积层[18]为基础，通过修改网络结构提高算法速度和精度。 图像超分辨率重构作为低级图像处理任务，要求尽可能保留图像的底层信息。 现有算法存在两个主要问题:一是学习从LR 图像到HR 图像的映射函数通常是一个不适定问题，因为存在无数的HR 图像可降采样到同一LR 图像，所以可能存在的函数空间非常大，很难找到一个很好的解决方案；二是现有算法为了提升网络的特征提取能力往往采用更深更大的网络架构，导致网络参数量巨大，因此消耗了大量计算资源；而且超分辨率重构后得到的图像过于平滑，缺少细节纹理信息，不够逼真。 针对以上问题，提出了一种基于双回归网络的图像超分辨率重构算法，采用双重残差注意力网络(Dual Residual Attention Network，DRAN)实现泛化界最小化，实验结果表明本文方法能够获得更好的主观视觉评价和客观量化评价。

1 基于双回归网络的超分辨率重构算法

基于双回归网络，提出了双重残差注意力网络的图像重构方法，通过引入双回归方案提出了对LR数据进行附加约束以减少可能的函数空间，解决了现有的SR 方法在学习从LR 图像到HR 图像映射函数的不适定问题。 双重残差注意力网络主要由原始网络和回归网络组成，原始网络负责学习LR 图像到HR 图像的重构，对偶回归网络负责估计降采样核和重构LR 图像。 本文主要创新点如下:提出了基于双回归网络的双重残差注意力网络(Dual Residual Attention Network，DRAN)的图像超分辨率重构方法(DRAN-SR)，获取了更好的峰值信噪比和结构相似性。

本文研究的DRAN-SR 模型结构如图1 所示，其中x代表LR 图像，y代表HR 图像，DRAN-SR 同时学习原始映射P重构HR 图像和对偶映射D重构LR图像。 原始重构任务可以表示为:学习函数P:x→y，使得预测的P(x)与其对应的HR 图像y相似；对偶回归任务可以表示为:学习函数D:y→x，使得预测的D(x)与其对应的LR 图像x相似。 原始重构任务和对偶回归任务可以形成一个封闭的循环，并提供信息监督来训练模型P和D。 理论上如果P(x)是正确的HR 图像，那么下采样图像D(P(x))应该非常接近输入的LR 图像x。 在此约束条件下，可以减少可能的映射函数空间，并使它更容易学习到一个更好的映射来重构HR 图像。 下文将对各个具体模块进行详细介绍。

图1 DRAN-SR 网络架构

1.1 原始网络

原始网络的任务是将LR 图像重构为HR 图像，原始网络包括log2(s)个重构块，其中s表示超分辨率的倍率。 本文选择基于注意力机制的多级残差网络(Multi-Residual Attention Network，MRAN)作为原始网络的重构块，通过引入空间注意力模块和通道注意力模块改进残差网络，该网络提高了对重构关键信息的提取能力。 重构块MRAN 主要包括浅层特征提取模块、残差集合模块和上采样重构模块。每个残差集合包含8 个残差组(Residual Group，RG)，RG 网络结构如图2 所示。 每个残差组由4 个残差块(Residual Block)、1 个聚合模块、1 个通道注意力模块以及1 个卷积层组成。 本文的残差块采用了EDSR 网络的RB 结构，并在末端添加空间注意力模块，从而提高网络的特征提取能力。

图2 MRAN 的残差组RG 结构

1.2 回归网络

回归网络的任务是将重构得到的HR 图像降采样为LR 图像。 理想情况下，如果从LR→HR 的映射最优，则超分辨重构所得HR 图像可以向下采样以获得相同的输入LR 图像。 基于这样的约束，本文估计底层的下采样核，从而减少可能函数的空间。对偶回归映射是学习潜在的退化方法，相较于学习从LR 到HR 的重构简单得多。 所以，本文算法只设计了两个卷积层和一个LeakyReLU 激活层作为回归块，因此计算成本比重构块更低，但在实际中有良好的效果。 回归块的模型结构如图3 所示。

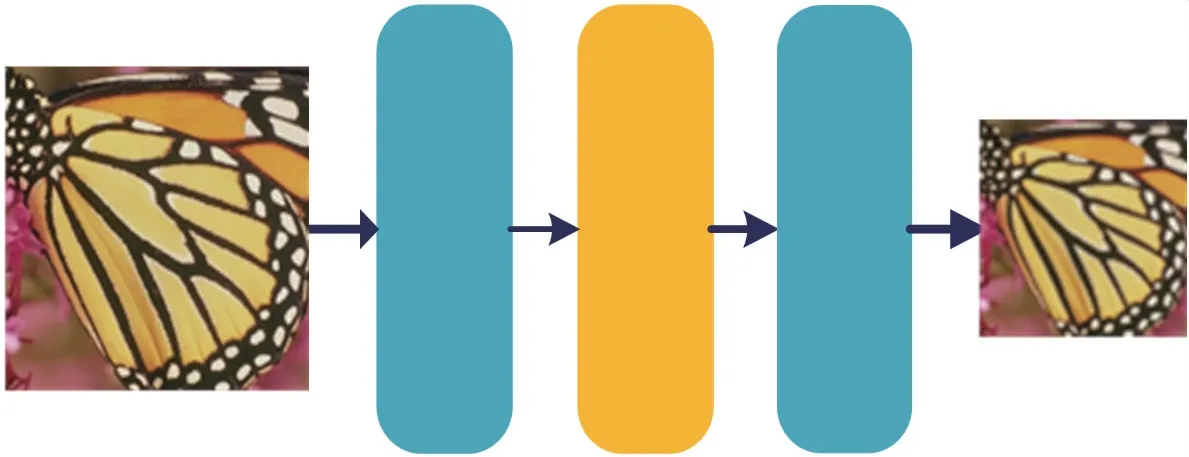
图3 回归块模型结构

1.3 损失函数设计

为了兼顾原始回归网络和对偶回归网络对于优化结果的权重，本文设计的DRAN-SR 算法的损失函数主要由两部分组成，如式(1)所示:

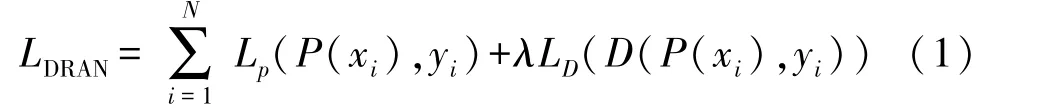
式中:N表示成对的样本Sp={(xi，yi)}i=1，xi，yi表示成对数据集中的一对低分辨率和高分辨率图像，P(xi)表示通过原始网络的重构得到HR 图像，D(P(xi))表示由回归网络对重构HR 图像降采样得到的LR 图像，λ表示双回归损失函数的权重系数，Lp和LD分别表示原始回归任务和对偶回归任务的损失函数(即L1损失函数)。L1损失函数也称为最小化绝对误差(Least Absolute Error，LAE)，目标是最小化真实值yi和预测值f(xi)之间的差值和DL1的绝对值，如式(2)所示:

式中:DL1表示平均绝对误差(MAE)，L1损失函数表示为minDL1。 下文讨论如何确定式(1)中的权重系数λ，表1 所示的为通过实验测试不同值对结果的影响，λ的值从0.001 增加到10，λ值越大说明对偶回归模块在损失函数中所占比重越大，即约束效果越强。

表1 权重系数与PSNR 的影响

从表1 中可以看出，λ过小时，回归网络的约束力也比较小，无法提供有效的监督，导致图像超分辨率重构的结果一般；当λ逐渐增大时，回归网络在损失函数所占的比重越来越大，约束力越来越强，导致双回归网络的原始模块无法很好地学习从LR 图像到HR 图像的重构效果。 本文最终选定λ取值0.1，原始网络和回归网络在损失函数中所占比重达到较好的平衡状态。

1.4 理论分析

模型测试数据样本所表现的误差期望称为“泛化误差”(Generalization Error)，泛化误差常用来衡量一个模型对于未知数据的泛化能力。 本文利用泛化误差来验证所提出的回归方案的有效性，并通过拉德马赫复杂度[25]来获得本文所提出双回归模型的泛化界。

本文将双重残差注意力网络的泛化误差定义如下:

式中:P表示原始任务，D表示回归任务，在实际中双回归网络的目标是双向优化任务，对于N个样本的经验损失定义如下:

按照文献[26]定义了对偶学习的函数空间Hdual∈P×D，拉德马赫复杂度可以衡量函数空间的复杂度，也就是说它可以得出原始网络和回归网络的丰富性，复杂度越高的函数簇对应的拉德马赫值越高。 对于一个基本分布S，Z={z1，z2，…，zN}是样本集合，其中zi={xi，yi}，则双回归网络在集合Z上的经验拉德马赫复杂度＾Rz(P，D)为:

泛化误差上界是指泛化误差允许的最大值，泛化误差是指模型由训练集泛化至测试集的过程中产生的误差，一般用训练集外的误差，即整个输入空间上的误差期望减去训练误差。 本文分析了该对偶回归方案的泛化界，从有限函数空间的简单情况开始，将其推广到一个具有无限函数空间的更广泛情况。令LP[P(x)，y]+λLD{D[P(x)，x]}是从x×y映射到[0，C]的一簇函数，假设函数空间Hdual是有限的，则存在一个满足0≤η≤1 的η，至少以概率1-η，使不等式(7)成立:

因此，在相同的训练集样本数量条件下，本文所提出的DRAN-SR 算法具有更小的泛化界，在未知数据中取得更好的图像超分辨率重构效果。

2 实验结果与分析

本文采用DIV2K 测试数据集作为数据源，该数据集包含1 000 张2 K 高清图像。 测试过程中利用数据集中成对的高分辨率原图与对应2、3、4、8 倍降采样低分辨率图片进行模型训练，并采用了五个基准测试集Set5、Set14、BSD100、Urban100 和Manga109 对所提出的DRAN-SR 算法进行测试验证。

实验场景设置如下:DRAN-SR 使用RGB 三通道图像进行训练，在输入前对图像做归一化处理，每一批输入是16 幅尺寸为48×48 的图像，这些小的图像块都从数据集原图中随机截取得到，提高了数据丰富性。 训练过程使用L1 损失函数和Adam 优化器，其中β1=0.9，β2=0.999，ε=10-8，学习率初始化设置为10-4。 在迭代过程中通过余弦退火下降方式逐渐降到10-7，双回归损失函数的权重系数λ设为0.1。 实验用到的主要参数如表2 所示。

表2 实验参数设置

本文设置原始回归网络的每个基础重构块MRAN 包含8 个残差组RG，则对应4 倍的超分辨率原始网络包括2 个基础重构块，共有16 个残差组RG；8 倍的超分辨率原始网络包括3 个基础重构块，共有24 个残差组RG。 本文对DRAN-SR 算法与其他网络在Set5 数据集上进行4 倍超分辨率重构，网络性能与参数量之间的对比关系如图4 所示。

图4 不同模型参数量与重构性能对比

图4 中横坐标表示模型的参数量(百万级别)，纵坐标表示峰值信噪比(Peak Signal to Noise Ratio，PSNR)性能指标。 从图中可以看出，在Set5 测试集中DRAN 的PSNR 明显优于传统的插值法、SRCN 及VDSR 算法，与参数量庞大的EDSR 相比也有其优势。

为了验证双回归超分辨率重构的有效性，本文进行了四倍超分辨率重构的消融实验(Ablation Experiment)，实验结果如表3 所示。 从表3 中可以看出DRAN-SR 与基线相比，双回归模型在各个数据集上都有更好的性能。

表3 双回归方法消融实验(SR×4)

通过引入一个附加的约束条件来减少映射函数的空间，对偶回归方案可以改善HR 图像的重构效果。 表4 给出了DRAN-SR 与其他方法在各个基准数据集上2、3、4、8 倍重构后图像的PSNR 和结构相似性(Structural Similarity，SSIM)，最好结果和次好结果分别使用黑体和下划线标记。

表4 实验结果对比

从表4 中可以发现，DRAN-SR 算法的结果明显优于EDSR-SR、VDSR-SR、SRCNN-SR、Bicubic-SR 等算法。 在重构倍率较小的情况下，DRAN-SR 在小部分测试集中的结果略差于EDSR。 但在重构倍率较高的情况下，DRAN-SR 的重构效果明显优于拥有更大参数量的EDSR-SR。 因此，由于强大的特征提取能力和更好的学习能力，DRAN-SR 在不增加额外参数的前提下，在重构倍率较高的图像超分辨率重构中取得更好的结果。

图5 显示了不同图像超分辨重构算法在各个基准测试集中得到的测试图像，可以发现DRAN-SR得到的重构结果细节更丰富，边缘纹理更加清晰，从视觉上能给人带来更好的主观体验。

图5 基准测试集测试结果

3 总结

本文引入对偶双回归网络架构，将基于注意力机制的多级残差网络作为原始网络的基础重构块，提出了一种基于双重残差注意力网络结构的图像超分辨重构方法。 回归网络结构模型通过对LR 数据增加额外约束减少可能的映射空间，提高HR 图像的重构质量，多级残差注意力网络通过强大的特征提取能力和更高的特征利用率，使得重构的HR 图像拥有更多的细节纹理。 基于标准测试集的实验结果验证了本文算法相较于以前的图像超分辨重构方法，在主观视觉评价和客观量化评价上都取得了明显的性能提升。