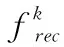拟凸优化问题中常值步长准则下次梯度算法的收敛性

赵婷婷

西安交通工程学院公共课部 陕西西安 710300

1 概述

数学优化是很多学科的研究基础，凸优化是数学优化的一个重要的分支。在一些实际问题的研究，尤其是在经济管理等领域，“凸”的要求过于苛刻，见文献[11-12]。而“拟凸”不仅有“凸”的优势(有全局最小值)，又能刻画很多实际研究中的问题，见文献[13]。

拟凸优化问题在很多领域都有重要的应用，尤其在经济学、工程学和管理学中，见文献[13]。用次梯度法去解决拟凸问题的研究有限。Kiwil给出了在递减步长准则下目标函数为上半连续时拟凸优化算法的收敛性及收敛速度，见文献[16]。Gasimov改进了对偶次梯度算法，见文献[17]。胡耀华等给出了一个不精确的次梯度算法解决拟凸优化问题，并证明了其收敛性，见文献[5]。本文主要研究的是以下拟凸优化问题:

其中

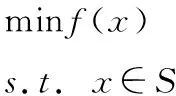
f

：

R

→

R

是一个拟凸函数，约束集

S

是非空闭凸集。我们将最优解集和最优解分别记为

S

和

f

，并假设最优解集

S

是非空的和紧的。

次梯度算法是解决拟凸优化问题的一种常用的方法，但算法的收敛理论，尤其是算法的收敛速度理论与算法的步长准则的选取有关系。本文首先给出了一个次梯度算法的统一框架；其次给出拟凸优化中次梯度算法在常值步长准则下的收敛性；最后进行数值实验，对算法的收敛性进行了数值分析。

2 相关符号

对问题(1)，我们首先给出以下的相关符号：

f

和

S

分别表示最优值和最优点集，即有，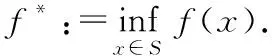

S

：={

x

|

f

(

x

)=

f

}.记

x

在

S

上的投影和

x

到

S

距离分别为：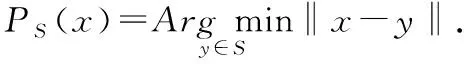

设

a

∈

R

，记函数

f

的水平集L(

α

)={

x

∈

R

|

f

(

x

)≤

α

}.

以下是拟凸的定义：

定义1：函数

f

：

R

→

R

称为拟凸函数，如果满足

f

((1-

α

)

x

+

αy

)≤max{

f

(

x

)，

f

(

y

)}，∀

x

，

y

∈

R

，∀

α

∈[0，1]

.

次微分的定义对于解决拟凸优化问题相当重要。凸分析中常用的次梯度为Fenchel-Moreau(FM)次微分，详见文献[15]，函数

f

在

x

处的FM次微分定义为：∂

f

(

x

)={

g

∈

R

|〈

g

，

y

-

x

〉≤

f

(

y

)-

f

(

x

)，∀

y

∈

R

}.次梯度法的主要思想是将梯度法中的梯度用任意的次梯度代替。因为拟凸函数的次FM微分可能会是空集(

y

=

x

在

x

=0时)，为了拟凸函数次微分的计算，1973年Greenberg-Pierskalla最先提出了GP次微分，函数

f

在

x

处的GP次微分定义为(详见文献[3])：∂

f

(

x

)={

g

∈

R

|〈

g

，

y

-

x

〉≥0⟹

f

(

y

)≥

f

(

x

)，∀

y

∈

R

}.

除此之外，拟凸函数的次微分的定义还有其他的形式，见文献[3，5，18，19]。但是，GP次微分不是闭集，为了克服这一点，Kiwiel和胡耀华引入了一种拟次微分，其定义如下(本文使用的就是这种次微分)：

定义2：

f

：

R

→

R

是一个拟凸函数，且

ε

>0，则函数

f

在

x

∈

R

处的拟次微分及

ε

-拟次微分定义分别如下：∂

f

(

x

)={

g

∈

R

|〈

g

，

y

-

x

〉≤0，∀

y

∈lev<()

f

}，

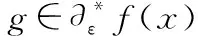
3 算法及收敛性分析

在这一部分，首先，我们参考凸优化中的次梯度算法，给出了拟凸优化中的次梯度算法，在算法中选取的步长准则为常值步长准则；其次，对算法的收敛性给出了分析。下面是拟凸优化中的次梯度算法。

算法1：

步1给出初值

x

∈

R

，

k

=1；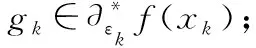

步3令

z

=

x

-

v

g

/

‖

g

‖，

x

+1=

P

(

z

)，

k

=

k

+1，转步2。算法的收敛性。对于凸优化和拟凸优化来说，次梯度迭代的基本不等式是分析算法收敛性的重要工具。YU提出了对多种次梯度算法收敛的统一框架，详见文献[10]。在实际应用中，由于误差的存在，胡耀华提出了非精确的次梯度算法。本文讨论了次梯度算法产生的点列{

x

}满足一个非精确的基本不等式(即为引理1)，且讨论了在次不等式下算法的收敛性。引理1 设{

x

}为算法1产生的点列，对于每个

x

∈

S

及

k

∈{

i

∈

N

：

f

(

x

)>

f

+

ε

}，有: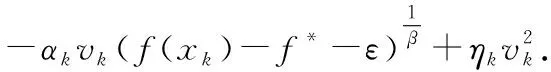

(1)

{

α

}和{

η

}是两个正数列，满足:

(2)

其中固定

ε

≥0，

p

>0。

从引理中的式(1)可以看出，算法的迭代点到最优解之间的距离是在不断接近的。式(2)是对参数的假设。为了对算法收敛性的分析，下面给出算法收敛性分析中会用到的一个重要引理，详见文献[20]中的Lemma2.1。

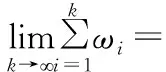
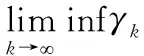
下面对常值步长准则下算法的收敛性给出分析。

定理1 设{

x

}为算法1采用常值步长

α

≡

α

产生的点列，且{

x

}满足引理1，则有: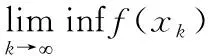

证明：在算法1中，我们不妨假设有有限个

k

满足

f

(

x

)≤

f

+

ε

，否则定理1一定成立。即，存在

K

∈

N

，对任意

k

≥

K

，都有:

f

(

x

)>

f

+

ε

.令

x

∈

S

，则由引理1、式(1)可得，对任意

k

≥

K

，都有: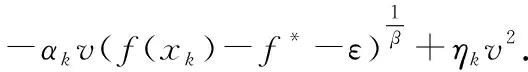

将上式从

k

=

K

，

K

+1，…，

n

进行累加，可得: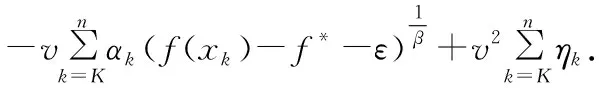

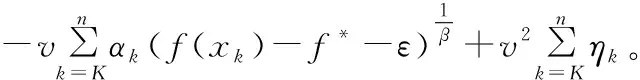
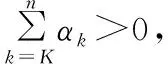
上式结合引理2可得:

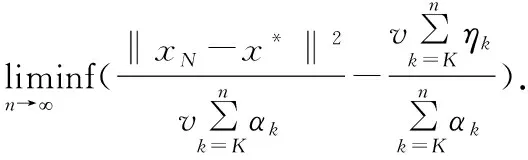
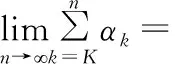
即可得此定理成立。

4 数值实验

在这一节，我们将以数值实验的形式来对算法1在常值步长准则下的收敛性进行分析，编程软件为Matlab 2016a。所用的数值算例均来源于文献[21]。

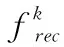
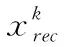
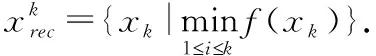
例1 求解

其中

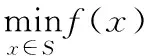
S

=[-1，1]，

f

：

R

→

R

定义为对∀

x

∈

S

，

容易验证，

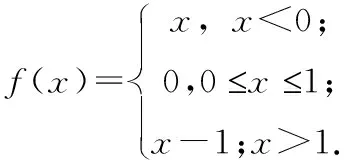
f

(

x

)为拟凸函数，且

f

=-1。

例2 求解

其中

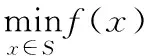
S

=[-1，2]，

f

：

R

→

R

定义为对∀

x

∈

S

，

容易验证，

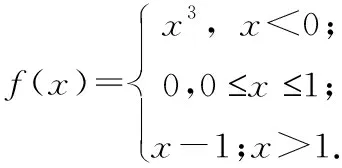
f

(

x

)为拟凸函数，且

f

=-1。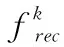

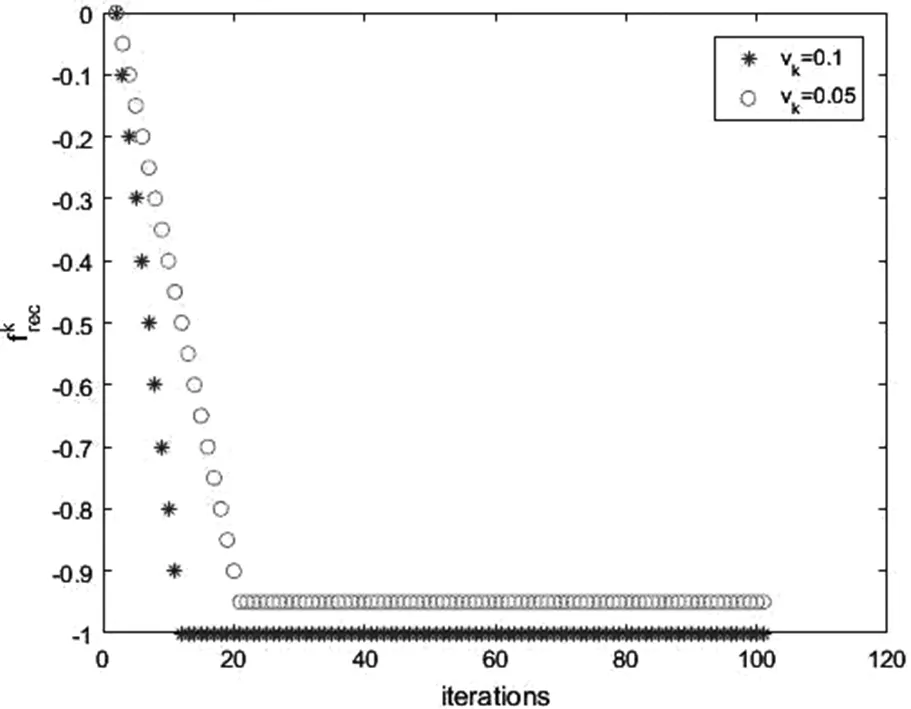
图1

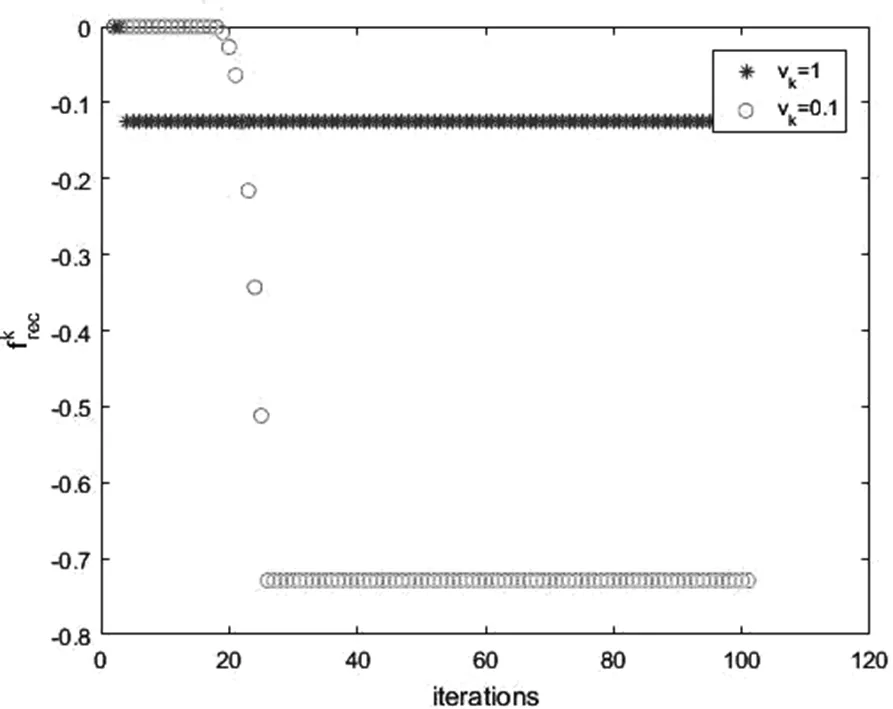
图2

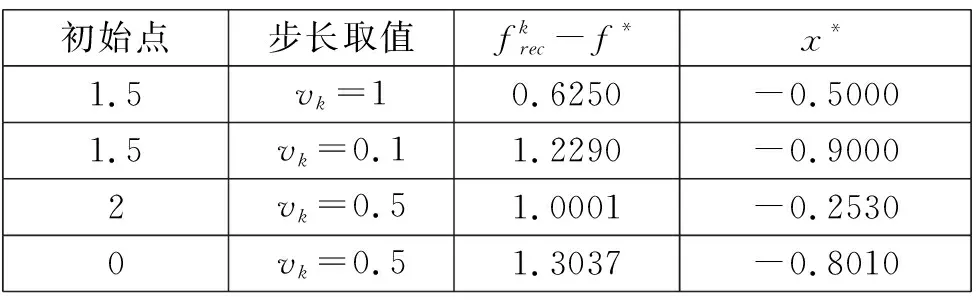
表1

结语