交叉跑道进离场航空器安全间隔研究

胡明华，王旗，王春政，赵征

（南京航空航天大学民航学院，南京 211106）

0 引言

随着机场跑道运行日益繁忙，导致航班大量延误，需要尽可能增加跑道数量来提高机场的通行能力。目前国内机场跑道建设的数量不断增加，使得机场跑道的运行安全环境相对复杂，亟需解决机场跑道运行安全间隔问题。国内对平行跑道安全运行的研究相对较多，而对交叉跑道运行安全的研究较少，鲜见有关于交叉跑道上进近航空器又复飞导致其与离场航空器产生安全问题的相关研究。而对交叉跑道运行安全问题的研究将会改变离场航空器的放行间隔。

交叉跑道在国外建设比较多，其主要参考FAA发布的ORDER JO7110.65X，其中规定“假设跑道的中心线延长穿过汇聚跑道或汇聚跑道延长的中心线，并且距离两个离场端不大于1 n mile”。针对交叉跑道，也规定了如果非交叉跑道偏离15°及以上，且跑道边缘不接触，即为非交叉分散跑道。欧美发达国家已经开始建造多条跑道，国外对多跑道运行安全问题进行了大量的理论研究，例如，1995年，R.Slattery等通过空中交通管制对平行跑道的精密进近进行了研究。较早的理论研究可以追溯到20世纪60年代，其中英国的P.G.Reich提出了Reich碰 撞风险模型，该 模型就是将长方体模板的长、宽、高分别表示为两架飞机的机身长度、翼展和机身高度，飞机质点向碰撞盒穿过，当质点进入至位于碰撞盒航空器的内层或表面时，意味着两架飞机发生了碰撞；K.Pang等以国际民航组织规定的航速分类为依据，对平行跑道的安全间距进行了研究，旨在为适用于不同航速组合的平行跑道配置提供更为合理的规划，并建立了改进的仿真模型，当由不同机型组成时，重点研究了接近速度差异最大的A-E机型组合，在A-E机型组合情况下，跑道间距10.35 m时碰撞风险相对较高；N.M.Guerreiro等通过模拟实验，对近距平行跑道（CSPR）运行概念进行可行性分析，通过尾流特征数据证明尾流对飞机安全运行因素有重要影响，并表明尾流的传播特性可以被用作评估后机跟随前机的间隔时间和距离；D.C.Burnham等提出了近距平行跑道平行仪表进近尾流湍流安全间隔的建立方法，安全标准基于外界天气的侧风影响，通过尾流模型对芝加哥和达拉斯国际机场中航空器产生的尾流移动影响范围进行了研究，对尾流纵向间隔和侧向间隔的权衡进行了评估。

国内，Liu Fei等提出飞行轨迹的仿真计算方法、碰撞风险计算方法以及尾涡遭遇风险计算方法，通过对不同情况下的飞行轨迹进行仿真计算，发现碰撞冲突和尾流遭遇的概率均低于现行的运行规则；张兆宁等提出了基于航空器碰撞发生概率来确定侧向跑道上航空器进场保护区的方法，通过建立碰撞风险模型来确定航空器在不同位置下的碰撞概率，并通过拟合方法确定安全保护区范围；岳睿媛等提出基于改进Event模型的航路飞行过程垂直碰撞风险评估方法来改进前后碰撞盒的面积大小比值，通过改进方法计算航空器在航路中垂直碰撞风险是原长方体Event模型碰撞风险模型的13%左右；何昕等对侧风影响下的尾流间隔进行优化，分析尾流消散及运动情况，并建立尾流间隔模型，以虹桥机场为例，模拟仿真出在侧风大于2.5 m/s时，对起飞尾流间隔进行缩减，并验证了计算结果的安全性；王莉莉等提出在近距平行跑道一起一降模式中研究ADW（到达与离场）窗，并通过碰撞风险模型来求解大兴机场近距平行跑道ADW窗下边界。

上述研究的碰撞风险模型和尾流模型大多是针对平行跑道的，对交叉跑道的研究相对较少，而且在交叉跑道求解ADW窗下边界对尾流因素方面的考虑欠缺，导致结果偏大而影响运行效率。针对上述问题，本文首先通过建立碰撞风险模型计算进场航空器至跑道入口端的距离；其次建立两机航迹交叉时的尾流间隔模型，以验证进场航空器至跑道入口端的不同距离下，离场航空器是否对进场航空器有影响，并找出安全距离的边界；然后将碰撞风险模型计算出的距离与尾流间隔模型计算出的距离作比较取最大值即可；最后以大兴机场为例，通过两个模型结果比较而计算出最终安全间隔的最小边界。

1 交叉跑道现有规章运行模式与问题

FAA出台的文件7110.65X中规定了非交叉聚汇跑道运行和非交叉分散跑道运行的规则。当飞行路径交叉时，为使用非交叉跑道的航空器与离场航空器之间配备间隔，确保离场航空器没有开始起飞滑跑，直到有下列情况之一存在时：

（1）前机已经离场并越过了离场跑道，或者正在转弯以避让任何冲突；

（2）前方进场的飞机已经完成着陆滑跑，将在预定交叉路口外等待，已经通过预定交叉路口，或者已经越过起飞跑道。

FAA的规定只是解决了进场航空器着陆，同时起飞离场航空器从一条跑道起飞。但是规定中没有说明当进场航空器出现转弯复飞时，与起飞航空器可能出现航迹交叉的情况，这时就有可能发生危险，可能发生碰撞和起飞航空器爬升过程产生的尾流对复飞航空器产生尾流影响。

在大兴机场和天府国际机场跑道运行中，复飞发生的情况为千分之一，对于管制员来说，复飞情况发生的概率较低，比较难以预测，很难准确把握离场航空器起飞的时机，因此对于研究ADW窗下边界并优化下边界的问题尤为重要。进场航空器最小安全间隔如图1所示。

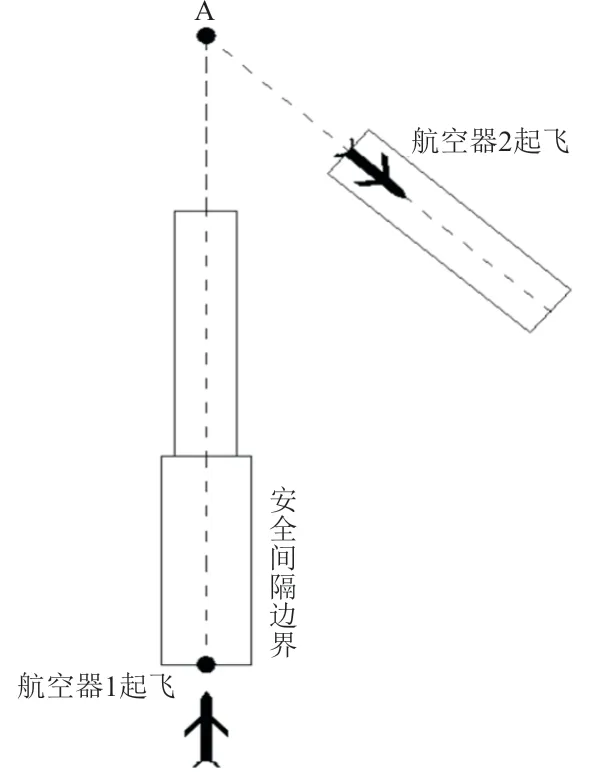
图1 进场航空器最小安全间隔Fig.1 Minimum safety interval for approaching aircraft

2 基于位置误差的航空器碰撞风险模型建立

本文交叉跑道碰撞风险是取纵向和侧向两个方向为主进行研究，且只考虑两机飞行位置误差因素作为碰撞的主要因素，垂直方向碰撞概率取值为1。定义进场航空器为后机1，起飞离场航空器为前机2。以进场跑道中心线为两架航空器的纵向距离，垂直于跑道中心线的水平方向为两架航空器的侧向距离。考虑交叉跑道运行规则特点，根据文献［14］，建立交叉跑道的复飞和离场碰撞风险模型，该过程如图2所示。

图2 复飞与离场航空器飞行过程Fig.2 The flight process of the go-around and departure aircraft

2.1 复飞与离场航空器运动学模型

降落航空器1进近复飞和起飞航空器2离场的全部飞行过程：首先降落航空器在进场过程中降落失败而导致在复飞点处进行复飞，而离场航空器同时起飞直线爬升，降落航空器复飞过程会到达某一点开始转弯复飞，再加速爬升与航空器2起飞爬升过程会有航迹交叉，直至航空器1爬升至V点，航空器2爬升至V点分散式结束。规定进场航空器进场方向为北。其符号含义如表1所示。

表1 符号说明Table 1 Symbol Description

（1）T时段

当进场航空器北向复飞时，还未到达复飞点之前第一阶段，飞机开始减速下降，该时段为T时段，其中T∈[0，t]，t∈T。

两架飞机的纵向距离表达式为

两架飞机的侧向距离表达式为

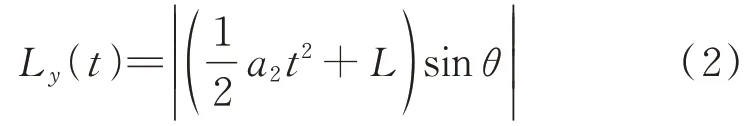
（2）T时段

当进场航空器北向复飞时，还未到达复飞点之前第二阶段，飞机开始匀速下降，该时段为T时段，其中T∈(t，t+t]，t∈T。

两架飞机的纵向距离表达式为

两架飞机的侧向距离表达式为

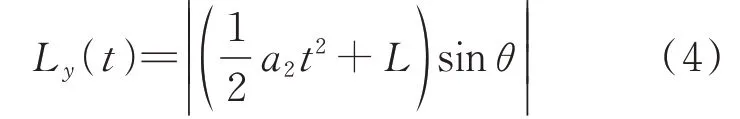
（3）T时段

当进场航空器北向复飞时，到达复飞点，但还未到达起飞爬升点之前，飞机保持匀速平飞，该时段 为T时 段，其 中T∈(t+t，t+t+t]，t∈T。

两架飞机的纵向距离表达式为

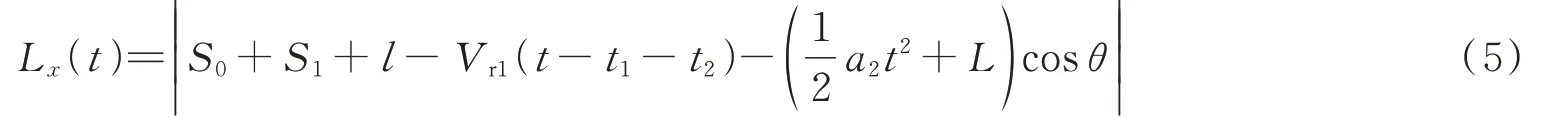
两架飞机的侧向距离表达式为

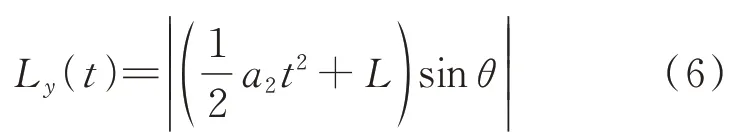
（4）T时段

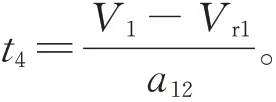
两架飞机的纵向距离表达式为

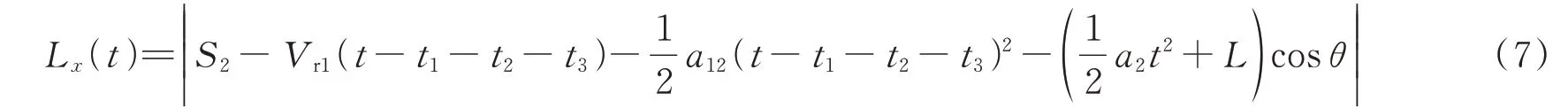
两架飞机的侧向距离表达式为

（5）T时段

当进场航空器北向复飞时，飞机1通过V点进行匀速转弯，该时段为T时段，T∈(t+t+t+t，t+t+t+t+t]，t∈T。

两架飞机的纵向距离表达式为

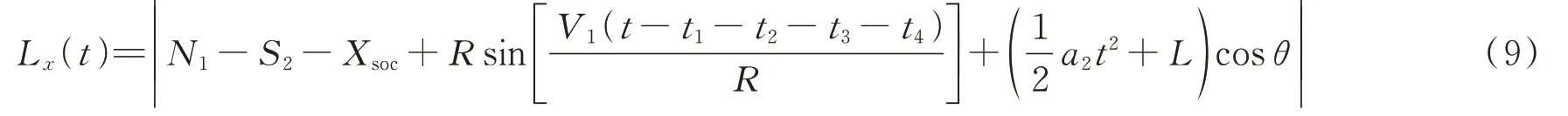
两架飞机的侧向距离表达式为

（6）T时段

飞机1匀速平飞转弯复飞结束后，进行直线匀加速爬升，在此期间与飞机2加速爬升存在一个高度差的交叉位置，最后飞机1到达V点，飞机2到达V点，至此结束。该时段为T时段，T∈(t+t+t+t+t，t+t+t+t+t+t]，t∈T。

两架飞机的纵向距离表达式为

两架飞机的侧向距离表达式为

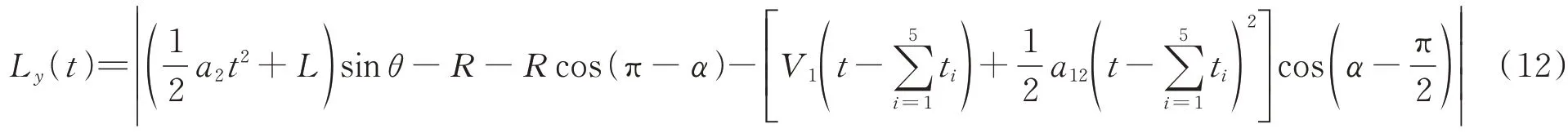
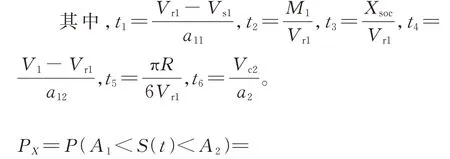
2.2 碰撞风险模型

设纵向碰撞风险概率为P，侧向碰撞风险概率为P，那么两架航空器在交叉跑道上的纵向和侧向碰撞风险模型分别为

式中：A为航空器机身长度之和的二分之一（符号为负）；A为航空器机身长度之和的二分之一（符号为正）；C为航空器翼展长度之和的二分之一（符号为负）；C为航空器翼展长度之和的二分之一（符号为正）；μ（i=1表示后机，i=2表示前机，下同）为纵向加速度误差均值；σ为纵向加速度误差方差；μ为侧向加速度误差均值；σ为侧向加速度误差方差；μ为由于导航误差因素所引起的偏差，代表航空器在纵向方向上的偏航距离的平均值；σ

为导航系统在纵向方向的方差。

3 复飞航迹与起飞航迹交叉时尾流模型

尾流模型主要包括尾流消散模型和尾流运动模型，文献［16］描述了尾流三个阶段的演化过程，即远地运动阶段、近地运动阶段和地效影响阶段，在每个涡流阶段，通过方程组来求解涡流的运动轨迹过程。

假设复飞航空器1的位置坐标 为(x，y，z)，则在两机之间的水平距离小于最小尾流间隔且高度差小于300 m的时间范围内，复飞航空器1第n秒的位置坐标为(x，y，z)，其 中n代 表 第n秒的时间，n=1，2，3，…；起飞航空器2的位置坐标为(x，y，z)，则起飞航空器2在第n秒的位置坐标为(x，y，z)，而起飞航空器产生的尾流坐标为(x，y，z)，其中i=1，2，3，…。

为了便于表示每一秒产生的尾流影响坐标，可以把尾流坐标用向量表示，假设复飞航空器1与起飞航空器2之间水平距离小于最小尾流间隔的开始时间为n，结束时间为2n，再设第n秒时向量a=(x，y，z)，第n+1秒 时 向 量b=(x，y，z)，第n+2秒时向量c=(x，y，z)直至第2n秒时向量为w=(x，y，z)，则每一秒起飞航空器产生的尾流影响坐标如下。

第n秒时，飞机的尾流坐标向量为

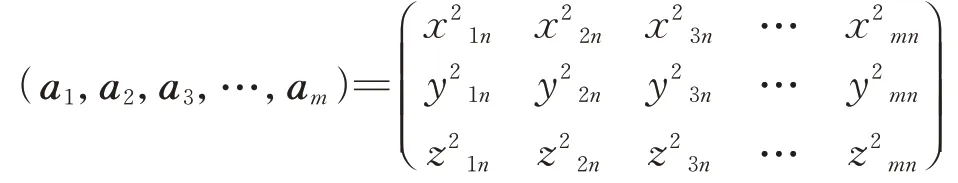
第n+1秒时，飞机的尾流坐标向量为(b，b，b，…，b)=

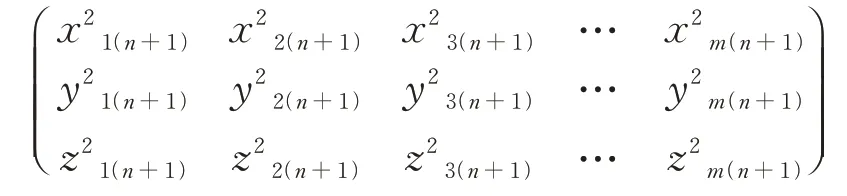
第n+2秒时，飞机的尾流坐标向量为

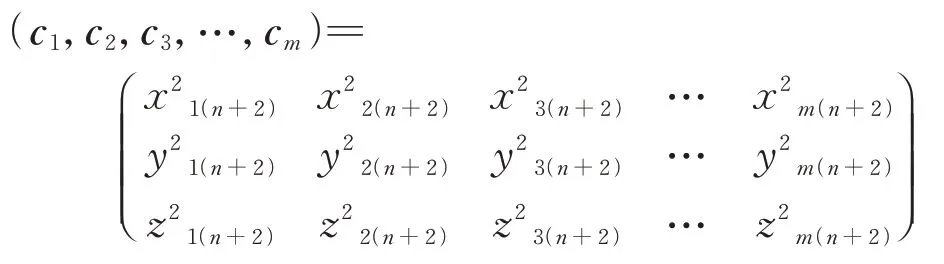
直至第2n秒时的尾流坐标向量为(w，w，w，…，w)=

复飞航空器1第n秒的位置坐标也用向量表示，即A=(x，y，z)，因此复飞航空器1全程飞行轨迹的坐标向量为

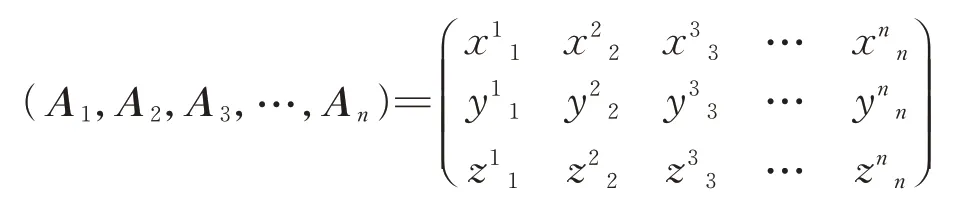
如果要保证复飞航空器1与起飞离场航空器2出现航迹交叉时安全，也就是复飞航空器1避免受到起飞离场航空器2的尾流效应影响，只需要把复飞航空器1的飞行轨迹位置坐标向量列元素不在每一秒起飞航空器产生的尾流影响坐标向量列元素内即可，即向量A中的坐标列元素在每一秒产生的尾流影响坐标向量a、b、c、…、w中的坐标列元素不落入尾流坐标范围。

因此，如果要保证尾流的安全间隔，只需要找出复飞航空器1的飞行轨迹坐标不落入到离场航空器每一秒产生的尾流运动坐标向量a、b、c、…、w中的运动坐标范围内即可。可以根据复飞航空器的速度V求出航空器1至跑道端的距离，也就是航空器在该距离之内，航空器2不得起飞，在该距离之外，航空器2可以起飞。需要根据不同速度V的变化来首先确定航空器1至跑道端的距离，其次判断两机之间水平距离小于最小尾流间隔时，起飞航空器2产生的尾流对复飞航空器1是否有影响；如果有影响，那么在V速度确定下，航空器1至跑道端的距离就不符合。

4 算例分析

大兴机场的交叉跑道有东一跑道（01L）与北一跑道（11L），根据第2节建立的碰撞风险模型和第3节建立的尾流间隔模型，对大兴机场交叉跑道的安全间隔进行求解。

选用B747-800作为起飞航空器，B737-800作为进场航空器计算，各参数如表2～表3所示。

表2 交叉跑道的基本数据Table 2 Basic data of crossed runways

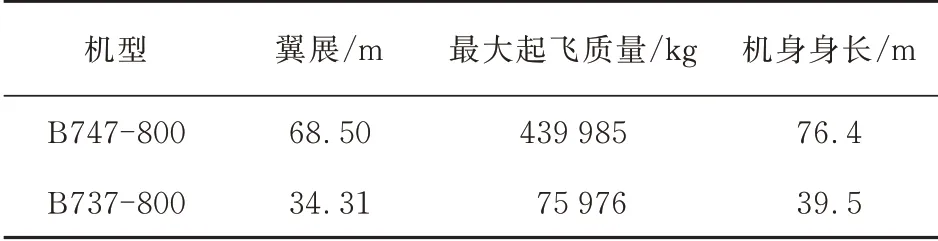
表3 前后航空器机型数据Table 3 Aircraft type data before and after

4.1 碰撞风险模型安全间隔计算

使用Matlab进行仿真，计算进场航空器至跑道端的不同距离值所对应的危险接近概率值，在可接受的安全目标水平内，找出符合距离值对应的安全目标水平值，确定距离跑道端位置的速度为75.25 m/s。仿真结果如图3所示，最终能够确定在距离跑道端的距离为4 984 m，对应的碰撞风险值为3.747×10次/小时，对应小于规定的目标安全水平值5×10次/小时。

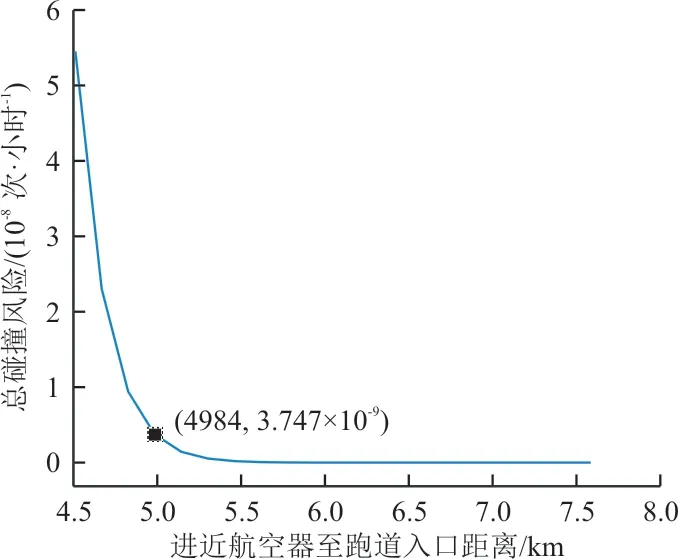
图3 总碰撞风险Fig.3 Total collision risk

4.2 尾流安全间隔计算

本文选取的前机（起飞离场航空器）为重型机，后机（进场复飞航空器）也属于重型机，根据尾流分类标准，两机之间的最小尾流间隔为5.6 km，因此只需要考虑小于6 km的范围内，前机对后机是否有影响。

首先根据碰撞风险模型的速度V确定其大小为75.25 m/s，然后计算出航空器1至跑道端的距离为4 984 m，即复飞航空器1距离跑道端4 984 m，而起飞离场航空器2产生的尾流对复飞航空器1是否有影响，分析过程如下：

首先计算出两架飞机水平距离小于6 km的时间范围，如图4所示，可以看出：当时间为57 s时，复飞航空器转弯爬升靠近起飞离场航空器，开始时间为57 s时，结束时间为108 s，在57～108 s之间两机之间的水平距离小于6 km；在57～108 s之间，起飞航空器2始终在进场复飞航空器1的高度之上，在106～108 s时间范围内，由于两机高度差在300 m之上，对于106～108 s之间无需考虑尾流影响。最终尾流影响的时间范围为57～106 s之间，起飞航空器2对进场复飞航空器1存在尾流影响。

图4 两机水平距离小于6 km的时间范围Fig.4 The time range when the horizontal distance between the two aircraft is less than 6 km

计算离场航空器在156～539.3 m的高度范围内，飞机在每一个高度产生的尾流变化位置坐标；尾流环量随着时间t的变化如图5所示，计算该尾流坐标时，只需要结束时间为尾流环量等于0的时间即可。从图5可以看出：在115 s时，尾流环量为0.56 m/s，可以认为该环量大小对飞机没有影响。

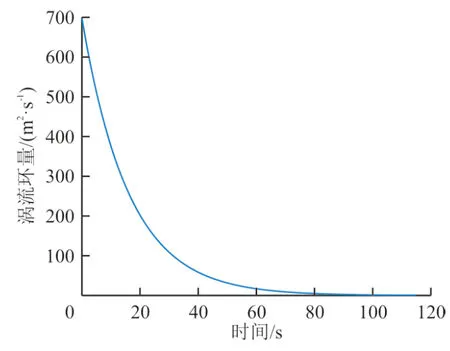
图5 尾流环量的变化大小Fig.5 The magnitude of the change in wake circulation

根据尾流三个阶段的坐标变化，可以求出尾流横向位置和垂直位置的运动坐标，再把尾流二维坐标系转化成三维坐标系，57～106 s的尾流坐标和进近复飞航空器坐标轨迹范围如图6所示。

图6 航空器轨迹和尾流坐标范围Fig.6 Aircraft trajectory and wake coordinate range

从图6可以看出：进近航空器在57～106 s之间的某一时间段，飞机轨迹位置坐标落入至离场航空器在57～106 s之间产生的尾流坐标范围之内，因此通过碰撞风险模型计算的ADW边界值4 984 m受到尾流影响，该ADW边界不满足要求，需要对ADW窗的边界值进行调整。

使其将ADW窗的边界值增加，分别计算ADW窗是5.22和5.42 km，是否有尾流影响，计算结果如图7所示。

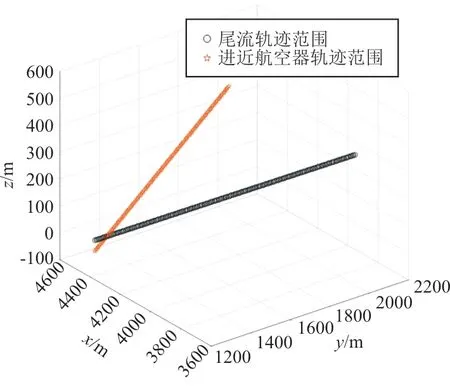
图7 ADW窗5.22 km的尾流影响Fig.7 Wake impact of ADW window 5.22 km

从图7～图8可以看出：在ADW窗是5.22和5.42 km的条件下，当ADW窗为5.22 km时，离场航空器对进近复飞航空器产生尾流影响，因此该ADW窗不符合要求；当ADW窗为5.42 km时，离场航空器对进近复飞航空器产生没有产生尾流影响，因此该ADW窗符合要求。综上所述，通过改变初始速度的不同值可以得到最终的ADW窗为5.42 km。为了保证安全，航空器1至跑道端的距离安全裕度设定为6 km。

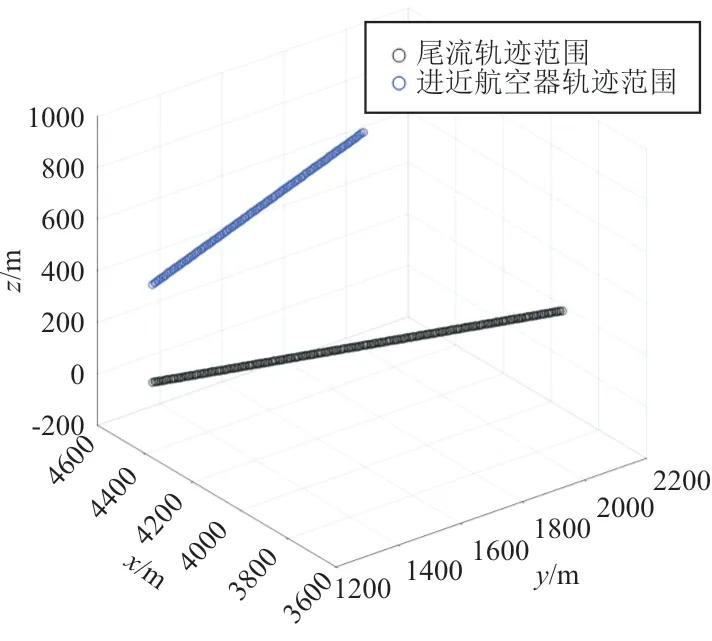
图8 ADW窗5.42 km的尾流影响Fig.8 Wake impact of ADW window 5.42 km

通过碰撞风险模型计算出的安全间隔边界值是4.984 km，而使用尾流间隔模型计算出的安全间隔边界是6 km，为了保证绝对安全，取两者较大值，即安全间隔的边界是6 km符合要求，该最小安全间隔值能够有效保证交叉跑道两架航空器之间的运行安全。考虑尾流因素时，并且对比现有大兴机场跑道运行标准间隔12 km，使得大兴机场交叉跑道运行标准间隔得到了优化。

4.3 不同交叉角度的ADW边界值

当交叉跑道的交叉角度，变化时这对于ADW的边界值是有影响，而且不同角度的ADW值是不同的，另外对于不同角度的交叉跑道，其碰撞风险值和尾流间隔模型计算的值都会与其密切相关。

取交叉角度步长为10°，这里计算常用机型B、C和M机型，其进近复飞不同机型组合的不同角度的ADW窗，通过Matlab仿真结果如图9所示。

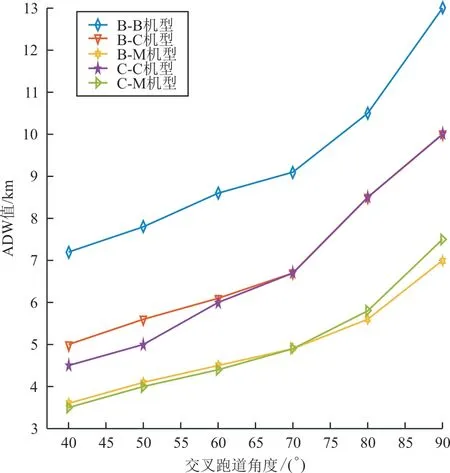
图9 复飞不同角度ADW值Fig.9 The ADW value of different angles of go-around

从图9可以看出：（1）该不同机型组合的ADW值是随着交叉跑道角度的增大而增大；（2）当进近航空器机型为重型机，离场航空器也为重型机时，相比较前后机为轻型机，所需ADW值越大，表明航空器机型的大小影响ADW值；（3）ADW值越大，对于管制员来说不利于指挥飞机进行风险规避。因此建立不同机型组合的ADW值，一方面有利于管制员根据不同机型的ADW值确定起飞离场航空器放行时机，另一方面也提升了运行安全效率。

5 结论

（1）本文根据碰撞和尾流模型计算进近航空器至跑到入口端的最小安全距离为6 km，即在大兴机场交叉跑道的一起一降模式中，两架航空器的安全间隔为6 km。

（2）通过综合考虑碰撞风险和尾流间隔模型，本文通过扩展不同角度下的ADW值，可对不同交叉跑道的ADW进一步优化和划分。