基于POD-BPNN模型的热启动策略及其在气动代理优化中的应用

贾续毅，李春娜，常琦，季稳

（1.西北工业大学陕西省空天飞行器设计重点实验室，西安 710072）（2.火箭军装备部 装备项目管理中心，北京 100085）

0 引言

随着计算机技术的发展，计算流体力学（Computational Fluid Dynamics，简称CFD）成为获取高可信度气动数据的主要手段并被大量应用于气动优化设计。梯度优化算法和启发式优化算法是当前常用的气动优化设计算法。相比于梯度优化算法，差分进化（Differential Evolution，简称DE）算法、粒子群算法等启发式优化算法具有更好的全局搜索能力，从而在气动优化中得到广泛使用。但是，该类算法在气动优化过程中需要进行成千上万次CFD仿真，导致优化效率低下。为了兼顾全局搜索能力和优化效率，代理优化（Surrogatebased Optimization，简称SBO）应运而生。

SBO具有设计效率高、全局优化能力好、鲁棒性高等特点，在具有高维设计变量、多目标等工程优化问题中具有良好的应用前景。目前已发展了Kriging模型、径向基函数（Radical Basis Function，简 称RBF）、多 项 式 混 沌 展 开、神 经 网络等多种代理模型建模方法。在气动SBO中，代理模型建立了从气动外形参数到气动力的映射关系。SBO本质上降低了CFD计算次数但没有改善单次CFD计算时间，且没有有效使用CFD的流场信息。

机器学习技术在气动力建模、流场降阶、流动特征提取等流体力学领域得到大量应用和发展，S.A.Renganathan等使用深度神经网络和高斯过程实现了气动外形的优化设计，但该方法仍为梯度优化；Sun Z W等、Huang D M等使用具有特征提取能力的降阶模型如本征正交分解（Proper Orthogonal Decomposition，简称POD）和具有高效建模能力的神经网络模型建立了从气动外形参数到流场信息的映射关系，实现了流场预测。常用的神经网络包括反向传播神经网络（Back Propagation based Neural Network，简 称BPNN）、径 向 基 函 数 神 经 网 络等，Zhu L等使用径向基函数神经网络构建的涡黏预测模型代替了CFD求解中的湍流模型，通过与N-S方程耦合求解降低了单次CFD计算时间，但是该方法需要对CFD求解器进行相应修改，对于优化设计人员，鲜见成熟的、已嵌入湍流建模的求解器可供使用。

本文以气动优化为研究对象，首先，结合SBO和机器学习流场预测模型的特点，提出一种基于本征正交分解—反向传播神经网络（POD-BPNN）模型的热启动策略，并将其嵌入SBO；然后将该策略应用于跨声速翼型减阻优化，并对优化结果进行分析；最后通过案例对优化效率、POD-BPNN的流场预测性能、热启动策略的效果进行分析。

1 优化策略

1.1 优化总流程

气动优化中所涉及的单目标优化问题可以表示为

针对以上气动优化问题，本文结合SBO和POD-BPNN流场预测模型，提出一种基于PODBPNN的热启动策略并将其应用于气动代理优化。以翼型气动减阻优化为例，优化策略的总流程如图1所示，具体分为以下5个步骤。

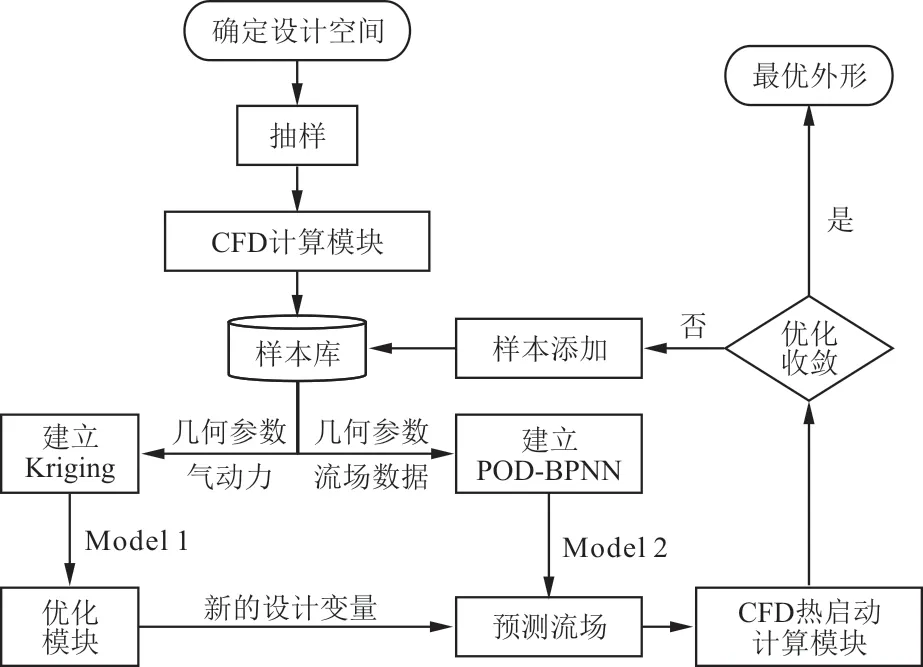
图1 优化流程Fig.1 Procedure of the optimization

（1）生成初始样本库

使用拉丁超立方抽样（Latin Hypercube Sampling，简称LHS）在几何设计空间中抽取r-1组几何参数，并与基准外形共同构成初始外形库，共计r个外形。然后生成基准外形的气动网格，并基于该网格利用RBF网格变形技术生成其他r-1个外形的气动网格。RBF网格变形方法具有良好的鲁棒性和较高的计算效率，可以解决复杂的网格变形问题，并在后续气动优化过程中也使用该方法获得气动网格。最后通过CFD计算模块得到r个外形的流场数据和气动力。

（2）建立初始气动预测模型

使用Kriging模型直接建立从几何参数到气动力的气动力预测模型Model 1，使用POD和BPNN建立从几何参数到流场数据的流场预测模型Model 2，具体建模流程如图2所示。

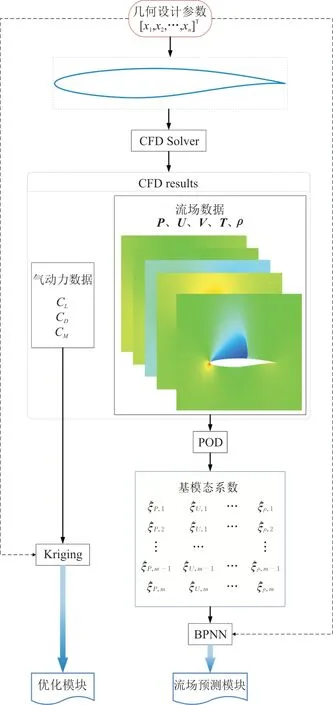
图2 气动预测模型Fig.2 Procedure of the aerodynamic prediction model

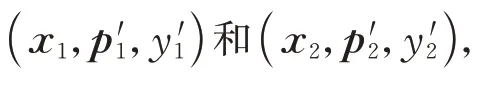
（3）流场预测及CFD热启动计算

对于优化模块得到的两组新的设计变量，通过Model 2预测相应的流场数据Y′和Y′，预测过程详见1.5节；并将Y′和Y′作为CFD热启动计算的初场进行热启动计算，计算得到真实气动力p、p，真实目标函数y、y和真实流场数据Y、Y。

（4）更新气动预测模型

每完成一轮CFD热启动计算，判断优化是否终止，若判断出优化仍将继续，则将新样本添加到样本库。由于Kriging建模效率高，每完成一轮CFD热启动计算，就将(x，p，y)和(x，p，y)添加到Kriging模型并重新建立Model 1；而PODBPNN模型的建模效率较低，每完成k轮CFD热启动 计 算，把2k个 样 本 流 场 数 据(x，Y)，j=1，2，…，2k，添加到POD-BPNN模型并重新训练得到新的Model 2。

（5）重复进行步骤（2）～步骤（4），直到优化终止。

1.2 Kriging模型

Kriging模型具有较好的非线性拟合能力，能够提供插值点的预测函数值和统计学误差估计信息，该误差估计信息可以用于动态加点，因此，本文使用Kriging模型用于气动代理优化过程。

Kriging模型可以表示为

Kriging模型的具体推导详见文献［5］。

1.3 POD模型

具有高维、复杂特征的流场数据可以通过降阶模型实现其在低维空间的映射和流场特征的提取。在气动优化问题中会生成一定规模的高维流场数据，可以通过建立POD降阶模型，将高维流场数据近似表示为若干阶基模态的线性叠加。

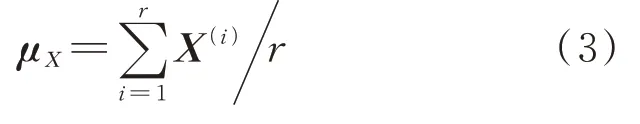
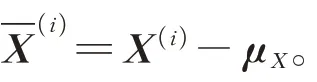
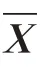
当前s阶基模态的能量占比达到一定值时，X()

能够以低误差率近似表示为

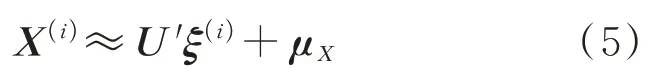
式中：U′为U的伪逆矩阵。

通过POD降阶模型实现了高维数据X到低维基模态系数ξ的映射。除了上述一般的POD求解方法，还有Snapshot-POD、基于SVD分解的POD等，它们的区别只是求解方法不同，但都会获得相同的POD基模态等信息。通常，当m≪r时，使用一般的POD可以加快速度节省计算内存；当m≫r时，使用Snapshot-POD可以加快速度节省计算内存。

1.4 BPNN模型

BPNN作为神经网络的一种，对较低维度的多输入多输出数据具有较强的非线性拟合能力。典型的单隐含层BPNN架构如图3所示，图中输入层、隐含层和输出层的神经元分别用x(i=1，2，…，n)、z(j=1，2，…，b)和y(k=1，2，…，s)表示，该模型实现了n维输入到s维输出的建模。通过调整隐含层的层数、各层神经元个数、各层间的激活函数类型、学习率等超参数，可以使模型具有较好的拟合能力和泛化能力，实现对新样本输出值的稳健预测。BPNN的具体建模过程详见文献［27］。

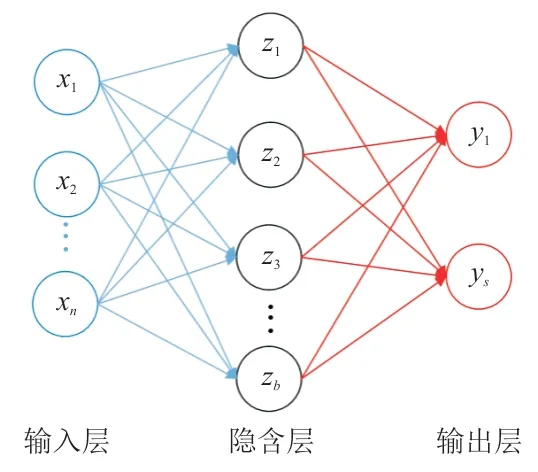
图3 BPNN架构Fig.3 Architecture of BPNN

1.5 POD-BPNN流场预测模型

结合POD模型和BPNN模型，可以构建出POD-BPNN流场预测模型。

针对在设计空间中抽样获取的r组二维外形，其几何设计参数为x(i=1，2，…，r)，x为n维列向量，通过CFD计算得到对应的流场数据：压强P、速度U、速度V、温度T、密度ρ，这五个物理场数据均为m×r阶矩阵，m为气动网格的网格数量。以 压 强 场P=[P，P，…，P]（P为m维 列 向量）为例，对其建立POD模型，得到压强场均值μ（m维列向量）、基模态系数ξ（s维列向量）、映射矩阵U（s×m阶矩阵），且有：

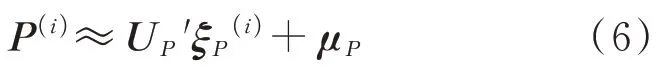
对几何设计参数x和基模态系数ξ建立BPNN模型，模型的输入维度为n，输出维度为s。把训练好的BPNN模型所表征的输入输出映射关系记为ψ，即ξ=ψ(x)，则通过POD和BPNN可以建立几何设计变量x和压强场P的映射关系：

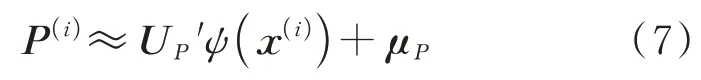
式（7）为POD-BPNN流场预测模型。

对于设计空间的任一设计变量x，可以通过POD-BPNN模型中的BPNN预测其基模态系数ξ：

然后通过POD模型的μ和U重构出压强场的预测值P：

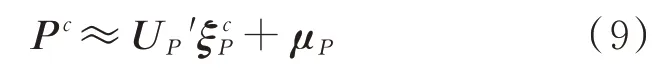
同样可以通过对物理场U、V、T、ρ建立PODBPNN模型，从而快速获得这些物理场的预测值，具体预测流程如图4所示，模型的输入为几何设计变量，由优化模块给出；模型的输出为各个物理量的流场预测数据，并作为计算初场传递给CFD热启动计算模块。

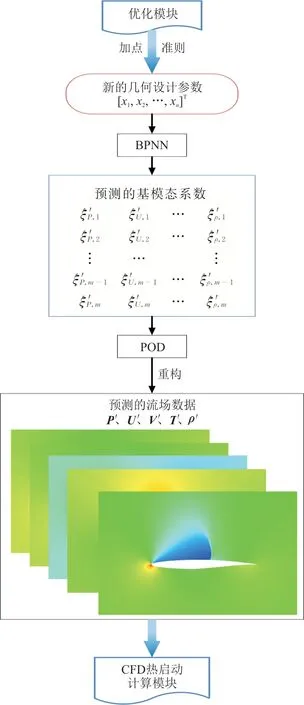
图4 使用POD-BPNN进行流场预测Fig.4 Prediction of the flowfield by POD-BPNN

1.6 效率分析

对于气动代理优化中是否应用基于PODBPNN的热启动策略进行计算时间分析对比。优化的初始样本个数为r，优化过程共调用λk+b次优化模块，其中λ，k∈N，b=0，1，…，k-1。当不使用基于POD-BPNN的热启动策略时，优化总时间T为

当使用基于POD-BPNN的热启动策略时，优化总时间T为

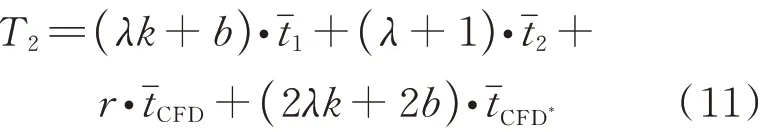
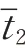
可以得到如下关系：

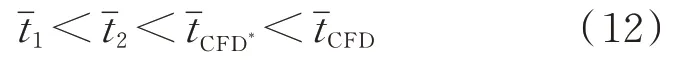
使用基于POD-BPNN的热启动策略，气动代理优化的时间节省量Δ为

2 案例分析

2.1 优化问题描述

本文以RAE2822翼型为优化的基准翼型，优化 设 计 工 况：Ma=0.734，α=2.79°，Re=6.5×10，优化问题的数学模型为

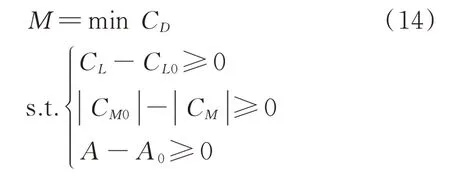
式中：C、C和C分别为当前翼型的升力、阻力和俯仰力矩系数；C和C分别为基准翼型的升力和俯仰力矩系数；A和A分别为当前翼型和基准翼型的面积，为无量纲化数值。

2.2 参数化及网格收敛性分析

本文采用CST（Class-function Shape-function Transformation）参数化方法，采用6阶伯恩斯坦多项式，共14个设计变量。基准翼型网格收敛性分析如表1所示，表中网格均采用结构/非结构混合网格形式，这四套网格的物面网格疏密程度不同，根据C和C的数值对比确定出气动优化所使用的气动网格为Ⅲ，网格数量约为4.7万，远场边界为70c（c为翼型弦长，这里c取无量纲数1）；物面第一层网格高度为5.0×10c。采用网格Ⅲ得到的CFD仿真结果与实验值以及文献［7］中仿真结果对比如表2所示，翼面压力系数分布与实验值的对比如图5所示，可以看出：本文的升力系数计算结果与实验值相差不到3%；阻力系数与实验值相差不到5%；力矩系数与实验值相差不到11%，与文献［7］相差不到3%；压力系数分布曲线与实验值基本吻合，说明本文的CFD计算具有一定准确性。

表1 基准翼型的气动网格收敛性分析Table 1 Grid convergence analysis for the baseline

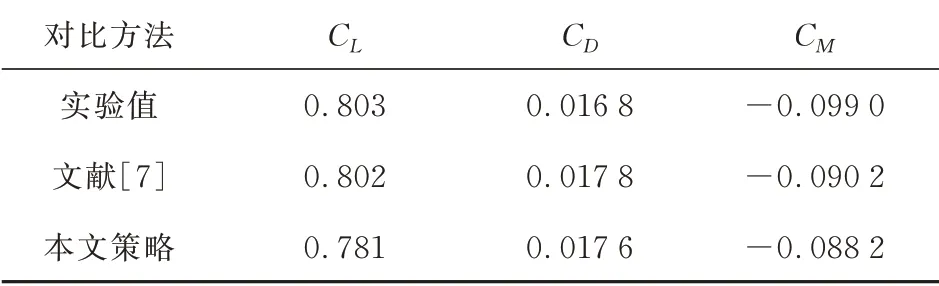
表2 基准翼型的力系数计算结果对比Table 2 Validation of CFD simulation for the baseline

图5 RAE2822翼型压力系数分布与实验值对比Fig.5 Comparison of pressure coefficient distribution of RAE2822

基准网格为网格Ⅲ。使用RBF网格变形技术获得其他外形的气动网格，网格变形前后的气动网格对比如图6所示，可以看出：变形后网格的网格质量与基准网格基本保持一致。

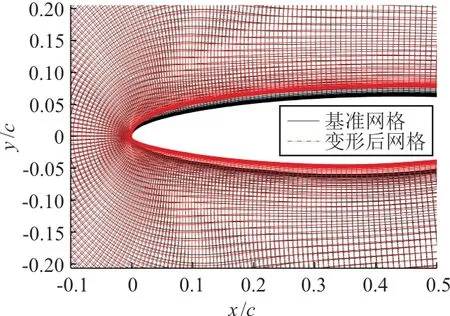
图6 网格对比Fig.6 Comparison of grids

2.3 优化参数设置

初始样本通过LSH获取，抽取个数为n( )n-1 2，n为设计变量个数，剔除计算不收敛样本，得到有效样本89个。优化中参数k的取值为5，即每完成5轮优化模块的调用，进行一次PODBPNN预测模型的更新，既可以保证流场的预测精度，又能够避免由于重复建立POD-BPNN而降低模型效率。

2.4 优化结果及分析

目标函数随着加点个数的收敛历程如图7所示。优化前后的气动性能对比如表3所示，可以看出：对比基准翼型，优化后阻力系数C降低了约0.006 3，优化得到的翼型相比于基准翼型阻力系数减小了35.8%，升力系数、面积和力矩系数均满足约束条件。

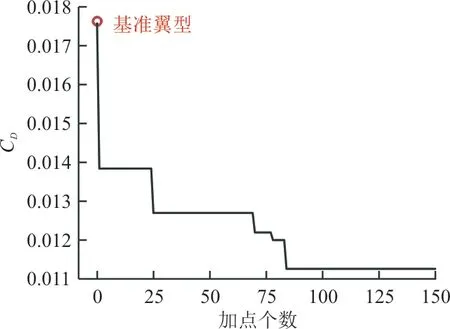
图7 目标函数的收敛曲线Fig.7 Convergence curve of goal function

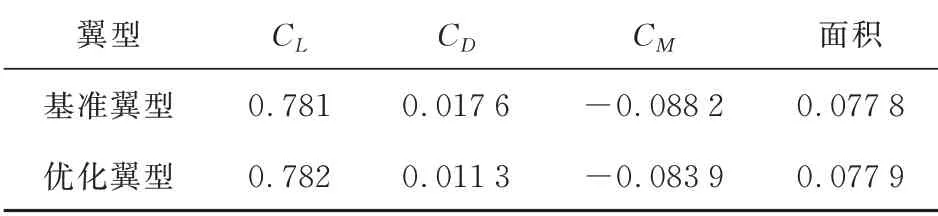
表3 优化前后的气动性能对比Table 3 Compare of aerodynamic performance of baseline and optimum shape

优化前后的翼型几何形状和翼面压力系数分布对比如图8～图9所示。

图8 优化前后翼型对比Fig.8 Compare of baseline and optimum shape

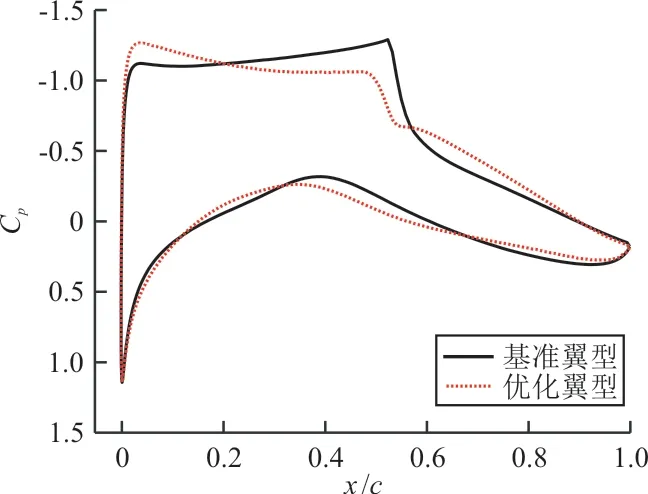
图9 优化前后翼面压力系数分布对比Fig.9 Comparison of pressure coefficient distribution of baseline and optimum shape

优化前后翼型的压强场云图对比如图10所示，可以看出：优化后上表面的强激波得到有效削弱，减阻优化效果明显。

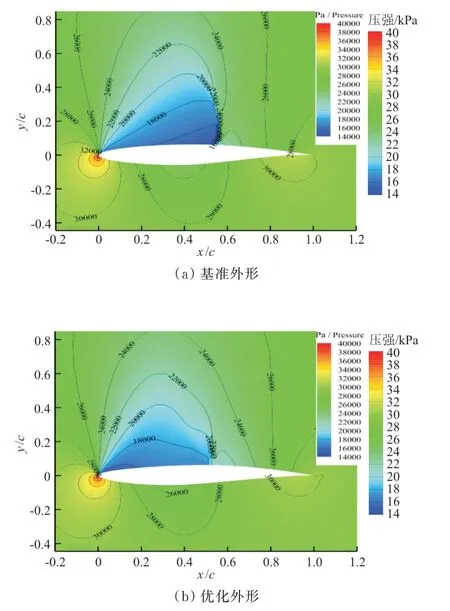
图10 优化前后压强云图对比Fig.10 Comparison of pressure field of baseline and optimum shape

由于POD-BPNN仅在SBO中加入样本预测流场及CFD热启动计算，不会对SBO的相关参数、优化过程和优化结果产生影响。因此仅对本文策略和SBO进行效率对比分析，结果如表4所示，可以看出：本文策略相比于SBO，单次CFD计算时间降低约68%，整体效率提升约37%。

表4 计算时间分析Table 4 Time-consuming analysis

在SBO中使用POD-BPNN对某一新加样本点的流场预测效果如图11所示，可以看出：PODBPNN在上翼面距离前缘60%c位置附近的压强预测效果较差，而在非激波位置处的等压线拟合均较好。

图11 POD-BPNN对压强场的预测效果Fig.11 Forecast result of pressure field by POD-BPNN

给出最优外形下两个方法的收敛曲线如图12所示，可以看出：CFD需要约900步完成C和C的计算收敛，而使用基于热启动策略的CFD计算仅需200步左右就可以完成C和C的计算收敛。

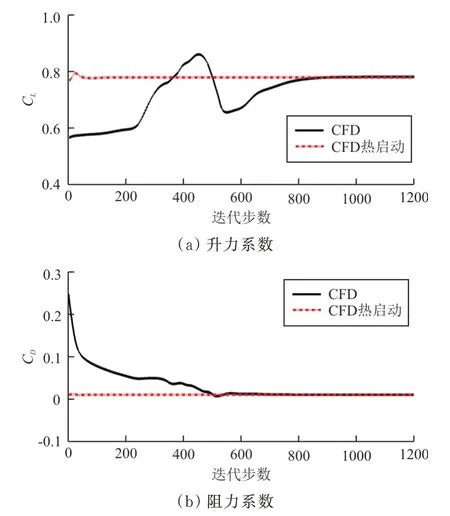
图12 两种方法的收敛曲线Fig.12 The convergence curves of the two methods

在整个代理优化过程中，初始样本和新加样本点的CFD计算的收敛步数如图13所示，其中使用CFD计算的初始样本收敛步数，数值集中在800步左右；采用基于POD-BPNN热启动策略的新加样本点的计算收敛步数，数值集中在200步左右，新加样本点在使用基于POD-BPNN模型的CFD热启动计算后，其收敛步数整体上低于使用CFD计算的初始样本收敛步数，CFD热启动计算失败的情况主要集中在加点的前期。热启动计算失败的样本量为9个，占整个热启动样本量的5.8%，当在计算中出现该情况，只需切换为CFD计算即可。

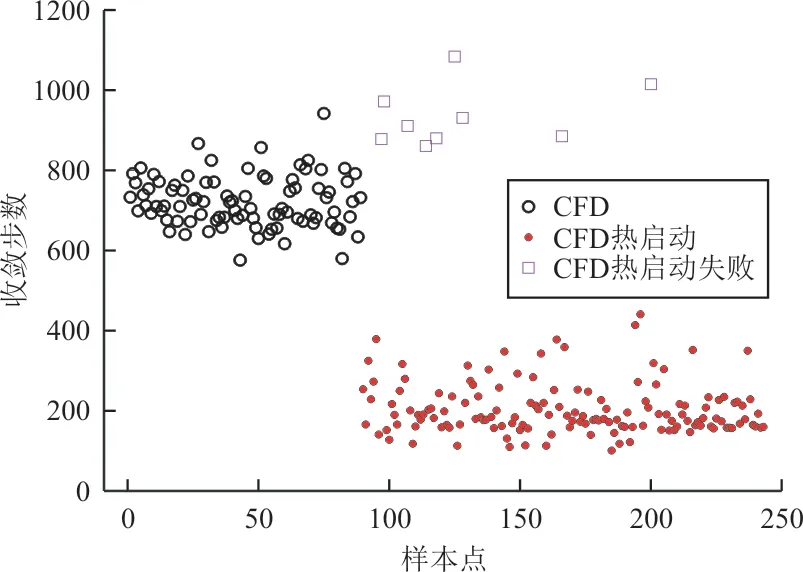
图13 气动计算的收敛步数分析Fig.13 Analysis of convergence steps for aerodynamic calculation

POD-BPNN模型对每个新加样本点压强场的预测均方根误差如图14所示，可以看出：预测误差呈现初期大、后期小的趋势，这与图13中CFD热启动失败集中在加点前期的现象是一致的。

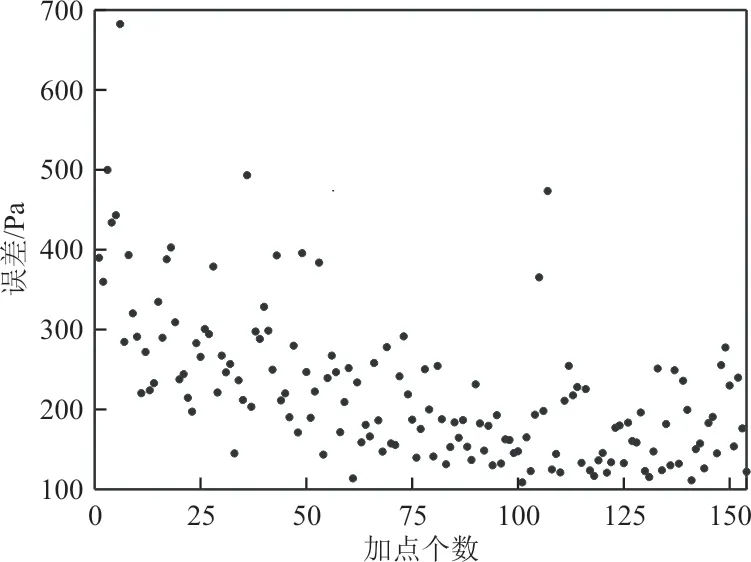
图14 POD-BPNN模型对压强场的预测误差Fig.14 The RMSE of pressure flowfiled by POD-BPNN

3 结论

（1）针对翼型跨声速减阻优化算例，使用基于POD-BPNN模型的热启动策略进行气动代理优化，获得了减阻明显的优化翼型，在优化中单次CFD计算时间降低了68%，整体优化效率提升了37%。

（2）由于POD-BPNN模型的建立相比于Kriging需要耗费一定时间，但是Kriging模型随着优化模块的调用实时更新；而POD-BPNN模型在调用多次优化模块后再进行更新，可以有效提高建模效率。

（3）POD-BPNN流场预测模型中使用了POD，而POD的建模效率很高，因此POD-BPNN的建模效率与网格量的相关性较小。在气动网格数目较多的三维外形气动优化中，该策略的引入使得优化效率的提升更加显著。

（4）使用POD-BPNN模型的预测流场作为初场进行CFD热启动计算可能会产生计算不收敛的情况导致计算失败，该比例不超过6%。可以通过提高模型预测精度来有效降低热启动计算失败的概率。