考虑随机运输提前期的供应链网络研究

李明雨 武晓民

（1.北京科技大学天津学院 天津 301800；2.中国人民解放军96881部队 河南洛阳 471000）

供应链网络设计(SCND)是确定工厂、仓库和配送中心的数量、位置、产能，市场区域分配，供应商选择，原材料和产品在供应链网络各层级之间的流动。在当今竞争激烈的世界中，决策者需要考虑不确定因素，以保持竞争力，特别是在SCND问题背景下，对不确定性影响的研究是文献中最关注的问题。

王珂等（2020）建立了基于在线价值的物流网络规划模糊两阶段模型，通过理论分析和证明将其转化为等价的确定阶段规划模型进行求解，降低了计算难度且得到了模型的精确解。Chen等（2007）提出了不确定需求环境下的多目标混合整数模型，使总成本、运输时间最小，稳健性最大化。Xu等（2009）开发了一个随机模糊规划模型来解决考虑随机需求和供应商容量的多阶段SCD问题，将模型转化为等价整数规划，利用遗传算法对模型进行求解。Gumus等（2009）提出了一种集成神经模糊混合整数线性规划方法来设计需求不确定下的三级供应链网络，通过建立神经模糊模型对需求数据进行预测。梁爽（2020）研究了带有模糊时间约束的多周期、多车型混合运输配送网络优化模型，采用微粒群智能优化算法进行求解，验证了该模型对企业做出长期决策具有良好的指导作用。曲孟等（2017）建立了考虑多运输方式的模糊随机规划供应链模型，并在相应的隶属度水平和置信水平上将其转化为确定的线性规划模型。Jolai等（2011）提出了一种生产分配问题的模糊多目标线性规划模型，模型包括一个制造商、多个工厂、产品、配送中心、零售商和客户，采用遗传算法和粒子群优化算法进行求解。Sadeghi等（2018）开发了一个多产品两级供应链网络的库存系统仿真模型，假设运输提前期和需求是随机的，该模型的目标是最小化系统的成本，包括库存持有成本、运输成本和短缺成本。

综上所述，SCND问题经典模型的主要目标是最大化利润或最小化供应链网络成本，为了处理由于运输提前期的不确定性或供应链环境影响等因素造成的决策不精确，需要简化实际的供应链网络问题，对多个冲突目标进行优化处理。

1 构建数学模型

1.1 问题描述

SCND中每个工厂的产能都有限，制造成本取决于工厂的位置。考虑到运输时间和运输成本，将产品从工厂运输到配送中心，配送中心存储产品的能力有限，客户区域是供应链网络的目标节点。由于产品需求、提前期和销售价格存在随机特性，本文提出一种考虑随机运输提前期的模糊双目标混合整数非线性规划的SCND问题模型，既满足制造商利润最大化的需求，又满足客户对运输提前期不确定性的需求。模型考虑两个相互冲突目标：工厂与配送中心之间及配送中心与客户之间的总净利润最大化，与运输提前期相关的风险概率最小化，目标的模糊性使决策者能够考虑其可接受满意度来决定其SCND设计。将各节点运输时间和运输成本作为模型的参数，假设与运输提前期相关的可能风险遵循一个具有确定均值和标准偏差的正态分布，通过两个不同的风险等级对模型进行检验，以达到供应链网络满意度的最大值，模型计算结果帮助决策者更好地洞察与有利目标相关的供应链网络设计。

系统成本包括供应链各级之间的运输成本、开设新配送中心的成本、与工厂有关的制造成本。延迟概率确定了提前交付产品的风险，运输时间是随机的，服从正态分布。开设一个配送中心将增加提前概率，但是与第一个目标相冲突，它将增加新的成本。

1.2 符号描述

（1）、、：分别为工厂编号、配送中心编号、客户区编号。

（2）、、：分别为工厂数量、配送中心数量、客户区数量。

（3）F：开设新配送中心的成本；

（4）Tm 、Tdc ：分别为从工厂到配送中心和配送中心到客户区的运输成本。

（5）µ、µ：分别为从工厂到配送中心和从配送中心到客户区运输时间的均值。

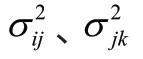
（7）MC、MP：分别为工厂生产能力和生产成本。

（8）DCC ：配送中心的容量。

（9）D、DD：客户的需求量和交货期。

（10）S P：顾客区的销售价格。

（11）、：分别表示评价利润、提前概率的满意度水平。

（12）ub、lb：分别为利润模糊约束的上限和下限。

（13）ub、lb：分别为提前概率模糊约束的上限和下限。

（14）：极大数字。

（15）、：分别为最大化利润和提前概率。

（16）X 、X ：分别为产品从制造厂到配送中心和从配送中心到客户区的流量；

（17）Y、Y ：分别表示如果存在从工厂到配送中心的链接和从配送中心到客户区的链接，则为1，否则为0。

（18）P：产品从制造厂到客户区通过配送中心运输的提前概率。

（19）L ：如果启用配送中心，则为1，否则为0。

1.3 数学模型

建立模糊随机混合整数非线性规划模型：

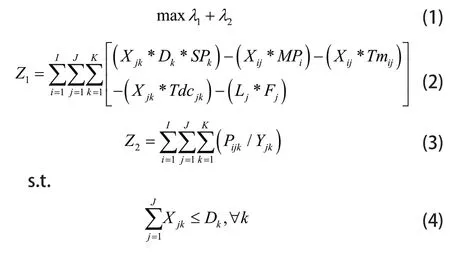
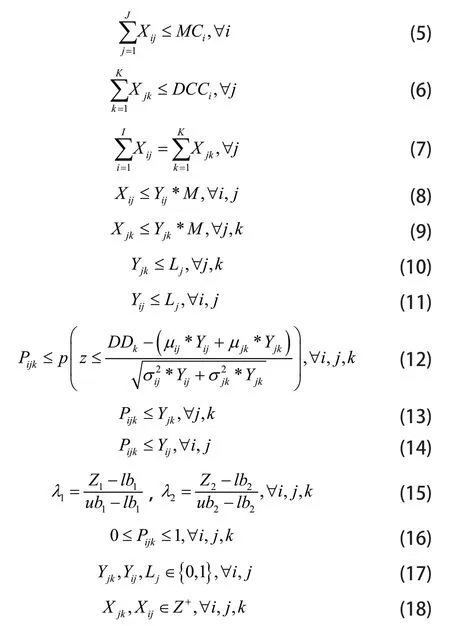
式（1）表示两个满意度之和最大化；式（2）表示利润最大化，第一项是指销售产品在客户区域的利润，第二项是指产品的制造成本取决于工厂，第三、四项分别确定了从起点到中间节点和从中间节点到目标节点的运输成本，第五项是指启用一个配送中心的成本；式（3）表示提前概率的平均值；式（4）表示从配送中心到每个客户区域的流量应小于或等于客户需求；式（5）表示从每个工厂到配送中心的流量应小于或等于制造能力；式（6）表示从每个配送中心到客户区域的流量应小于或等于配送中心的容量；式（7）表示每个配送中心的输入流量应等于输出流量；式（8）、式（9）分别表示如果从工厂到配送中心和从配送中心到客户区域的链路是开放的，则在该链路中就可能会有流量；式（10）、式（11）分别表示如果配送中心开放，从配送中心到用户区域和从工厂到配送中心的流量；式（12）表示将产品交付给客户，在考虑随机运输时间的情况下，从工厂到配送中心和从配送中心到客户区域的运输提前概率；式（13）、式（14）表示提前的概率应仅为存在的链路；式（15）分别表示利润和提前概率的满意程度；式（16）表示提前的概率介于0～1；式（17）表示该参数是0～1变量；式（18）表示参数是正整数变量。

2 模型求解算法

考虑随机运输提前期的模糊双目标混合整数非线性规划的供应链网络设计模型是非线性整数规划模型，目前关于这类问题的求解还没有通用的解法，属于较为复杂的一类数学问题。本文选择Lingo软件对问题进行编程求解，包括三个部分：定义集合、输入模型数据、编写计算段方程函数，具体编码过程如表1所示。

表1 模型算法的Lingo代码

3 数值实验

本文通过数值实验验证所提出的模型在供应链决策中的适用性，该实例包括2个工厂、4个配送中心和5个客户区域，初始数据如表2至表4所示，设置基本方案中的风险级别为50%。

表2 工厂相关信息

表3 配送中心相关信息

表4 每个客户区域的需求、到期日和售价

使用Lingo 17.0对模型进行编程求解，箭头上的数字显示了供应链不同层次的产品流量，指向客户箭头的末端数字表示到达客户的提前概率。图1表示风险水平为50%供应链网络流量，结果表明未启用配送中心4，因此三个配送中心足以满足既定风险的需求。图2表示风险水平为40%供应链网络流量，从工厂到配送中心 2和配送中心3的流量及从配送中心 3到客户区域4的流量发生了变化，以消除小于60%的提前概率。

图1 风险水平为50%供应链网络流量

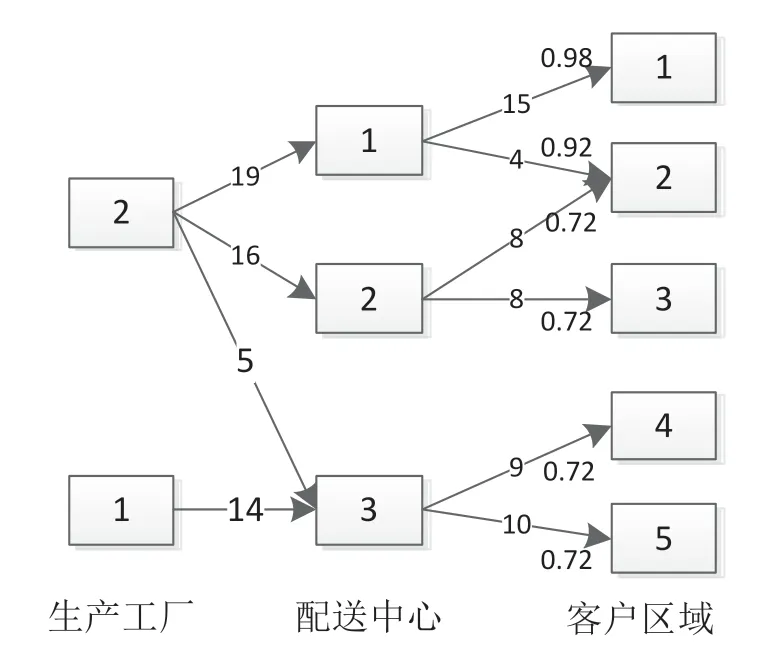
图2 风险等级为40%供应链网络流量

表5总结了不同方案下利润的下界、上界和目标函数值，将风险水平从50%降低到40%，获得的利润更少。原因是为了增加提前期概率，增加了运输成本，导致利润减少。

表5 与不同风险等级相关的目标函数、下限和上限

4 结语

本文重点探讨供应链系统中延迟概率与利润两个相互冲突目标之间的权衡问题，因此应用模糊逻辑理论阐明决策者对每个目标的投资。由于存在随机运输提前期，导致了向客户交付产品的不确定性。模型包含100个变量，其中28个非线性变量、60个整数变量，其余为0～1变量；共有172个约束条件，其中80个是非线性的。在Core i7-7700 CPU @3.60 GHz PC（16 GB内存）计算机上的计算时间从30秒到5分钟不等。从实验结果可以看出，随着风险水平的降低，提前期发生的概率呈线性关系增加，但利润下降。文中提出的模型已通过适用于小规模数据集的测试，为了在实际的供应链系统中应用该方法，需要增加网络的规模。因此，对于处理大规模的计算问题，建议将约束条件线性化以减少计算时间，或应用元启发式算法求解。