金属零部构件激光熔覆工艺参数优化的数学建模设计

段 佩，龚加安

(商洛职业技术学院，陕西 商洛 726000)

随着我国工业水平的不断提升，化工工业、胶粘剂制造发展迅猛。工业设备和制造领域需要更多的零部构件，而当前的零部件制造技术由于条件限制和技术不足的原因，导致生产复杂部件的难度加大、材料损耗严重，从而使得工作效率低下，无法满足日益增长的复杂零部件的制造需求和个性化需求；因此，新的制造技术随之诞生。在众多金属制造技术中，应用最为广泛的技术为激光熔覆成形技术，该技术主要通过激光的方式对工业构建进行制造和修复等。但该技术的应用效果取决于各种工艺参数的设置，如何将各参数设置到最佳，并取得最好的激光融履效果成为当前众多学者研究的重点。有学者提出了基于径向基函数神经网络和NSGA-Ⅱ的气保焊工艺多目标优化方法，进一步提升了激光熔覆工艺水平和性能；基于改进粒子群-禁忌搜索算法的FMS布局优化，通过遗传算法确定了最优工艺参数，最终实现了激光熔覆工艺参数的多目标优化；马氏体不锈钢电弧增材制造工艺优化及焊缝几何特征，通过构建GRNN神经网络模型和激光熔覆工艺参数进行回归分析，实现了电弧增材制造工艺的优化，并降低了工艺难度。基于此，本研究结合以上学者研究成果，以激光熔履技术为研究对象，通过对其工艺参数进调整和优化，以此提高工业制造品的质量和精度。

1 工艺参数多目标优化模型建立

1.1 多目标优化模型建立

为更好优化化工工艺，本研究基于激光熔覆的工艺参数，建立多目标优化模型。通过GRNN 回归模型，表现熔覆层性能参数与工艺参数二者间的关系。若=(,,)，式中：为第个性能指标(=1,2,3,4)；为激光功率；为扫描速率；为送粉速率。

优化模型主要包括变量、约束条件和目标函数3个部分。本研究综合考虑当前工业制造品的实际条件，构建了优化模型。

变量

激光功率设置为(、2)；扫描设置为(、3)；送粉速率设置为。

约束条件

由于工业设备对上述3种工艺参数影响较大，因此参数设置必须满足设备的规定和要求。本研究根据其制定相应的约束条件。具体设置：

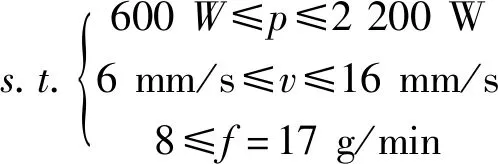
(1)

目标函数

在激光熔覆层中，显微硬度与力学性能成正比关系,硬度越高，性能越好；稀释率与化学成分成反比关系，稀释率越小，表明激光熔覆性能更好；热影响区深度取值越小，性能更好。由此得到相应的目标函数：

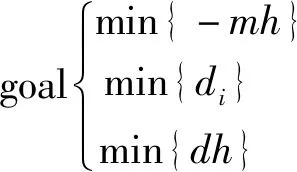
(2)

式中：显微硬度表示为=(,,)；稀释率表示为=(,,)；热影响区深度表示为=(,,)。

1.2 多目标优化方法

Pareto 解集

在激光熔覆层中，多目标优化与目标函数可能有很多，其求出的解不能保证均是最优解。因此，本研究采用计算非支配解，即Pareto 解来解决此问题。若目标函数有个，表示为(),=1,2,…,；其中解支配解可表示为：

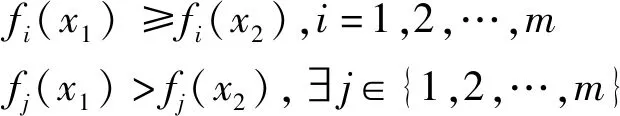
(3)

若要选择一个最优解，需从Pareto 解集进行选取。通过 Pareto 解形成的曲面也可称之为Pareto最优前端，Pareto解集主要包括非支配解，受支配解和Pareto最优前端。

多目标优化方法

多目标优化方法主要包括2种类型：一种是由多目标转化为单目标优化问题，即主要目标法、统一目标法等；另一种类型为直接对Pareto 解集进行计算，从而求出最优解，即多目标进化算法、多目标粒子群算法等。本文结合激光熔覆层的结构特点，选择使用多目标进化算法优化分析上述中建立的多目标优化模型。

2 基于NSGA-Ⅱ的多目标优化

多目标进化算法属于一种智能算法，当前应用最多的多目标优化算法为NSGA-Ⅱ算法。

该算法是基于NSGA-Ⅰ算法，加入拥挤距离排序和精英策略，算法原理是对生物种群进化过程进行模拟，通过在原始种群中进行多次交叉变异后得到新的种群，将适应度最高的新种群进行保存，通过若干次迭代更新后得到最优求解。之后加入拥挤度比较算子排序，使计算得到的解合理分布在 Pareto 解集中；再增加精英策略，保证种群进化的过程中，将原始种群中进行多次交叉变异，从而得到新的种群，并将适应度最高的新种群进行保存，提升收敛速度。

基于NSGA-Ⅱ算法的求解步骤：

3 结果与分析

为取得更好的实验效果，并验证本研究提出算法是否可行，本次实验将对不同的优化结果进行具体分析。

3.1 参数设置

NSGA-Ⅱ多目标优化算法设置

NSGA-Ⅱ多目标优化算法具体设置如表1所示。

表1 NSGA-Ⅱ多目标优化算法设置Tab.1 NSGA-Ⅱ multi-objective optimization algorithm settings

NSGA-Ⅱ参数设置

NSGA-Ⅱ参数具体设置如表2所示。

表2 NSGA-Ⅱ参数设置Tab.2 NSGA-Ⅱ parameter settings

3.2 优化结果

参数对优化过程和结果的影响

1)种群规模

具体分析种群规模对优化过程和结果的影响，结果如图1所示。交叉率和变异率分别设置为0.7和0.1。

图1 种群规模对优化过程和结果的影响Fig.1 Effect of population size on the optimization process and the results

由图1可知，当种群规模取值为4、10 和16时，种群的收敛速度明显减慢，种群多样性减少，最优解分布不均；当种群规模取值为28时，收敛速度加快，最优解得到均匀分布。

2)交叉率

具体分析交叉率参数设置对算法优化效果的影响，结果如图2所示。种群规模设置为28，变异率为0.1。

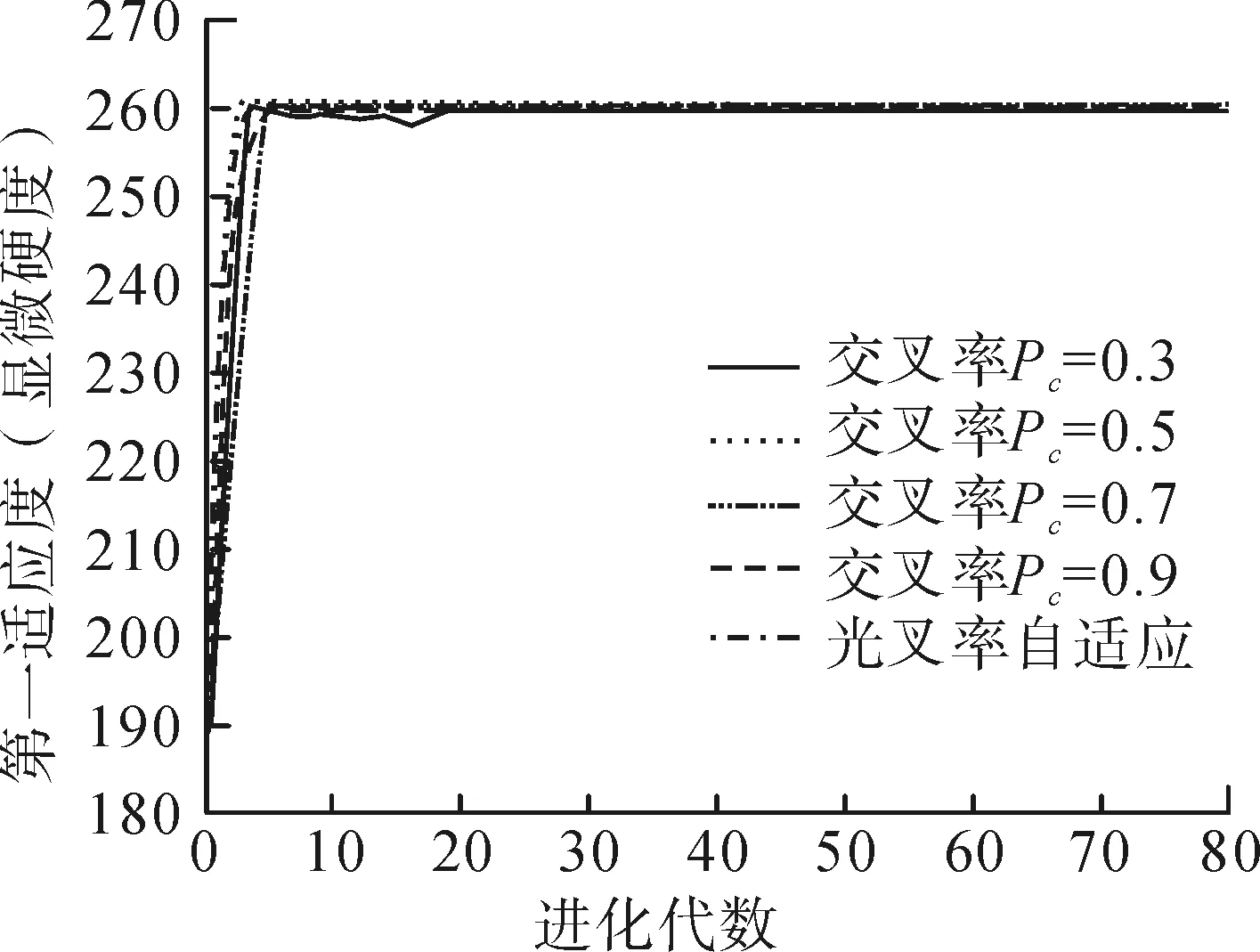
图2 交叉率对优化过程和结果的影响Fig.2 Effect of the crossover rate on the optimization process and the results

由图3可知，当交叉率为0.7、0.9时，种群收敛速度明显更快；交叉率在开始时缓慢收敛，但一段时间后开始快速收敛；说明交叉率的大小对优化结果的影响较小，当交叉率取值接近0.3或0.5时，解集分布不均。

3)变异率

具体分析不同变异率对适应度和种群解集的影响，结果如图3所示 。种群规模和交叉率分别设置为28和0.7。

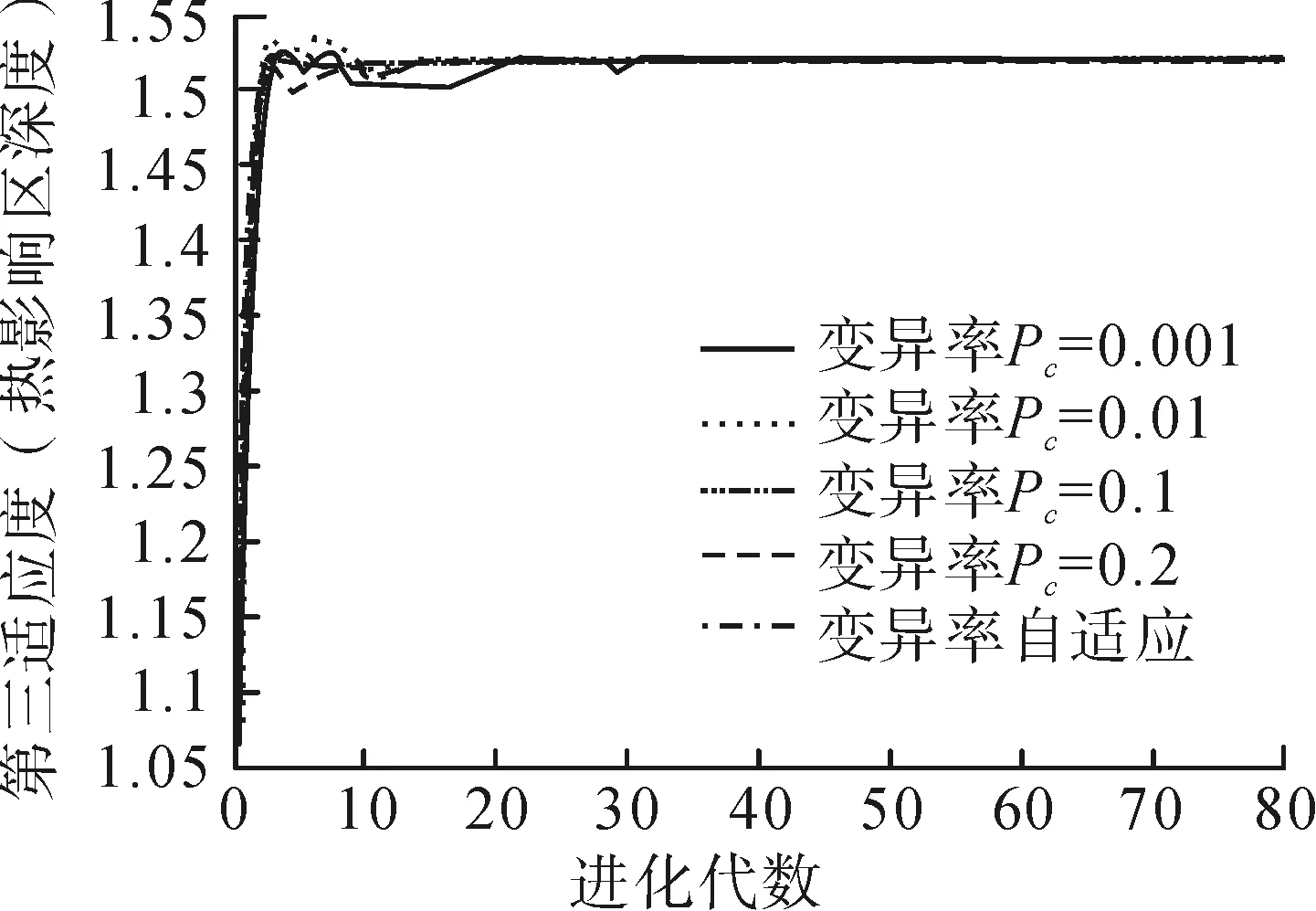
图3 变异率对优化过程和结果的影响Fig.3 Effect of the variation rate on the optimization process and the results

由图3可知，当变异率取值接近0.2时，算法-收敛速度较快，变异率开始时算法收敛速度较慢，一段时间后开始收敛速度明显加快；由此说明变异率的取值大小对优化结果的影响较小，当变异率取值靠近0.001～0.010时，算法优化效果不佳，解集分布不均。

NSGA-Ⅱ优化结果

进行上述优化结果分析后，得到最佳优化参数为：种群规模为28，交叉率为0.7，变异率为0.1；最后一代种群的解集如图4所示；选取253.58、0.07和0.49此3个解作为激光熔覆工艺参数 NSGA-Ⅱ多目标优化的最优解。

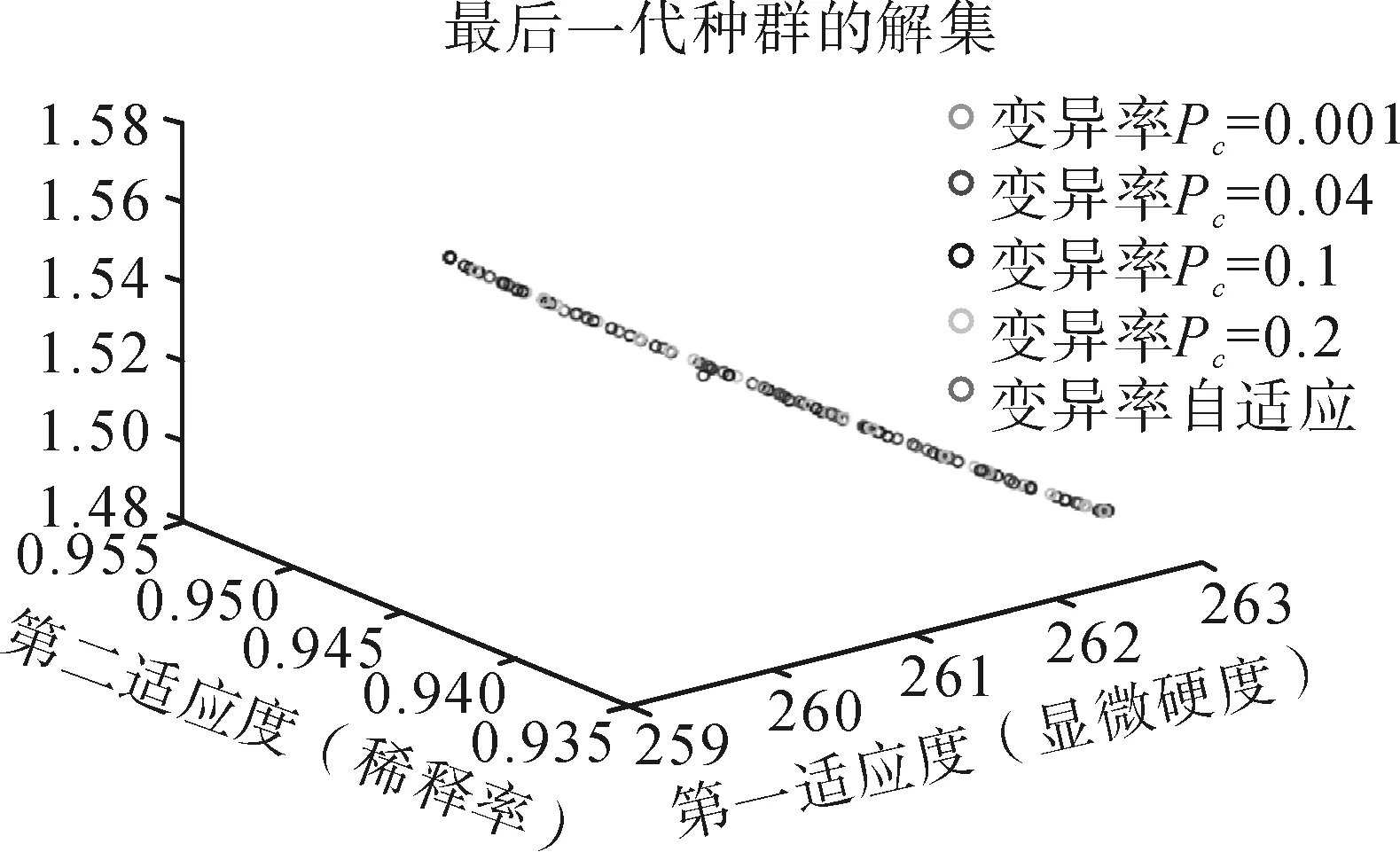
图4 NSGA-Ⅱ最终 Pareto 解集Fig.4 NSGA-Ⅱ final Pareto solution set

工艺参数多目标优化结果

1)不同优化方法结果对比

为验证本文提出的NSGA-Ⅱ算法的优化结果是否为最优结果，实验将本研究提出的 NSGA-Ⅱ方法与统一目标法的优化结果进行比较，得到的对比结果如表3所示。

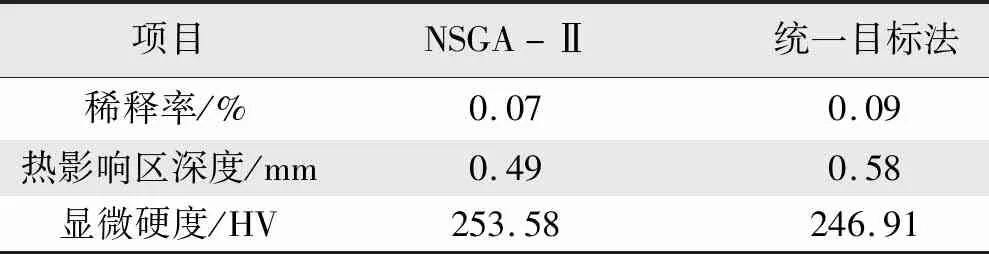
表3 2种算法优化结果对比Tab.3 Optimize the comparison of the results between the two algorithms

由表3可知，NSGA-Ⅱ优化结果显微硬度为253.58 HV，高出统一目标法6.67 HV；而稀释率和热影响区深度分别为0.07和0.49 mm，比统一目标法分别低了0.02、0.09 mm。由此可知，NSGA-Ⅱ比统一目标法的优化结果更好，算法性能更佳。

2)工艺参数优化前后的激光熔覆层性能对比

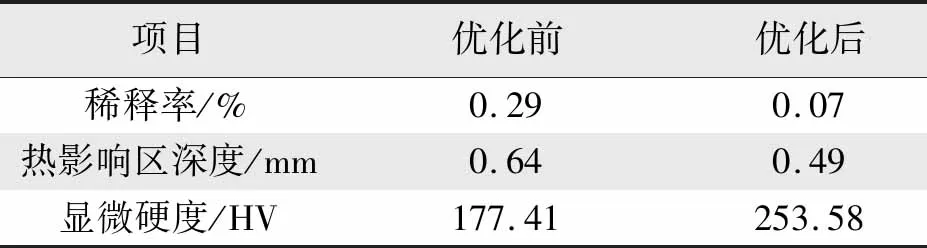
表4 优化前后激光熔覆层性能对比Tab.4 Performance comparison of laser fusion compound layers before and after the optimization

由表4可以看出，优化前和优化后的显微硬度分别为177.41和253.58 HV，优化后的显微硬度增加了42.93%；优化前后稀释率分别为0.29和0.07，优化后的稀释率降低了75.86%；优化前后热影响区深度分别为0.64和0.49 mm，优化后降低了2.43%。综合分析可知，优化后的激光熔覆层性能更佳。

4 结语

本研究提出的NSGA-Ⅱ多目标优化方法具备可行性和有效性。通过不同算法的参数设置后，最终取得了最优结果。实验结果表明：不同算法参数对NSGA-Ⅱ的优化过程和结果均有所不同，通过实验对比发现，相较于统一目标法，本研究提出算法优化效果更佳，优化后显微硬度高达253.58，稀释率和热影响区深度低至0.07和0.49，说明本研究优化后的激光熔覆层精度和质量有所提升，优化后算法性能更优越。但由于条件限制，本研究存在一定的局限性，主要表现在本研究只对NSGA-Ⅱ一种优化方法进行了研究，实验数据单一。因此，在未来的研究中，将重点在这方面进行改进，对更多的多目标优化方法进行深入探究，以得到更佳的优化结果。