基于K均值算法的分层教学模型研究

常凤　徐小华　胡忠旭　张子锋

摘要：由于学生群体存在个性化差异，传统教学模式已不能很好地满足学生全面发展的需求。而分层教学关注学生个体差异和学习需求，有针对性地制定教学计划和目标，有利于整体教学效果的提升。文章重点研究分层教学中的分层模型，并以计算机网络课程为例，设计基于K均值算法（K-means）的分层教学模型，实现学生学习情况的分层。通过仿真实验表明，基于K均值算法的分层教学模型相比专家分类算法、学生总成绩排名的分层方法，更具有一定科学性和合理性，可以为其他学科提供借鉴和参考。

关键词：分层教学模型;K均值;聚类;计算机网络

中图分类号：TP311      文献标识码：A

文章编号：1009-3044（2022）26-0054-03

1 引言

随着高等教育改革的推进，高等教育规模不断扩大，质量不断提高，高等教育的发展环境、使命担当和发展策略也发生了新的变化[1]。由于学生群体存在个体差异，进入大学后的目标也有很大的不同，在传统的教学模式下，教师需要通过大量的考试才能更准确地掌握学生的学习情况，这种方法已不能满足高校因材施教的教育原则及学生不同层次的学习需要[2]。传统“一刀切”的方式也容易造成基础水平高的学生觉得学习枯燥乏味，无法对知识进行深入学习和拓展研究，而基础水平低的学生因为基础薄弱而无法完成相应的任务，甚至有些学生平时非常努力，但因各种原因未掌握方法和技巧，所以考试失败，只能参加补考。久而久之，部分学生将对课程失去学习兴趣和信心。如何有效地面对全体学生，进行有效教学，激发学生学习兴趣和积极性，使存在个体差异的学生获得全面发展及个性发展，是教育教学面临的巨大挑战。

分层教学是教学改革的新方向，提供了教学的精准性。分层教学在一定程度上避免了“一刀切”的教学方法存在的弊端。分层教学依据学生现有的知识水平、学习能力以及学习潜力对学生进行分组，对于不同层次的学生，教师根据差异有针对性地调整教学方法和教学策略。根据分层教学理念，教师在课堂中重点关注较困难的学生，并挖掘出需要重点培养的对象，适应学生的全面发展需求。

传统的教学分层方法主要是从学生作业完成情况、学习成绩出发，依据数据的排列来将学生分成不同的层级，这种分层方法虽然高速直观，但忽视了知识构造的分层化。K均值算法（K-means）是一种迭代求解的无监督的聚类分析算法，算法简单易操作，执行效率高，可以有效地应用于学生学习行为的研究中。因此，本文采用K均值算法进行了分层教学模型的研究，并以计算机网络课程为例，探索通过分层次教学提高教学质量的教学方法。

2 分层教学

实施素质教育，培养新的人才实践能力和创新精神是当前高等教育改革与发展的基本目标，分层教学是素质教育的体现，是探索素质教育实施的新的教学方法[3]。分层教学落实对症下药、因材施教的教育理念，相对于原有的大一统思想和方案，分层教学改进和调整了教学方式方法，提高了教学效益，是实现因材施教和教学管理精细化的有效途径。据研究发现，分层次的教学方案是高校教育方式改革中最具有针对性的，具有较强的可操作性，并且具有普遍的运用价值与实践意义[4-5]。分层次教学遵循以人为本与因材施教的教育原则，具有能挖掘学生自身的学习潜能，能优化教学质量等优点[6-7]。

计算机网络课程是高校中计算机相关专业十分重要的必修课，具有较强的专业性和实践性。在实际教学中，学生课程基础、学习能力、学习态度等各不相同，若采取统一授课，则易造成“基础好的学生吃不饱，基础差的学生跟不上”的局面，容易造成课堂教学效率低下，不利于提高学生的学习兴趣，不适应高校教学的改革。根据计算机网络教学需求，文章提出一种基于K均值算法的分层教学模型，以此达到优化计算机网络教学目的，提高教学质量，满足不同学生对该门课程不同需求的目的。

3 K均值算法

4 K均值实现学生的分层

由以上的算法实现学生的分层有以下步骤：

1） 数据的收集

文章数据一共收集了400份的期末试卷，限于篇幅，文章只取了31个样本作为研究对象。研究的过程忽略了学生性别、考试时间、教学大纲和考试大纲、学时数等数据。

2） 数据整理

数据整理是将收集的试卷的进行合理、有效、科学的处理。按照分层教学的要求，分层不仅要考虑入学考试的总成绩，还应该包括学生每章节特别是重要章节的知识点得分率等，这样便可以了解学生对知识的掌握。通过归纳整理，试卷共有8个较重要知识点模块。分别用X1-X8表示，对应情况如下：X1网络体系结构;X2数据通信原理;X3数据链路协议;X4 IP地址划分及路由选择协议;X5 TCP协议及UDP协议;X 6局域网的设计与搭建;X 7无线局域网WLAN;X8 DNS域名系统。

3） 数据规范

数据规范是将数据标准化。在对成绩聚类分析时，需要将学生的所有章节或知识点的成绩和总成绩匹配成数值类型，进行规范化处理。

4） 数据分析

上述31个样本作为算法的初始数据。在分层前，初始凝聚点为三类，选择第1个、第14个、第25个样本观测值为初始凝聚点，然后进行分层分析，得到如图1的轮廓圖。

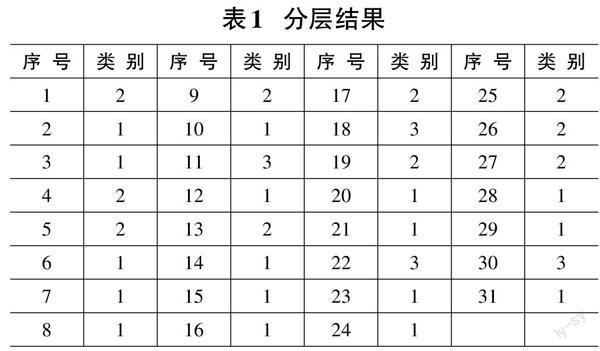
从轮廓图看出，将31个的观测数据分为3类，每个观测的轮廓值都大于零，并且都高于0.2以上，说明分为3类是非常合适的。其分层结果如表1所示。

从表中可以得到：第一类中学生有17人，总体表现优秀，该类学生在X1、X3、X7都表现较好，相对薄弱的模块为X5（TCP协议及UDP协议）。第二类有10人，该类学生总体表现一般，在X1、X2、X6和X7模块表现比较好，在其他模块表现较差。第三类有4人，总体表现较差，该类学生在X2、X3、X5、X6极其薄弱。有了这些分层信息，有利于教师调整授课重点，使教学更具有针对性，提高课堂教学效率。

5 分层算法比对

K均值聚类结果与专家聚类、学生总成绩排名对比如表2。从表中可以看出，K均值聚类与专家聚类有编号5、8、29不一致外，其余都相同。K均值聚类和成绩排名也有不相同，如序号为8的学生，成绩排名为18，但是从试卷答题来看，对重要知识点掌握很好，运算能力很强，但对基础题型掌握稍差，所以归为1类比较合理。从K均值聚类和专家分类、成绩排名对比来看，K均值聚类具有一定的科学性和合理性。

6 结束语

在实际教学中，分层教学实行差异化教学，树立“以学生为中心”的教学理念，实现分层定标、分层施教、分层练习、分层提高，能使教学更具有针对性，有利于教学效率的全面提高。文章以计算机网络课程为例，设计以K均值算法为基础的分层教学模型，相比专家分类算法、学生总成绩排名的分层方法，该模型分类准确，具有一定可移植性和推广性。

参考文献：

[1] 刘国瑞.新发展格局与高等教育高质量发展[J].清华大学教育研究，2021，42（1）：25-32.

[2] 唐佳诚，文欣秀，王家辉，等.用户画像分层教学模型研究[J].实验室研究与探索，2018，37（12）：196-200.

[3] 李惠.分层次教学在高等教育中的探讨[J].亚太教育，2016（3）：63.

[4] 曾亮.基于聚类分析方法的高职高等数学分层教学的新探索[J].职业时空，2010，6（11）：58-60.

[5] 程树林.高职院校《高等数学》分层教学方法的探讨[J].产业与科技论坛，2011，10（2）：168-169.

[6] Han T Y，Wen J J.Normal Distribution and Associated Teaching Efficiency[J].Mathematics in Practice and Theory，2014（6）：183-193.

[7] 刘珊，亓健.基于K-means聚类的高等数学分层教学模型[J].科技通报，2016，32（1）：230-233.

[8] 崔雪征.基于改进K均值算法的医保就医行为研究[J].现代科学仪器，2021（6）：229-232.

[9] 张艳丽，张守祥.Hilbert-Huang变换在声振信号检测钢管混凝土脱空中的应用[J].煤炭学报，2010（1）：165-168.

【通联编辑：谢媛媛】

收稿日期：2022-04-19

作者简介：常凤（1989—） ，女，云南昭通人，助教，硕士，主要研究方向為算法理论、计算机应用;徐小华（1980—） ，男，四川南充人，副教授，硕士，主要研究方向为算法理论;胡忠旭（1983—） ，男，云南昭通人，通信作者，副教授，学士，主要研究方向为软件开发技术;张子锋（1985—） ，男，河南信阳人，讲师，硕士，主要研究方向为数据结构。