考虑火花效应的杆塔接地体冲击接地电阻仿真计算

杨秋玉，郑小刚

(福建工程学院电子电气与物理学院，福州 350118)

0 引言

良好的接地是保证线路及电站可靠运行、保障电气设备与运行人员安全的重要条件[1-4]。接地装置在雷电流作用下的接地电阻称为冲击接地电阻，由于电感效应和火花放电效应，冲击接地电阻与工频接地电阻相差较大，冲击接地电阻是衡量线路防雷性能的重要指标。如果杆塔接地装置冲击接地电阻过高，将造成接地装置及周围电位异常升高、塔顶电压过大，导致绝缘子闪络、线路跳闸等事故的发生。因此，准确分析接地装置在雷电流作用下的冲击特性对杆塔的雷电防护至关重要。

国内外针对接地体冲击接地电阻的计算问题开展了大量的研究，取得了一定的成果。根据计算原理，主要有基于电路理论[5-8]、基于传输线理论[9-12]和基于电磁场理论[13-16]的冲击接地电阻计算方法。其中，基于电路理论的计算方法将接地导体等效为由多段π型等值电路，计算模型简单，且能够模拟土壤非线性过程。文献[17]利用PSCAD电磁暂态模拟软件建立了考虑火花效应的水平接地电极π型等值电路模型，仿真分析了接地电极长度及接地电极土壤电阻率对冲击接地电阻的影响。文献[18]则采用ATP-EMTP电磁暂态分析软件搭建单根伸长水平接地体的π型等值电路模型，该模型考虑了火花效应的影响，利用该模型计算了接地体电阻随时间、接地体长度、雷电流、土壤电阻率的变化情况。然而，现有的基于电路理论的冲击接地电阻计算方法缺乏考虑火花放电区域的修正，使得计算得到的冲击接地电阻与实际相比存在一定的误差。

笔者采用接地体等效半径迭代法建立考虑火花放电效应的接地体等效模型，该模型能较好地反应接地体在雷电流作用下的电感效应和火花放电效应，仿真计算得到的接地体冲击电流下的接地阻抗更接近实际情况。

1 土壤击穿机理

土壤是一种包含固体、液体和气体的复杂混合物。固体成分主要由各种矿物质、有机质等组成；在土壤的孔隙中，存在着水分和空气。一般地，矿物质和有机质分别占土壤体积分数的45%和5%，水分占20%～30%，空气占20%～30%。正是由于土壤复杂的结构，当有雷电流注入时，会发生复杂的放电和散流现象。

由于雷电流波头极陡，是一种高频的冲击波，使得呈感性阻抗的接地体阻止雷电流中的高频分量向接地体远处传播，长接地体不能得到有效利用，导致接地体的冲击接地电阻高于工频接地电阻，雷电流的这一特点称为电感效应。此外，由于雷电流幅值极高，当幅值极高的雷电流不能沿接地体长距离传播时，将导致接地体与土壤之间的电流密度和电场强度剧增，当电场强度超过土壤临界击穿场强时土壤被击穿，此时的接地电阻小于工频接地电阻，这一特点称为火花放电效应。

当雷击杆塔时，雷电流经杆塔、接地装置流散至大地。在雷电流的作用下，接地装置周围产生的电场强度为[19]

E=ρ·J

(1)

式中，ρ为土壤电阻率，J为电流密度。由该式可知，随着冲击电流幅值的增加，电场强度不断增大，靠近接地体土壤的电场强度如果超过土壤的临界击穿场强，则土壤开始被击穿。图1为一水平接地极周围土壤发生局部放电示意图，从内至外可分为4个区域，分别为电弧区、火花区、电解质传导区和恒定电导区。电弧区的电流密度最大，具有明显的放电通道，该区域的电压降可忽略不计；火花区的电流密度较电弧区的有所减小，该区域中的单个火花通道直径较小，但由于火花数量较多，该区域的电压降也可忽略不计；随着电流继续向外扩散，电流密度所产生的电场强度小于土壤临界场强，土壤已不能被击穿，但对土壤所呈现的电导值有影响，因此称该区域为电解质传导区；当电流继续向外扩散，电流密度较小，土壤电导不再受影响，该区域为恒定电导区。

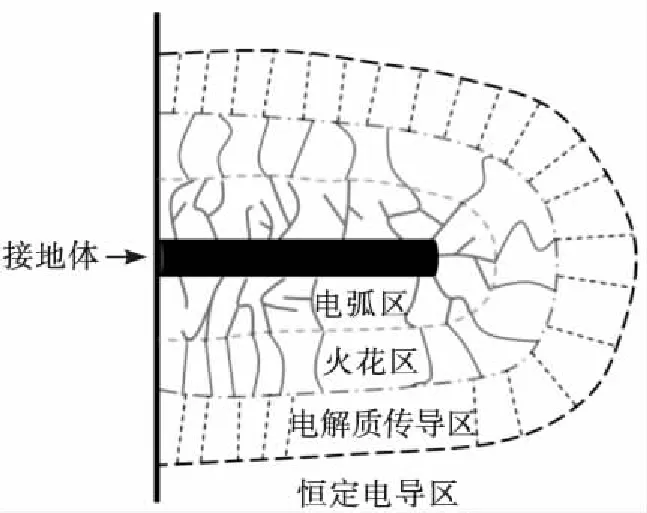
图1 土壤放电示意图

由此可知，当土壤被击穿后，土壤的电导率大幅增大，散流性得到改善，相当于可以把被击穿的土壤区域看作是增大了接地极的直径。

另外，由于雷电流的特点以及接地体自身阻抗的原因，接地体各处散流并不均匀，

越到接地体末端电流和电压衰减越大，因此，沿接地体长度方向的火花放电程度也不同，火花放电效应是一个非线性的过程[20-23]。为了仿真计算的方便，可以将接地体进行分段处理，将接地体等效为若干段包含火花放电区域的圆柱体组合，见图2。

图2 接地体附近土壤火花放电区域的物理模型

图2中各段接地体的等效半径为[24]

(2)

式中：ρ为土壤电阻率，ΔIi为流过第i段接地体的电流，li为每段接地体的长度，Ec为土壤的临界击穿场强，可按式(3)进行计算[25]。

Ec=241ρ0.215

(3)

2 考虑火花放电效应时接地体的等效模型

将接地体人为分成若干段，每一小段可以看成是由自电阻R、自电感L、对地电容C和对地电导G组成的π型等值电路[26]，见图3。

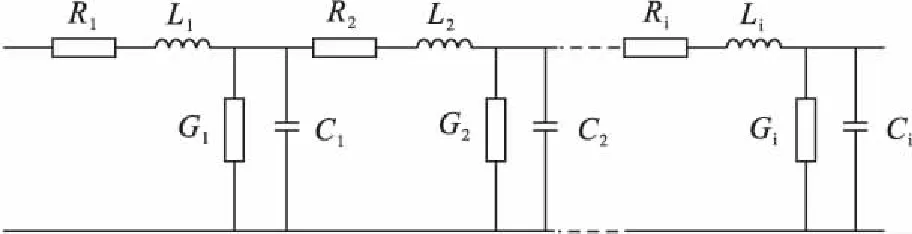
图3 水平接地体等值电路

图3中各参数可按式(4)-(7)计算得到：

1)接地体自电阻Ri

(4)

式中：ρ0为接地体电阻率；li为第i段接地体长度；S=πr2为接地体横截面积，r为接地体半径。

2)接地体自电感Li

(5)

式中：μ0为真空磁导率，μ0=4π×10-7H/m。

3)接地体对地电导Gi

(6)

式中：ρ为土壤电阻率；h为接地体埋深。

4)接地体对地电容Ci

Ci=ερGi

(7)

式中：ε为土壤介电常数，一般取ε=9×8.86×10-12F/m。

3 算例分析

按照第1、2节所述的原理，笔者以一水平接地体为算例，验证采用修正迭代接地体等效半径的方式模拟火花放电效应对接地体冲击接地电阻的影响。

假设接地体为长l=24 m、半径r=5 mm、电阻率ρ0=0.13 Ω·mm2/m的圆钢，接地体水平埋深h=0.6 m，土壤电阻率ρ=120 Ω·m，雷电流波形为2.6/50 μs、幅值为20 kA。

首先对接地体进行分段处理，每6 m为一段；再建立各段的π型等值电路，电路元件参数根据式(4)-(7)进行计算；最后将各段等值电路串联起来，即为接地体的电路模型，模型参数计算结果如下：

R1=R2=R3=R4=0.009 9 Ω

L1=L2=L3=L4=8.14×10-6H

G1=G2=G3=G4=0.039 S

C1=C2=C3=C4=3.73×10-10F

利用ATP-EMTP软件，按照上述初始参数建立电路模型见图4。

图4 24 m水平接地体仿真模型

选择Heidler冲击电流源模拟波形为2.6/50 μs、幅值为20 kA的雷电流，见图5。

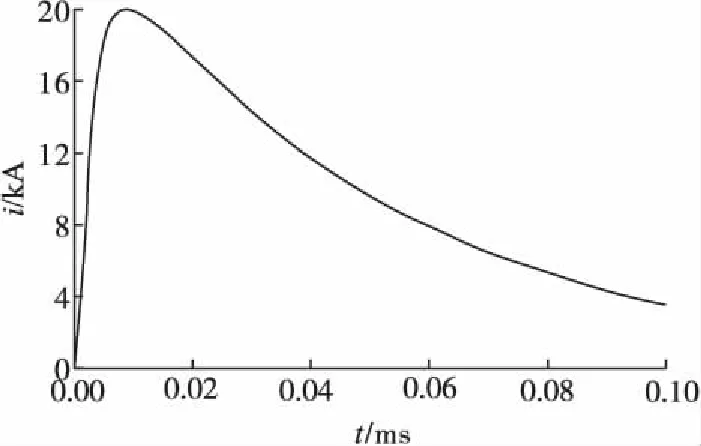
图5 仿真用雷电流波形图

3.1 不考虑火花放电效应的仿真结果

水平接地体雷电流入地端(接地体首端)电流电压波形见图6。

图6 水平接地体首端电流电压波形

各分段接地体的散流电流波形见图7。

图7 各分段接地体散流电流波形

各分段接地体的散流变化情况见图8。

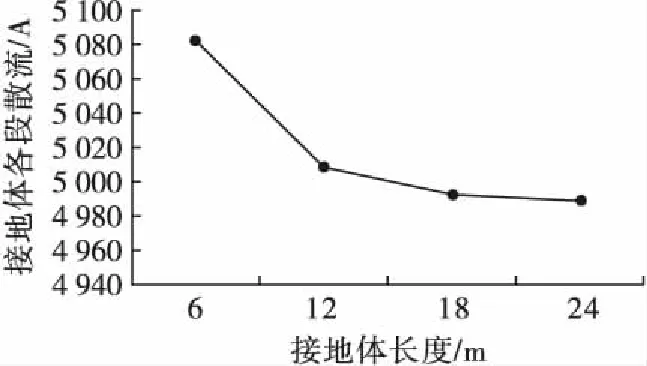
图8 各分段接地体散流变化情况

3.2 考虑火花放电效应的仿真结果

根据图8所示的各段接地体散流计算结果，带入式(2)，得到各段接地体的等效半径，再由式(6)、(7)计算接地体对地电导和对地电容。根据这些参数，对原模型进行修改更新。土壤临界击穿场强由式(3)计算可得Ec=674.59 kV/m。

第1次迭代修正结果见表1。

表1 第1次迭代修正结果

修正后的水平接地体雷电流入地端(接地体首端)电流与电压波形见图9。

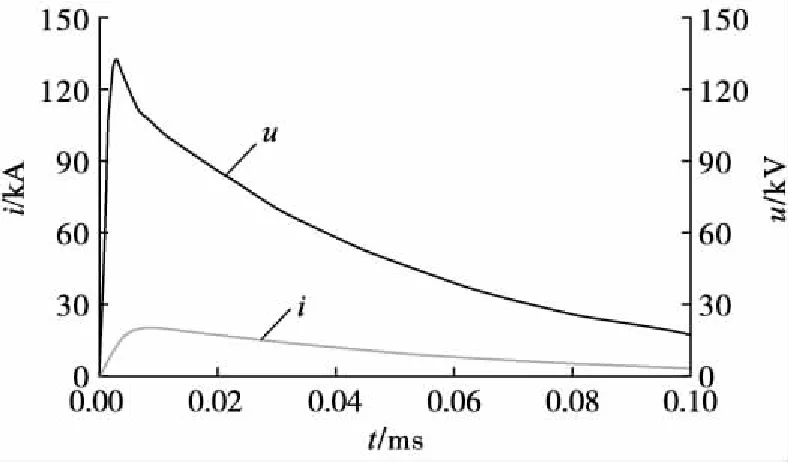
图9 修正后的水平接地体首端电流与电压波形

各分段接地体的散流电流波形图见10。

图10 各分段接地体散流电流波形

各分段接地体的散流变化情况见图11。

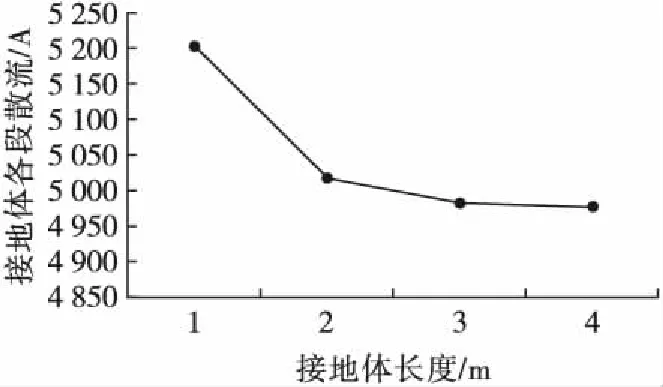
图11 各分段接地体散流变化情况

根据上述结果，进行第2次修正迭代，结果见表2。

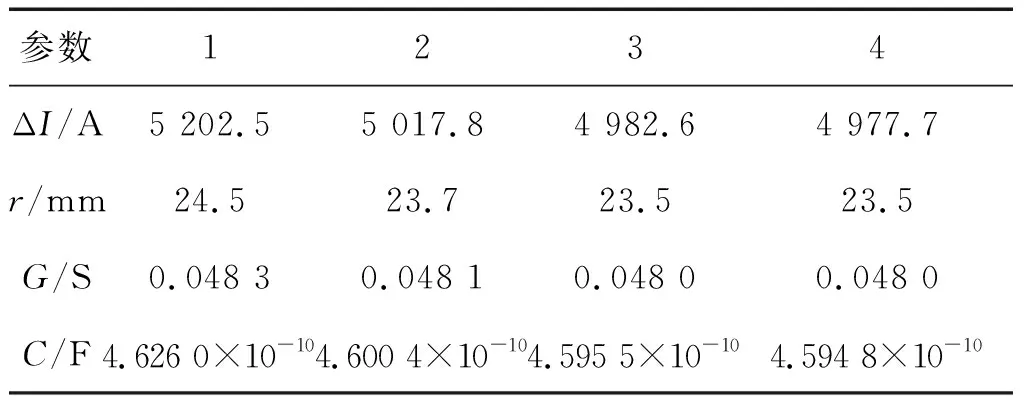
表2 第2次迭代修正结果

修正后的水平接地体雷电流入地端(接地体首端)电流电压波形图见12。

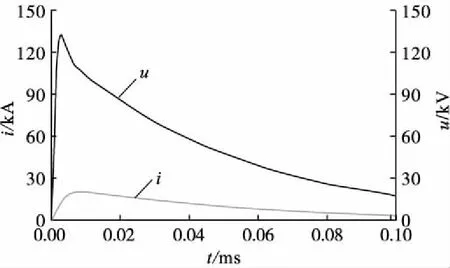
图12 修正后的水平接地体首端电流电压波形

各分段接地体的散流电流波形图见13。

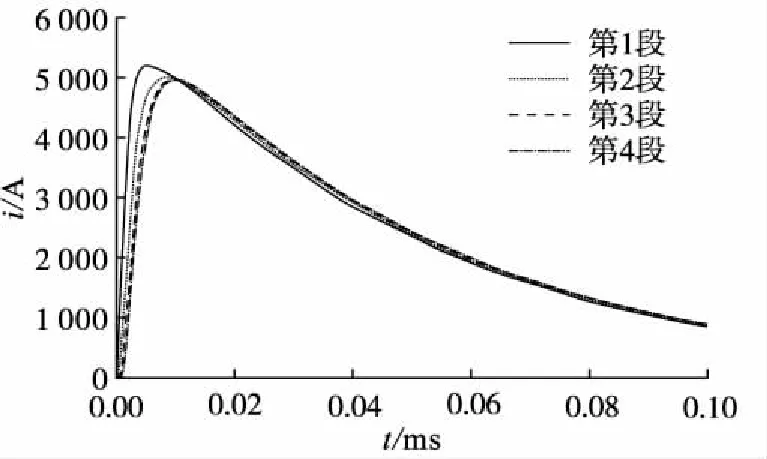
图13 各分段接地体散流电流波形

各分段接地体的散流变化情况见图14。

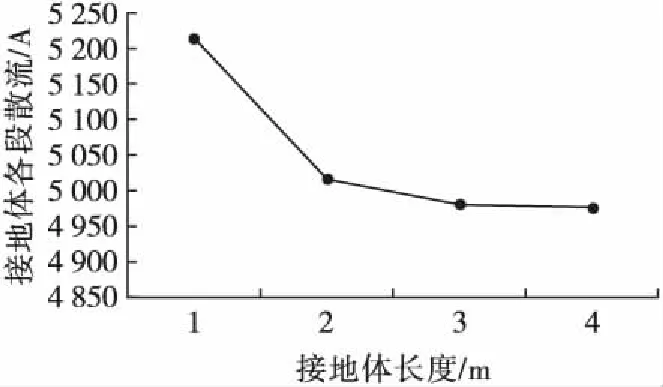
图14 各分段接地体散流变化情况

经过以上两次迭代修正后，从表1、表2中可以看出，接地体的等效半径ri变化已经很小，因此可以认为经过两次迭代修正后的模型为最终考虑火花放电效应的模型，根据该模型计算冲击接地电阻：

如果依据未考虑火花效应的原始模型，计算的冲击接地电阻为

由此可以看出，考虑火花效应前后冲击接地电阻变化率为12.29%。因此，本研究所提出的仿真计算方法能够更准确地反映实际情况下杆塔接地体的冲击接地电阻。

4 结论

1)建立了考虑火花效应的接地体等值电路模型，模型通过迭代修正法对接地体等效半径进行修正，使得冲击接地电阻计算更准确。

2)由于火花放电区域电导率大大增加，因此可以将该区域等值为接地体的等效半径；由于火花放电区域沿接地体由近到远呈圆锥递减分布，因此可将接地体分成若干小段，每一小段用集中参数近似处理。

3)通过对一接地体在波形为2.6/50 μs、幅值为20 kA的雷电流冲击下进行仿真分析，得到的冲击接地电阻相比未考虑火花效应时的模型相差12.29%，更接近实际值。