乏燃料后处理厂核材料衡算仿真

步立新，何丽霞，刘宏斌

(中国原子能科学研究院，北京 102413)

乏燃料后处理厂是处理反应堆辐照后的乏燃料并提取其中铀钚以及其他锕系元素的重要设施，其特点是年处理量大、工艺流程复杂、物料形态多样，其中的核材料衡算面临很大挑战，同时重要核材料“一克不少、一件不丢”是我国核材料衡算的目标。乏燃料后处理厂属于散料核设施，由于核材料测量设备存在测量不确定度，即使不存在核材料损失，核材料的不平衡差(MUF)也不等于零。从统计学分析，如果能够确定MUF值处于测量不确定度误差范围内(通常在95%置信度下取2σMUF)，可以认为衡算周期内MUF主要来源于测量系统的误差，后处理核材料衡算实现了闭合。另一方面核设施的总不确定度必须满足国家法规要求，否则过大的测量不确定度会导致置信区间过于宽泛，测量误差掩盖了真实存在的不明材料量流失而使评价结果失去意义。国家法规要求铀钚闭合平衡结算的MUF不确定度σMUF分别小于核材料通过量的0.8%和1.0%[1]。

针对核材料衡算许多文献进行了讨论，王宏军[2]讨论了散料核设施MUF评价的概率统计方法；高雪梅[3]在讨论MUF及σMUF计算的同时分析了国内核材料衡算存在的问题;杨英[4]对后处理厂的调试铀进行了衡算研究，发现核材料衡算不能闭合的主要原因是MUF较大；张敏[5]总结了后处理厂中核材料衡算的问题；陈云清[6]针对后处理厂的一个核材料平衡区选定了若干关键测量点，利用误差模型对后处理厂的MUF相对标准偏差进行了计算和评价。仿真是研究后处理的新方法，Cipiti[7-10]采用Simulink工具软件构建了后处理厂的过程监控仿真模型并实现对核材料衡算模拟，Cipiti在文献[11-12]中介绍了在后处理厂设计阶段衡算仿真模型的应用。Shugart[13-14]也采用Simulink软件建立了以核材料平衡区为基础衡算仿真模型，并通过不同的统计测试方法来验证系统是否出现核材料流失。Lixin Bu[15]通过软件算法直接构建后处理模型实现了后处理厂近实时衡算仿真。

仿真是一个将现实复杂系统的运作规律利用计算机有选择、有针对性地在计算机内表达出来，并通过有目的的计算改善外部世界的有效手段。仿真模型与所研究系统的运行过程在形式上和逻辑上存在对应性，避免了建立抽象数学模型的困难，可以显著简化建模过程。本研究开展后处理衡算仿真研究，结合工艺流程综合分析研究相关参数变化导致的核材料衡算结果的变化，对不同规模的衡算系统进行评价，进而优化测量系统不确定度目标值的合理分配，以及为核材料闭合衡算的评价和工艺过程监控提供支持。

1 后处理仿真建模

建立后处理过程仿真计算模型需要将后处理过程以数学方式表达出来，首先把后处理过程分解成多个单元，如剪切溶解单元、1AF供料计量单元、1AF萃取单元，以及其他萃取单元等。

剪切溶解单元可以简化为一个溶解过程，令U0为乏燃料中未溶解铀质量，s1为铀的溶解速率，dU是单位时间铀的溶解量，Ur是铀的累计溶解量，则公式(1)表示铀的溶解过程：

dU=U0*s1

Ur=Ur+dU

U0=U0-dU

(1)

同理，令Pu0为乏燃料中未溶解钚质量，s2为钚的溶解速率，dPu是单位时间钚的溶解量，Pur是钚的累计溶解量，则公式(2)表示钚的溶解过程：

dPu=Pu0*s2

Pur=Pur+dPu

Pu0=Pu0-dPu

(2)

1AF供料计量单元是一个包含测量误差的随机过程，令Us和Pus分别是铀钚的测量值，U和Pu是铀钚质量的真值，δ1r和δ2r是铀钚测量的相对随机误差，δ1s和δ2s是铀钚测量的相对系统误差，则1AF的测量可以表示为公式(3)：

Us=U(1+X1r+δ1s)

Pus=Pu(1+X2r+δ2s)

(3)

其中，X1r是以零为均值，铀测量相对随机误差δ1r为标准差的正态分布的随机变量；X2r是以零为均值，Pu测量相对随机误差δ2r为标准差的正态分布的随机变量。仿真计算可以得到一个包含随机量的测量值，最后计算得到相应的MUF值也是一个包含随机误差和系统误差的具有MUF特征的随机值。

萃取单元可以简化为一个铀钚元素逐渐分离的过程。令p1和p2分别为萃取器单位长度U和Pu的萃取率，U0为进入萃取器的初始U量，U1为萃取器中第二段中的U量，U2为萃取器中第三段中的U量，同样，Pu0为进入萃取器的初始Pu量，Pu1为萃取器中第二段中的Pu量，Pu2为萃取器中第三段中的Pu量，则萃取器中的萃取过程可以表示为公式(4)：

U1=U0*p1

U2=U1*p1

U3=U2*p1

U4=U3*p1

………

Pu1=Pu0*p2

Pu2=Pu1*p2

Pu3=Pu2*p2

Pu4=Pu3*p2

………

(4)

将这些计算过程根据后处理流程以图1方式串联得到后处理过程仿真，其中根据后处理流程将核材料分为4个衡算平衡区。

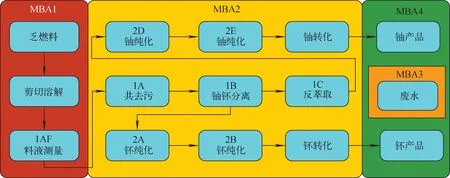
图1 后处理流程框图

2 仿真核材料衡算计算[1]

仿真模型中核材料衡算是以核材料平衡区为基础，按公式(5)确定衡算周期内每个核材料平衡区的不平衡差(material unaccounted for, MUF)：

MUF=PB+X-Y-PE

(5)

在核材料定期盘存(PIT)时，后处理工艺停车并进行盘存测量得到期初(PB)与期末(PE)后处理系统中的核材料存量，X和Y分别是整个盘存周期内流入和流出的材料量。

在仿真模型中，MBA2的PB和PE都是0，X是1AF进料测量点，Y是铀产品和钚产品的测量点，以及废水测量点。

评估MUF采用置信区间法求MUF真值的置信区间，计算置信区间下限L和置信区间上限U通常采用2σ(MUF)的置信区间，即：

U=MUF+2σ(MUF)

(6)

L=MUF-2σ(MUF)

(7)

当L<0

MUF的测量方差σ2(MUF)的计算公式如下：

(8)

MUF的相对标准偏差计算公式如下：

(9)

式中：δ(MUF)是MUF的相对标准偏差，T是平衡周期内材料的通过量。

3 仿真模型计算与分析

假设有200个乏燃料组件准备进行处理，每个组件含铀400 kg，U、Pu和裂变碎片的含量分别是98%、1%和1%。乏燃料溶解时间设置为24 h，设施需要约200 d完成后处理并进行MUF计算。每个测量点的铀钚测量相对误差分别列于表1。

采用假设生产工况及衡算测量点测量不确定度(表1)进行仿真计算，得到相应生产流程的核材料衡算数据，根据MUF方差公式计算对应环节的MUF方差值。在实际生产中MBA1的乏燃料中铀钚的量是通过估算得到，其测量不确定度较大，收发差也存在很大的不确定度，在该平衡区进行衡算意义不大，除非开发出对乏燃料测量不确定度较小的方法。MBA3和MBA4是核材料的存储区，不存在核材料形态变化，因而未包含在仿真模型中，MBA2是后处理的核材料衡算研究的重点。

表1 铀、钚元素各测量点的随机误差与系统误差值

3.1 MBA2的Pu定期衡算的MUF方差组成

经过后处理衡算仿真模型计算，MBA2的Pu衡算在国际目标值条件下和假设测量不确定度条件下，各环节误差方差对整体MUF方差的贡献示于图2。由图2a可知，国际目标值条件下，1AF中Pu含量测量的系统误差的方差占整体MUF方差的90%以上。由图2b可知，采用假设测量不确定度，1AF的Pu含量测量的系统误差方差也占整体MUF方差的50%以上，其次是1AF的体积测量系统误差方差和Pu产品总体测量的系统误差方差，而相应测量的随机误差方差由于多次测量的平均效应对整体MUF方差的贡献较小，其中1AF的Pu含量测量随机误差方差在两种条件下约占系统MUF方差的1%，而两种条件下整体MUF相对标准偏差δPu(MUF)分别是0.51%和0.77%，均小于法规要求的1.0%[1]。

图2 国际目标值(a)和假设测量不确定度(b)条件下MBA2中Pu的方差构成分布

3.1.11AF中Pu测量误差对总误差的变化趋势 分别改变1AF中Pu测量的随机误差Pu1AF(r)和系统误差Pu1AF(s)，得到相应条件下对系统相对标准偏差δPu(MUF)的影响(图3a)，其中δPu(MUF)随系统误差的增长较相对随机误差快，对系统相对标准偏差δPu(MUF)起主要作用。改变1AF体积测量的随机误差T1AF(r)和系统误差T1AF(s)，可以得到其对系统相对标准偏差δPu(MUF)的影响(图3b)，其中系统误差相对随机误差影响大，对系统相对标准偏差δPu(MUF)起主要作用。

图3 1AF中Pu测量误差与系统不确定度δPu(MUF)的关系

3.1.2Pu产品测量误差对总误差的变化趋势

改变Pu产品中Pu含量测量的随机误差PuProduct(r)和系统误差PuProduct(s)，得到其对系统相对标准偏差δPu(MUF)的影响(图4a)，其中系统误差相对随机误差对系统相对标准偏差δPu(MUF)起主要作用。改变Pu产品称重测量的随机误差TProduct(r)和系统误差TProduct(s)，可以得到相应不确定度对系统相对标准偏差δPu(MUF)的影响(图4b)，其中系统误差相对随机误差对系统相对标准偏差起主要作用。

图4 Pu产品中测量误差与系统不确定度δPu(MUF)的关系

3.1.3废液测量误差对总误差的变化趋势 改变废液中Pu含量测量的随机误差Puwaste(r)和系统误差Puwaste(s)，得到相应不确定度对系统相对标准偏差δPu(MUF)的影响(图5a)，由于废液中Pu含量极低，Pu含量测量的随机误差和系统误差对δPu(MUF)的贡献都很小，随机误差和系统误差达到30%，对系统相对标准偏差δPu(MUF)影响不大。改变废液体积测量的随机误差Twaste(r)和系统误差Twaste(s)，得到相应不确定度对系统相对标准偏差δPu(MUF)的影响(图5b)，由于废液中Pu含量极低，废液体积测量的随机误差和系统误差达到20%，对系统相对标准偏差δPu(MUF)几乎没有影响。

图5 废液中Pu测量误差与的δPu(MUF)的关系

3.2 MBA2的U定期衡算的MUF方差组成

根据相同模型计算MBA2中U衡算的MUF方差分布，U衡算在国际目标值条件下和假设测量误差条件下各环节误差方差对整体MUF方差的贡献示于图6。国际目标值条件下，1AF的U含量测量的系统误差方差占整体MUF方差的50%以上(图6a)，适度放大其他环节不确定度后(图6b)，1AF的U含量测量的系统误差方差也占整体MUF方差的40%以上，其次是U产品的含量测量系统误差方差和U产品称重测量的系统误差方差，而相应测量的随机误差方差由于多次测量的平均效应对整体MUF方差的贡献较小，其中1AF的U含量测量随机误差方差在两种条件下约占整体系统MUF方差的1%，而两种条件下整体MUF相对标准偏差δU(MUF)分别是0.26%和0.64%，均小于法规要求的0.8%[1]。

图6 国际目标值(a)和假设测量不确定度(b)条件下MBA2中U的方差构成分布

3.2.11AF中U测量误差对总误差的变化趋势 改变1AF中U含量测量的随机误差U1AF(r)和系统误差U1AF(s)，得到对整体MUF相对标准偏差δU(MUF)的影响(图7a)，其中系统误差相对随机误差影响大，对δU(MUF)起主要作用。改变1AF体积测量的随机误差T1AF(r)和系统误差T1AF(s)，得到对δU(MUF)的影响(图7b)，其中系统误差相对随机误差影响大，对δU(MUF)起主要作用。

图7 1AF中U测量误差与系统不确定度δU(MUF)的关系

3.2.2U产品中U含量测量误差对总误差的变化趋势 改变U产品中U含量测量的随机误差UProduct(r)和系统误差UProduct(s)，得到其对δU(MUF)的影响(图8a)，其中系统误差相对随机误差影响大，对δU(MUF)起主要作用。改变U产品称重测量的随机误差TProduct(r)和系统误差TProduct(s)，得到相应不确定度对δU(MUF)的影响(图8b)，其中系统误差相对随机误差影响大，对δU(MUF)起主要作用。

图8 U产品测量误差与系统不确定度δU(MUF)的关系

3.2.3废液中U含量测量误差对总误差的变化趋势 改变废液中U含量测量的随机误差Uwaste(r)和系统误差Uwaste(s)，得到其对δU(MUF)的影响(图9a)，由于废液中U含量很低，U含量测量的随机误差和系统误差对δU(MUF)的贡献都很小，随机误差对δU(MUF)几乎无影响，系统误差达到10%对δU(MUF)影响不大。改变废液体积测量的随机误差Twaste(r)和系统误差Twaste(s)，可以得到相应不确定度对δU(MUF)的影响(图9b)，由于废液中U含量比较低，废液体积测量的随机误差和系统误差对δU(MUF)的贡献都不大，随机误差和系统误差达到5%对δU(MUF)几乎没有影响。

图9 废液中U测量误差与的δU(MUF)的关系

3.3 数据分析

分析计算数据可以得到以下规律。

1)所有关键测量点的系统误差相比对应的随机误差对整体MUF的相对标准偏差δ(MUF)的影响更大。这是由于经过多次测量，随机误差被逐渐平均化，假设Ti是单次测量值，δ是测量的相对随机误差，Tiδ是单次测量随机误差，则多次测量后的相对随机误差是：

(10)

若T1=T2=T3=…=Tn，则

(11)

2)在所有条件下1AF的U、Pu含量测量的系统误差对系统MUF误差方差的占比都超过了40%，是系统不确定度的主要来源，特别是1AF中Pu的含量低，测量不确定大，占比系统不确定度系统误差方差超过50%，因此改善MUF不确定度的最优方向是减小1AF铀钚含量测量的系统误差。1AF的体积测量相比含量测量精度较高，对系统不确定度的影响小于1%。

3)通常情况下废水中U、Pu含量很少，对其测量的不确定度为10%时，对整体MUF相对标准偏差δ(MUF)的影响小于1%。

4 结论

本模型中采用的包括生产规模及核材料测量误差的数据是参考标准模型的假设值，通过仿真模型计算得到具有参考意义的核材料衡算结果，验证了仿真方法的有效性。当把真实后处理厂的核材料衡算参数输入仿真模型中可以得到相应的计算结果，对于实际后处理厂中出现的核材料衡算问题具有指导意义，同时也可以为我国后处理厂核材料衡算的改进提供参考。