基于蒙特卡洛方法的瞬变电磁接收机过渡过程研究

王广君，段雪影，黄鲸珲，胡祥云

(1.中国地质大学 自动化学院，湖北 武汉 430074；2.中国地质大学 复杂系统先进控制与智能自动化湖北省重点实验室，湖北 武汉 430074；3.中国地质大学 地球物理与空间信息学院，湖北 武汉 430074；4.中国地质大学 地质过程与矿产资源国家重点实验室，湖北 武汉 430074)

1 引 言

瞬变电磁法是一种高效率、无损、低成本的物探方法。通常通过发射机发射一个脉冲信号激励地下地质体产生二次场，然后对接收机测得的感应电压进行反演从而得到地下介质的信息。瞬变电磁法自1956年Wait[1]提出以来已经成为了地表地质调查中[2]最重要的方法。例如对铜、钼、铅锌、铝土矿、铀等金属资源的勘察[3]；对岩土工程勘察中的采空区(空洞)、含水构造、土石分界及岩层富水情况进行地球物理勘查[4]。近年来，由于城市的快速发展，浅层地质结构的探测与成像在城市地下空间利用、防灾减灾等方面的作用越来越重要，城市地下空间的地质构造的精确勘察可以有效地避免地质灾害和巨大的经济损失[5-7]。

传统瞬变电磁法的浅层探测能力受限于发射机的关断时间和接收机的过渡过程[8,9]。由于发射机的关断时间不为零，在早期会激发一次场，导致探测到的早期信号是一次场和二次场叠加的总场。此外，非零关断的磁场响应与理想关断的磁场响应之间存在差异，导致后期计算视电阻率存在误差，从而影响瞬变电磁法浅层探测中对二次场的反演解释精度[10]。为此，孙天财等推导了斜阶跃场源激励下的瞬变响应解析式，并提出了一种不需要进行关断效应校正直接计算全程视电阻率的方法，可减小视电阻率的误差[11]。中南大学席振铢教授于2016年提出了等值反磁通瞬变电磁法[12]，可以有效地剔除一次场的影响，该方法采用上下平行共轴两组相同线圈为发射源，从而保证在该双线圈合成的一次场零磁通平面上一次场的大小为零。在此基础上，周超等提出了一种将等值反磁通瞬变电磁法和微动法联合起来的联合方法，为城市地下空间调查工作提供了一种行之有效的物探组合手段[13]。史存焕等提出了一种共轴偶极的瞬变电磁装置方法，可减小多匝线圈的互感效应[14]。但是目前对于瞬变电磁系统中的过渡过程还没有充分的研究，在传统的瞬变电磁法的浅层探测中，通常通过延时接收的方案来减小过渡过程对信号造成的畸变，但是这样会造成浅层探测的盲区。此外，接收线圈的大小和匝数也会对过渡过程造成影响[15]，所以有必要对瞬变电磁系统中的过渡过程进行进一步的研究。

本研究基于Simulink对瞬变电磁接收机的过渡过程进行建模分析，通过与自制的瞬变电磁系统“WLZTEM-2022”的均匀半空间实测数据结合，在已知均匀半空间条件下反演得到接收线圈的等效电路的rLC参数，即内阻r、电感L、分布电容C，得到的rLC参数可以用于未知地下介质浅层探测中过渡过程的矫正，且该方案易在接收机的FPGA(Field Programmable Gate Array)上实现，实验结果验证了基于Simulink对瞬变电磁接收机的过渡过程建模的正确性，以及对浅层探测中过渡过程的矫正的必要性，并且提供了一种高精度的瞬变电磁法浅层探测的方案。

2 方法简介

由于瞬变电磁每个接收线圈的分布参数都不一样，且分布电容C的计算非常困难且复杂，在实际中，也没有办法直接测量线圈的分布电容，因此本文提出了一种全新计算rLC参数的方案，即在正演的过程中考虑过渡过程的影响，通过基于Simulink对接收机过渡过程的二阶电路的建模分析，把接收线圈的rLC参数也加入到传统的正演模型中。当瞬变电磁系统的发射线圈和接收线圈大小和匝数设计好之后，通过传统的正演模型和Simulink对接收机过渡过程的二阶电路的建模，结合已知均匀半空间条件下的瞬变电磁系统“WLZTEM-2022”的实测数据，通过蒙特卡洛反演得到二阶电路的rLC参数(图1)。所以本文的正演过程分为两个部分：一个是基于传统瞬变电磁法的非零关断的电磁响应；另一个是基于Simulink对过渡过程二阶电路的建模。

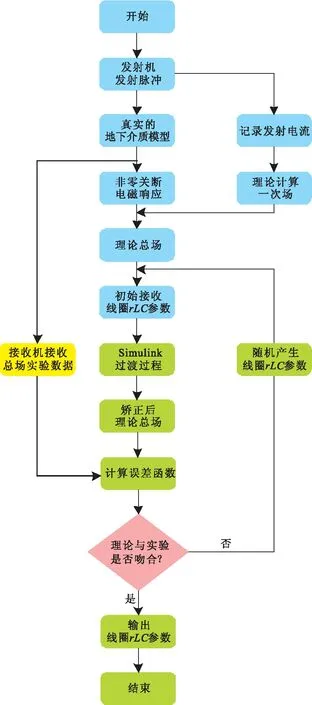
图1 基于Simulink对瞬变电磁系统的过渡过程的rLC参数反演流程Fig.1 rLC parameter inversion flow of transient electromagnetic system transition process based on Simulink

2.1 非零关断电磁响应

针对浅层的瞬变电磁系统中发射机的关断时间不可能严格等于零的问题，本文的解决方案是在瞬变电磁系统“WLZTEM-2022”的发射机中记录发射电流I(t)的数据，推导一次场的表达式，同时在传统的瞬变电磁响应的结果上做修正得到非零关断电磁响应的二次场信号。本课题组研制的瞬变电磁系统“WLZTEM-2022”的发射机发射电流的函数形式是e指数下降的I(t)=I0eα t。其中，I0为发射电流关断时的大小(单位：A)；α为衰减因子，决定关断的时间，可以由设计的电路来调节。

非零关断下一次场的电磁响应Hp(单位：A/m)可以由Biotsafar定理得到：

(1)

式(1)中,d代表当前积分元与单位向量dl之间的距离(m);θ是当前积分元与单位向量dl之间的夹角(°);β为当前积分元与接收线圈平面的夹角(°)。当计算的感应电压在中心回线的时候，参数满足θ=π/2，β=0且d=a，a为接收线圈的半径(m)，此时的一次场的大小为：Hp=I(t)/2a。在实际的应用中需要记录发射机的发射电流，以便理论计算一次场。

由于在实际应用中，瞬变电磁系统中并不是直接测量磁场强度的，而是根据法拉第电磁定理，通过构建磁环测量磁通量的变化，进一步测量得到感应电压，因此计算得到一次场的感应电压Up(单位：V)为：

(2)

其中S为接收线圈的面积(m2);μ0为真空中的磁导率(H/m)。

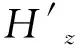
(3)

其中，Hz(t-s)对应理想关断电磁响应。对地下一维N层模型的理想关断电磁响应的理论计算已经十分成熟。对于理想关断响应的计算，通常采用先计算频域的响应，再通过傅里叶反变换转换到时域的方法。对于半径为a的发射线圈所激发的二次场，其对应地表的中心回线处垂直磁场可以表达为：

(4)

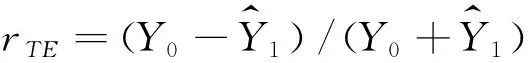
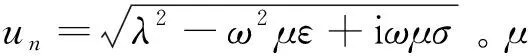
公式(9)中的Kj是Gaver-Stehfest变换的系数，wn对应Hankel变换的系数，h0和s分别对应Hankel变换中对λ采样的起始点和采样间隔。最后结合杜哈梅尔积分(3)得到非零关断下二次场的电磁响应：

(11)

(12)

其中,S对应接收线圈的面积(m2)。实际中，接收机接收到的信号是一次场和二次场感应电压叠加的总场的信号：

U0(t)=Up(t)+Us(t)

(13)

下面一节会继续讨论接收机接收到的总场信号U0(t)经过过渡过程之后的变化。

2.2 基于Simulink过渡过程的二阶电路建模

由于瞬变电磁仪的接收线圈中存在电感和分布电容，因此接收线圈在采集瞬变电磁响应信号时会存在充电和放电的过程，从而导致采集到的瞬变电磁响应信号与实际的瞬变电磁响应信号存在一定的偏差，如图2所示，该现象被称之为过渡过程。

图2 过渡过程示意图Fig.2 Diagram of transition process

瞬变电磁系统的接收机需要使用接收线圈观测瞬变电磁感应的电压，线圈和前置电路中的电容、电阻、电感构成二阶电路，如图3(a)所示是简化的接收线圈的等效电路: 其中R是阻尼电阻(Ω)，r是接收线圈的内阻(Ω)，L为接收线圈的电感(H)，C为接收线圈的电容(F,包含了分布电容)，U0(t)是接收线圈的感应电动势(V)，U(t)是信号经过过渡过程之后的输出电压(V)。

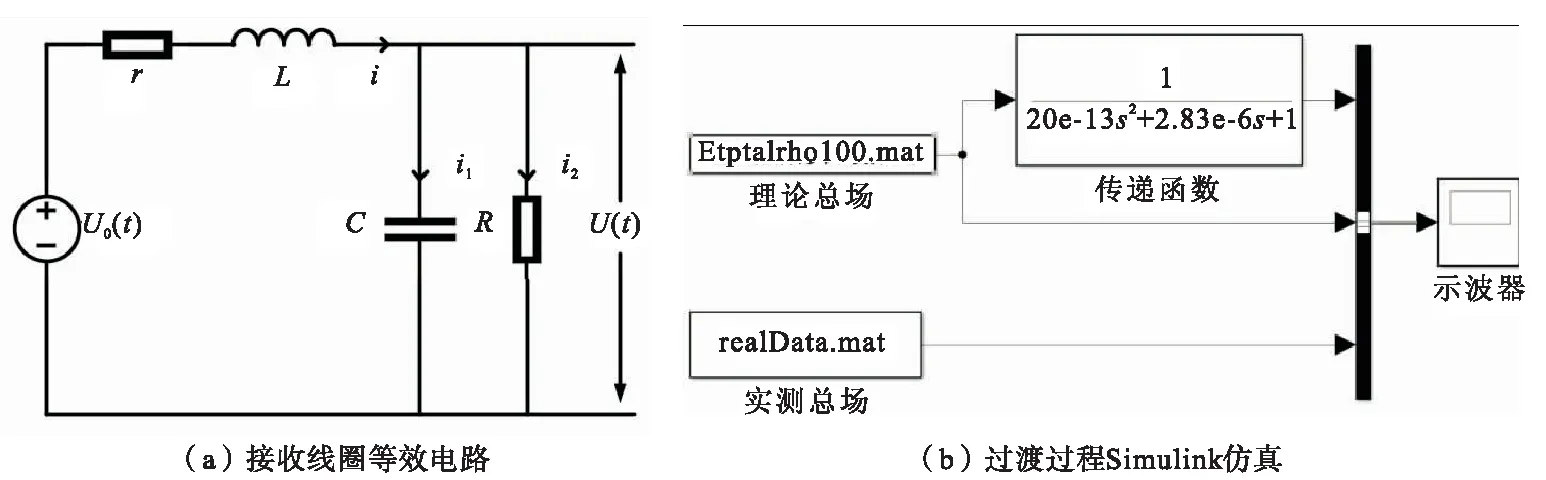
图3 简化的接收线圈等效二阶电路和Simulink仿真Fig.3 Simplified receiver coil equivalent second order circuit and Simulink simulation

根据基尔霍夫定理可得：

将式(15)带入式(14)可得到微分方程：

(16)

式(16)可简化为：

(17)

其中,ωb=ω0(1+r/R)1/2是电路的谐振频率;ω0=(LC)-1/2是线圈的固有频率;ζ=(r/(2L)+1/(2RC))/ωb是阻尼系数;R为阻尼电阻(Ω)。当ζ=1时，接收线圈工作与临界阻尼状态；当ζ>1时，为过阻尼状态；当ζ<1时，为欠阻尼状态。由阻尼系数可推导得到阻尼电阻：

(18)

本文基于Simulink仿真软件求解二阶电路的频域方程，对式(14)做拉普拉斯变化后得到频域的传递函数(图3b)：

(19)

式(19)表明过渡过程依赖于线圈的电阻r，电感L和电容C。由于电容的测量和计算非常困难，其中分布电容的值与线圈的大小、匝数、形状、材质等有关，传统的方法可以用谐振法[19]测量得到C参数的值，但是这种方法通常需要改变电路结构用于观察信号的波形，不利于电磁系统后期的调试和维护。本文提出一种新的测量方法，即用实测数据反演得到过渡过程对应的特性参数。

2.3 接收线圈分布参数的蒙特卡洛反演

传统的瞬变电磁的数据反演中，反演模型对应的是地下地质体结构的信息，由于未知参数较多，需要用到复杂的非线性反演的方法[20]。对于接收线圈分布参数的反演虽然也属于非线性反演，但由于其反演的参数较少，所以可以用简单的蒙特卡洛方法反演。对线圈的电阻r，电感L和电容C参数反演的步骤可以分为：

1)在特定的实验条件下，设发射线圈的半径a，接收线圈的面积S，地下均匀半空间的电导率ρ(Ω·m)，理论正演计算得到非零关断电磁响应下的总场的感应电压U0T(ti), 同时记录瞬变电磁系统“WLZTEM-2022”实测的发射电流I(t)和接收的总场的感应电压MT(ti)，其中i=1,2,3 …,N代表测量的第i个数据点。

2)设定接收线圈分布参数的初始模型M=(r,L,C)。

3)基于Simulink过渡过程的二阶电路建模得到矫正后的感应电压UT(ti)。

5)如果误差函数满足收敛条件ψ<ε，则反演过程结束；否则产生新的模型M=(r,L,C)+(Rand×r,Rand×L,Rand×C)返回步骤3)的计算。其中Rand表示随机数。

3 工程实例

3.1 瞬变电磁系统“WLZTEM-2022”

实验室自制的瞬变电磁系统“WLZTEM-2022”(图4)包含发射机和接收机部分，瞬变电磁仪的探测深度与精度不仅取决于发射机的性能，也取决于接收机的数据采集能力。发射机的发射电流越大，最大探测深度越深，信噪比也越大，发射机的关断时间越短，最小探测深度越浅；接收机的同步叠加次数越多、ADC(Analog-to-Digital Concerter)分辨率越高、放大器设计的越合理，也会使得信噪比越大，探测精度越高。

图4 瞬变电磁系统“WLZTEM-2022”实物Fig.4 The real “WLZTEM-2022” transient electromagnetic system

发射机和接收机之间通过“同步”接口实现时间上的同步，通过同步单元将同步信号发送给接收机用于确定开始采样的时刻。发射机中的电阻为可调电阻，用于改善发射电流波形，电流为可旋调节电流，逆时针旋转电流变小，发射接口与发射线圈相连，接收机的通道与接收线圈相连，USB接口用于插入U盘存储数据。该系统的操作流程如下：

1)打开开关；

2)设置发射机和接收机的参数，波形、频率、占空比等；

3)设置发射电流，根据电流波形来调节匹配电阻旋钮；

4)接收机采集数据并存储；

5)后期的数据处理和反演。

3.2 实验条件

利用上述实验室自制的瞬变电磁系统“WLZTEM-2022”，于2021年8月31日在校内进行了浅层探测实验，野外实验的地点为中国地质大学(武汉)西区数学物理学院后小树林，该实验采用中心回线装置，发射线圈为5 m×5 m，接收线圈的面积为9 m2, 发射电流I0=6 A，采样频率为2.5 MHz，叠加次数为1 024次。小树林的土壤在实验当天处于较湿状态，根据查阅的资料，较湿状态下的土壤电阻率大约为100 Ω·m。

3.3 数据采集

在上述野外实验的条件下，实时记录了瞬变电磁系统“WLZTEM-2022”的发射电流I(t)如图5(a)所示。图中显示的是发射电流的对数logI(t)关于时间的t的实测数据。根据最小二乘法线性拟合得到发射电流的函数为：I(t)=6e-182 240t,瞬变电磁系统“WLZTEM-2022”的接收的实测数据MT(ti)如图5(b)所示，数据的时间间隔为0.4 μs,由接收机的采样率(2.5 MHz)确定。

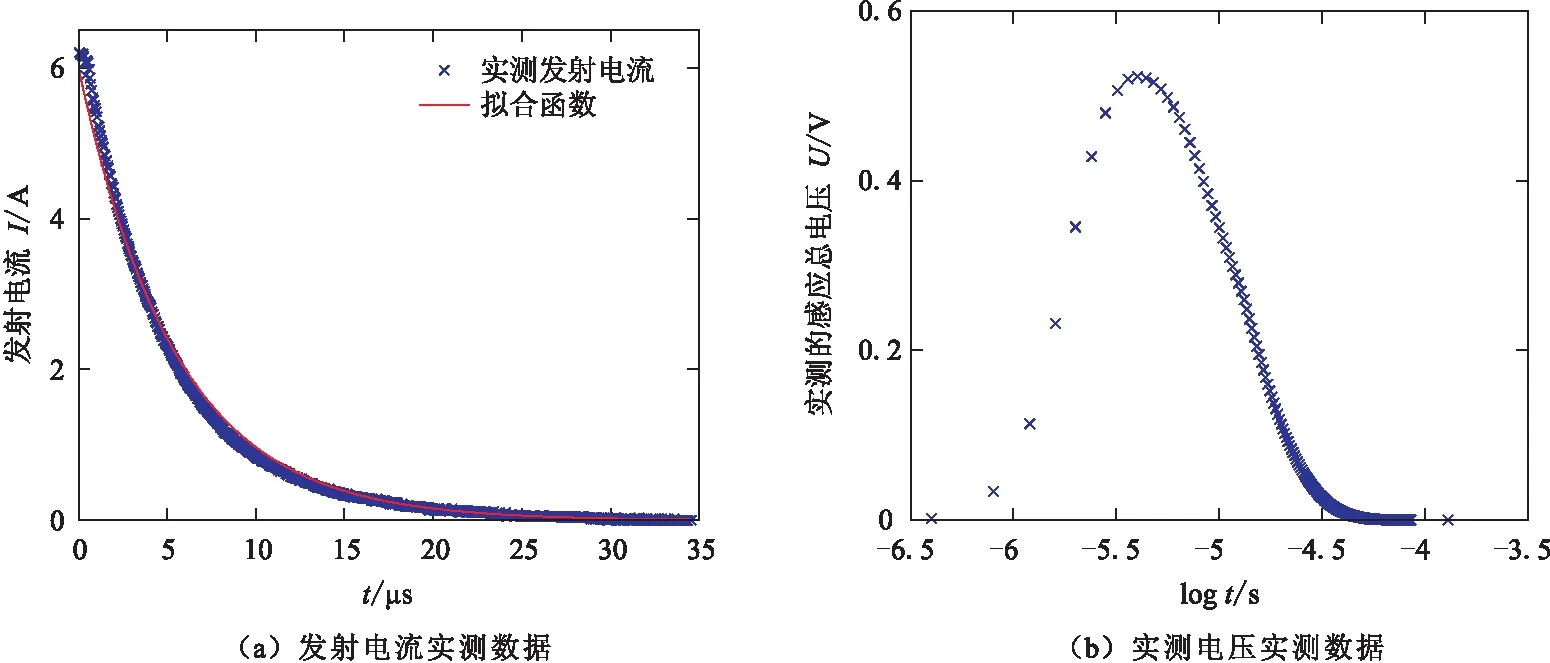
图5 瞬变电磁系统“WLZTEM-2022”野外实测数据Fig.5 Field measurement data of transient electromagnetic system “WLZTEM-2022”

3.4 rLC参数反演

在对过渡过程的rLC参数反演之前，需要理论计算的非零关断电磁响应U0(t)，如图6所示。图6(a)是根据发射机发射的实际电流理论计算的一次场感应电动势Up(t)，图6(b)是根据野外实际的均匀半空间的电阻率ρ所对应的非零关断条件下的二次场感应电动势Us(t)。

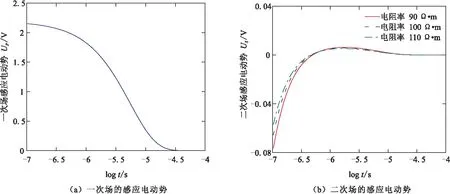
图6 理论计算的非零关断电磁响应(未经过过渡过程)Fig.6 Theoretically calculated non-zero turn off electromagnetic reponse (without transition process)

本文考虑到了均匀半空间的电阻率ρ测量的不准确性，在模型中计算了与理想值偏差±10 Ω·m 的结果。从图6(b)中可以看出，均匀半空间的电阻率ρ的变化对二次场的影响很小。最后根据理论正演计算得到非零关断电磁响应下的总场的感应电压U0(t)=Up(t)+Us(t)，挑选不同时段的理论数据U0T(ti)与接收机实测的数据MT(ti)反演过渡过程的rLC参数。

根据2.3节接收线圈分布参数的蒙特卡洛反演方法，得到不同的均匀半空间的电阻率ρ和数据点数N条件下的反演结果，如表1和图7所示。表1中的误差ψ0和误差ψ分别表示未经过过渡过程矫正前和经过过渡过程矫正后的误差函数。 从表中可以得知,矫正后的误差ψ比误差ψ0更小，矫正后的误差定量上比矫正前的误差约减小了3倍。 图7(a)是未矫正的总场与实测数据的对比，从结果中可以看出,未经过过渡过程处理的总场与实测数据在早期存在较大的差异，而且总场关于时间变化的函数在定性上就有很大的区别：未矫正的理论正演的曲线U0T(ti)关于时间是单调降低的；但是瞬变电磁系统“WLZTEM-2022”实测接收到的总场的感应电压MT(ti)在早期有一个上升的过程。图7(b)是利用实测数据的前20个数据点反演的结果，反演得到的曲线与实测的数据在早期(t<5 μs)和晚期(27 μs 17 μs)都能够吻合，得到的接收线圈的rLC参数为：r=[1.420 Ω,1.508 Ω]，L=[2.457e-6 H,2.851e-6 H]，C=[1.215e-8 F, 1.711e-8 F]。

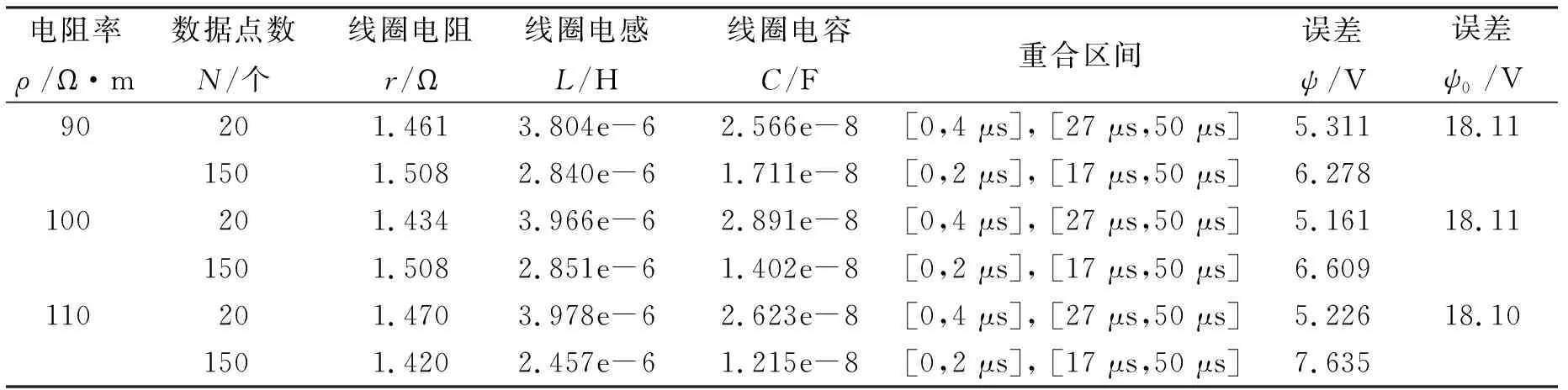
表1 不同的均匀半空间的电阻率ρ和数据点数N条件下的反演结果

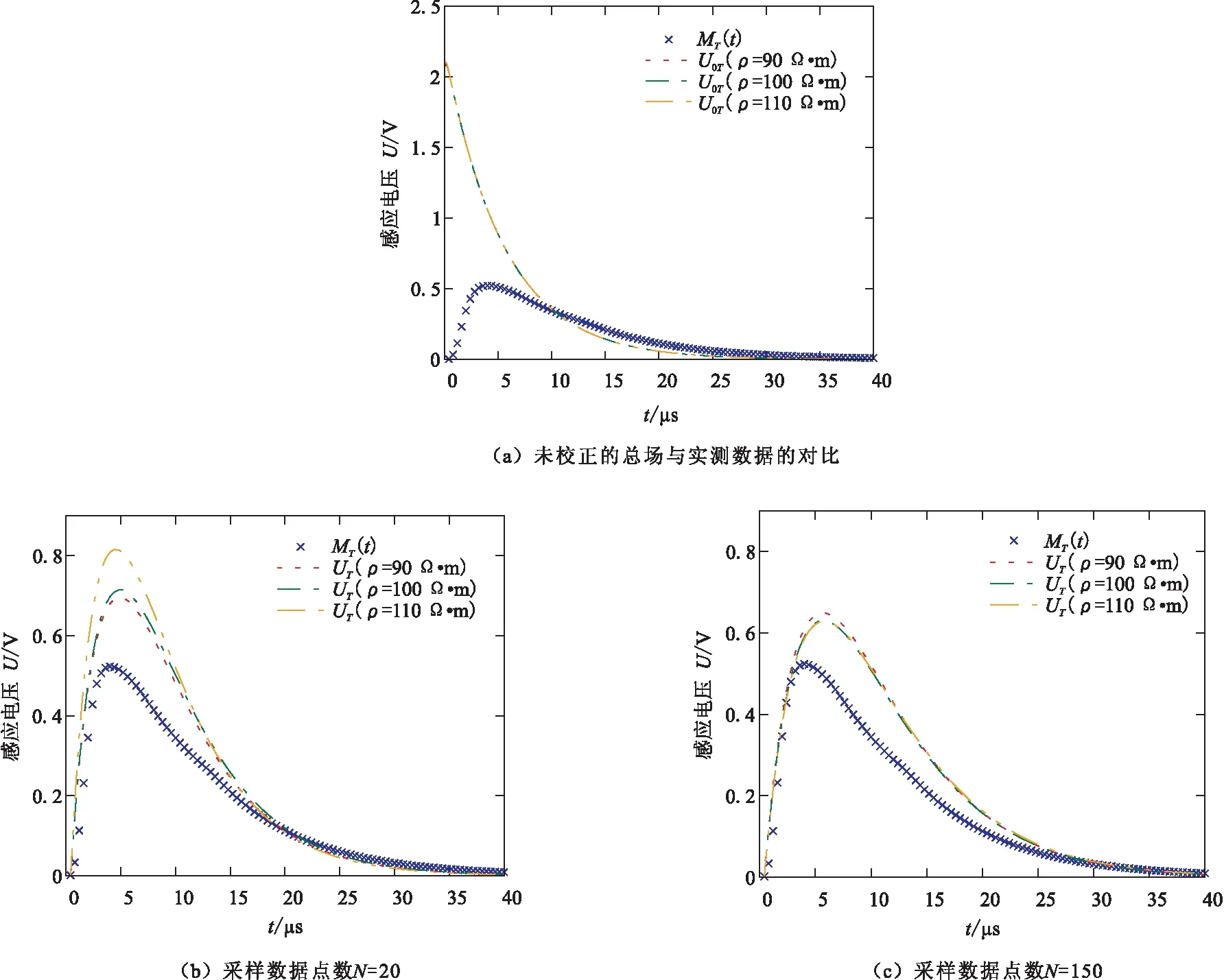
图7 过渡过程矫正前后的总场与实测数据的对比Fig.7 Comparison between the corrected total field by the transition process and measured data

对比不同数据长度N的反演结果可以发现数据长度N对电阻r的影响较小，数据长度N对电感和电容的值影响较大。对于浅层的探测应该用早期的数据反演，从而得保证早期的信号与实测数据更吻合；对于传统的深部探测应该用晚期的数据反演，从而得保证晚期的信号与实测数据更吻合。此外数据长度N越大，反演得到的电感和电容就越小，根据电路理论分析，电容和电感越小，对应二阶电路的时间常数越小，信号变化越剧烈，这个结论也可以从反演的曲线得到，从而从理论自洽的方面验证反演和过渡过程建模的正确性。

3.5 过渡过程矫正对浅层探测精度的研究

3.2节通过对接收线圈二阶电路的建模得到了确定测量环境下rLC的实验值，接下来用反演得到的rLC的值计算不同的地下层状地质模型的总场的响应，从而研究过渡过程对TEM浅层探测精度的影响。具体地，地下层状地质模型采用三层模型。第一层参数分别为h1=1 m,2 m,3 m,4 m,ρ1=1 000 Ω·m；第二层参数为h2=1 m,ρ2=1 Ω·m；第三层参数为ρ3=1 000 Ω·m。其模型的参数设置对应于探测浅层埋藏的非电导体和电导体的差异。其中过渡过程的rLC参数取值取自上一节的蒙特卡洛反演得到的一组参数值：r=1.434 Ω，L=3.966e-6 H，C=2.891e-8 F。

图8是过渡过程矫正前后的总场随地下地质模型(第一层探测深度h1)的变化。图8(a)感应电压U0T(t)和UT(t)的对数图，可以看出过渡过程矫正前后早期信号有较大差异，并且差异随着时间的增加而减小。以理论曲线U0T(h1=4 m)和UT(h1=4 m)为例，两条曲线在时间t>70 μs之后重合；同时从数值模拟的结果来看，过渡过程可以矫正早期70 μs内的数据。这里值得注意的是，过渡过程对信号的矫正对整个测量时间内的信号都会矫正，只是晚期的信号受过渡过程的影响较小。

图8 过渡过程矫正前后的总场对浅层探测的影响Fig.8 The influence of the total field before and after the transition correction on shallow detection

另一方面从图8(b)中得到过渡过程矫正前后浅层探测的灵敏度的变化。通常对于浅层探测的瞬变电磁法系统的接收机的测量时间的要求为小于1 μs。当接收机能够真实记录早期信号(t<1 μs)的时候，测试的仪器才能够满足探测埋藏在浅层(0～5 m)的非电导体和电导体之间的差异。值得注意的是，在实际的测量中仪器测量得到的曲线是经过过渡过程(rLC电路)影响之后的UT(t)曲线，其测量的结果(t<1 μs)对地质模型(h1)的变化不敏感，此时的灵敏度几乎为零，存在浅层探测(0～5 m)的测量盲区。然而如果对其数据通过反向的过渡过程的矫正，可以得到理论的总场的数据U0T(t)的曲线，可以看到曲线U0T(h1=1 m)， 曲线U0T(h1=2 m)，曲线U0T(h1=3 m)和曲线U0T(h1=4 m)在早期μs有明显的差异，此时可以得到有效的可测量的灵敏度。综上所述，理论上通过对测量数据的反向过渡过程的矫正可以提高瞬变电磁系统“WLZTEM-2022”的浅层(0～5 m)的探测能力。

4 结 论

1)通过理论数据与瞬变电磁测量的实验数据对比，发现未经过过渡过程处理的总场与实验数据在早期有较大差异，验证了对浅层探测中过渡过程的矫正的必要性。

2)通过对瞬变电磁仪器接收机的过渡过程建模及对接收线圈分布参数的蒙特卡洛反演，可以得到线圈的rLC参数，经过过渡过程后的理论曲线与实测的曲线在早期吻合，通过计算本文定义的误差函数ψ，经过过渡过程校正后的误差定量上比矫正前的误差约减小了3倍。

3)反演的结果表明反演的数据长度会影响反演的rLC参数，反演的数据长度越大，反演得到的rLC参数越小，得到的感应电压曲线变化越剧烈；本文提出的反演算法可以直接移植到接收机的FPGA上。

4)把反演得到的过渡过程中rLC参数加入到传统的TEM正演的算法中，可以得到对过渡过程准确建模后的早期(t<1 μs)的理论总场曲线，从而提高瞬变电磁系统浅层(0～5 m)的探测能力。