隧道空间对高密度电法在掌子面及侧壁富水构造探测中的影响研究
张付军,胡 俊,胡正旺,蔡佳豪,赵元科
(1.甘肃长达路业有限责任公司,甘肃 兰州 730000;2.甘肃省交通科学研究院集团有限公司,甘肃 兰州 730000;3.甘肃省桥梁隧道健康监测与安全评估技术重点实验室,甘肃 兰州 730000;4.中国地质大学 地球物理与空间信息学院,湖北 武汉 430074;5.中国地质大学 地球内部多尺度成像湖北省重点实验室,湖北 武汉 430074)
1 引 言
我国是隧道建设数量最多、发展最快、地质环境及结构形式最复杂的国家[1]。突涌水是隧道修建过程中造成经济损失和人员伤亡最严重的地质灾害[2,3],隧道掌子面或侧壁的富水构造作为突涌水的灾害源[4,5],给隧道施工安全带来巨大危害,常造成重大的灾害和生命财产损失[6],快速探测富水构造是保障安全生产的关键。地球物理方法由于具有经济快速探测的优点,被广泛地应用于隧道的富水构造探测[7,8]。由于地质体电阻率对含水量变化极为敏感[9],以电阻率探测为目的的高密度电法具有富水结构探测的良好前提,研究人员针对其反演算法及压制多解性方面和工程应用开展了诸多的研究和尝试[10,11]。如刘斌等[12,13]将地震反射、探地雷达等方法获取的异常体空间结构和形态特征作为先验信息,采用结构约束方法反演成像;李术才等[14]提出在反演过程中施加不等式约束,将地质体电阻率变化范围的上下限信息的不等式约束施加到反演方程;王传武等[15]提出将多种地球物理探测手段获得的已知信息构建的参考模型作为约束施加到电阻率反演方程中。上述方法均有效减少了反演结果中的假异常和多余构造。
在地表起伏不显著的条件下,通常采用半空间条件下的装置系数计算视电阻率。但与地表高密度电法的正反演计算不同,隧道是对全空间模型进行了局部开挖,半空间假设显然难以适用。因此在隧道三维模型中,无法用解析公式计算视电阻率,而全三维的正反演算法通常计算量大,而且常用的商业软件难以对隧道三维模型进行快速建模和反演。已有研究表明,即使在地表地形变化较显著时,半空间视电阻率计算方法也会带来较明显的误差[16,17]。但在隧道高密度电法应用中,已有研究人员认识到了采用半空间假设的公式在隧道数据采集时的视电阻率误差,并针对一维电阻率测深和反演解释方面进行了探索研究[18,19]。随着仪器的进步和计算能力的提升,二维、三维正反演方法已经广为应用,在异常体三维形态和分布特征方面的探测更有优势。但应用高密度电法二维超前探测时,视电阻率计算误差还缺乏定量研究,并且对用该方法得到的视电阻率数据进行反演的结果是否会存在显著的误差也还缺乏清楚的认识。
本研究拟建立隧道三维正演模型,采用数值方法计算隧道非半空间的装置系数,并与半空间计算公式得到的装置系数进行对比,分析在隧道不同部位进行数据采集时二维假设带来误差的特征,以及有误差视电阻率反演计算结果的偏差程度。
2 数值模型及正反演计算
2.1 视电阻率计算
正反演计算以偶极—偶极装置为例,在地表为平坦半空间条件下该装置的装置系数k的计算公式为[20]:
k=πan(n+1)(n+2)
(1)
视电阻率ρ(Ω·m)计算公式为:
(2)
其中,ΔU为电势差,V;I为电流,A。
在隧道三维模型中,先将模型的电阻率设置为1 Ω·m,由模型数值计算方法得到相应位置的电势差与电流的比值(ΔU/I),而隧道掌子面或侧壁计算的理论视电阻率值应为1 Ω·m。因此可以得到数值方法计算的非半空间条件下的装置系数为:
(3)
为评估非半空间地形装置系数与半空间装置系数之间的相关关系,计算装置系数比值定义为地形因子:
(4)
当地形因子t=1时,表明地形对视电阻率不产生影响;当t>1时,表明地形使视电阻率增加;而t<1时,表明地形使视电阻率值降低[17]。
2.2 正反演计算方法
正反演计算采用了高密度电法开源软件BERT[21],该软件能进行结构和非结构网格离散,采用有限元计算方法,在处理不规则地形时具有很好的适应性,并能进行二维、三维正反演,主要反演算法目标函数为:
(5)
其中,D=diag(1/εi)为观测数据的误差权重;d为观测数据;f(m)为模型正演计算结果;λ为正则化参数;C为常数矩阵,用以描述模型先验特征;m0为先验模型。
为研究隧道三维结构引起的视电阻率偏差对反演结果的影响,分别对半空间假设计算的视电阻率值和考虑隧道三维结构视电阻率值进行了反演。反演时将正演模拟得到的考虑三维地形的装置系数作为已知数据带入反演,反演迭代过程中首先计算均匀半空间条件下观测点处的电势和电流值;然后将考虑全三维地形时得到的装置系数用于计算视电阻率值,从而在反演过程中将三维地形影响消除;最后对比反演结果与正演模型,以评估不同视电阻率计算方法对反演结果的影响。
3 隧道掌子面富水结构探测模型
为研究隧道掌子面高密度电法探测时隧道空间对视电阻率的影响,建立正演模型如图1所示,模型几何尺寸为200 m×200 m×200 m,隧道直径12 m,掘进长度50 m(图1a)。在隧道掌子面处共布设60个电极,电极间距0.2 m,测线布置沿隧道直径、呈水平方向。正演模拟计算采用偶极—偶极装置,其中电极间隔系数n取值1~6,偶极长度a为1~19倍电极距。计算的视电阻率值叠加了5 %的随机噪声。正演模型采用四面体网格进行离散,为提高数值计算精度,模型网格化时在电极附近位置进行了加密(图1b)。
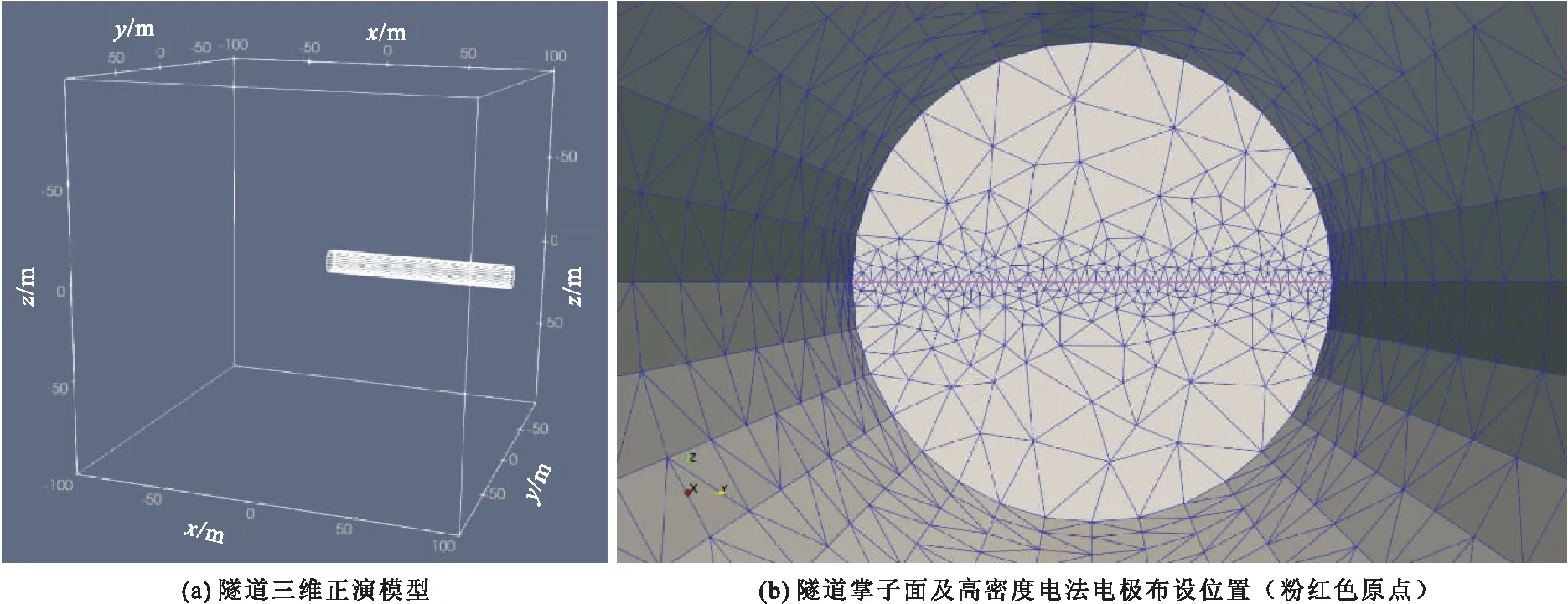
图1 隧道掌子面高密度电法正演模型Fig.1 High density electrical forward modeling of tunnel face
隧道三维模型掌子面探测时的地形因子如图2所示,可以看出,半空间假设计算的视电阻率值与真实值存在较为显著的差异。总体而言,隧道掌子面处的三维地形使得地形因子小于或等于1。而且地形效应的影响在靠近掌子面的边缘和较深处最为明显,采用半空间假设计算的视电阻率值误差最大能达到52 %。
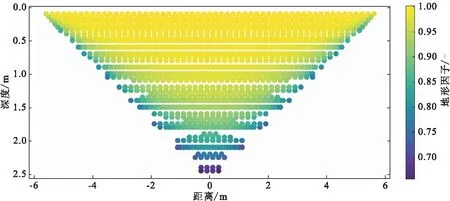
图2 隧道三维模型掌子面探测地形因子Fig.2 Terrain factor of 3D model in tunnel face detection
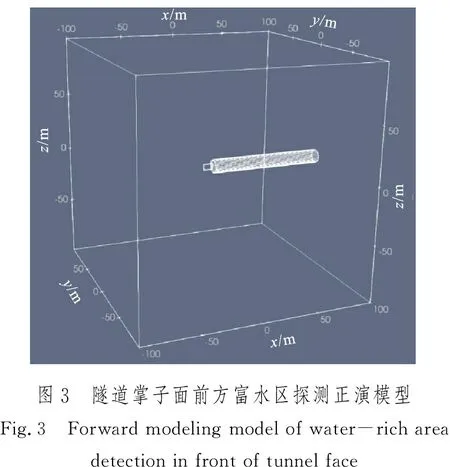
基于上述模拟得到的隧道三维模型掌子面处的装置系数,可以对相同几何结构模型,但以掌子面前方富水区为探测目的的模型进行模拟。模型结构与图1中的均匀空间相比,在掌子面前方增加了几何尺寸为8 m×2 m×5 m的长方体形富水区,电阻率值为10 Ω· m,距离掌子面距离为1.0 m,其余背景区域电阻率值为100 Ω·m(图3)。测线布置与图1(b)中相同,在隧道掌子面处共布设60个电极,电极间距0.2 m,测线布置沿隧道直径、呈水平方向。正演模拟计算采用偶极—偶极装置。
在图3的掌子面富水结构探测模型中,在半空间假设条件下和隧道三维模型计算的视电阻率值如图4所示。可以看出,半空间假设得到的视电阻率值比真实值偏高,视电阻率值范围为46.2~144 Ω· m,而三维模型数值计算得到的视电阻率值为44.6~122 Ω· m。但总体而言,半空间假设得到的视电阻率数据空间分布特征与真实视电阻率值大致相同。
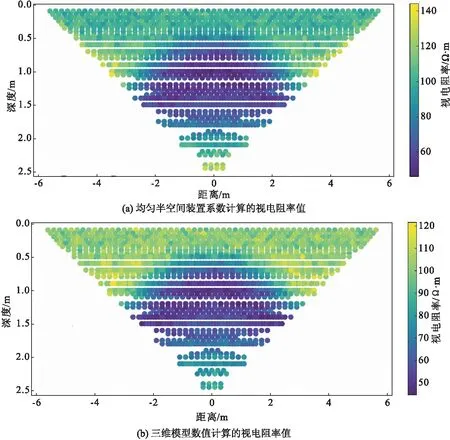
图4 隧道掌子面探测时三维模型对视电阻率值的影响Fig.4 Effect of 3D model on apparent resistivity in tunnel face
将上述两组视电阻率值进行反演,得到反演电阻率模型如图5所示。两组反演结果均较好地反应出了富水区域的空间位置和距掌子面的距离,且富水区域反演电阻率值与真实值较为接近。但由于掌子面测线长度限制,探测深度小于3 m,无法识别出富水区域的底界面。因此,虽然半空间假设视电阻率值存在一定误差,但反演结果却与真实视电阻率值的反演结果具有较好的一致性。其原因主要在于,在隧道掌子面进行高密度电法探测时, 半空间假设计算视电阻率值的误差主要在掌子面边缘和较深处,偶极—偶极装置在测线两段的数据覆盖度较低,而且高密度电法分辨率随深度增加而迅速降低,也即在这两个区域观测数据对反演结果的约束较差,反演结果更多地受到初始反演模型的约束[22],因此虽然这两个区域的视电阻率数据存在一定误差,但反演结果差异较小。
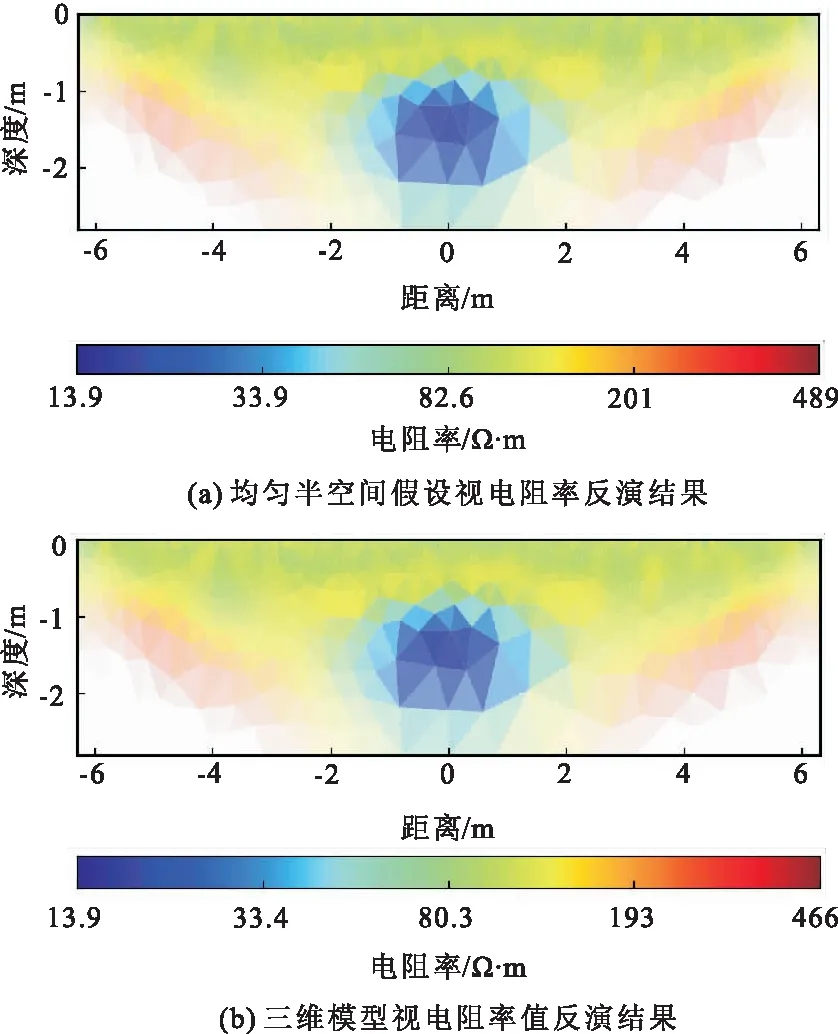
图5 掌子面探测不同视电阻率数据反演结果Fig.5 Inversion results of different apparent resistivity data in palm-surface detection
4 隧道侧壁富水结构探测模型
隧道侧壁富水结构模型如图6(a)所示,隧道三维模型几何尺寸为200 m×200 m×200 m,隧道直径12 m,掘进长度50 m。模型中的富水区域几何尺寸为8 m×5 m×5 m,富水区距侧壁距离1.5 m。富水区电阻率设置为10 Ω· m,其余背景区域电阻率值为100 Ω· m。高密度电法测线沿隧道侧壁布设,距隧道底部高6 m,采用偶极—偶极装置,共布设电极60个,电极距0.8 m,测线总长度49.8 m(图6b)。
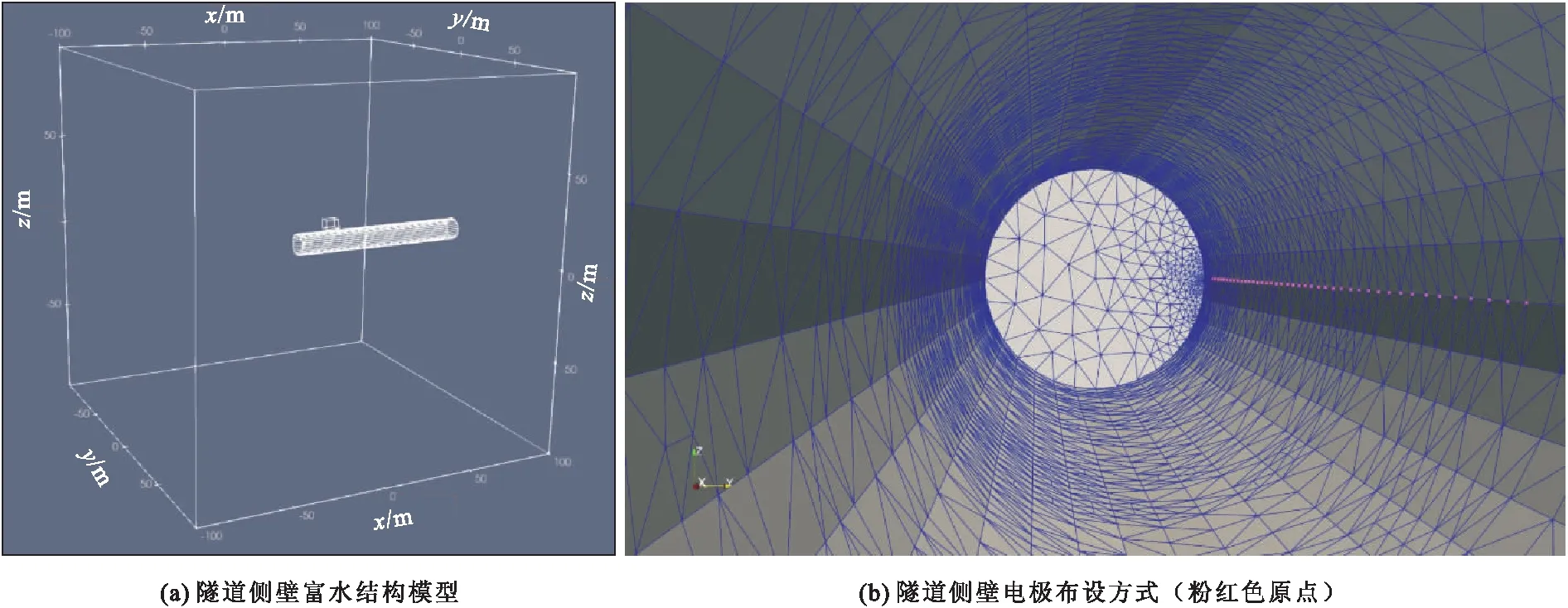
图6 隧道侧壁富水结构探测模型Fig.6 Water-rich structure detection model of tunnel sidewall
隧道三维模型侧壁高密度电法探测几何效应对视电阻率值的影响如图7所示。由图7可知,在隧道侧壁靠近掌子面一端,三维地形使得视电阻率值降低最为明显,在间隔系数较小的浅层区域,视电阻率值也略有降低。但隧道地形使得在较大的深度处的视电阻率显著增加,最大视电阻率值达到半空间假设计算值的约1.6倍。其原因在于,越远离隧道,隧道空间的影响越弱,更接近于全空间假设,而在全空间条件下装置系数是半空间的2倍。
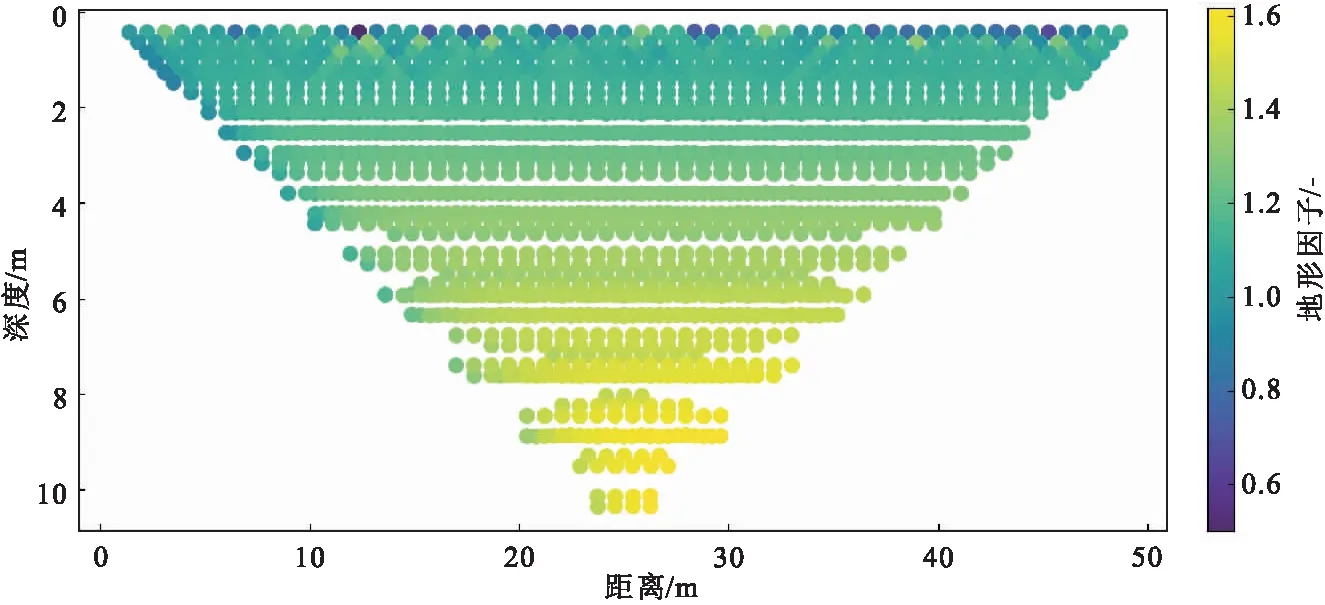
图7 隧道三维模型侧壁探测地形因子Fig.7 Terrain factors of 3D mode in tunnel sidewall detection
与掌子面处的视电阻率特征类似,半空间假设计算的视电阻率值和三维模型数值计算得到的视电阻率值的空间分布特征类似,数值最大差异出现在侧壁与掌子面界面和较大深度处(图8)。
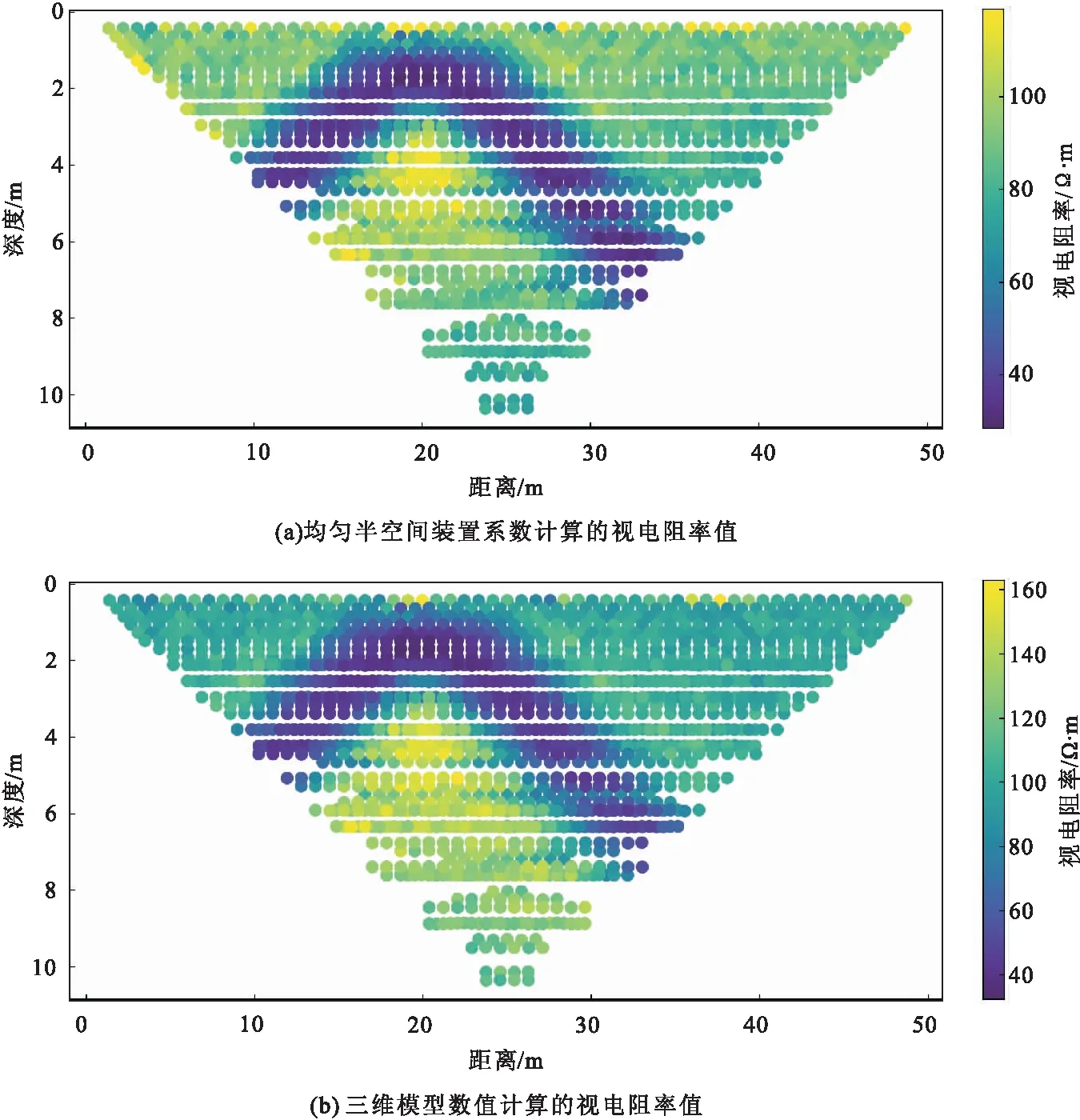
图8 隧道侧壁探测时三维模型对视电阻率值的影响Fig.8 Effect of 3D model on apparent resistivity in tunnel sidewall detection
两组视电阻率的反演结果呈现类似特征(图9),均能较好地识别富水低阻区的空间位置和几何形状,且最小电阻率9 Ω· m与正演模型的富水区电阻率值差异很小,反演结果具有较好的精度。但两组数据的反应结果中,在低阻富水区域下部均呈现了高阻区,其电阻率值大于200 Ω·m,与实际的正演模型偏差较大。其原因在于,在地表供电时,电流更倾向于沿低阻路径传播,对低阻区以下部位起到了屏蔽作用,因此对该区域的分辨率降低,观测数据无法对反演模型起到较好的约束作用,反演结果误差较大。
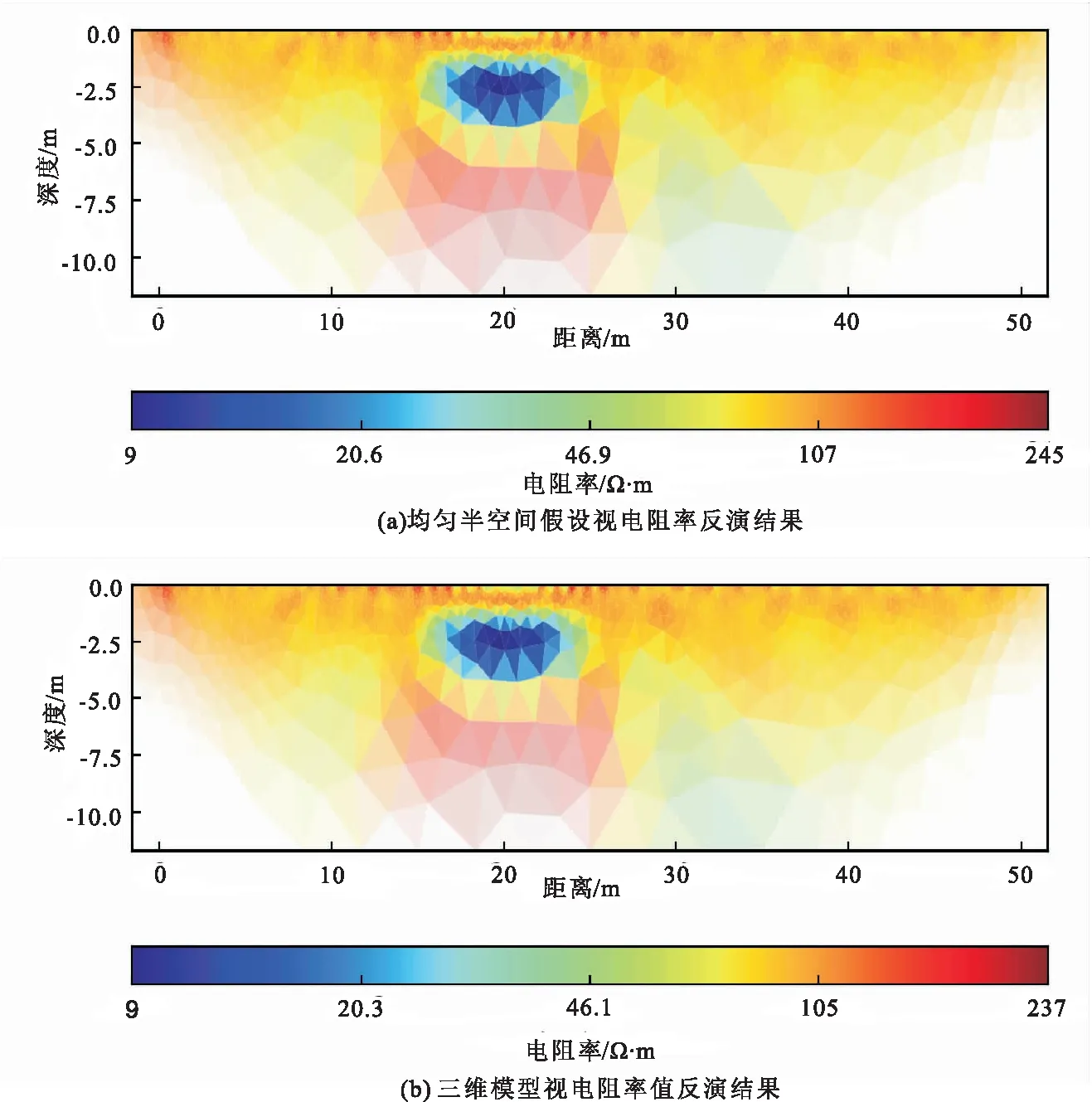
图9 隧道侧壁探测不同视电阻率数据反演结果Fig.9 Inversion results of different apparent resistivity data in tunnel sidewall detection
5 结 论
1)采用高密度电法在隧道掌子面处布设电极时,若忽略隧道三维结构的影响,采用半空间条件下的视电阻率计算公式,会使视电阻率计算值低于真实值。误差最显著的区域在靠近掌子面的边缘和较深处,采用半空间假设计算的视电阻率值误差最大能达到52 %。但视电阻率总体特征与真实值基本保持一致。
2)采用半空间视电阻率计算公式得到的视电阻率值与真实视电阻率值的反演结果基本保持一致。说明在掌子面处探测时,不考虑隧道三维地形对反演结果的影响,采用二维反演算法进行正反演计算的误差较小。但由于掌子面测线长度限制,探测深度较浅。
3)若在隧道侧壁进行探测,半空间假设带来的视电阻率计算误差比在掌子面处更为显著。在靠近掌子面的侧壁处视电阻率增加,而在较大深度处视电阻率值降低。误差范围在0.9~1.6倍之间。
4)在隧道侧壁探测时,采用两种方法计算的视电阻率值反演结果基本一致,说明在隧道内部应用二维反演算法带来的误差可以忽略。但在对富水低阻区进行探测时,低阻区对以下部位起到了屏蔽作用,因此对低阻区以下部位,观测数据无法对反演模型起到较好的约束,反演结果误差较大。

