基于非线性Gauss-Markov模型与广义EIV模型的矿区高程拟合方法研究

1 绪论

随着中国经济迅速发展,对矿业资源的需求量逐渐增大,因矿区开采所带来的地表沉陷严重破坏了矿区地表环境[1]。因此,对矿区地表进行变形监测具有重要的研究意义。而为了掌握煤矿开采过程中地表沉陷的规律,就必须对开采沉陷进行现场测量[2]。目前,地表沉降观测传统监测方法是采用水准测量的方式获取竖直方向的位移,而水准测量往往需要测量人员进行较为复杂的实地测量。面对待测点分布广、数量多的情况,测量的外业工作大大增加,尤其是在山区等复杂地形,外业工作也更加困难[3]。卫星定位技术可以快速获取点位的大地高,但其空间基准为参考椭球面,受高程异常的影响,导致GNSS获取的大地高难以直接利用[4]。

针对矿区高程异常拟合问题,常采用二次多项式作为拟合方程,并采用非线性Gauss-Markov模型求解二次多项式的参数[5-6]。面对拟合的病态问题,韦子豪等提出采用岭估计方法以解决二次曲面法实施高程拟合过程中的法方程病态问题,结果表明该方法有效地解决了法方程的病态问题且提高了高程拟合的精度[7]。李睿等用多项式阶数对高程异常拟合精度进行了分析,研究表明高程异常拟合精度与多项式阶数并无明显的联系[8]。

在高程异常拟合问题中,观测值包括点位的平面坐标和高程异常值,而线性Gauss-Markov模型仅顾及了高程异常含有的随机误差,尚未考虑平面坐标含有的随机误差。面对此问题,可以采用EIV(error-invariables, EIV)模型进行描述,对此模型的求解方法称为整体最小二乘(total least squares, TLS)[9]。楚彬等基于EIV模型使用比例整体最小二乘(scale TLS, STLS)得到估计参数,从而提高了高程异常拟合精度[10];赵辉等基于EIV模型研究加权总体法解决系数矩阵存在误差的问题,研究表明EIV模型通过加权法可以更好地提高高程异常拟合精度[11];袁豹等基于EIV模型对比分析了加权法、最小二乘法与加权总体法,通过计算结果,验证了加权总体法可以得到更准确的函数模型参数[12]。由于系数矩阵中除了非随机元素还存在固定元素,对系数矩阵直接定权会造成歧义,因此EIV模型的求解方法存在歧义。然而面对复杂的非线性问题,EIV模型则难以准确描述。针对上述两个问题,WANG等提出了广义EIV模型并将其应用于三维基准转换中。面对矿区开采沉陷高程异常拟合问题,二次多项式的非线性程度较高,因此更适合采用广义EIV模型进行描述[13]。

综上所述,论文针对矿区开采沉陷的高程异常拟合问题,以二次多项式作为拟合模型,分别采用非线性Gauss-Markov模型和广义EIV模型进行求解,并通过实测实验与仿真实验对两个模型的数据进行验证,对比分析两种模型的精度和效率,研究适用于矿区高程异常拟合方法。

2 高程异常拟合模型与求解方法

2.1 基于二次多项式的高程异常拟合模型

GPS测定的是大地高H大,而在各种比例测图中,更多的是使用正常高H正。正常高是由地球重力场定义的高程参考面。GPS大地高与正常高之间的关系如下式:

式中,ξ为高程异常,表示参考椭球面与似大地水准面之间的高程差。在用GPS测定正常高时,关键问题就在于高程异常的精确求定,目前主要有两种途径:(1)物理大地测量方法;(2)几何方法。

论文运用几何法中的曲面拟合中的二次曲面拟合模型,其模型如下式:

2.2 求解方法

2.2.1 基于非线性Gauss-Markov模型的求解方法

假定存在一个n×m阶系数矩阵A,X为m维未知参数向量,L为n维随机观测值向量,并且假设系数矩阵A为满秩,正定矩阵为权矩阵P,存在下列满秩的Gauss-Markov线性模型:

函数模型:

随机模型:

其中,L是n×1的观测向量,X是t×1的待估参数向量,A是n×t的系数矩阵,且满足Rank(A)=t＜n,e为n×1的随机误差向量,E(e)和D分别表示为e的数学期望和协方差阵,Q为协因数阵,P为权阵,σ0为单位权中误差。

所以误差方程为:

平差计算是对随机观测值L进行处理,为使平差后的参数估值具有较好的数学性质,则应约束平差的函数模型。最小二乘法的平差准则是:

利用自由极值原理,将式(6)对X求导并让其导数为零:

将所得上式转置又能得到:

将式(3)代入上式,能得到:

可求得待估参数的最小二乘解为:

验后单位权中误差为:

即估值的参数协方差矩阵由协方差传播定律计算如下:

2.2.2 广义EIV模型的求解方法

当观测向量和系数矩阵均为含有误差时的函数模型称为整体最小二乘模型,又称EIV(error-invariables)模型,具体函数模型为:

其中,f表示n×1维的抽象函数,L和a分别表示n×1和m×1维的观测向量,eL和ea分别表示对应的随机误差向量,X表示t×1维的待估参数向量。

广义EIV模型的随机模型为:

其中,Q是误差向量e的协因数阵,为单位权方差,Qaa表示误差向量ea的协因数阵,QLa和Qa L为eL和ea之间的互协因数阵。

广义EIV模型的估计准则为:

针对广义EIV模型,可以采用Lagrange乘数法来进行求解。假设待估参数X和误差向量ea的近似值分别为X0和e0a,对式(15)在近似值X0和e0a处进行展开:

其中,

根据式(15)和式(16)来构建Lagrange目标函数:

其中,J=InB[ ],K为Lagrange乘数向量。

由式(19)可得误差向量的表达式:

由上式(22)代入式(21)可得Lagrange乘子的表达式:

其中,l0=L-f(a-e0a,X0)+Be0a。

将上式(23)代入式(20),可求得参数改正数表达式:

根据上式(24),更新待估参数为:=X0+。

将式(23)代入式(22),并联立式(15),可得误差向量的表达式:

采用Lagrange乘数法进行求解时也需要进行迭代计算,具体步骤入下:

(1)给定参数初值X0和e0a;

(2)第i次迭代,计算(更新)设计矩阵A、B和l0;

(3)计算矩阵QJ=JQJT

根据计算的参数改正数更新参数:=X0i+d并且计算误差向量预测值:

其中,自由度r=n-t。

3 案例分析

根据2.2.1内容,基于非线性Gauss-Markov模型的高程异常拟合相关矩阵的形式如下:

首先,基于非线性Gauss-Markov模型,误差方程为:

计算中已知点的个数。

根据式(11)可得未知系数的平差值为:

而对于广义EIV模型,其观测方程为:

将上式采用Taylor级数进行线性化,可得:

对于上式整理可得广义EIV模型的误差方程:

式中,l=ξ-f(a0,e0)+Be0;G=[IB];e=[eζexey]T;ξ=(ξ1ξ2…ξn)T;

β=(da01da02da03da04da05da06)T;I为单位矩阵。

根据2.2.2中的迭代算法即可求出广义EIV模型的估计结果。

3.1 实测实验

图1展示为在某矿区煤炭开采的走向线与倾向线布设的沉陷观测点,共计94个。将数据中的80个点作为拟合点,分别采用非线性GM模型和广义EIV模型进行解算,将解算的多项式参数与14个检核点平面坐标计算检核点的高程异常值,并与实测结果相比较。多项式参数结果见表1。图2展示了检核点高程异常的差值序列,检核点高程异常插值序列的外符合精度见表2。由于缺少观测值的方差协方差信息,在两种方案的随机模型为单位阵,即解算过程中采用的等权方式。

根据表1、表2和图1可以看出:非线性GM模型与广义EIV模型的参数与检核点外推结果一致且精度相当,其中检核点的外符合精度在10-8处才产生差异,但非线性GM模型的计算效率要优于广义EIV模

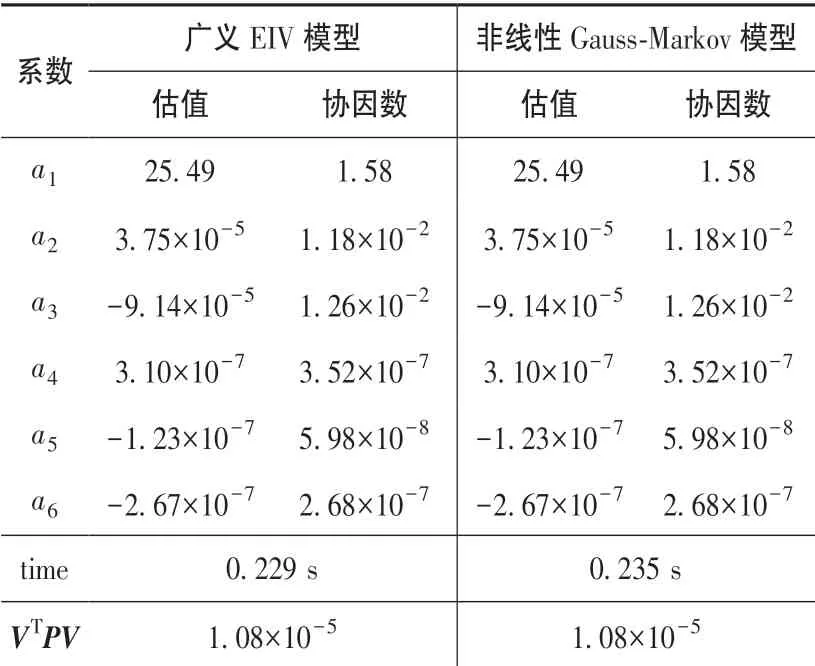
表1 多项式系数拟合结果Table 1 Results of the polynomial coefficient fit

表2 外推点的外符合精度Table 2 External coincidence accuracy of extrapolation point

型。因此,通过本次实验表明:在等权条件下,非线

性Gauss-Markov模型与广义EIV模型的估计结果是一致的,验证了文献[8]中的结论。

3.2 仿真实验

假设有94个观测点,首先采用均匀分布分别在[4 172 000,4 179 000]m和[610 500,614 500]m范围内生成94个观测点的平面坐标真值,再根据式(2)生成相应点位的高程异常真值,二次曲面多项式的系数分别是:

其次,采用均匀分布分别在[0.04,0.08]m和[0.03,0.06]m范围内生成平面坐标和高程异常的中误差,再以标准正态分布随机生成平面坐标和高程异常的中误差,并与平面坐标和高程异常真值相加获得仿真观测值。上述过程重复10 000 次,但每次仿真中平面坐标和高程异常的真值及中误差一致。

均匀选择其中60个点作为拟合点,剩余34个点作为检核点,点位分布如图3所示。分别采用非线性Gauss-Markov模型和广义EIV模型对仿真数据进行求解,通过10 000 次求解的参数结果与二次多项式参数真值求解参数的均方根误差,结果见表3。图4为检核点的均方根误差序列,分别统计其平均值、最大值、最小值,统计结果见表4。

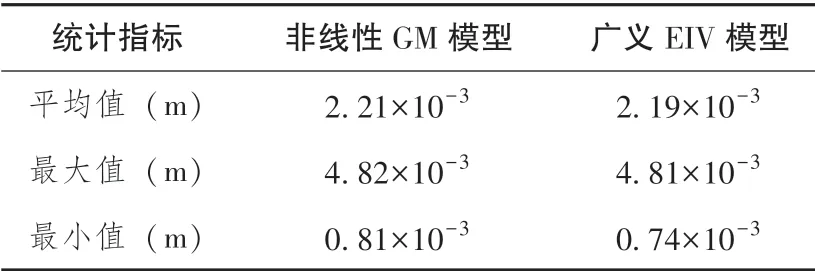
表4 检核点均方根误差统计结果Table 4 Statistical results of the root mean square error of the checkpoints

表3 多项式系数的均方根误差Table 3 Root mean square error of polynomial coefficients

由表3、表4和图4可知:(1)相较于非线性GM模型,广义EIV模型求解的二次多项式参数分别提高了16%、8%、11%、10%、6%以及13%;(2)检核点的均方根误差平均提高了3%,且从均值、最大值与最小值的统计结果来看,广义EIV模型的解算结果优于非线性GM模型。

图5为两种模型解算的时间序列,同样以平均值、最大值以及最小值为指标进行统计,结果见表5,非线性GM模型的计算效率要优于广义EIV模型,这是由于非线性GM模型未顾及系数矩阵中含有的随机误差,故其函数模型为线性模型,无需进行迭代计算,因此计算效率较高。采用广义EIV模型在一定程度可以提高参数估计的精度,但是提高的效率较小,这是由于二次多项式中的二次项系数较小,造成B矩阵的数值较小,进而导致平面坐标误差项的估值较小,因此对最终估计结果的改正较小,且相较于高程异常误差向量估值的量级相差较大。

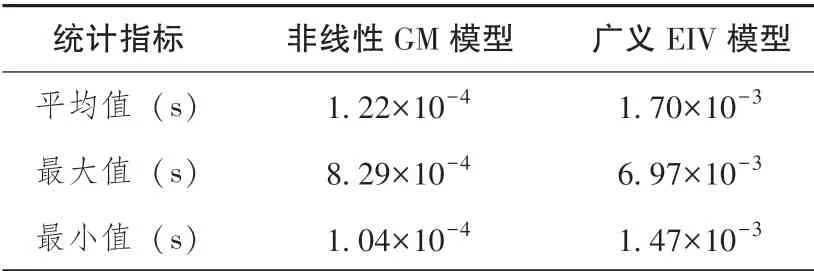
表5 运行时间统计结果Table 5 Statistics of running time

4 结论

论文针对矿区开采沉陷高程异常拟合问题,详细研究了基于非线性Gauss-Markov模型和广义EIV模型的拟合方法,并通过实测实验和仿真实验进行了验证。实验结果表明:在仿真实验中,基于广义EIV模型求解结果优于非线性Gauss-Markov模型。但实测实验结果表明两者解算结果一致且精度相当。这与文献[8]中的结论一致,即在等权条件下,Gauss-Markov模型与EIV模型的求解参数是一致的。因此,建议在实际中采用广义EIV模型,应将原始水准数据的平差结果与RTK测量结果的方差协方差矩阵作为拟合的随机模型,若方差协方差信息不甚丢失,建议直接采用Gauss-Markov模型。另外,由于矿区环境较为复杂,观测数据可能会存在粗差,因此将在接下来的工作中进一步开展基于广义EIV模型的粗差数据处理方法。