不同粗糙度下磨削表面形貌特征与仿真研究

梁瑞，成栋才，姜峰

(兰州理工大学 石油化工学院，甘肃 兰州 730050)

0 引言

磨削密封面在许多精密仪器中应用十分广泛，故研究磨削表面的微观形貌结构特征对分析界面密封、摩擦、磨损等具有重要的意义。表面形貌就像人的指纹一样蕴含着丰富的加工信息，通过这些加工信息可以预测工件表面形貌分布规律、控制工件表面质量和指导加工制造等。在工程中表面形貌分布主要分为两种，即高斯分布和非高斯分布[1-2]。这两种分布有时可以同时存在于工件中，比如，高斯分布的表面如果经历一些微动摩擦、磨损或者腐蚀之后也会呈现出非高斯分布的情况。

表面形貌的研究手段有试验和仿真两种。目前主要以试验研究为主，其特点是准确、直观，只需借助实验设备得到实验数据，对实验数据运用数理统计的方法进行处理分析就能得出结果，如PLOURABOUE F等[3]应用原子显微镜通过多尺度方法对冷轧钢表面形貌进行了定性的分析；MA B等[4]通过试验测量，在不同压下量、不同润滑条件下分析了工件表面的形貌。而仿真研究的结果具有不确定性，需要进行理论或者实验的验证才能确保结论的正确性。仿真需要建立在一定理论模型的基础上来研究，目前研究表面形貌的理论模型有蒙特卡洛模型[5]、自动回归模型[6]、随机中点位移模型[7]、神经网格模型[8]、函数序列模型[9]等，但是这些模型都是不同学者的尝试，还没有一种理论模型被学界广泛认可。

分形几何学的创立者MANDELBROT B B[10]认识到物体表面形貌非常复杂并且符合分形的几何特征，后来分形理论逐渐被引入到表面轮廓的研究中。近年来一些国内学者应用分形理论在表面接触模型的研究中做出了很多开拓性的成果[11-12]，但是对于整体分析表面轮廓高度分布的文章鲜有报道，特别是磨削表面的形貌分布具体呈现怎样的规律并不是很清楚。结合双变量W-M分形函数运用Matlab仿真可对磨削表面形貌分布特征进行深入的研究。

1 磨削表面轮廓高度仿真

1.1 不同坐标下的W-M函数

粗糙表面轮廓形貌具有随机性和无序性，因此想要准确描述粗糙表面的形貌规律，必须建立与尺寸无关的参数来描述。双变量W-M函数结合分形理论可以用于描述粗糙轮廓[13-14]，其极坐标方程为

{cosfm,n-cos[k·γn·ρ·cos(θ-αm)+fm,n]}

(1)

(2)

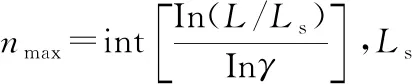
1.2 三维轮廓高度仿真

把分形参数与实际粗糙表面的表面粗糙度结合起来具有重要的现实意义。索双富等[15]用实验的方法研究了分形维数D和轮廓算术平均偏差表面粗糙度Ra之间的关系为

(3)

联立式(2)和式(3)得到Ra与Z(x，y)之间的关系如下：

(4)

为了得到随机相位下不同表面粗糙度的表面轮廓示意图，现取样本长度L=5 mm；截止长度Ls=1 nm；随机相位φm,n不同，得到的表面轮廓的示意图也略有差别。φm,n可以用Matlab中随机函数rand()与2π的乘积来实现，于是得到图1所示在磨削情况下不同表面粗糙度的三维轮廓高度的分布图，其中x轴与y轴表示采样长度。

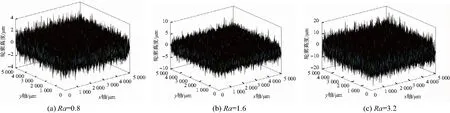
图1 三维轮廓高度分布图

粗糙度除了用Ra表示外，有时还会用Rz来表示。Rz是指在取样长度内5个最大轮廓峰高的平均值和5个最大轮廓谷深的平均值之和，称作十点平均粗糙度。在国内Rz与Ra的关系通过试验得出一个经验公式[16]：Rz=4.5Ra0.971。通过D与Ra、Rz与Ra以及二维分形维数Ds与D之间的关系，最后得到了如表1所示Ra、Ds、D、和Rz之间的对照关系。

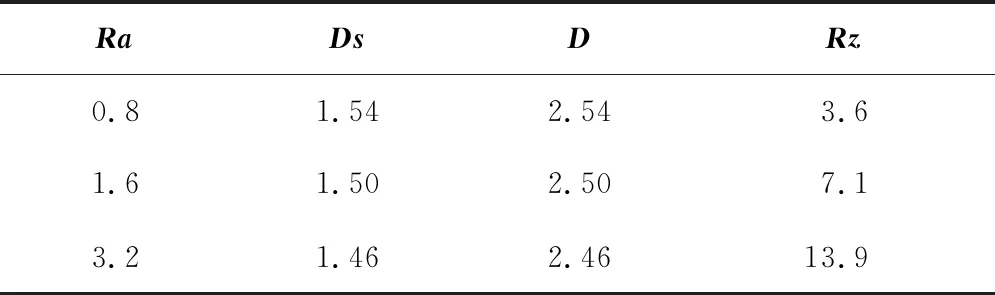
表1 Ra、Ds、D和Rz对照表

从图1中得到，当Ra为0.8、1.6、3.2时，轮廓高度的范围分别不超过4、8、16，这与表1中Rz得出的经验数值很接近，说明仿真结果能够反映实际磨削下的轮廓高度大小的范围。下面将进一步研究磨削表面轮廓高度分布的规律以及仿真结果是否能够反映实验结果。

2 磨削表面形貌分布规律

为了使研究结果更具有说服力，先通过分析磨削表面轮廓实验数据得出结果，再通过分析双变量W-M函数，从仿真数据中提取轮廓高度数据进行分析，最后把两者进行比较得出结论。

2.1 实验结果分析

从前面已经知道，粗糙表面的轮廓高度分布规律呈现高斯分布和非高斯分布两种。高斯分布又名正态分布，于1733年由德国数学家Moivre首次提出，其概率密度函数为

(5)

式中：f(x)为概率密度函数；σ为标准差；μ为均值。

为了研究磨削粗糙平面的形貌分布规律，将文献[17]中有关磨削实验的Ra为0.8、1.6、3.2的3种试样的实验数据进行Matlab软件处理，根据GB/T131—2006中对Ra及基准线的规定找到一条基准线，分析得到3种不同表面粗糙度的试样磨削表面轮廓高度分布，它们都呈高斯分布的规律，如图2所示。

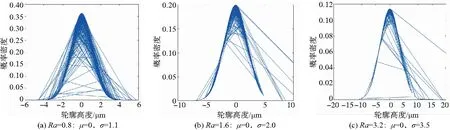
图2 实验轮廓高度分布

图2表明，3种表面粗糙度下高斯曲线的均值μ均为0，说明在数据分析过程中对基准线确定是正确的。当Ra=0.8时，σ=1.1，根据正态分布的定义，此时磨削表面的形貌高度分布规律呈标准正态分布；当Ra依次取0.8、1.6、3.2时，σ的值分别为1.1、2.0、3.5，这表明随着Ra增大磨削表面轮廓高度分布趋于分散。根据表1可知随着Ra增大，分形维数在不断减小，表面形貌趋于简单。

2.2 W-M函数分析

在双变量W-M函数中，粗糙表面服从高斯分布时，γ取1.5，且γ与D之间不存在数学关系，主要是基于表面平整度和频率分布密度的考虑，同时取非整数的目的也是为了使式(1)中空间频率呈几何级数变化的缘故，最后获得余弦叠加和表现出随机性。

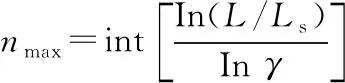
随机相位φm,n可用正态分布随机函数randn()与2π的乘积来表示。此时公式(4)简化为

(6)

公式(6)即为服从高斯分布下的W-M函数，用来描述磨削表面形貌高度分布规律。当表面粗糙度Ra取0.8、1.6、3.2时，运用公式(6)对磨削表面轮廓高度进行模拟仿真，获得不同表面粗糙度下轮廓高度的模拟仿真数据。对数据进行分析研究，得到如图3所示的磨削表面形貌高度分布图。

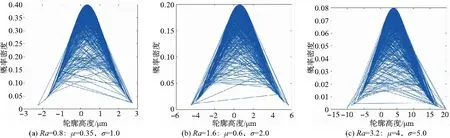
图3 仿真粗糙表面分布规律

2.3 两种分析比较

从图3中明显看到，根据W-M结果也呈高斯分布，与实验数据分析得到的结果是一致的。随着Ra的增大，标准差也在依次增大，说明磨削表面轮廓高度分布随Ra的增大越来越分散。这与分析磨削实验数据得出的结论完全一致，故今后可以运用以上仿真的方法预测任意表面粗糙度下磨削表面的轮廓高度分布情况，对密封表面的加工具有一定的指导意义。

3 结语

综上所述，根据仿真模拟得到的不同表面粗糙度下轮廓高度的大小范围和分布规律与实验数据分析得到的结论是一致的。具体有以下结论：

1)磨削粗糙表面形貌呈高斯分布；

2)随着表面粗糙度Ra的增大，分形粗糙度G逐渐增大，分形维数D逐渐减小，表面轮廓微凸体重叠数目M呈递减趋势，但是变化幅度不大；

3)Ra越大，标准差越大，表面形貌轮廓高度分布越分散。