装配应力对六维力传感器性能的影响研究

屈震龙，相立峰，李晨，王周义，戴振东

(1. 南京航空航天大学 机电学院，江苏 南京 210016； 2. 南京神源生智能科技有限公司，江苏 南京 211215)

0 引言

信息的精准、快速感知是智能化工业发展的重要保障[1]。接触过程在加工、制造、生产等行为中普遍存在。因此，利用多维力传感器来实现接触作用力的精准、快速测量在智能制造、国防工业和前沿科学等领域具有重要意义[2]。

在基于不同原理的多维力传感器中，电阻应变式的多维力传感器因兼具较好的静、动态性能和成本等优势而受到研究人员的广泛关注[3]。电阻应变式力传感器的技术核心是测量结构弹性应变来获得载荷(力或力矩)。因此，电阻应变式力传感器在使用过程中应尽可能地降低非待测载荷导致的应变来保障测量可靠性。

然而，由于受加工误差、安装定位偏差等因素影响，力传感器弹性体在与其他结构连接、装配过程中不可避免地会产生装配应力。此外，为避免使用过程中意外损害传感器内部结构和电路，通常需要对传感器弹性体进行封装。封装过程也不可避免地会导致装配应力。这些装配应力属于典型的非待测载荷，轻则引起传感器弹性体初始变形，导致其静、动态性能变化；重则导致结构破坏，造成传感器永久损伤。因此，装配应力的影响是力传感器使用过程中必须考虑的问题。

本团队在前期研究中研发了一种圆柱形电阻应变式六维力传感器，实现了三维力和三维力矩的高精度低耦合测量，并为该六维力传感器设计了专门的结构，一方面对传感器进行封装，另一方面起到力传递作用。本文通过仿真和实验分析的方法对该封装装配过程进行了研究，力图明确装配应力对其性能的影响规律，找到合适的装配方法，保证六维力传感器的性能，并为其他类型六维力传感器的研制和使用提供参考。

1 六维力传感器及其封装设计

用于本文研究的六维力传感器弹性体如图1(a)所示[4]。设计量程为Fx=Fy=±300 N，Fz=±600 N，Mx=My=Mz=±25 Nm，应变片贴片及组桥如图1(b)、图1(c)所示。根据理论设计计算：各方向空载时电桥读数应变为0，满载时读数应变分别为εFx=εFy=1073.4 με，εFz=1022.6 με，εMx=εMy=2125.4 με，εMz=1204.3 με。

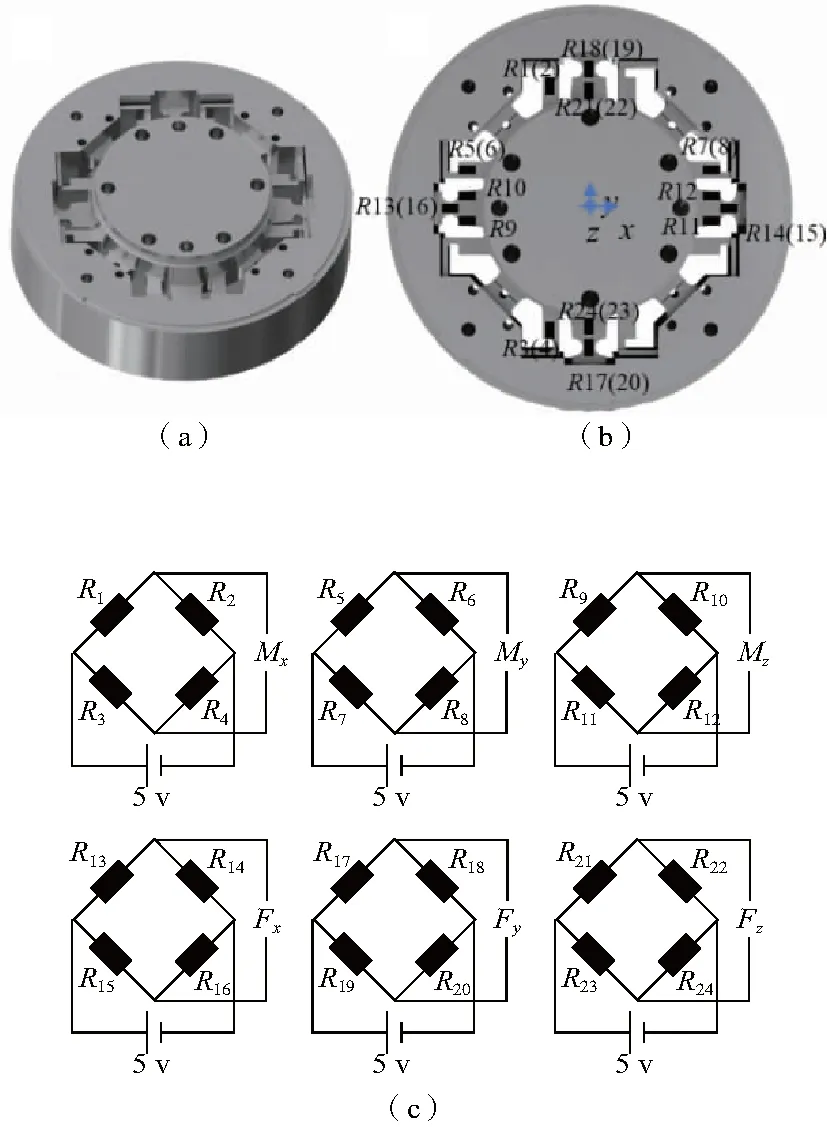
图1 六维力传感器结构、贴片及组桥示意图

六维力传感器设计的封装结构如图2(a)所示。下盖板(图2(b))不仅起到封装作用，还起到连接弹性体与基座的作用。与弹性体之间的连接必须紧固可靠，实际操作中通过8枚M5的螺栓来联接。为了保证装配定位，设计了两枚φ4的定位销。首先依次施加2.5 Nm的预紧转矩来预紧螺栓，然后依次施加5 Nm的拧紧转矩来紧固螺栓。

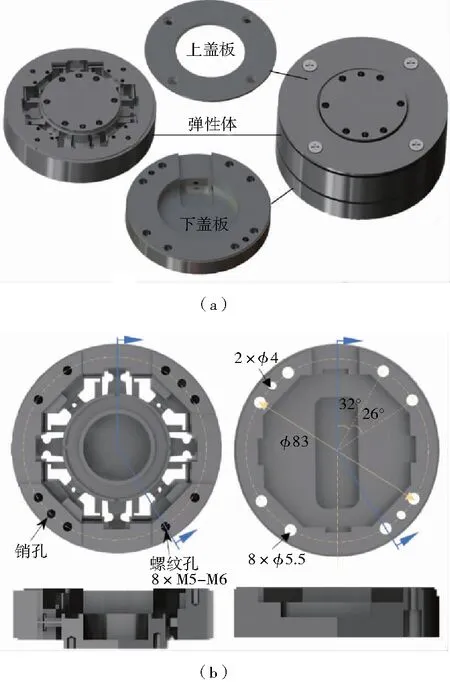
图2 六维力传感器封装设计

2 装配过程仿真分析及测试

2.1 有限元模拟

本文首先利用有限元法(Abaqus 6.14)模拟下盖板与弹性体的装配过程。分析中螺纹连接过程直接简化为力和力矩作用。螺纹夹紧力F可以用经验公式(1)来计算[4]：

(1)

式中：T是总转矩；k是转矩系数，本文选取0.2；D是螺纹公称直径。

参照机械设计手册[4]，假定下盖板与螺栓端面接触区域承受总转矩的50%，弹性体螺纹部分承受总转矩的40%，二者之间承受一对挤压力。螺纹连接的载荷可以等效为表1所示的情形。

表1 有限元分析的载荷情况

弹性体和下盖板的材料均为钛合金，弹性模量E=107.8 GPa、泊松比v=0.34、密度为ρ=4510 kg/m3、屈服强度≥895 MPa。

螺纹连接的装配过程中，装配顺序的影响是工程人员关心的重点之一。本文考虑了3种装配加载顺序：1)从销附近的螺纹孔开始，先顺时针预紧所有螺纹，然后反向拧紧所有螺纹，文中体现为2—3—4—5—6—7—8—1(预紧)/1—8—7—6—5—4—3—2(拧紧)；2)从远离销孔螺纹开始，按照对角方式预紧和拧紧螺纹，文中体现为4—8—2—6—3—7—5—1(预紧)/4—8—2—6—3—7—5—1(拧紧)；3)从销孔附近螺纹开始，按照对角顺序预紧和拧紧螺纹，文中体现为7—3—4—8—5—1—2—6(预紧)/5—1—2—6—4—8—3—7(拧紧)。有限元模型中将每一个螺纹孔的载荷设定为一个分析步。

此外，本文通过两种方式进一步探索摩擦力对装配应力的影响：①将下盖板与弹性体之间的摩擦系数设定为变量(0.1、0.2、0.3)；②改变名义接触区域的大小。

2.2 实验测试

参照有限元分析结果，本文对实际传感器进行了测试。采用自研的信号调理采集系统记录按照不同顺序拧紧螺栓时六维力传感器各个方向的输出变化，以探究装配过程的影响。

3 结果及讨论

图3示意了按照7—3—4—8—5—1—2—6(预紧)/5—1—2—6—4—8—3—7(拧紧)顺序模拟装配加载时测量Mx的电桥中各应变片(R1-R4)贴片区域及附近的应变变化规律，摩擦系数设定为0.2。图中紫色区域示意了名义接触面。灰色条示意了贴片位置(本刊黑白印刷，相关疑问请咨询作者)。根据电阻应变片的工作原理，可以认为电阻应变片测量的结果是敏感栅所在区域内应变的平均值[5]。为此，可以计算整个模拟过程中各个方向测量电桥中各个应变片的平均应变及各个电桥的读数应变，以进一步量化装配过程的影响。

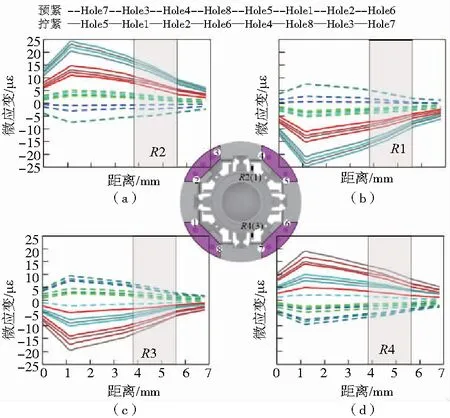
图3 一组典型的有限元分析结果

3.1 螺纹加载顺序的影响

从图4的结果可以看出，对于同一种加载顺序，不同端面摩擦系数条件下各个方向零漂的变化规律相似。此处以端面摩擦系数为0.2为例，讨论装配加载顺序的影响，端面摩擦系数的影响将在下一节中讨论。

采用第1)种加载顺序加载时传感器弹性体各方向的零漂如图4蓝线所示。预紧阶段Fx方向零漂先增加然后减小，然后又再次增加。拧紧阶段的变化过程与预警阶段相类似，最终为-44.9 με(图4(a))。Fy方向的零漂预紧阶段先增大后减小，而拧紧阶段先减小后增大。最终的读数应变零漂为理论满量程值的-0.2%(图4(b))。Fz方向零漂在整个加载过程中几乎持续增加，最终的零漂占满量程值的4.2%(图4(c))。Mx方向零漂也总体呈现出增加的趋势，加载完成后的应变零漂为13.7 με(图4(d))。My方向零漂总体上保持不变，最终结果为理论满量程值的-0.2%(图4(e))。Mz方向零漂在加载过程中波动较大，但最终结果仅为理论满量程值的0.3%(图4(f))。

采用第2)种方式加载时弹性体各方向零漂与载荷步的关系如图4橙红色线所示。Fx方向应变零漂在预紧和拧紧阶段均先增大后减小，最终为-53.8 με(图4(a))。Fy方向的应变零漂总体上几乎保持不变，仅有理论满量程值的0.5%(图4(b))。Fz方向的应变零漂随着载荷步的进行而增加到31.9 με(图4(c))。Mx方向应变零漂在预紧和拧紧阶段均先减小后增加，最终回复到理论满量程值的0.4%(图4(d))。My方向应变零漂变化规律与Mx方向相反，最终结果为理论满量程值的-0.2%(图4(e))。Mz方向应变零漂值在预紧阶段和拧紧阶段均表现为小幅增加—减小—增加。载荷步结束后的结果仅为设计满量程值的-0.1%(图4(f))。

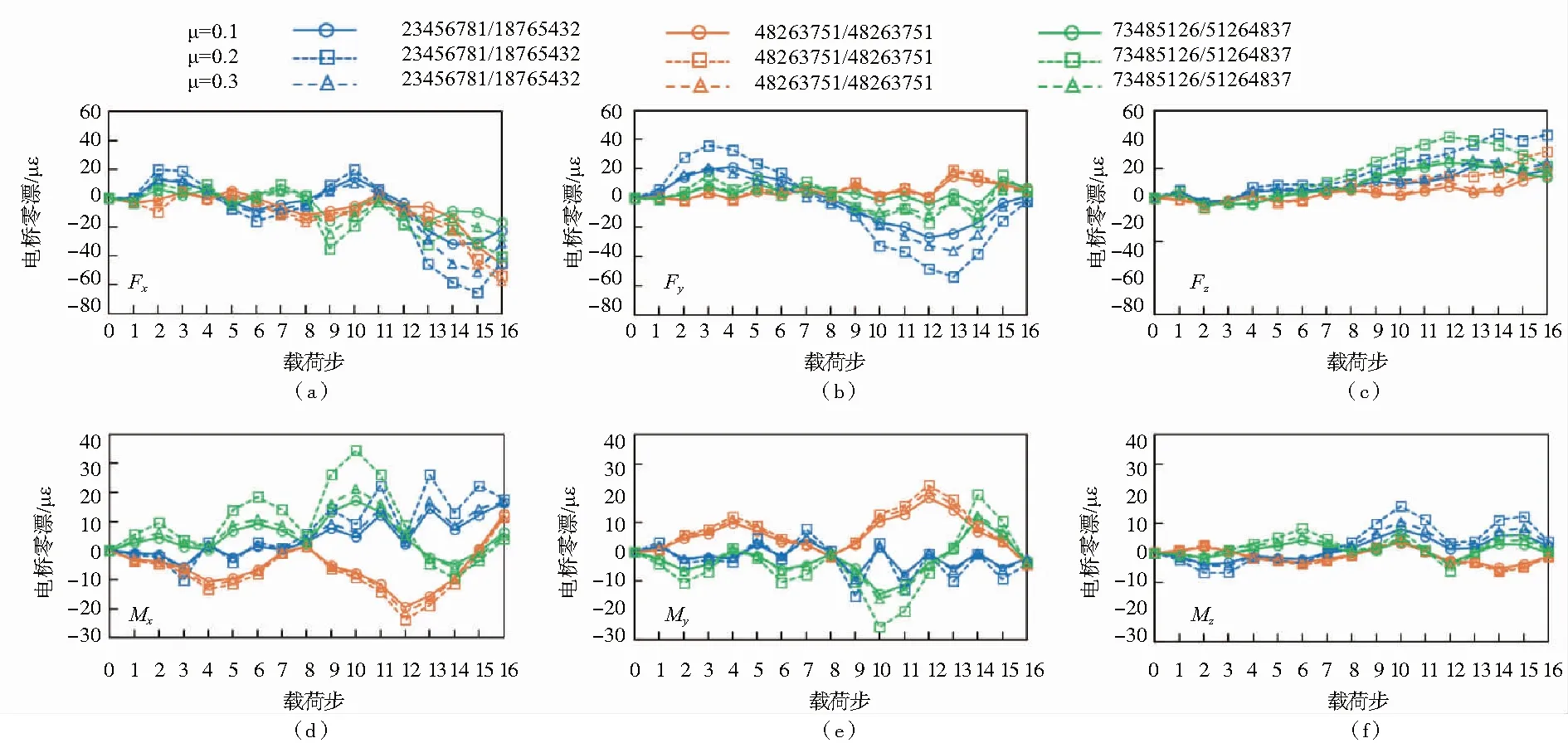
图4 不同摩擦系数条件下不同加载顺序装配有限元分析结果

采用第3)种加载顺序加载时传感器各方向读数应变的零漂变化结果如图4绿线所示。Fx方向应变零漂变化在预紧阶段和拧紧阶段具有一定的相似性，经历了“增大—减小—再增大—再减小”的变化过程，最终结果为-40.4 με(图4(a))。Fy方向应变零漂值在预警阶段总体上先增加后减小，而在拧紧阶段则先减小后增加，最终结果仅为设计满量程应变的0.4%(图4(b))。Fz方向应变零漂变化与Fy相反，最终结果为21.8 με(图4(c))。Mx方向应变零漂在预紧阶段前4个载荷步和后4个载荷步均先增加后减小，但在拧紧阶段前4个载荷步先增大后减小而后4个载荷步先减小后增大(图4(d))。My方向应变零漂的变化规律与Mx方向相反，最终的结果为-3.7 με(图4(e))。Mz方向应变零漂最终结果几乎可以忽略(0.8 με)。

上述有限元分析结果与实测结果(图6中实线)具有高度相似性。但从数值上看，实际测量的结果要比理论分析的结果略小。可能的原因包括：①有限元模型中各部分的尺寸都是理想的，而加工件可能存在一定加工误差；②加工件接触面的摩擦系数与分析中的设定值有所差异。

3种不同加载方式在载荷步进行过程中均会导致传感器各方向的零漂。但总体来说，第3)种装配加载顺序的零漂最小，第2)种次之，第1)种最大。

3.2 触端面摩擦系数的影响

图4中的实线和虚线还分别展示3种接触端面摩擦系数(0.1、0.2和0.3)条件下的分析结果。从图4的结果来看，当接触端面的摩擦系数发生变化时，各个方向的零漂变化规律相似。

在研究开始之前，曾猜测摩擦系数越大，装配应力的影响越大。然而，有限元分析的结果表明，摩擦系数为0.1时装配应力对传感器零漂的影响最小(图4实线，圆形记号)；当端面的摩擦系数增加至0.2时，3种装配顺序下装配应力导致的零漂均增加(图4虚线，方形记号)；然后，当端面摩擦系数继续增加至0.3时，装配应力导致的零漂并未继续增大，反而减小(图4，虚线，三角形记号)，但比摩擦系数为0.1时略大。这可能是由于传感器弹性体内部特殊的结构导致的。该过程涉及复杂的力学行为，还需要进一步深入研究。同时，这也启示了在实际过程中应该充分考虑装配体之间摩擦系数的影响。

3.3 接触端面大小的影响

本文还按照前述3种加载方式分别模拟了接触端面全接触和部分接触时装配情形，结果如图5所示。在此分析中，接触面的摩擦系数设定为0.2。分析结果表明，在同一种加载方式下，接触端面面积不同时传感器弹性体电桥的输出应变(零漂)理论值的变化规律相似，但总体上看，接触端面面积较小时装配应力导致的电桥零漂较低(图4虚线)。

为了验证上述理论分析结果，利用同种工艺条件和加工手段加工了两种Ti合金弹性体和盖板并进行了装配测试，结果如图6所示。测试结果表明：接触端面面积增大，零漂增大。图4和图5的结果比较发现，实际测试中传感器零漂的变化规律与有限元分析的结果具有一定的相似性，但又不完全吻合。

图5 不同接触端面大小模型装配过程有限元分析结果

图6 不同接触端面大小模型装配过程实际测试结果

仿真结果表明接触端面大时，3种方式加载装配过程导致的零漂最大可达5.8%F.S.(Full Scale)；而接触端面小时，3种方式加载装配过程导致的零漂最大为5% F.S.。而实测的结果表明，接触端面大时3种方式加载装配过程导致的零漂最大可达3.6%F.S.，而接触端面小时3种方式加载装配过程导致的零漂最大为2.9% F.S.。

在刚体研究中，摩擦力与接触面积无关。然而，本文中研究的模型材料并非是完全刚性的材料。因此，摩擦力可能会受到接触面积(接触变形)的影响。此外，本文的装配应力是由于弹性体和盖板的变形不一致导致的。在二者接触过程中，接触面会产生摩擦力，而摩擦力在一定程度上也可以看作是驱使二者变形的载荷。因此，减少接触区能够减少摩擦力的作用区。与有摩擦力时相比，这些区域上的变形会产生一定变化，最终影响传感器的输出零漂。

理论分析结果和实际测量结果的相似性表明：对于本文的多维力传感器，减小与盖板接触面的面积能在一定程度上减小装配应力的影响。

4 结语

本文通过有限元模拟和实际测试研究了装配过程对一种螺纹连接的圆柱型六维力传感器零漂输出的影响。研究发现，为了尽量降低装配应力导致的零点漂移，在装配时应该考虑如下因素：

1)有销存在时，应该尽可能地从销附近的螺纹开始加载，并按照对角原则选择加载螺纹；

2)应该充分考虑接触区域摩擦系数的影响；

3)可以通过减小接触面的方式减小装配应力的影响。