线性离散系统状态和未知干扰的递归滤波算法研究
徐迎菊,王娜,b,花玉
(青岛大学 a. 自动化学院; b. 山东省工业控制技术重点实验室,山东 青岛 266071)
0 引言
在工业和机械制造业的控制系统中,动态系统的状态是否可以被精准估计,将会影响系统运行的准确性、快速性与稳定性,如故障检测与诊断[1]、机动目标跟踪[2]、机器人技术[3]和锂离子电池荷电状态估计[4]等。与此同时,由于环境影响、模型参数选取不当、设备故障等原因,实际控制系统往往存在一些先验知识未知的干扰。针对随机系统未知干扰和状态估计问题,文献[5]提出递归状态滤波器,在没有先验知识未知干扰的条件下进行状态估计。基于滤波器存在的充要条件,文献[6]将递归滤波器设计扩展到一般的线性组合当中,得到一般线性最小方差无偏估计,并证明其与线性递归滤波器都具有最优解,保证了全局最优性。文献[4-6]仅考虑系统状态方程中含有未知干扰时对系统状态估计的影响,并且要求未知干扰的系数矩阵满足列满秩的条件。而文献[7]则提出一种新的三步迭代滤波器,可以解决系统方程中未知干扰系数矩阵不满秩时,经典滤波器无法使用的问题,然后将未知观测干扰考虑到系统量测方程中,形成新的带直通项的系统模型。文献[8]考虑了未知干扰和线性离散系统状态的同时估计问题,提出一种稳定性滤波算法,并对算法的稳定性条件及有效性进行了相应的分析。
上述研究均未考虑系统发生量测数据丢失和噪声相关的情况。在无线传感网络中,由于传感器故障、网络拥塞等现象的存在会导致测量数据的丢失。文献[9]提出用服从伯努利分布的随机序列来描述量测缺失的现象,并基于该描述对各种状态估计(滤波)和控制问题进行了有效的研究。特别是在实际工程应用中,还应将系统过程噪声和量测噪声相互关联的问题[10]考虑到系统状态估计中。因此,文献[11]提出了一种基于矩阵理论运算的理想滤波器。但是推导这种滤波算法的前提条件是量测方程中未知干扰的系数矩阵列满秩,所得结论仍具有一定的局限性。在实际应用中,系数矩阵可能不满足列满秩条件。
针对量测方程中未知干扰系数矩阵不满秩的线性离散系统,考虑其量测缺失和噪声相关的情况,本文构造了能同时估计未知干扰和系统状态的递归滤波器,通过拉格朗日乘子法将待定增益矩阵的求取转换成带约束条件的优化问题,同时运用矩阵对角理论知识直接推导计算滤波器中待定的增益矩阵,使估计误差协方差最小,满足了线性最小方差无偏估计的要求,并用数值仿真验证了该滤波算法的有效性。
1 问题描述
考虑具有未知干扰和量测缺失的一般线性离散系统:
xk+1=Akxk+Bkuk+wk
yk=δkCkxk+Dkuk+νk
(1)
式中:xk∈Rnx是系统状态向量;uk∈Rnu是未知干扰;yk∈Rny是测量输出;wk∈Rnx是过程噪声;vk∈Rny是量测噪声;δk为随机变量;Ak∈Rnx×nx、Bk∈Rnx×nu、Ck∈Rny×nx和Dk∈Rny×nu表示具有适当维数的已知矩阵。
当量测方程中出现未知干扰时,往往假定其系数矩阵是满秩的。此时假设未知干扰前的系数矩阵不满秩,rank(Dk)=rk≤nu,Dk∈Rny×nu,对Dk进行满秩分解
(2)
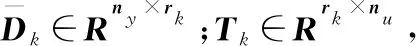
(3)
用随机变量δk来模拟量测缺失现象,并服从以下概率分布
(4)
式中π∈[0,1]是给定的标量,代表量测缺失的概率是1-π,假设所有的随机变量δk(0≤k≤N)在k中独立。
假设噪声信号wk和vk与初始向量x0是不相关的,并且噪声信号wk和vk具有以下统计特性:
(5)
式中:Rw>0、Rv>0,分别表示过程噪声协方差和量测噪声协方差;Rwv表示过程和量测噪声的协方差矩阵。上述的协方差矩阵都是已知的,δ(·,·)表示以下定义的克罗内克函数
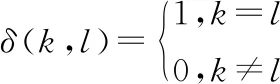
(6)
由式(5)-式(6)可以看出过程噪声wk和量测噪声vk是相关的。本文对具有相关噪声的系统,提出一种直接估计算法,简化估计值的分析过程。
2 递归滤波器的设计与研究
本文设计最小方差无偏递归滤波器,该滤波器适用于具有未知干扰、量测缺失、过程噪声和量测噪声相关的系统。与以往的设计方法不同,假设量测方程中未知干扰前系数矩阵不满秩。
为了同时估计未知干扰和状态,设计以下形式的滤波器:
(7)
(8)
(9)
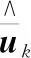
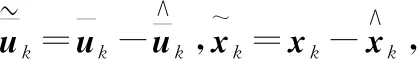
(10)
(11)
(12)
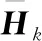
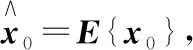
证明:由于随机变量δk与其他向量不相关,wk和vk统计特性已知,对方程(11)和方程(12)的两侧分别求期望
(13)
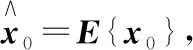
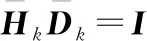
(14)
虚拟未知干扰估计误差的协方差矩阵
(15)
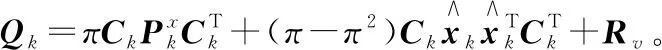
(16)
状态估计误差协方差矩阵如下
(17)
其中虚拟未知干扰和状态的估计误差协方差矩阵
(18)
(19)
其中
(20)
(21)
(22)
(23)
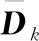
(24)
(25)
(26)
(27)
由矩阵行列式性质得
(28)
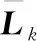
(29)
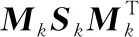
(30)
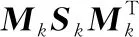
Mk=[Irk0]Uk
(31)
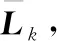
(32)
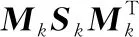
(33)

(34)
3 数值仿真分析
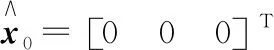
图1和图2分别是应用递归滤波器得到的线性系统状态xk和未知干扰uk的估计结果图。图1反映了系统状态的估计值跟随着真实值的变化,表现出良好的滤波性能,实现对系统状态的无偏估计。从图2可以看出,本文提出的递归滤波算法对未知干扰u2能够实现良好的估计,但是对未知输入u1没有产生估计效果,原因是对系数矩阵Dk进行满秩分解后的矩阵Tk的第一列系数全为0,导致量测值输出中没有u1的信息。
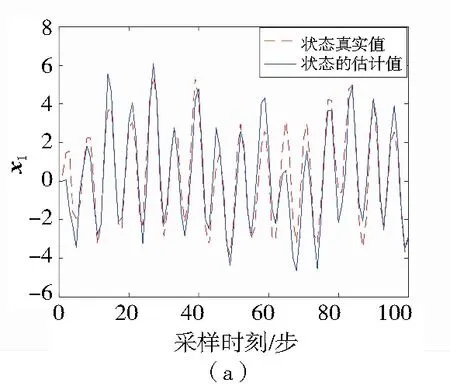
图1 状态xk真实值和估计值
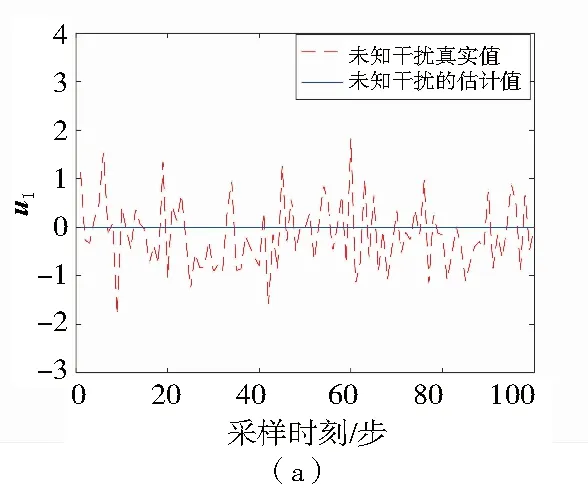
图2 未知干扰uk的真实值和估计值
4 结语
本文研究了一类含有量测缺失和相关噪声的线性离散系统状态和未知干扰同时估计问题,其中表示量测缺失的随机序列满足伯努利分布,系统内噪声相关和量测方程中未知干扰系数矩阵不满秩。提出了一种基于直接代数运算的滤波算法,该算法在满足未知干扰和线性系统状态估计无偏的条件基础上,以估计误差协方差矩阵最小化为目的,运用相关的数学理论知识获得滤波器中待定的增益矩阵,并通过数值仿真验证了该滤波算法有效性。

