超临界二氧化碳循环混合工质热力学性质研究进展

乔加飞，李 卓，廖海燕，王兵兵，刘航滔，段远源

（1.国家能源集团新能源技术研究院有限公司，北京 100024；2.清华大学热科学与动力工程教育部重点实验室，北京 100084）

2020年9月，国家主席习近平提出2030年前实现碳达峰、2060年前实现碳中和的宏伟目标。“双碳”目标下，对于清洁、低碳、安全、高效的能源利用方式的需求愈发迫切[1]。超临界二氧化碳（S-CO2）循环具有成本低、效率高、设备尺寸小、灵活性强等优点[2]，在包括核能[3]、太阳能[4]、燃煤[5]、沼气发电[6]等方面具有广阔的应用空间，主要分为闭式（间接加热式）和半闭式（直接加热式）循环。闭式S-CO2循环多采用纯CO2为工质，通过外部热源与换热器对工质加热；半闭式S-CO2循环使燃料在燃烧室直接燃烧，产生富CO2混合体系作为工质循环做功，同时结合碳捕集、利用与封存（carbon capture, utilization and storage，CCUS）技术可以捕集高纯度的CO2。

S-CO2循环的重要特点之一是循环工质跨临界或始终保持在超临界状态。与其他工质相比，CO2及其混合体系具有较低的临界参数，易达到超临界状态，具备黏度小、密度大、可压缩性小等一系列优点，因而适用于多场景的动力循环。对于闭式循环系统，Liu等人[7]、Guo等人[8]提出引入CO2混合工质，调整工质临界参数，实现不同组元的优势互补。此外，结合富氧燃烧技术的半闭式S-CO2循环，由于其高效和低碳的特性，也越来越受到研究者的重视，目前已提出多种循环方式，如半闭式富氧燃烧联合循环（semi-closed oxy-fuel combustion combined cycle，SCOC-CC）循环[9-11]、E-MATIANT循环[12]、Allam循环[13]等。对于这些循环的深入研究和工程应用，均需要深刻认识CO2及其混合体系的热力学性质。

结合闭式S-CO2动力系统的设计需求，杨富方等[14]综述了CO2在循环范围内的实验与模型研究现状，认为已有多参数状态方程[15]可在一定的温度压力范围内准确描述CO2纯工质的热力学性质，但在近临界区的定性和定量表现不够理想，可采用跨接方法[16]改进其表现。何欣欣等[17]以S-CO2循环为应用场景介绍了CO2热物性方程研究进展及应用，推荐使用GERG-2008模型[18]计算CO2热力学性质。针对CO2混合工质，Li等人[19-20]围绕CCUS技术介绍了CO2混合体系实验及理论研究情况，而在半闭式S-CO2循环设计关注的组分、温度、压力范围内，缺乏对混合工质热力学性质的评估。混合体系的热物性并非纯工质热物性的线性加权，当组元性质差异较大时，非理想性更突出，其理论描述也需要结合特定混合规则，构建合适的热力学模型。

对此，本文分析了CO2混合工质热力学性质实验数据和理论模型的研究现状，并根据半闭式S-CO2循环研究需求，指出现有实验数据和模型研究的不足及发展方向。

1 典型系统和工况

不同于闭式循环，半闭式S-CO2循环工质在燃烧室内被直接加热，通常透平进口温度更高，以实现更高的热效率。图1为简单回热半闭式S-CO2循环系统示意。循环中，压缩机出口处的工质温度和压力略高于CO2纯工质的临界点，以防止混合体系发生液化，影响系统的安全稳定运行[21]。压缩后，工质与由空气分离器制备的O2混合后进入回热器吸热，然后在燃烧室中与燃料反应吸收热量；在部分循环设计中，工质与O2也会直接在燃烧室中混合。高温高压的混合工质膨胀做功后，在回热器内放热，随后在冷凝器，混合工质中的水被分离，从而获得高纯度的CO2，其中，燃烧产生的CO2被储存，其余作为工质进入压缩机继续循环，保证循环过程中CO2工质量恒定。

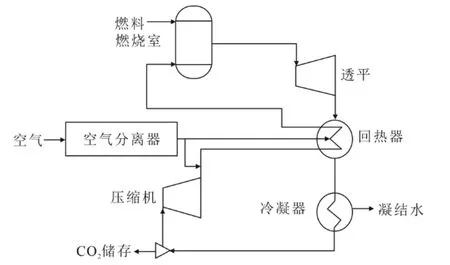
图1 半闭式S-CO2循环示意Fig.1 Schematic diagram of semi-closed S-CO2 cycle

与闭式S-CO2循环系统相同，半闭式S-CO2循环系统的工质会经过CO2的近临界区和高温高压区，临界参数、气液相平衡、密度、比热容、声速等热力学性质的变化对热力过程与系统设计、优化及运行稳定产生较大影响。此外，由于涉及混合体系，明确循环所关注的工质组成和CO2含量也非常重要。表1列出了部分学者研究的半闭式S-CO2循环关键温度压力及组分参数，表2列出了对于循环关键节点计算的工质组分，混合工质主要组分为CO2、O2、H2O，还混有摩尔分数均不超过2%的N2和Ar。其中，O2组分峰值从回热过程到进入燃烧室前呈现低温高压（压缩后的CO2与O2混合）及高温高压（回热后）的特点。H2O是燃烧产物，其组分峰值出现于燃烧室后，呈现高温高压（燃烧后）及高温低压（膨胀做功及回热后）的特点。由于N2与Ar化学性质稳定，在循环过程中将作为杂质始终存在。在压缩机进、出口处，混合体系与纯工质近似，仅含有极少杂质，因此不在本文重点研究范围内。

表1 半闭式S-CO2循环最高参数Tab.1 The highest parameters of semi-closed S-CO2 cycle

表2 半闭式S-CO2循环关键组分Tab.2 Key components of semi-closed S-CO2 cycle

综上，CO2摩尔分数超80%的混合工质在半闭式S-CO2循环中经历了从CO2临界点到最高温度1 400 ℃、压力40 MPa的状态变化，因此需要在广阔的温度压力范围内掌握工质准确可靠的热力学性质。由于高温高压的工质性质偏离理想气体规律较远，因此该多元混合体系不能视为理想气体混合物，需要慎重考虑不同组元之间的相互作用。针对S-CO2循环工质的特殊性，要建立可靠的理论模型，需要CO2与其他组元，特别是H2O和O2的二元交互系数，并使用包含多组元的实验数据进行验证。因此，本文将重点关注含CO2的二元与多元体系实验与理论研究现状，并给出研究建议。

2 实验研究现状

2.1 临界性质与饱和性质

纯净物的临界点为气液共存的最高温度和压力状态。混合体系不仅增加了组分变量，使系统自由度上升，其真实临界轨迹线也更复杂。对于混合物的热力学性质，采用混合规则计算得到的临界参数，例如最简单的是将不同组元临界温度以摩尔分数为权重线性加和的Kay规则[31]，得到的并非真实的临界轨迹线。

图2展示了CO2混合体系临界性质的实验数据分布，根据Abdulagatov等人[32]的研究，在p-T图上，CO2+O2[33-36]与CO2+N2[35-38]体系的临界特性表现为上凸曲线，CO2+Ar[32]体系在低Ar摩尔分数时表现为趋近线性，而CO2+H2O[39-42]体系的临界性质表现则较为复杂，其临界曲线不连续且向超高压方向延伸。对于S-CO2循环，N2与Ar的临界温度与压力均低于CO2，但杂质的引入会增加混合体系的临界压力，在系统循环设计时需格外注意。目前对CO2+H2O体系的临界性质研究还很不充分。

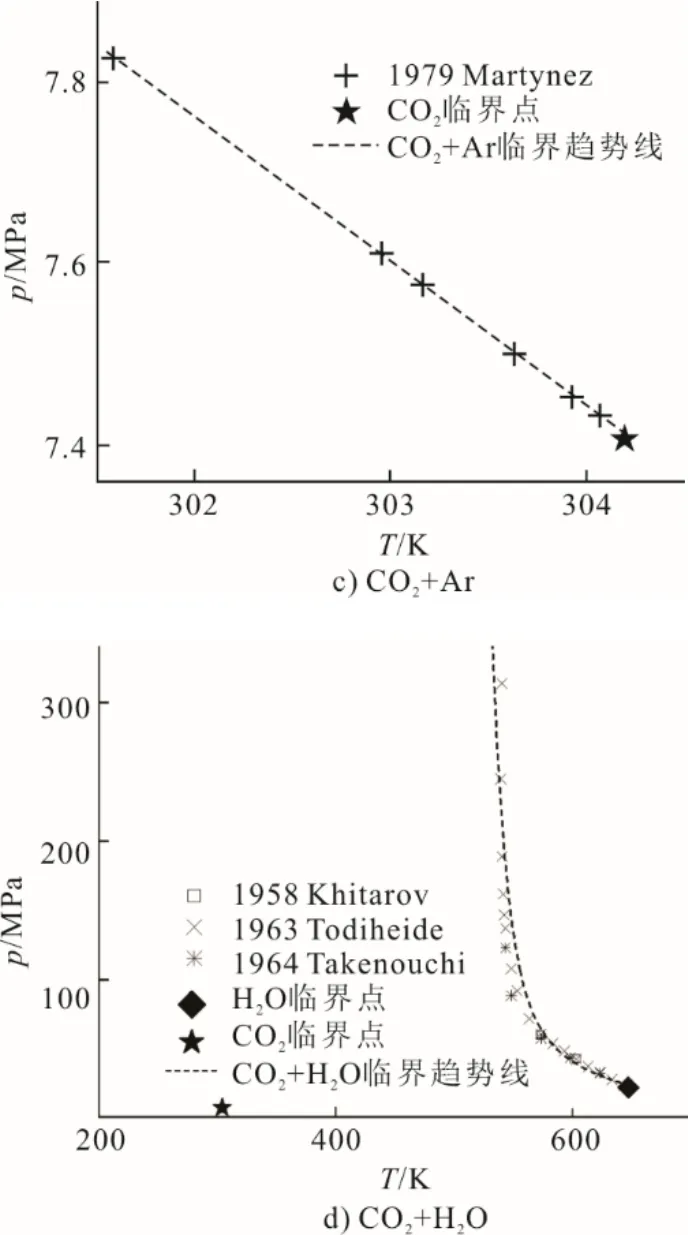
图2 CO2混合体系临界性质实验数据分布Fig.2 Distribution of experimental data on critical properties of CO2 mixtures

气液相平衡（vapour-liquid equilibrium，VLE）性质描述的是混合工质气液两相达到平衡时的温度T、压力p和气液两相组分yi、xi之间的关系，是混合体系最基本的平衡性质之一。混合体系的压力并非简单地随组分摩尔分数呈线性变化，多元体系的相平衡情况更加复杂[43]。

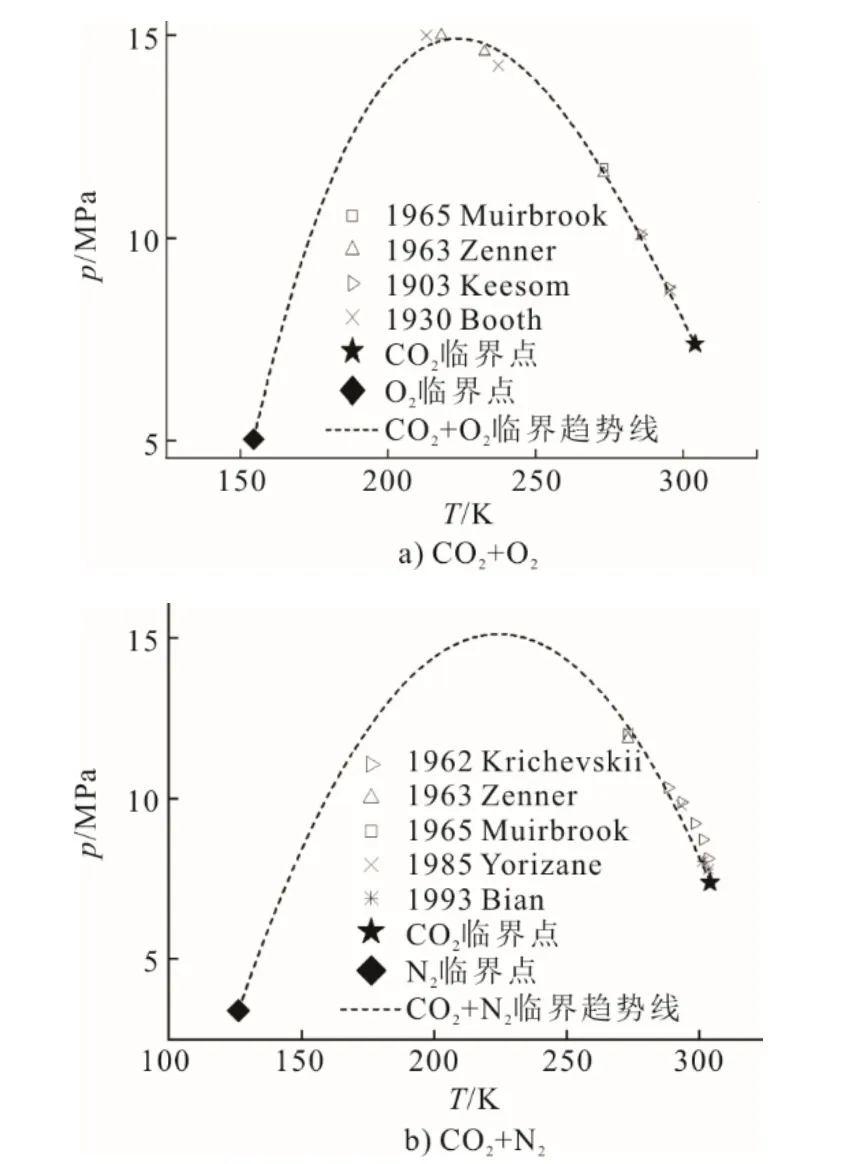
图3展示了气液相平衡实验数据在p-T图上的分布。由于其余组元临界温度压力远低于CO2，故在循环范围内只有CO2+H2O的气液相平衡数据。

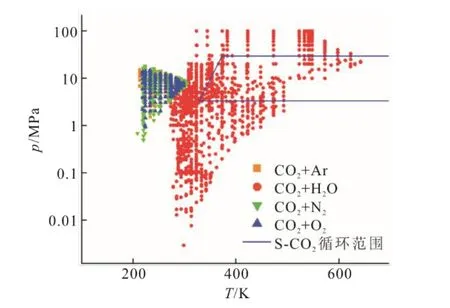
图3 CO2混合体系气液相平衡实验数据分布Fig.3 VLE experimental data distribution for CO2 mixtures

图4展示了CO2气相摩尔分数大于75%的CO2+H2O混合体系气液相平衡数据在p-T图上的分布情况。目前尚无针对S-CO2循环工质开展的近临界区域相平衡研究，但基于CO2的超临界萃取[44]、超临界水氧化技术[45]、碳捕集封存（carbon capture storage，CCS）及石油工业[46-49]等背景的CO2+H2O体系相平衡研究实验数据较为丰富。未来应开展更多CO2+H2O体系的相平衡实验，并获得其他体系的相平衡数据，以提升混合体系状态方程的精度。

图4 CO2+H2O体系气液相平衡实验数据分布(x(CO2)>75%)Fig.4 VLE experimental data distribution for CO2+H2O mixtures (x(CO2)>75%))

2.2 单相区密度、比热容与声速

混合物的单相区密度，又称为pvTx性质，是最基础的热力学性质之一，对工质的压缩、流动和膨胀过程均有重要影响。图5展示了含CO2体系的pvTx实验数据分布。可以看到，含CO2的三元及以上体系的pvTx实验数据非常稀少。对于CO2+N2+O2三元体系，仅有Muirbrook等人[35]于1962年测定的34个数据点，温度压力范围覆盖273～298 K和0.1～10.6 Mpa，尚未达到S-CO2循环所关注的温度范围。对于CO2+N2+Ar三元体系，Yang等人[50]采用目前密度测量精度最高的磁悬浮密度计法获得了323.15～423.15 K、3～31 MPa的富CO2体系的150个数据点，测量不确定度在0.2%以内。而对于CO2+N2+O2+Ar四元体系，仅有Nazeri等人[51]使用振动管密度计测定的43个数据点，温度压力范围覆盖273～423 K和1.5～10.6 MPa，x(CO2)=0.898 3，气相测量数据不确定度为1%。对于温度高于423 K的区域，仅有CO2+N2与CO2+H2O体系有少量实验数据，而其余二元或三元体系均缺乏实验研究。大量实验数据集中于低CO2摩尔分数的区域，包括CO2在水中的溶解度实验[52-56]，以及CCS技术中低CO2摩尔分数体系[57]的研究。而在S-CO2循环范围的实验数据，特别是重点关注的CO2+O2以及CO2+H2O实验数据较为缺乏。

图5 CO2混合体系pvTx性质实验数据分布Fig.5 Experimental data distribution for pvTx property of CO2 mixtures

Kunz等人[58]对与天然气相关的混合体系进行评估时，指出使用磁悬浮密度计法测量的数据代表了pvTx实验数据的不确定度下限水平，约为0.1%。在S-CO2循环涉及的体系中，Yang等人[50,57]、Souissi等人[59]、Mondejar等人[60]采用此方法进行了测量，其可靠性应受到重视。由于实验管路和实验设备的限制，磁悬浮密度计法目前较难测量CO2+H2O的相关体系，导致该体系的pvTx(y)实验精度受到限制。近年来，纯氧燃烧结合S-CO2循环技术越来越受到热物性实验研究者的关注，数据空白最严重的CO2+O2体系也陆续有新的实验开展[61-62]，Park等人[63]还专门开展了面向S-CO2循环需求的物性实验研究。

比热容和声速实验数据会影响理论模型在S-CO2循环重点温度压力范围的精度，也会作为参数参与循环的设计与优化。对于CO2纯工质，比定压热容cp和比定容热容cv在临界点趋于无穷大；声速w在临界点则趋于0[14]。由于实验数据存在大量空白，目前对混合体系的比热容与声速缺乏清晰的认知。目前尚无比定容热容的实验数据，仅有Bishnoi等人[64]测定的CO2+N2体系在313～363 K、0.2～16.5 MPa下的比定压热容数据。此外，Barbero等人[65]和Hnědkovsky等人[66]分别在常温和高温高压下测量了CO2水溶液的表观比热容，以研究非电解质稀溶液的比热容表现，但由于采用了不同的表观体积与表观比热容定义，对S-CO2热力学性质的实验数据库不具有参考价值。对于声速，CO2与O2[67]、N2[67-69]、Ar[67,70]的二元混合体系均有实验数据，其中Wegge等人[70]使用球共鸣法测量得到了CO2+Ar体系的声速数据，此方法也被Kunz等人[58]认为是最精确的声速测量方法之一，不确定度小于0.1%。在温度高于500 K的区域，缺乏关于CO2混合体系的比热容与声速的实验研究。CO2混合体系声速与比定压热容实验数据分布情况见图6。

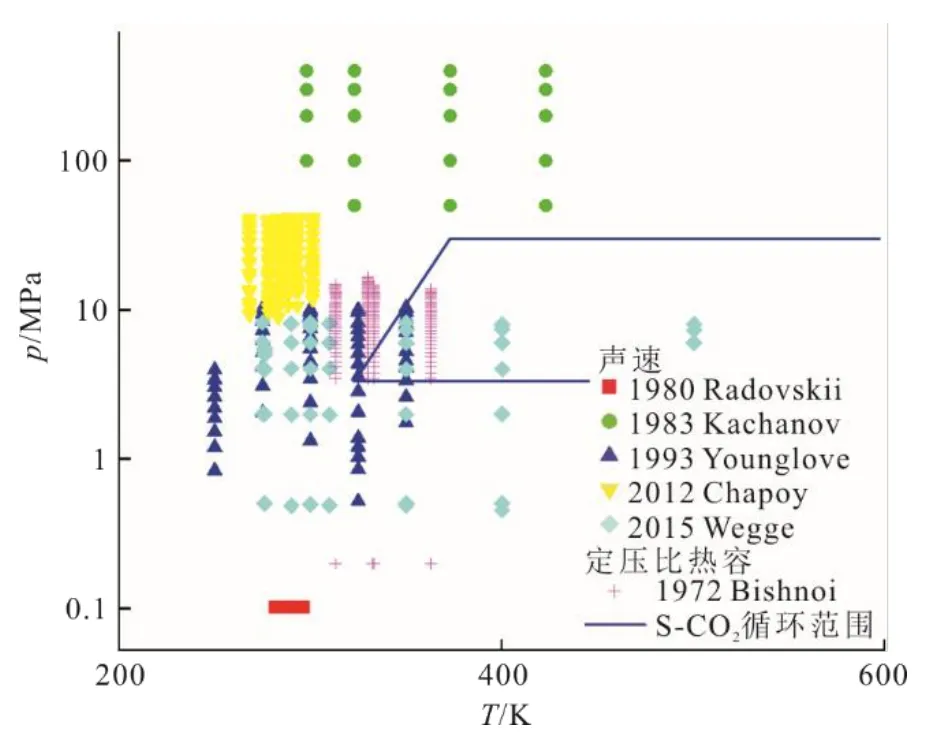
图6 CO2混合体系声速与比定压热容实验数据分布Fig.6 Experimental data distribution of w and cp for CO2 mixtures

表3汇总了现有密度、比热容与声速的实验研究现状及研究建议。

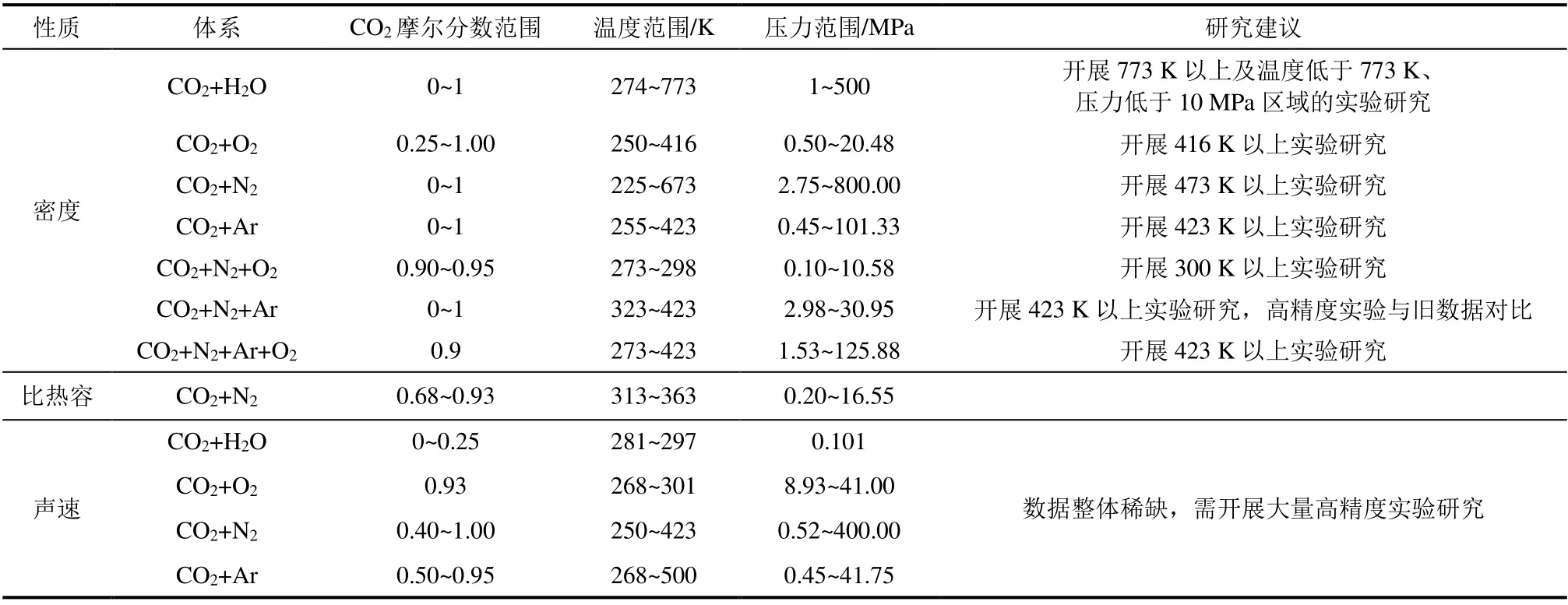
表3 CO2混合物密度、比热容与声速研究现状及研究建议Tab.3 Experimental data description and research recommendations of theomodynamic properties of CO2 mixtures

总之，对S-CO2循环，当前含CO2混合体系的pvTx、比热容和声速实验数据较不充分，在高温区存在大量数据空白，同时CO2+H2O与CO2+O2的实验数据数量与精度均未满足需求。针对S-CO2循环需求，对于单相区密度应重点关注所有二元及多元体系，特别是当前尚无实验数据体系的400 K以上区域，以及CO2+H2O体系在10 MPa以下区域的密度；对于比热容与声速，则需要对全部二元及多元体系开展更多实验研究，以填补现存的大量数据空白区域。

3 状态方程研究现状

状态方程是计算与导出工质热力学性质的理论模型，是S-CO2循环进行系统设计与优化的基础。最简单的状态方程是理想气体状态方程，仍有学者采用此方程对半闭式S-CO2循环进行计算[71]。适用于S-CO2循环相关计算的状态方程主要分为半理论方程和多参数方程。表4展示了近年来部分学者对S-CO2循环开展研究时采用的热力学模型。

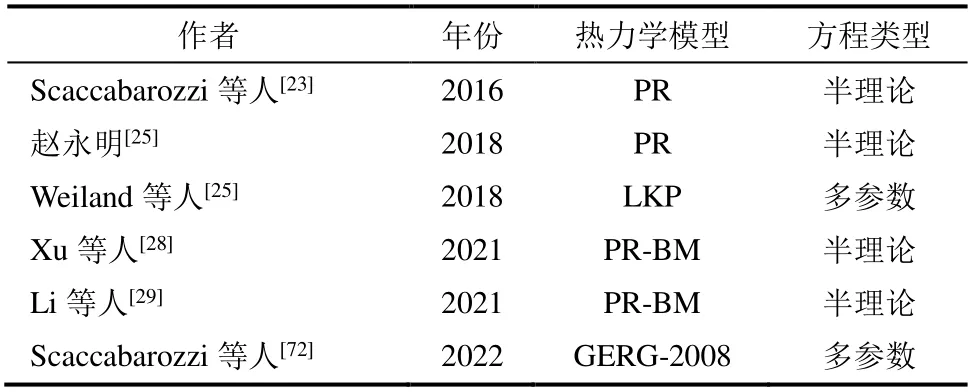
表4 研究半闭式S-CO2循环使用的状态方程Tab.4 Equations of state used in studies of the semi-closed S-CO2 cycle

半理论方程的构建基于一定的理论基础，利用数据对有理论背景的参数进行优化，方程一般适用于多种物质，有较好的外推性能，且可以从纯净物推广到混合物而不对方程形式有巨大改变。目前，较多应用于S-CO2循环计算的是立方型方程，如PR、SRK方程[73]，PR方程形式如下：

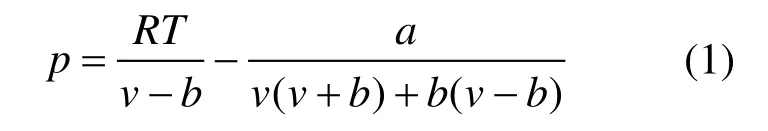
SRK方程形式如下：

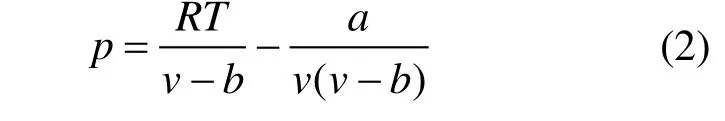
式中：p为压力，T为温度，v为比体积，R为气体常数，a、b为与温度相关的系数。

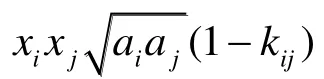
多参数状态方程是一类基于大量实验数据构建而成的热力学模型，通常含有大量无明确物理意义的参数，利用实验数据优化参数与函数形式，可以在实验数据覆盖的范围内精确复现实验数据，但外推预测性能较差。对于CO2的混合体系，目前应用最广泛的是LKP方程[75-76]、GERG-2008模型[18]和EOS-CG模型[77]。

LKP方程的构建基于对比态原理，表达形式为：

式中：下标r代表对比参数，bi、ci、di、β、γ是可调参数。对于混合体系，应用混合规则，调节相互作用系数，即可计算热力学性质。

GERG-2008模型是对GERG-2004模型的改进，以Helmholtz函数为显式进行表达：

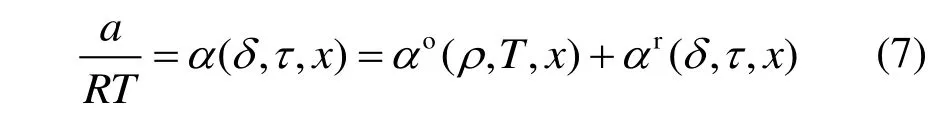
式中：α为Helmholtz函数，上标o代表理想气体项，上标r代表剩余项；δ、τ、x为对比密度、对比温度与摩尔分数。利用实验数据对剩余项进行拟合，即可高精度复现实验数据。EOS-CG方程在GERG-2008模型的基础上作进一步优化，将适用气体种类从18种缩小到6种（CO2、O2、N2、H2O、Ar、CO），几乎与S-CO2循环所需气体组分完全相同。

针对S-CO2循环的研究需求，各类方程精度有所不同。Chowdhury等人[78]对比了PR、LKP和理想气体状态方程对S-CO2循环燃烧过程的计算结果，认为在高温高压条件下，LKP方程计算效果更好，适合超临界系统的计算。Scaccabarozzi等人[24]使用Aspen Plus软件内置的二元交互系数对比了PR、SRK、BWR方程后，认为PR方程计算半闭式S-CO2循环更准确，特别是CO2+H2O体系，密度性质相对偏差小于2%，而SRK方程则在计算CO2+O2体系时更准确。White等人[79]则对CO2+H2O体系展开了重点研究，推荐LKP方程作为计算工具。Li等人[80]研究认为，PR方程计算CO2+N2与CO2+Ar体系的整体精确度优于SRK方程，特别是液相区域（PR：2.07%，SRK：5.42%）。Mazzoccoli等人[81]对比了常温下多种状态方程对富CO2体系的热力学性质计算，认为LKP方程和GERG模型计算表现相对较优，而PR方程在立方型方程中表现最好，对密度性质的预测偏差普遍在1%以上。对于当前精度最高多参数状态方程的GERG-2008和EOS-CG，其声称在有效范围内pvTx性质的不确定度在0.1%～1%，然而其扩展有效温度范围为700 K，远低于S-CO2循环的最高温度。此外，Lozano-Martín[61]、Yang[50,57]、Nazeri[82]、Souissi[59]、Wegge[70]等人的研究表明，GERG-2008和EOS-CG与实验数据的偏差往往会超出其声明的不确定度，对于富CO2体系还会出现偏差增大的现象。需要注意的是，GERG-2008和EOS-CG模型在拟合参数时，由于实验研究的空白，没有使用CO2+O2体系的pvtx实验数据，使用CO2+H2O体系pvtx实验数据的最高温度也没有超过700 K。因此，使用GERG-2008和EOS-CG模型进行S-CO2循环的计算时，必须考虑其对特定组分以及超出有效温度压力范围计算的可靠性。根据当前状态方程的研究现状，对于温度低于700 K的循环部件研究，推荐使用当前计算精度最高的GERG-2008和EOS-CG模型；而当温度超过当前实验数据的覆盖范围时，应当优先使用具有理论背景的PR、SRK等立方型方程或LKP等维里型方程。特别地，针对重点组元体系，推荐使用LKP方程计算CO2+H2O体系物性，PR方程计算CO2+O2体系物性。此外，如果有基于前述数据空白所开展的实验研究，得到了新的二元交互系数，或者对现有经验模型的外推模型，应当及时对现有模型进行更新。

整体而言，目前广泛应用于CCUS技术的高精度多参数状态方程并不能很好地适应S-CO2循环的高温高压计算需求，而已经有充分研究成果的立方型状态方程的精度并不够高。因此，状态方程研究除了依靠新的实验数据对已有方程进行优化外，还应考虑充分利用现有数据与物质共性规律，如构建S-CO2循环专用的基于深刻理论研究的截断维里型状态方程，以达到对现有实验数据的良好外推效果。

4 结论与展望

1）相比其他性质，CO2混合体系气液相平衡数据较为丰富，但针对S-CO2循环研究需求，CO2+H2O体系近临界及高温区域气液相平衡的实验研究还较缺乏；CO2的部分二元体系及多元体系的pvTx实验数据相当缺乏，全部体系均无超过800 K的pvTx实验研究。

2）缺乏对于CO2混合体系不同组分与温度压力条件下的比热容与声速实验研究。

3）目前广泛应用的半理论与多参数状态方程在气相区与超临界区存在精度及有效温度压力范围不够的缺陷，这是由混合体系高温实验数据缺乏造成的，应考虑采用能够充分利用现有数据并具有良好外推性能的状态方程形式。