计及电动汽车的有源配电网新能源消纳两阶段调度策略

李清涛，卢 钺，刘 洋，刘 顺，刁晓虹，张元星，马 强

（1.国网北京海淀供电公司，北京 100000；2.中国电力科学研究院有限公司，北京 100192）

随着新能源技术的不断发展，以风力和太阳能发电为代表的新能源在电网中的渗透率越来越高，高比例新能源发电已成为全球广泛关注的未来电力市场场景[1-2]。在“十四五”建设中，我国提出要保证集中式和分布式新能源同时开发，着力扩大光伏和风机的发电规模[3]。在这样的大背景下，新能源并网比例将不断提高，但因其间歇性和波动性的特点，大规模接入电网势必会给电网安全可靠运行带来巨大挑战。

制定行之有效的调度策略以提高新能源消纳量已成为现今研究的热点问题，文献[4]为提高新能源消纳的有效性，提出了一种考虑负荷灵活协调调度的配网新能源消纳策略，构建了考虑灵活负荷协调调度的新能源优化消纳模型，促进园区能源就地消纳。文献[5]提出了一种考虑高比例新能源消纳的多能园区日前低碳调度模型，同时在建模时充分考虑园区能源耦合设备与电动汽车充电方式的影响。文献[6]结合电价和储能2种灵活可调节方式，提出一种电价和储能共同优化调度策略，构建园区电价和储能2层协调优化模型以促进新能源就地消纳。文献[7]基于Stackelberg动态博弈理论，提出一种以配电网侧为主体、负荷侧为从体的主从博弈模型，建立以配电网运行成本最小及风电消纳最大、负荷侧用户电费最低为目标的主从博弈经济模型。上述文献均为单一微网或园区内的新能源消纳策略，而相邻微网或园区间的互济互补可大大增大消纳能力提高系统的稳定性，文献[8]基于“端-边-云”架构，考虑园区中相邻供能子系统之间的电、热、气互济互补，建立了园区多个能源系统协调优化模型。文献[9]考虑电网结构复杂性与能源设备多样性，为减小多个优化控制器的计算压力，提出一种基于交替方向乘子法（ADMM）的分布式双层优化调度求解方法。文献[10]在微网运行安全的环境下，构建了微网集群的双层优化调度模型，微网集群经济效益提升的同时保证新能源消纳的高效性。文献[11]把管理系统分为内外2层，内外2层的设备资源能量协调互补，提出了微网集群双层系统的日前能量管理模型，所得分层管理模式下的微电网群运行成本更低，新能源消纳量更高。文献[12]把配网协调能力最大化作为优化目标，优先考虑配网然后优化微网，采用双层控制结构进行整体优化调度。保证配网经济性运行的同时，降低配网与主网的交互功率，从而提升新能源的利用率。文献[13]通过建立与分析园区内各能源子系统的数学模型，以园区系统运行成本最低为目标建立日前优化调度模型，实现多设备之间的能源互补。

上述考虑配网区域间电能互补互济提高新能源消纳的研究中，在建模方面缺少电动汽车群体，现今电动汽车因其响应速度快且灵活的特点，通过对其合理的调度可有效消纳系统过剩新能源；同时现今有源配网分布式调度策略多为日前策略，但新能源具有随机性的特点，日前预测误差较大，这使得系统鲁棒性较差，所制定调度策略难以实际应用；为此，本文提出一种计及电动汽车的有源配电网两阶段分布式新能源消纳策略，在日前阶段考虑不同区域内电动汽车与用能设备，配网区域间能量互济互补，以提高系统新能源消纳量；日内阶段考虑源荷预测误差，引导电动汽车及储能系统响应，保证跟踪日前计划并实现第二阶段新能源消纳。

1 两阶段优化调度框架

本文两阶段优化调度框架如图1所示。

图1 两阶段优化调度框架Fig.1 Two-phase optimization scheduling framework

由图1可见，第1阶段为日前阶段，以1 h为调度间隔，在建模时考虑不同区域电动汽车参与响应能力，保证配网经济运行的同时，降低配网与主网的交互功率，从而提升新能源的利用率；在日前阶段求解时，将原问题进行分解，利用同步型ADMM对所建立第1阶段消纳模型进行分布式求解，以缓解集中优化带来的计算压力。第2阶段为日内阶段，以15 min为时间间隔，4 h为周期进行滚动优化，考虑日前阶段源荷预测的偏差，在日内阶段引入储能系统，并发挥电动汽车群体的灵活性进行联络线之间功率的调整，以实现第2阶段新能源消纳，消除日前阶段预测偏差，并跟踪日前阶段调度计划。

2 日前优化模型

2.1 目标函数

为减少向上级电网购电，促进各区域间新能源消纳量，并兼顾自身运营成本，设置日前优化模型目标函数为：

式中：Pgird(t)为与电网交互功率；PDG(t)为柴油发电机功率；c为柴油发电机发电成本；CGird+(t)、CGird-(t)分别为与上级电网交互价格；γ1、γ2均为相应目标系数。

2.2 储能设备约束

通过在系统中增设储能设备可提高系统的稳定性，同时储能具有快速性可使在日内阶段较好地跟踪日前调度计划，所建立储能模型为：

式中：Pmax,si、Pmin,si分别为储能系统充放电功率上、下限；ηc、ηdisc分别为储能系统充、放电效率；SSOC,max、SSOC,min分别为储能系统荷电量上、下限。

2.3 空调模型

基于一阶等值热力学模型，对空调模型建立如下约束：

式中：ρ、C分别为室内空气的密度、热容；V、CVESS分别为住宅体积、空调制冷/热量；Awin、Awall分别为住户i的外窗、外墙面积；kwin、kwall分别为外窗、外墙传热系数；Tout(t)为t时刻住宅室外温度；PVESS,max为空调出力上限；CCOP,VESS为空调制冷/热能效比；Tmax、Tmin分别为所设置温度上、下限；式(6)为空调的出力功率上下限约束，式(7)为空调制冷/热量等式，式(8)为空调虚拟储能调节带宽。

2.4 电动汽车模型

2.4.1 电动汽车聚合模型

考虑电动汽车群体数量庞大，具有较大的可调度潜力和灵活快速的特点，以第i辆电动汽车运行域（图2）为例进行说明。

图2 单体电动汽车运行域Fig.2 The operating domain of a single electric vehicle

由图2可见，电动汽车i在tin时刻接入电网，沿AB边进行最大功率充电，沿AD边进行最大功率放电，可建立充放电功率约束：

式中：PEV,i(t)为电动汽车功率；PEV,max、PEV,min分别为电动汽车功率上、下限。

图2中，BC边为电动汽车电量上限，DE边为电动汽车电量下限，CF边为电动汽车离开时车主可接受电量范围，EF边为电动汽车强迫充电曲线以达到CF边界。可建立如下约束条件：

式中：Ci为第i辆电动汽车电量；SSOC,EV,last,i为电动车结束充电时电量。

2.4.2 电动汽车出行规律模型

美国交通部针对全美家用汽车的行驶特性进行了数据统计，并对数据进行归一化处理，通过极大似然估计，近似地认为用户最后返程时间满足正态分布，其分布函数为式(13)；基于蒙特卡罗对配网不同区域内办公、居民区的电动汽车出行分布函数进行随机抽样，以模拟电动汽车随机出行规律。

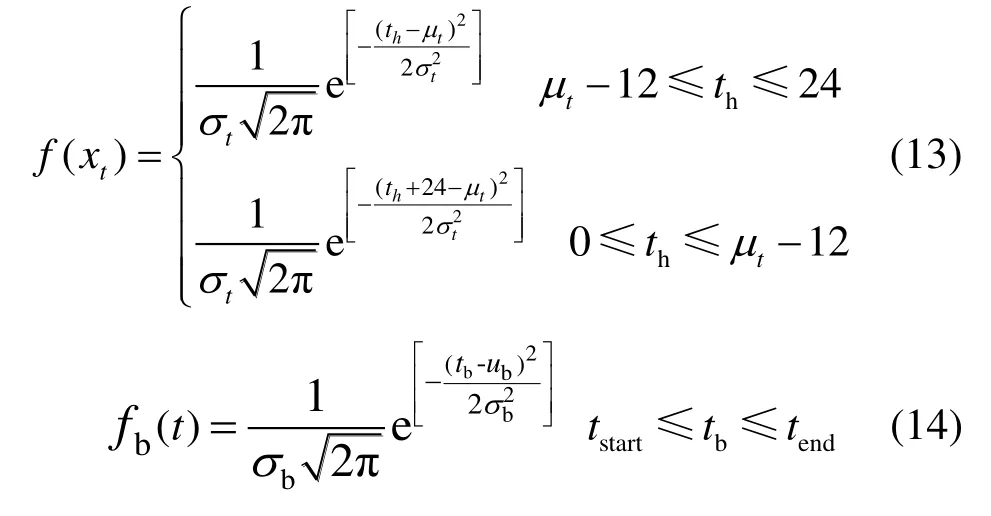
式(13)为返回住宅区时刻分布函数，式中：th为住宅区用户返程时间；μt为期望值，取17.6；σt为标准差，取3.4。式(14)为到达办公区时刻分布函数，式中：tb为办公区用户返程时间；μb为期望值，取11；μb为标准差，取3；tstart、tend分别为开始、结束时间，分别取4、20。

2.5 柴油发电机约束

柴油发电机模型包含功率约束和爬坡约束：

式中：PDG(t)为t时刻柴油发电机组出力；PDG,max、PDG,min分别为柴油机组出力上、下限；ΔPDG,max、ΔPDG,min分别为柴油机组出力上、下爬坡功率。

2.6 新能源出力约束

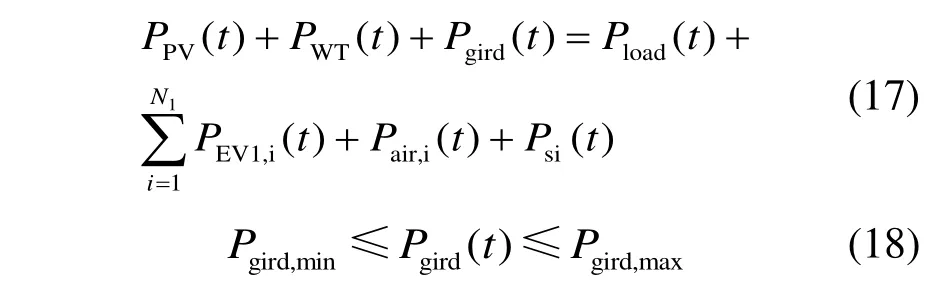
式中：PPV(t)、PWT(t)分别为光伏、风机t时出力，Pgrid,max、Pgird,min分别为与上级电网交互功率上、下限。

3 日前调度的分布式优化求解

3.1 优化问题分解

由于直接求解会给调度中心带来巨大的计算压力，基于同步型ADMM对问题进行分布式求解。求解得到的相邻区域耦合支路变量要相等，保证解决的是同一问题[9]。为此，建立控制模型：

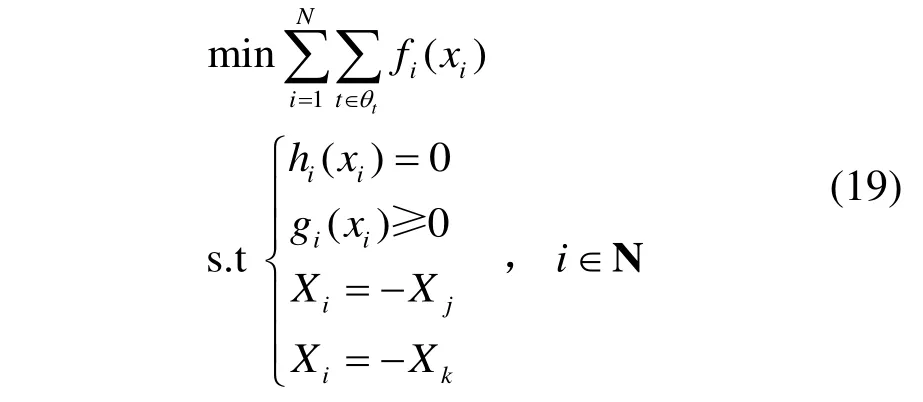
式中：fi(xi)表示区域i的目标子函数；hi(xi)表示区域i的功率等式约束；gi(xi)表示区域i设备的不等式约束；Xi表示系统i与相邻区域的耦合变量；j、k为i相邻的区域。

3.2 同步型ADMM分布式求解

ADMM收敛速度快、鲁棒性强，通过分解能使问题简单化，可以解决大规模优化问题，成为近年来较多使用的分布式求解方法[14]。由于所建立日前模型是目标函数可分、边界耦合约束线性的凸优化模型，故采用同步型ADMM对其求解较为适宜[9,15-16]。基于文献[9]所介绍分布式求解方法对各区域进行求解，其目标函数对应的拉格朗日函数分别：

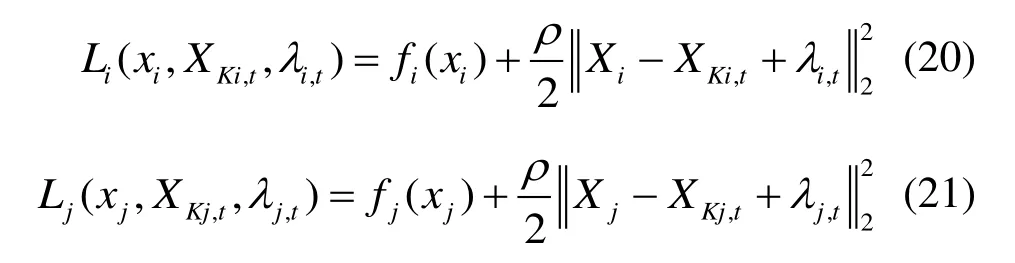
式中：t为迭代次数；ρ为ADMM的罚参数；λi和λj分别为区域i和j对偶变量组成的量。

设区域i与区域j、k相耦合，区域j与区域l、i相耦合，XKi,t和XKj,t分别为区域i和j第t+1次迭代的参考值，取区域i和j第t次迭代得到的相邻耦合支路状态的平均值：

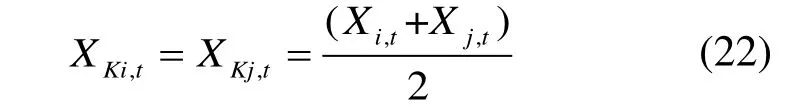
各区域的约束条件可参见式(2)—式(18)，各区域的控制器按如下具体步骤对优化问题进行分布式求解：

1）迭代t+1次，区域i与区域j内的各自求解自身目标，并行计算Li(xi,X Ki,t,λi,t)和Li(x j,X Kj,t,λj,t)，获得各区域耦合支路状态Xi,t+1和Xj,t+1：

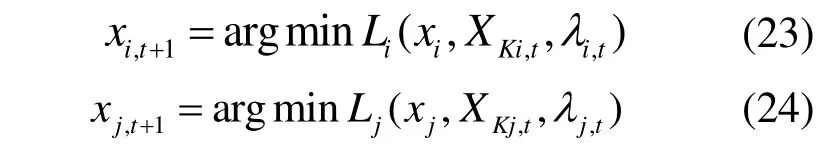
2）基于区域i与区域j耦合变量状态，计算耦合变量的平均值如式(22)，得XKi,t和XKj,t，并作为下一次迭代的参考值；

3）各区域内的对偶变量进行迭代更新：

4）判断算法是否收敛，当边界残差趋于零或迭代次数达到设定值或相邻区域耦合变量二范数的平方小于等于所设置残差时，即：

跳出迭代，算法结束。

4 日内优化模型

4.1 日内预测模型

日内考虑风、光以及负荷日前预测的不确定性，利用模型预测控制（model predictive control,MPC）修正日内实际运行计划与日前调度计划间的偏差[17]。以区域i、j、k两两相连构成闭合环网为例，选取与上级电网交互功率、区域i与区域j相邻联络线交互功率、区域j与区域k相邻联络线交互功率、光伏功率、负荷功率、聚合空调功率、电动汽车功率为状态变量，通过引入储能系统与响应快速的电动汽车系统与区域i与区域j、区域j与区域k相邻联络线交互相较日前变化功率作为控制变量，以光伏和负荷预测误差作为扰动输入，可建立日内预测模型：

4.2 日内目标函数

日内滚动优化的目标为修正日内实际运行值与日前调度值的偏差，同时使储能发挥日前削峰填谷作用；目标函数为：

式中：Pgrid,ref(t)为日前电网交互功率；PMGi_j,ref(t)、PMGj_k,ref(t)分别为区域i与区域j、区域j与区域k相邻联络线日前交互功率。

4.3 约束条件

4.3.1 功率平衡条件

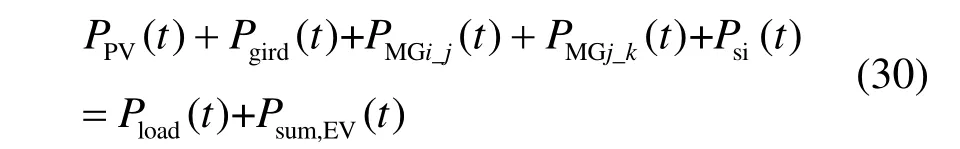
式中：PPV(t)、PWT(t)、Pload(t)分别为日内光伏、风机和负荷预测出力；Psum,EV(t)为空调聚合功率。

4.3.2 聚合电动汽车负荷约束

电动汽车负荷上下可调整量可表示为：

式中：ΔPsum,EV,min(t)、ΔPsum,EV,max(t)分别为聚合电动汽车可调整上下限。

4.3.3 相邻电网联络线交互功率约束

为促进日内区域间的电能互补互济，引入如下区域间联络线交互约束：

式中：DPMGi_j(k)、DPMG,j_k(k)分别为区域i与区域j、区域j与区域k相邻联络线交互功率较日前调整量。

4.3.4 储能系统约束

日内因储能具有响应速度快的优势，为更好地消纳剩余新能源，平抑波动，日内增加储能系统约束；其约束条件可见式(2)—式(4)。

5 算例分析

基于MATLAB2016b软件中YALMIP平台进行算法实现，采用CPLEX工具包进行相应求解，所采用电脑为i7处理器，主频为2.2 Ghz，选取含3个区域的有源配电网为研究对象，其电网拓扑结构如图3所示。考虑到各区域间距离相差不大，故各区域内的光照强度和风速基本相同，其中区域MG1光伏装机容量1 500 kW，风机装机容量2 500 kW，储能容量750 kW·h，柴油发电机装机容量500 kW；区域MG2光伏装机容量1 300 kW；区域MG3风机装机容量1 200 kW；区域间互济互补主要受不同区域负荷特性差异影响；所考虑区域间联络线交互功率上限为300 kW。

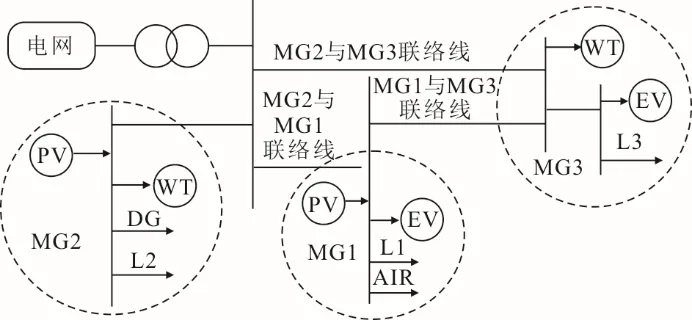
图3 有源配电网拓扑结构Fig.3 Active distribution network topology

各区域内用能设备模型采用本文第2节日前优化模型，各区域内所包含具体设备见表1；考虑相邻区距离较近，故各区域与上级电网交互电价均按表2各时段电价所示；区域内各新能源发电量如图4所示；选取典型工业以及办公居民负荷曲线作为本算例各区域负荷设定值，具体如图5所示。

表1 各区域系统资源配置Tab.1 Regional system resource configuration

表2 区域各时段电价Tab.2 Electricity price of each period in the region

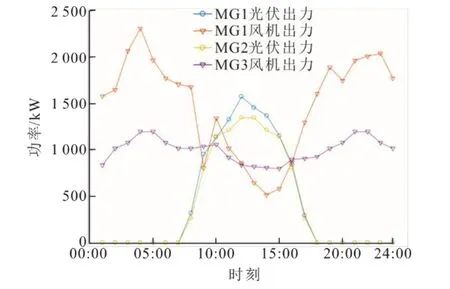
图4 各区域内新能源发电量Fig.4 New energy power generation in each region

图5 各区域负荷设定值Fig.5 Load setting values for each region

基于本文所介绍同步型ADMM对所建立日前模型进行分布式求解，求解时间间隔为1 h。设置惩罚因子ρ为0.05，收敛参数δ为1e-3，迭代次数上限为50次，各区域迭代收敛残差如图6所示。由图6可见：各区域残差均处于明显收敛过程；在10次左右求解达到稳定，20次时残差收敛出现细小波动，后趋于稳定，可见相邻耦合区域变量无限接近，从而验证了日前优化目标分解的有效性。即采用分布式所求得结果与集中式无异，从而大大降低了计算压力。

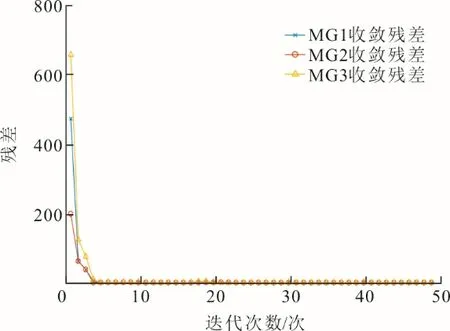
图6 迭代收敛残差Fig.6 Iterative convergence residuals

图7为相邻区域联络线交互功率。由图7可见，相邻区域通过联络线交互各系统内过新能源，以实现系统第1阶段能源消纳。当区域内新能源发电量不足以支撑负荷时，新能源出力过剩区域会将电能由相邻电网联络线输送至亏电区域。

图7 各区域联络线交互功率Fig.7 Interactive power of each regional contact line

由图7可见：05:00—06:00时段内，MG2区域因光伏出力较低不足以维持自身负荷，而MG3区域风机在此时段出力较高负荷较小，故将多余电量沿电网联络线传输至MG2区域，MG1区域也同样将电量经联络线传输至MG2区域；在12:00—13:00时段内，MG3区域新能源出力不足以维持自身负荷，此时MG2区域通过相邻电网联络线输电给MG3区域；在17:00—20:00时段内，MG1区域新能源出力过剩，多余电能将通过相邻区域联络线传输至MG2、MG3区域。其余时段的联络线能量传输同样与电网电价也紧密相关，当上级电网电价较低时会减缓相邻区域间的电能传输，以保证系统的经济性，当电价较高时则促进区域间的能量传输。

各区域日前调度各设备出力如图8—图10所示。由图8—图10可见：MG1区域中储能系统在新能源发电量大于负荷时进行充电，见图8中14:00—16:00、18:00—19:00时段；在新能源发电量小于负荷值时进行放电，同时接受相邻区域输送功率，当不足以维持自身功率平衡时，向电网购电。

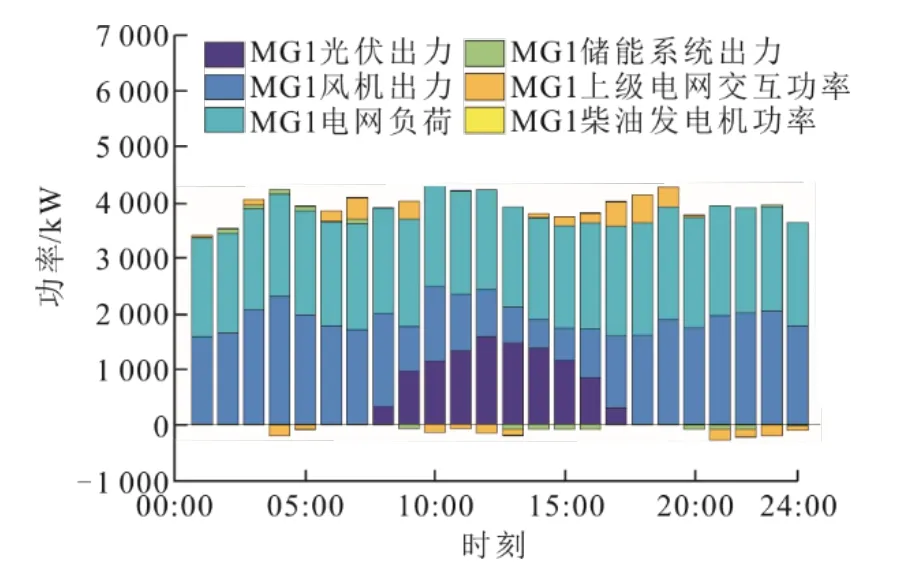
图8 MG1日前调度各设备出力Fig.8 MG1 day-ahead scheduling results

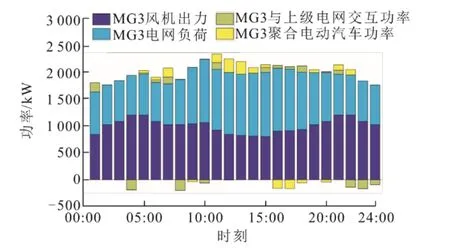
图10 MG3日前调度各设备出力Fig.10 MG3 day-ahead scheduling results

在夜间时段，各区域负荷需求量较少，区域选择向电网售电以维持自身经济性。MG2区域为住宅区，区域中电动汽车依据上文介绍蒙特卡罗算法对住宅区行驶规律函数进行抽样，聚合后电动汽车可调度时段集中在凌晨01:00—09:00、14:00—24:00，此时电动汽车参与能源消纳策略。在新能源发电充足时段进行充电，在新能源发电不足时段进行放电。在新能源发电充足时段增大功率进行虚拟储能，住宅区内空调作为虚拟储能设备，01:00—05:00时段空调制冷将温度维持在虚拟储能温度设定值下限，进行虚拟储能；在18:00—20:00时段，新能源发电量较少，不足以维持负荷需求，此时电动汽车放电，空调将温度维持在调节带宽上限进行虚拟储能放电。

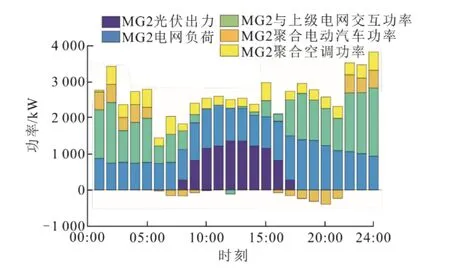
图9 MG2日前调度各设备出力Fig.9 MG2 day-ahead scheduling results

MG3区域中办公区电动汽车可调度时段集中在09:00—22:00，其规律均满足前文所述，在新能源发电量较大时，集群电动汽车进行充电，如图10所示在11:00—13:00时段电动汽车进行充电；在16:00—17:00时段内新能源出力低于负荷值，此时电动汽车参与放电以维持系统功率平衡。

至此第1阶段新能源消纳策略完成，第2阶段新能源消纳策略为日内能源消纳策略，以住宅区域MG2为例进行说明。通过在日前负荷基础上叠加随机扰动以模拟日内可在生能源及负荷出力，图11为日前日内新能源出力对比曲线。基于所建立式(28)预测模型进行滚动优化求解，求得电网日前日内与上级电网联络线对比曲线（图12）与日内各控制变量响应柱状图（图13）。

图11 日前日内新能源出力对比曲线Fig.11 Comparison of new energy output curves

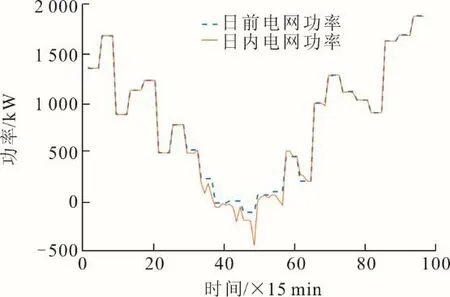
图12 电网联络线日前日内对比曲线Fig.12 Intraday comparison curve of the grid connection line

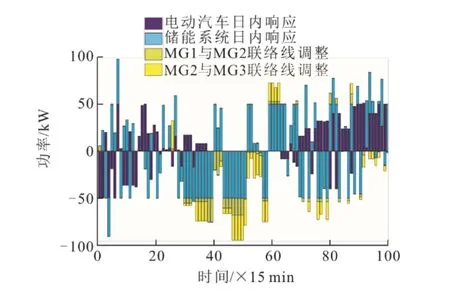
图13 日内控制变量响应柱状图Fig.13 Intraday control variable response histogram

由图12、图13可见，大部分时段日内电网联络线功率均紧紧跟踪日内调度时段，此时电动汽车、储能系统、MG1与MG2区域联络线功率、MG2与MG3区域联络线功率所组成的状态变量，通过调整以跟踪日前调度计划，从而实现日内新能源的消纳。电动汽车多在下午或夜间进行日内响应，这是由住宅区电动汽车行驶规律特性所决定。在27—50时间段处，光伏发电增大，电动汽车、储能等进行充电调整，多余电能通过电网联络线向相邻电网进行输送，但仍未能消纳剩余光伏，此时与上级电网联络线出现偏差，以增加向电网售电，维持此时功率平衡。

6 结 论

1）为提高区域内新能源消纳量，本文提出一种计及电动汽车的有源配电网两阶段分布式新能源消纳策略，在前阶段建立以新能源消纳量最大化即与大电网交互最少同时兼顾自身利益的优化模型；日内阶段引入储能电池通过对各控制变量的调节以实现第2阶段新能源消纳。

2）第1阶段日前新能源消纳模型考虑电动汽车作为可调度资源，结合不同区域出行规律特性，对其内部电气设备进行协调调度；各区域间考虑相邻区域联络线功率交互以实现区域间的互补互济，以最大限度消纳区域新能源提高系统稳定性。

3）将集中优化问题进行分解求解，从而将复杂问题进行分布式求解，大大降低了计算量，以含3区域有源配电网为例，所求得相邻区域迭代误差无限接近0，从而验证分布式求解的可行性。

4）第2阶段考虑日前源荷预测的偏差，通过引入储能系统并结合电动汽车快速响应的特性，通过对电动汽车与储能系统的协调调度，以跟踪日前各区域间联络线传输功率，从而实现第2阶段新能源消纳，并跟踪日前调度计划