子母弹反机场跑道封锁概率快速计算方法*

刘云辉，冯 源，高月光，冯顺山

（1.北京理工大学爆炸科学与技术国家重点实验室，北京 100081；2.中国兵器科学研究院，北京 100089）

0 引言

机场跑道作为现代战争中夺取制空权的关键，其作用日益彰显。近几年的多次局部战争表明，若能在战争中对敌方机场跑道进行有效封锁，则可在后续作战中掌握主动权。而若能及时并准确评估对机场跑道的封锁程度，分析弹药对其的封锁概率，对掌控战场态势、制定后续作战方案具有显著的军事意义。

在子母弹对机场跑道封锁概率计算模型方面，国内已有大量学者对此开展了研究，现有的模型通常采用蒙特卡洛法，通过像素仿真法、空间遍历法、区域搜索法或随机抽样法等方法对最小升降窗口进行搜索，进而计算出子母弹对机场跑道的封锁概率。像素仿真法、空间遍历法原理简单，但其计算准度受到所取的像素点大小、遍历步长的限制，要求取具有一定准度、精度的结果，需要大量的时间与计算机资源。区域搜索法基于子弹药落点搜索最小起降窗口，其计算准度与评估速度相比像素仿真法、空间遍历法得到了大幅提高，但是其只能搜索平行于跑道的直起降窗口，对于斜起降窗口则力有未逮，评估结果相比实际值偏大。随机抽样法基于蒙特卡洛法原理，在跑道上随机抽取大数量的矩形来判定是否有完整的最小起降窗口，可有效应对斜起降状况，在取样次数达到一定数量的前提下，相比之前的方法，可大大提高结果准确度，但是，蒙特卡洛法的复用，使得基于随机抽样法建立的封锁概率计算模型的计算时间大大增加。

综上，基于蒙特卡洛方法的封锁概率计算模型准确度已逐步提高，并可考虑到斜起降窗口的情况，但是这些计算模型一直未脱离蒙特卡洛法的制约，求取精度与评估耗时的矛盾性一直存在，其达到秒级、分级的评估时间，已无法适应时代的发展。随着毁伤效果侦察评估弹药的提出与研制，研究更快速的封锁概率计算方法已成为无法回避甚至必须解决的问题。

考虑到神经网络具有可以逼近任何非线性映射关系的能力。在效能评估领域，已有众多使用案例。如在鱼雷作战效能、潜射反舰导弹作战效能、电子战效能评估、炮光集成武器系统作战效能等方面已有应用；在基于传统蒙特卡洛方法计算模型的基础上，采用神经网络算法对封锁概率计算模型进行拟合，在此基础上可实现概率的快速计算，使得评估时长缩短至毫秒级，同时也可兼顾蒙特卡洛方法结果的优点。

1 子母弹反机场跑道封锁概率计算模型

1.1 子弹药落点散布计算模型

以机场正中心为坐标原点建立坐标系，机场跑道长宽分别为L、B。假设共对机场发射N 枚母弹，第i 枚母弹预定抛撒坐标地面投影为（x，y），在应对一条机场跑道的情况下，追求最大封锁概率，母弹预定瞄准坐标一般会设定为机场跑道中轴线，即y=0。母弹实际抛撒坐标（x'，y'）（i=1，2，3，…，N）为：

式中，CEP 为子母弹平台圆概率偏差；r、r为服从标准正态分布N（0，1）生成的随机数。

在上述基础上，假设每枚母弹装填n 枚子弹药，考虑子母弹抛撒半径R 及抛撒中心盲区半径R，则第i 枚母弹的第j（j=1，2，3，…，n）枚子弹药的落点坐标（x，y）为：

式中，t为服从均匀分布U（R，R）生成的随机数；t为服从均匀分布U（0，2π）生成的随机数。

1.2 子母弹对跑道封锁概率计算模型

基于蒙特卡洛法，在随机生成的子弹药落点基础上，考虑子弹药的毁伤半径R，在子母弹的打击下，机场跑道是否存在可供飞机起降的最小起降窗口。若机场存在完好的最小起降窗口，则说明此次仿真计算中封锁失败；若机场在子母弹打击下不存在完好的最小起降窗口，则说明此次仿真中封锁成功。

假设在仿真中共进行M 次蒙特卡洛计算，其中有M次计算中跑道被完全封锁，则子母弹对机场跑道的封锁概率P为：

在子母弹抛撒参数，CEP 性能、机场尺寸、起降窗口尺寸等参数不变的情况下，封锁概率可视为母弹预定抛撒坐标的函数，即：

式中，x为第i 枚母弹的预定抛撒横坐标；f 表示封锁概率非线性函数。

2 基于神经网络的算法研究

2.1 BP 神经网络理论

BP（back propagation）神经网络是一种基于误差反向传播算法的神经网络，由一层输入层、一层或多层隐藏层和一层输出层组成的多层网络结构。如图1 所示为其基本结构。由于BP 神经网络具有可以拟合任意非线性映射关系的能力，因此，可以用来对子母弹反机场跑道封锁概率与子母战斗部预定瞄准坐标之间的非线性关系进行非线性拟合。

图1 BP 神经网络结构

网络中每个神经元以上一层的所有神经元的输出作为输入，相应的输出为：

式中，h（j）为第i 层第j 个神经元的输出，以输入层为第1 层，输出层为最后一层；b（j）为该神经元的偏置系数，N表示上一层神经元的数量；w（j，k）则表示该神经元的权重系数；g 为神经元的激活函数，取S 型函数，即：

在网络进行训练学习时，根据网络输出的预测值P与输入样本值P 的误差，来不断调整每一个神经元中的权重系数和偏差系数。由于只有一个输出，故误差计算公式为：

每次学习后，权重系数w 以及偏差系数b 的调整为：

式中，η 为学习率，一般取0.01～0.5。

经过多次迭代学习训练，反复调整权重系数以及偏差系数，使得整体误差渐次降低，直至达到预定误差ε，即可获得对目标非线性函数有较好拟合性能的神经网络模型。

2.2 算法思想

整个算法分为两部分：

1）随机生成一定数量的（x，x，…，x）（x～U（-L/2，L/2），i=1，2，…，N），输入到子母弹对机场跑道封锁概率计算模型模拟N 枚母弹打击机场跑道，对其封锁概率进行评估计算，形成初始数据集。

2）将形成的数据集输入到神经网络中，在构建合适的神经网络结构中进行迭代优化计算，获得最优权重系数以及偏差系数，以获得对封锁概率非线性函数具有较好拟合性能的神经网络模型。

图2 子母弹反机场跑道神经网络封锁概率计算模型训练示意图

3 案例计算与结果分析

3.1 计算条件

1）计 算 机 实 验 环 境：Intel （R）Core（TM）i5-8250U CPU @ 1.80 GHz，内存为8 GB，Window10操作系统，Matlab R2015a 版本；

2）机场跑道：长L=2 400 m、宽B=60 m；

3）飞机最小起降窗口：长L=800 m、宽B=20 m；

4）最小起降窗口搜索方法：随机抽样法，抽样次数为10 000 次；

5）子母战斗部参数：子弹药数量n=150 枚，抛撒半径R=120 m，抛撒中心盲区半径R=15 m，子弹药毁伤半径R=1 m，CEP=100 m；

6）蒙特卡洛模拟仿真计算次数：M=10 000 次；

7）子母弹数量N：2 枚；

8）数据集数量：20 000 组；

9）预定误差ε：1×10。

3.2 计算结果与分析

任选数组母弹瞄准坐标（x，x），分别使用空间遍历法、区域搜索法、随机抽样法以及神经网络法，在相同的计算机软硬件条件下对封锁概率进行计算，并计算了神经网络法对比随机抽样法的相对误差。其中，空间遍历法各方向的遍历步长参数的选取决定计算结果准度与计算耗时，步长越小，则结果越准确，但相应的计算耗时会成倍地增加，为使结果具有一定的准度并保证计算耗时在可接受范围内，经过计算分析后选取遍历步长为0.25 m。随机抽样法抽样次数为10 000 次，其各方法封锁概率计算结果如表1 所示，相对误差为神经网络法结果与随机抽样法结果的相对误差。

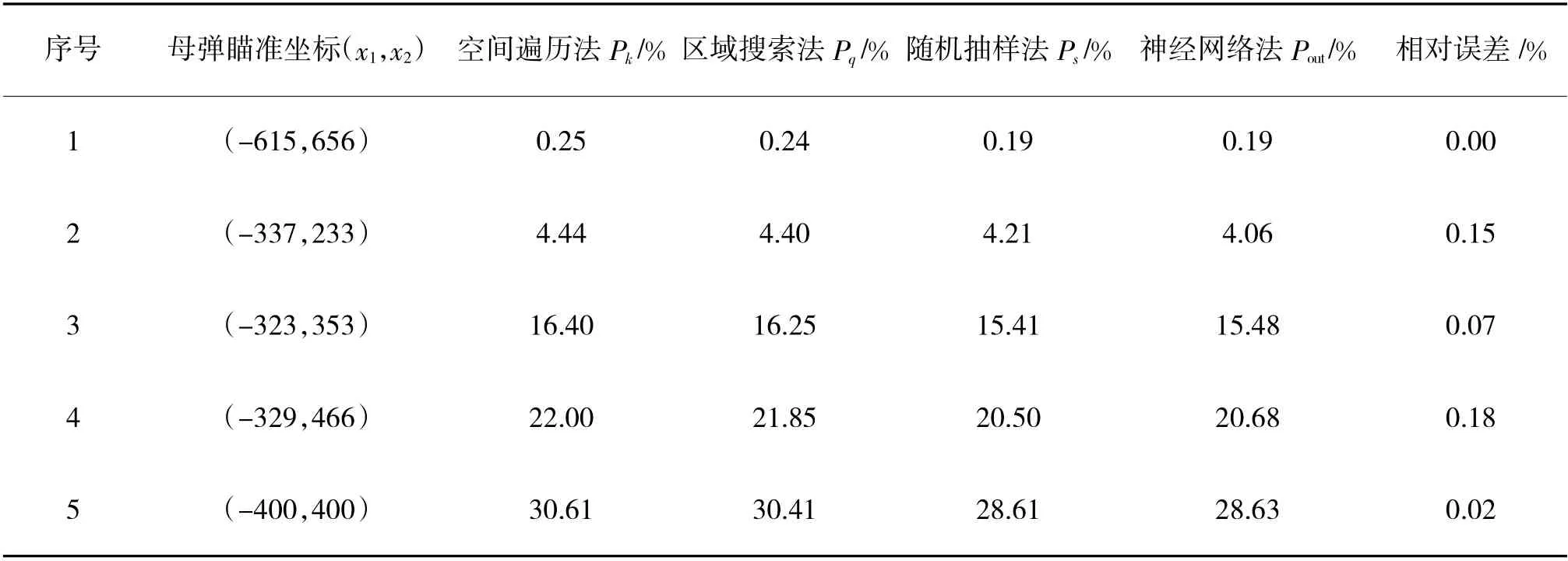
表1 仿真计算结果精准度分析

空间遍历法由于遍历步长的选取，相比区域搜索法会存在一定的漏判，其结果相对区域搜索法应偏大，而区域搜索法由于无法搜索斜跑道，致使其结果相对随机抽样法结果偏大，随机抽样法所得封锁概率结果具有最高的准确度。分析表中数据可发现，其结果与上述理论分析一致。由于神经网络学习对象为基于随机抽样法的蒙特卡洛模型，其计算结果与随机抽样法结果最大相对误差为0.18%。结果相对随机抽样法结果的精度符合工程应用要求。各方法封锁概率计算所需时间结果如表2 所示。

表2 仿真计算耗时结果分析

空间遍历法计算所需时间达到小时级，区域搜索法基于子弹药落点的跑道搜索原理，大大提高了计算所需时间，但也达到了秒级，计算结果相对快速，但由于无法考虑斜起降情况而使得结果准确性有待提高，随机抽样法计算结果具有最高的准确性，但是其计算所需时间达到分级、小时级，并且封锁概率越大，所需时间越长。神经网络法在继承随机抽样法准确度的情况下，其评估耗时大大缩短，达到了毫秒级，大大缩短了评估耗时。

4 结论

针对传统基于蒙特卡洛法的毁伤效果侦察评估弹对子母弹反机场跑道封锁概率模型计算速度慢，无法实现战场实时评估问题，提出使用神经网络对传统蒙特卡洛模型进行学习和拟合，建立了基于神经网络的子母弹反机场跑道封锁概率计算模型，并对2 枚母弹条件下的封锁概率进行了仿真计算，仿真结果表明：该方法能较好地拟合基于蒙特卡洛方法的子母弹反机场跑道封锁概率计算模型，学习训练好的神经网络模型能够比较准确地给出反机场跑道封锁概率结果，计算精度可满足工程应用要求，同时评估时间相比于传统蒙特卡洛法得到了大大缩短，从秒级缩短至毫秒级，实现战场毁伤效能实时计算要求，具备实用性和通用性。本方法可为各类毁伤效果侦察弹对机场跑道封锁效能实时评估计算提供可行方法。