基于量子粒子群优化的无人机攻防博弈决策*

刘佳敏，吴庆宪，王玉惠，周大可

（南京航空航天大学自动化学院，南京 211106）

0 引言

无人机在空战中需要根据复杂的战场信息决策出最优的战术方案。常用的攻防决策方法有专家系统法、狼群算法和影响图法等，但这些方法有一定的局限性，如专家系统法的可适应性较差。而采取以博弈论为基础的决策方法更能体现空战的对抗性，如文献［7］提出了一种矩阵对策法与遗传算法相结合的空战决策算法等。然而由于传感器精度、战场环境干扰等原因，采集的空战信息具有不确定性，这会影响空战攻防决策的正确性。

关于不确定信息下无人机空战攻防博弈的研究，目前已有文献报道，并取得了一些研究成果。文献［10］建立了无人机空战机动直觉模糊博弈模型，但模糊数属性权重的确定具有主观性。文献［11-13］基于区间数对不确定环境无人机攻防博弈策略进行了研究，但是没有充分考虑战场态势对攻防博弈的影响，并且没有客观确定态势权重。根据以上文献的研究成果可以分析出，学者们已开展不确定信息下无人机空战攻防博弈问题的研究，但还需充分考虑战场态势，以及客观确定态势权重。

综上分析，针对无人机空战面临信息不确定等挑战，本文基于区间数和量子粒子群优化（quantum particle swarm optimization，QPSO）提出一种无人机空战攻防博弈模型。该模型采用区间数表示不确定信息，然后态势分析，借助集对分析和QPSO 算法确定态势最优权重，建立博弈支付函数，获得区间数支付矩阵。结合区间数可能度概念，采用QPSO 算法对双方混合策略纳什均衡和期望收益区间进行求解。最后通过仿真，验证该攻防博弈模型解决不确定环境下无人机攻防博弈问题的有效性。

1 不确定信息下无人机攻防博弈决策问题

1.1 空战问题描述

不确定信息下无人机空战攻防博弈决策原理如图1 所示。无人机攻防博弈问题需要根据双方无人机的角度、距离、速度、高度和性能数据计算态势，并对态势权重进行寻优，从而计算区间数支付矩阵进行决策。

1.2 确定最优指标权重

1.3 区间数支付矩阵建立

2 不确定信息下基于区间数的攻防博弈决策

建立攻防博弈模型，结合区间数的可能度公式，采用QPSO 算法来求解纳什均衡策略。

2.1 不确定信息下基于区间数的攻防博弈模型

对单矩阵博弈问题的求解本质上是对式（14）进行求解，结合区间数的可能度概念，采用QPSO 算法求解纳什均衡。

2.2 攻防博弈决策流程

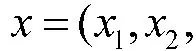
攻防博弈决策的具体步骤如下：

Step 1 采集不确定空战信息，用区间数表示；Step 2 分析双方每架无人机态势，根据优势函数计算态势区间数矩阵，并转化为联系数矩阵；

另外，围绕硕博士学位论文的使用价值，机械与动力工程等学科提出学位论文有助于读者快速了解某一领域发展及研究现状，是学科用户从事科研活动必不可少的一类文献来源。

Step 3 根据得到的态势联系数矩阵和式（2）～式（8），采用QPSO 算法寻找每架无人机的最优权重；

Step 4 根据Step 3 得到的最优权重和式（9）～式（12），计算博弈区间数支付矩阵，并根据式（13）、式（14）将单矩阵博弈问题转化为线性规划问题；

Step 5 采用QPSO 算法求解敌我双方的混合策略纳什均衡。定义无人机策略粒子种群和适应度函数，结合区间数的可能度，根据式（15）～式（18）迭代更新个体最优策略粒子和全局最优策略粒子；

Step 6 重复Step 5，直至达到最大迭代次数，输出全局最优策略粒子，即敌我方无人机混合策略的纳什均衡解。

由于支付矩阵为区间数矩阵，策略粒子的适应度值也为区间数，通过可能度来比较适应度值。设定策略粒子的适应度值为

3 无人机攻防博弈决策仿真

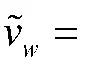
表1 敌我双方策略集（部分）

我方和敌方无人机空战信息（角度、速度、高度、距离）如下页表2、表3 所示。

表2 我方UAV 角度、速度态势、UAV 高度、距离态势

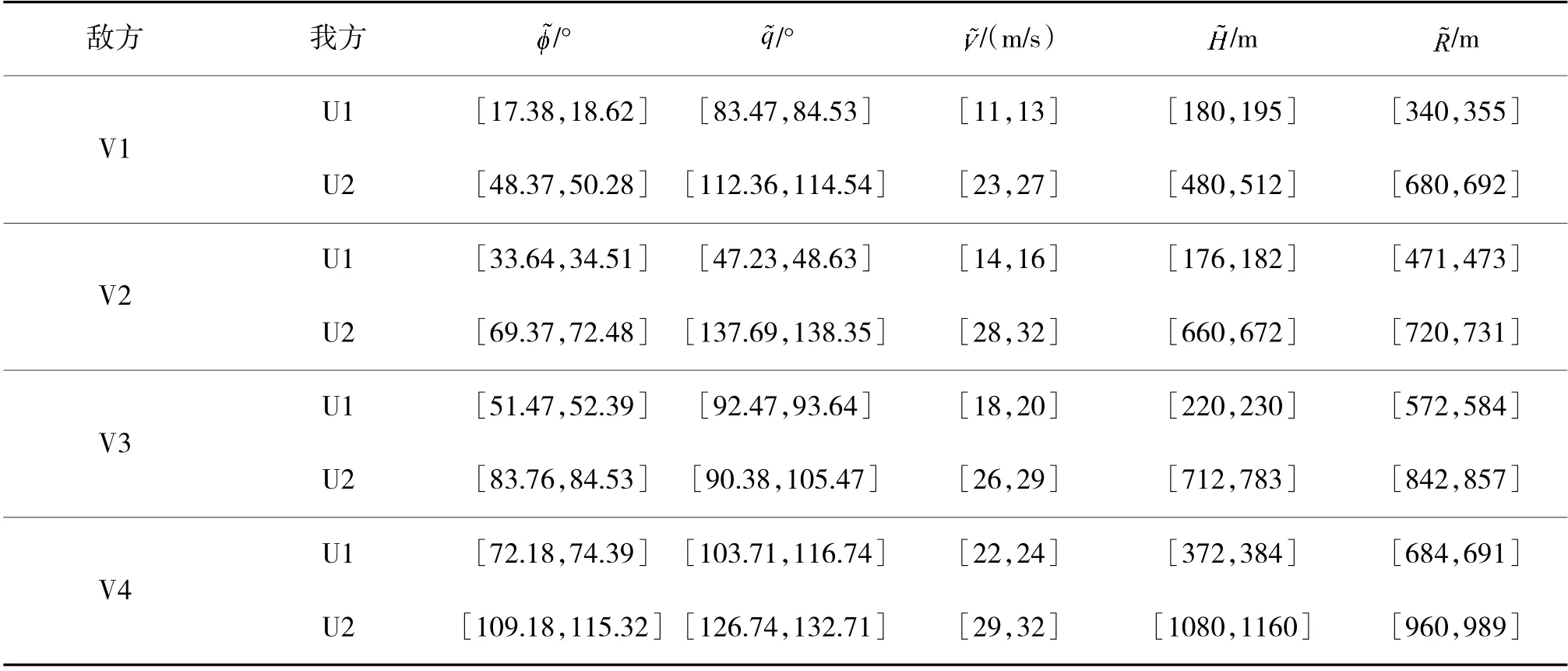
表3 敌方UAV 角度、距离态势、UAV 高度、距离态势

表4 我方对敌方最优态势权重

表5 敌方对我方最优态势权重

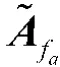
当我方选择策略x，敌方分别选择策略y、y、y、y、y、y、y、y、y、y、y、y、y、y、y、y时，我方区间支付值分别为［-2.334 3，-1.902 2］、［-2.233 2，-1.866 2］、［-2.490 0，-1.973 1］、［-2.388 9，-1.937 0］、［-2.580 5，-2.060 8］、［-2.479 4，-2.024 7］、［-2.736 2，-2.131 6］、［-2.635 1，-2.095 5］、［-2.450 8，-2.006 9］、［-2.349 7，-1.970 9］、［-2.606 5，-2.077 7］、［-2.505 4，-2.041 7］、［-2.697 0，-2.165 5］、［-2.595 9，-2.129 4］、［-2.852 7，-2.236 3］、［-2.751 6，-2.200 2］。

图2、图3 为QPSO 算法求解纳什均衡过程中敌我方适应度变化曲线。分析可知，经过一定次数迭代后，QPSO 算法能找到各自无人机的全局最优粒子，即敌我方混合策略纳什均衡，验证了区间数攻防博弈模型解决不确定环境下无人机攻防博弈问题的有效性。

图2 我方的区间适应度变化曲线

图3 敌方的区间适应度变化曲线

对比QPSO 算法和PSO 算法求解混合策略纳什均衡解的性能。分别用这两种算法进行多次迭代求解实验，并计算各自求得全局最优解的平均迭代次数，结果如表6 所示。

表6 两种算法的平均迭代次数

通过表格数据可得，QPSO 算法求解区间数支付矩阵混合策略纳什均衡解的平均迭代次数更少，体现QPSO 算法的性能优越性。

4 结论

针对不确定环境下空战，本文提出一种无人机空战攻防博弈模型。该模型中不确定空战信息用区间数表示，借助集对分析理论处理区间态势，用QPSO 算法对态势权重进行寻优，完善博弈支付函数；结合可能度概念，采用QPSO 算法求解敌我方攻防博弈的混合策略纳什均衡，并比较QPSO 算法和PSO 算法求得全局最优解的平均迭代次数。该模型还可以应用于其他不确定信息的博弈问题研究，但也还存在不足之处，在之后的研究中会不断完善改进。