基于全变分的烟雾浓度检测方法*
安明伟,钱丽英,李洪昌
(南京信息职业技术学院网络与通信学院,南京 210023)
0 引言
烟雾浓度是对烟雾量大小及其烟雾危害程度的度量,也是了解大气的稳定度和垂直结构的天气指标。在交通运输安全、火灾初期烟雾检测和军事领域,烟雾浓度定量测量有着重要意义,是一个极为重要的因素。在军事领域,烟雾给飞机起降、舰艇编队航行、军地联合作战和火力指挥与运用等带来困难。传统烟雾度仪器检测法受取样空间限制,难以反映环境真实状况,同时价格昂贵,灵活性差,不宜普及。当前,视频传感平台广泛应用,基于视频传感系统,构建起先进的烟雾浓度监视系统,提高了环境烟雾检测的“透明度”。基于视频分析的检测法,具有易操作等优点,已成为研究热点。
1 烟雾浓度检测方法分析
基于图像的烟雾检测方法,其核心是如何表征烟雾的自身特征。烟雾的特征主要有静态特征和动态特征,静态特征通常包括图像的颜色变化,比如背景模糊特征;动态特征通常包括烟雾的扩散性、不规则性、运动方向性等。通过烟雾的自身特征为基础的分析,利用图像的分形特征、灰度信息、模糊度、小波能量等要素,可准确有效地识别烟雾,并能够实现对烟雾浓度的检测。
2013 年,袁飞阁提出基于图像灰度特性检测烟雾浓度的方法,在火灾检测中,火灾检测的精度与抗干扰能力得到提升,但是该方法只能实现浅白色烟雾浓度的检测,在测量时,对背景图像的灰度特征有一定的依赖性,并且对于黑烟检测效果不理想。2014 年,MIAO L G 改进了烟雾检测,通过暗通道法实现视频烟雾检测,把烟雾浓度粗略近似为暗通道的强度。2017 年,马天颖给出了通过图像结构相似度计算烟雾浓度的方法,把转换系数用图像复杂度的负值来代替,该方法实现了基于图像结构相似度的不同背景图像条件下烟雾浓度的定量测量,在定性检测到烟雾存在的同时,能较准确地测量出烟雾浓度值。2018 年,CHENG X G 提出了一种变分框架来处理消光系数的时变性质,并通过对观测到的亮度曲线进行分段函数拟合,提取消光系数,实现雾霾天气下的实时大气能见度估计。
不过,烟雾与噪声具有一定的相似性,图像中烟雾的存在同样会使背景图像变得模糊,造成图像质量下降,且烟雾浓度越大,图像质量下降的程度越大。以上烟雾检测方法,有的是通过检测烟雾的动态特征或静态特征实现的,会导致在区分与烟雾特征相似的物体时能力较弱,在区分与烟雾特征相似的物体时有一定的局限性;有的只是实现烟雾图像的能见度检测,未定量计算烟雾浓度。
2 烟雾浓度的定义
由于不同条件下产生的烟雾量有所不同,依据不同的衡量方法会对结果产生一定的影响。因此,目前对于烟雾浓度的定义标准尚没有统一。本文针对雾霾等烟雾,选用消光系数来定义烟雾浓度这一主流方法,下文所提烟雾浓度统指消光系数。
消光系数是烟雾浓度检测的一个重要参数,消光系数是指被测介质对光的吸收大小值,分为吸收系数和散射系数。比尔朗伯定律指出,在混沌介质或吸收介质中传播时,光能量将不断衰减。对于平面波而言,在线性范围内,所消耗的能量与光通行的距离成正比。如式(1)所示:
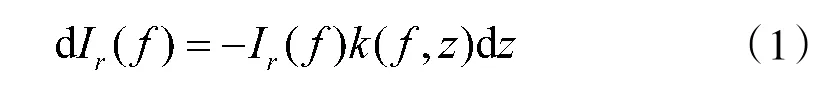
式中,f 表示光波频率;dz 是微分距离;I(f)表示入射到dz 所在面的通量密度;k(f,z)是与烟雾浓度密切相关的消光系数,也称为摩尔消光系数,它是f 和z的函数。
Koschmieder 于1924 年在上述原理的基础上,总结了布格- 兰伯特(Bougner-Lamber)定律,推导出消光系数与目标物亮度的关系公式,奠定了烟雾浓度检测的理论基础。即式(2)所示:
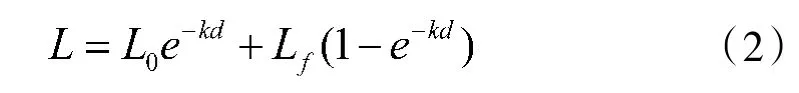
式中,L 为观测点观测到的目标物亮度;L表示目标物自有亮度;L代表背景天空亮度;k 是消光系数;d为观测点到目标物距离,对于环境而言,表示监控摄像机到目标物的距离。
Duntley 于1949 年在Koschmieder 定律基础上,推导出大气衰减定律,如式(3)所示:

式中,C 表示目标物视亮度对比度;C为目标物固有亮度对比度。令ε 为式(4):

ε 称之为视觉对比阈值,国际民航组织(international civil aviation orgainzation,ICAO)推荐ε=0.05,则可以得到大气烟雾浓度如式(5)所示:
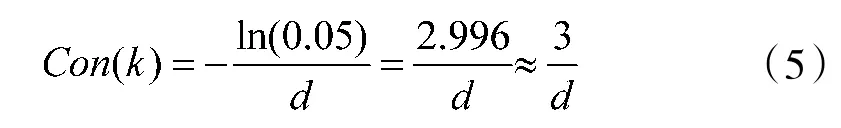
式(5)即为烟雾浓度检测的基本公式。
3 全变分的烟雾浓度检测算法
在文献[4-8]中,成孝刚、安明伟等研究了全变分的数字图像自相关函数的优化逼近模型、图像质量评估方法、全变分与图像清晰度之间的关系、变分框架来处理消光系数的时变性质等,提出了当图像因为各种原因变得模糊时,图像的低频成分增大,图像边界之间的差异变小,其全变分(total bounded variation,TBV)值逐渐下降。正常天气监控图像为比较清晰,主体为高频信号,边界差异较大。有烟雾后,图像变得模糊,相当于在清晰图像上出现大量噪声,烟雾越浓等同于噪声越多,烟雾浓度也越低。验证数据显示,烟雾浓度越来越高时,监控图像的全变分值越来越小。本文在图像变得模糊时其全变分值也会相应降低的性质基础上,在烟雾浓度检测中,基于Koschmieder 理论,构建泛函,并对其求变分,以分段平稳分析的思想对目标函数求极值,从而求出消光系数,进而得到当前烟雾浓度,提出了基于全变分的烟雾浓度检测方法。
3.1 全变分与烟雾浓度关系
跳跃部分和平滑波动两部分组成数字图像,与之相对应,含有烟雾的视频图像,其纹理边界的差异变小,跳跃部分变得相对平滑,可以视为模糊图像来处理。基于全变分的特征性质,全变分可以有效将图像边界之间的差异性表征出来。烟雾浓度升高对应的图像模糊度升高,反映此烟雾信息的视频图像变分会下降。在全变分理论的基础上,构建全变分与图像模糊度之间的关系模型,用以准确度量烟雾浓度与全变分之间的关系,进而极值状态的全变分值可作为烟雾浓度评估的准则。
根据全变分定义,设f 表示清晰图像,函数f(x,y)表示图像中第(x,y)像素。当烟雾清晰图像变得模糊,设模糊图像的像素为函数g(x,y),忽略噪声影响,函数g(x,y)=h(x,y)*f(x,y),h(x,y)为退化函数。根据文献[4-10],任意M×N 数字图像z 的全变分TBV 离散型是为
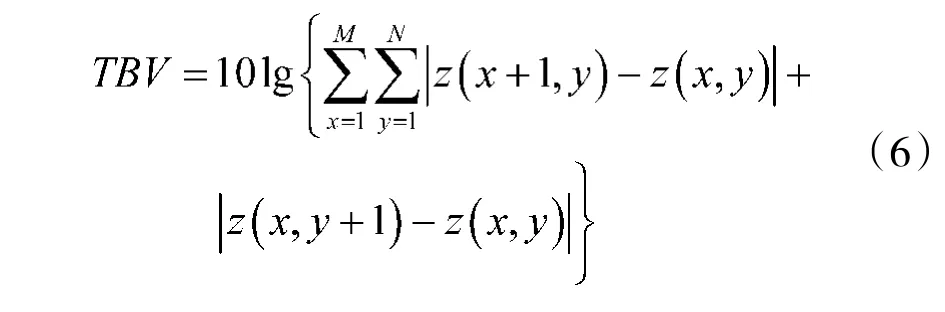
在此基础上,可分别计算出清晰图像f 的全变分TBV和模糊图像g 的全变分TBV,分别由式(7)、式(8)求解。

式(7)、式(8)中Ω 表述如式(9)所示:
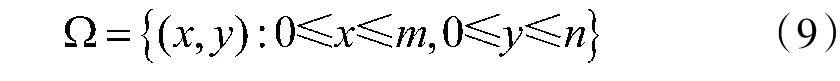
m,n 为原始清晰图像的尺寸大小。
烟雾浓度和总有界之间的关系如图1 所示。图中虚线为全变分值,其曲线为随着烟雾浓度减小的变化趋势,实线为烟雾浓度,代表着模糊程度,其曲线为随着烟雾浓度减小的变化趋势。从两者的变化趋势反向可以看出,当清晰图像由于烟雾增加,变得模糊时,其全变分值会相应的变小,烟雾越大图像越模糊,其全变分值越小。
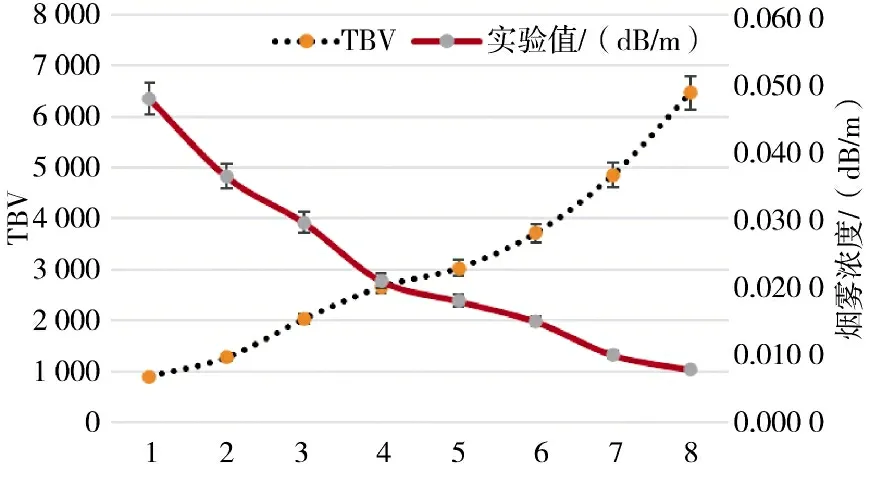
图1 全变分和烟雾浓度的关系
3.2 烟雾浓度的确定
Nicolas 于2006 年给出了亮度曲线与消光系数的关系,如图2 所示,横轴表示距离,纵轴表示亮度值。图中,L~L为5 条亮度曲线,其对应的消光系数分别为k~k。图中,消光系数有如下关系:
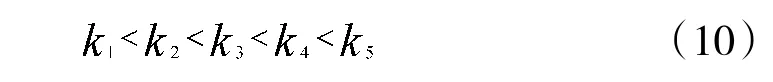
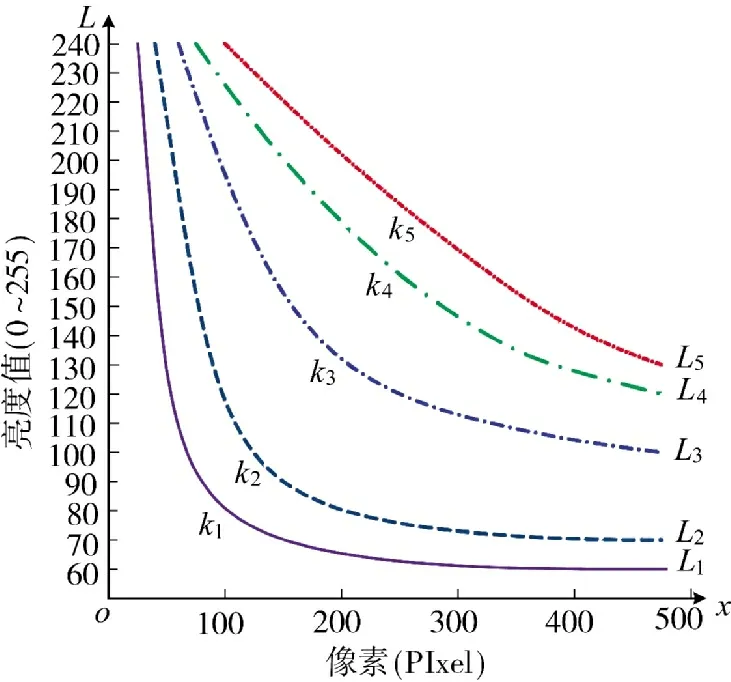
图2 亮度曲线与消光系数
而对应的烟雾浓度(以Con 表示)有如下关系
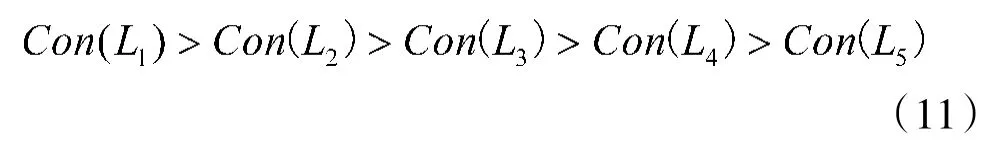
可以看出,烟雾浓度越高,亮度曲线的弯曲度越高。反之,烟雾浓度越低,曲率越低。实验数据显示,0.015 dB/m 以内烟雾浓度条件下,其视频图像的亮度曲线与图中L和L接近,即曲线相对平缓,这一特征为本文的算法实现提供了可能。
基于全变分的特征性质,可以将边界之间的差异有效表征出来。烟雾浓度升高时,变分会下降,所对应的消光系数会升高,即图中L所对应的总有界值低于L对应的变分值。根据现有理论,L 是一个单调递减的曲线,则可以视L、k 为待定系数,在变分基础上,对L 曲线进行拟合。当拟合值接近L时,可以得到消光系数k。
根据式(2),对于不同位置,即k 不断变化,有对应的L,如式(12)所示:
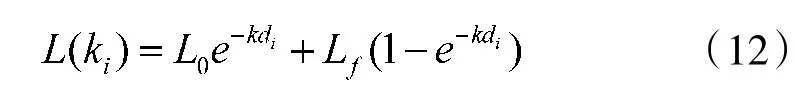
在式(12)基础上,建立目标函数得公式:
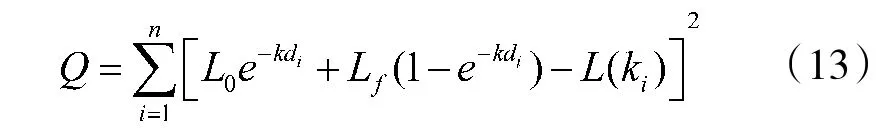
其中,n 为采样次数。进而求得目标物自由亮度L和消光系数k,即公式:

在此基础上,通过拟牛顿迭代法,进行多次迭代,能够得到消光系数。
基于全变分的烟雾浓度检测算法流程,如图3所示。
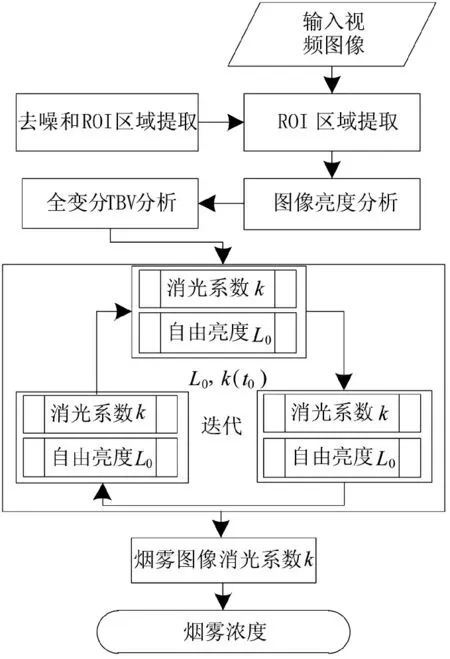
图3 系统流程图
衡量烟雾浓度检测算法优劣的指标依据多样,本文选择平均绝对相对误差,以验证基于全变分的烟雾浓度检测方法在估计环境烟雾浓度方面的优劣性。平均绝对相对误差计算公式为:
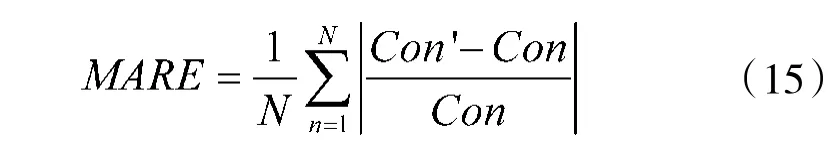
式中,Con'表示检测值;Con 表示参考值,一般用基于仪器观测值作为参考值。
4 实验与分析
为验证基于全变分的烟雾浓度检测算法的可靠性和有效性,选用利用浓雾渐变的实测视频数据验证分析,检测出其烟雾浓度值,并与仪器参考值做比对。
4.1 TBV 值与烟雾浓度的拟合
基于监控视频,采集场景,场景属于浓烟雾变淡的过程,对这一过程中,图像的TBV 值进行计算,并得到与其对应的烟雾浓度。
结果如图4 所示。图中纵轴表示TBV 值,横轴表示烟雾浓度值。从图中可以看出,在烟雾浓度比较高的时候,TBV 的值也比较低。这是因为,整个环境覆盖了烟雾,相当于噪声叠加于清晰视频图像,因此,缩小了图像边界之间的特性差异,从而导致TBV 变小。当浓烟雾变淡,实际上是一个对视频图像去噪的过程,当烟雾变淡或者消失后,从而与相对应的图像边界之间特性差异便显现出来。从图中可以看出,此时的TBV 值均增大,这一点和图4 所示也是一致的。
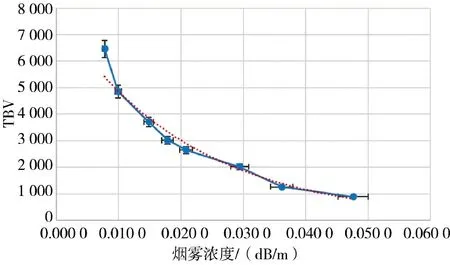
图4 烟雾图像TBV 与其烟雾浓度之间的关系
4.2 亮度曲线逼近
基于全变分的烟雾浓度估计算法,将含有烟雾浓度信息的图像视为模糊图像,结合图像特性,给出亮度曲线。首先基于全变分原理,对亮度曲线进卷积和积分处理,继而迭代求得消光系数k。若消光系数求得准确,则烟雾浓度估计也将准确。为了检验消光系数的求解是否准确,还需要进一步检验,方法是将目标物亮度估计值与观测到的目标物亮度实际值不断地做逼近比较。待目标物亮度估计值与实际值相近,或逼近误差很小时,则认为得到的消光系数k 较为准确。
若干目标物亮度曲线拟合比较,如下页图5 所示。由图5(a)与图5(b)可见,逼近效果较好,估计值与实际值基本接近。这两幅图的消光系数参考值分别为0.025 7 和0.021 8,实验值分别为0.026 3 和0.022 4。相对于前两幅,图5(c)的逼近效果较次。这3 个图的平均绝对相对误差分别为3.72%,4.36%,6.14%。
由图5 可以看出,在烟雾浓度较小时候,尤其是本文算法可以较好地逼近目标物亮度曲线。随着烟雾浓度增加,由于亮度曲线的曲率增加,逼近误差也随之增加,于是估计误差也加大。数据显示,最小的误差为3.42%,最大误差为9.29%,在国家规定的10%以内。

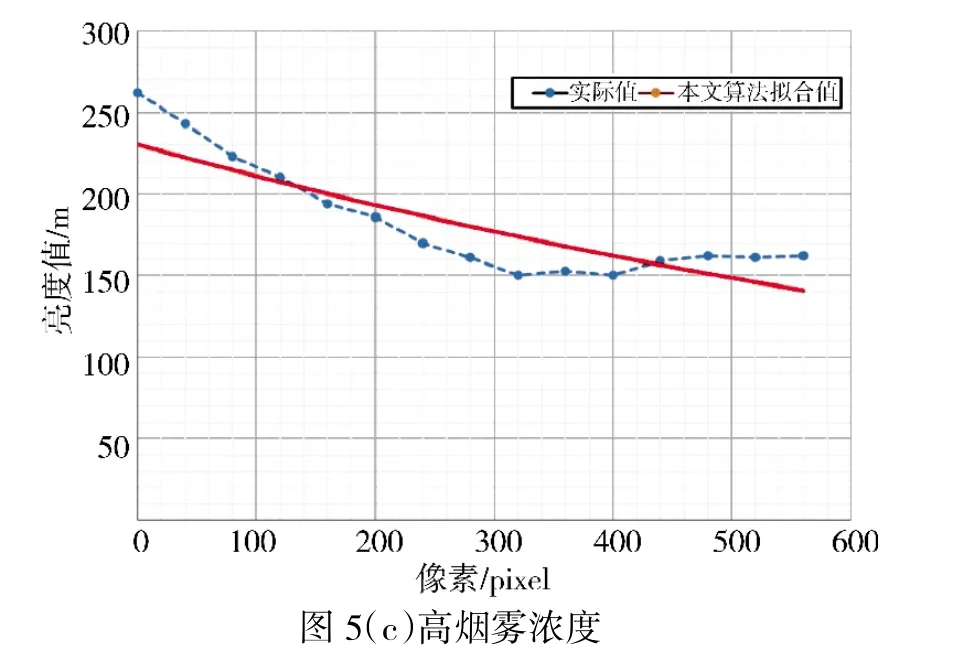
图5 目标物亮度曲线拟合比较
4.3 结果分析
为了验证基于全变分方法和分段平稳时间序列的大气烟雾浓度估计方法的性能,以烟雾逐渐变化的监控视频为例进行算法分析。
从参与烟雾浓度值与变分法烟雾浓度值的估计结果进行了比较。如图6 所示,显示了6 个有雾和朦胧的图像帧。消光系数值被标记在右上角,分别是0.047 6(dB/m)、0.036 1(dB/m)、0.029 4(dB/m)、0.020 8(dB/m)、0.014 9(dB/m)。用于变分进路验证的计算机硬件配置为CPU Intel (R)Core(TM)i7-8550U CPU @ 1.80 GHz 2.00 GHz,16 G RAM,双显卡。对监控视频进行去噪处理后,从视频帧中提取亮度曲线,并计算消光系数。共进行了300 个测试样品,估计误差在10%~15%之间的样本数为5。其他样本的误差均小于10%,全变分方法的测试结果符合要求。

图6 烟雾浓度不同的道路点
图7 列出不同烟雾浓度区间内误差对比,间隔分别为[0,0.02),[0.02,0.04),[0.04,0.06],采用全变分方法对8 个道路点的数据进行检验,将结果与参考标准值进行比较,只有一个相对误差在10%左右,其他误差均小于10%。本文算法绝对误差作图,在0.025 dB/m 以下,相对误差为6%以内。在烟雾浓度为0.05 dB/m 时,此时平均相对误差为12.09%。本文算法与传统的烟雾浓度检测误差比较如表1 所示。由表可见,文章所提算法具有较好的检测效果。
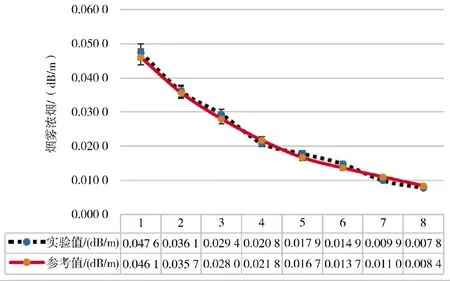
图7 算法绝对误差与参考值比较

表1 本文算法与传统算法误差对比
5 结论
环境天气状况,尤其是烟雾浓度,对很多行为影响特别大。基于全变分的烟雾浓度检测方法,通过提取等时间间隔监控帧,对含有烟雾浓度信息的图像进行分析,在Koschmieder 所提的烟雾浓度理论公式基础上,将消光系数由常数变量视为时间的函数,并构建泛函,通过全变分原理,继而基于分段平稳思想,对亮度曲线进行逼近,求得消光系数,估算出实时的烟雾浓度值。该算法充分利用侦察监控采集的图像,屏蔽了对烟雾静态特征的复杂计算,避免了繁琐计算带来的误差,验证效果显示,算法具有可操作性高、灵活性好等特点。

