基于改进SAMP 的UFMC 信道估计算法*

刘子昌，张锁良

（1.陆军工程大学石家庄校区装备指挥与管理系，石家庄 050003；2.河北大学电子信息工程学院，河北 保定 071002）

0 引言

语音、视频和网络等多种传播方式极大地丰富了人们日益增长的精神文化生活。然而，随着移动数据流量呈指数级增长，第五代（fifth generation，5G）通信系统必须能够支持多样化的流量类型。文献［2］首次提出UFMC 作为一种新的基于非正交波形的5G 系统空口技术，结合了正交频分复用（orthogonal frequency division multiplexing，OFDM）的简单性和滤波器组多载波（filter bank multi-carrier，FBMC）的鲁棒性等优点。与FBMC 相比，UFMC要求的滤波器长度更短，使得系统中接收机的复杂性降低。与OFDM 不同，UFMC 不必插入循环前缀（cyclic prefix，CP），通过改变符号的边缘下降特性和在子带中过滤每组载波来减少带外功率和滤波器的长度。UFMC 因其传输效率高、单抽头频域均衡和抑制带外数据泄漏而受到越来越多的关注，这些特点促使UFMC 更适合短上行突发通信和低延迟通信。

信道估计是无线通信系统中一个关键的任务。由于传统的信道估计方法未考虑无线信道具有稀疏性，导致信道估计过程的导频开销较大。而基于压缩感知（compressed sensing，CS）的信道估计技术可以在提高信道估计性能的同时减少导频开销。常用的CS 信道估计方法有正交匹配追踪（orthogonal match pursuit，OMP）和正则化正交匹配追踪（regularized orthogonal match pursuit，ROMP）等。虽然上述算法易于实现且重构精度高，但是使用上述算法的前提是预知信道稀疏度，而SAMP 算法可以在未知稀疏度的情况下，自适应地对信号进行重构。针对SAMP 算法的不足，文献［10］中提出了通过预处理先验信息，以减少算法中的迭代次数。文献［11］中提出了一种基于降噪回溯的SAMP 算法，结合降噪技术，提高重构精度。

本文为解决SAMP 算法在停止迭代时需要对噪声参数先验估计的问题，并进一步提升信道估计的准确度，提出基于改进SAMP 的UFMC 信道估计算法。该算法将Dice 原子匹配准则替代原有的内积准则，通过设置模糊阈值预先选择原子完成具有高相关性原子的筛选，并对停止迭代的判决条件进行优化，以达到不需要进行噪声参数先验估计的目的。通过仿真实验分析，该算法可避免噪声参数的先验估计，并进一步提升信道估计的准确性。

1 UFMC 系统简介

UFMC 在OFDM 的结构基础之上传输带宽被划分为B 个子带，通过N 点离散傅里叶逆变换，将频域信号S（k）转化为时域信号s（n），公式表示为：

其中，K表示第i 个子带包含的子载波数。FIR 滤波器的长度为L，UFMC 信号与FIR 滤波器进行卷积运算后长度为N+L-1。将来自子带滤波器的信号叠加在一起后，得到时域传输信号。UFMC 发送信号为：

其中，x（n）为UFMC 系统的发射信号；*表示线性卷积运算；f（n）表示第i 个子带所使用的FIR 滤波器f的系数。

UFMC 符号通过带有信道脉冲响应h（k）的无线信道后可表示为：

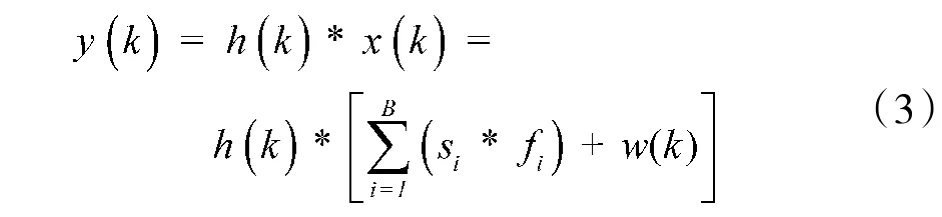
在接收机处，接收到的射频信号叠加所有用户传输的噪声后被转换到基带。通过离散傅里叶运算将时域信号转为频域信号，输出Y（k）为：

假设FIR 滤波器设计合理，因此，系统性能主要受到噪声限制，接收信号可写为：

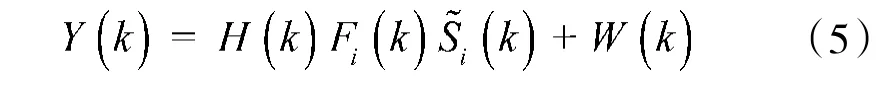
2 UFMC 信道估计

2.1 CS 理论

已有研究表明，由于无线信道具有稀疏性，因此，UFMC 系统的信道估计可以应用CS 技术。CS技术能够以低于Nyquist 要求的速率同时完成采样和压缩，降低导频开销，对原始信号实现高概率重构。因此，与传统的信道估计算法相比，CS 更适合UFMC 系统。

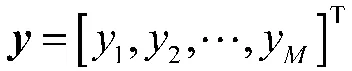
可以通过线性规划对式（9）描述的优化问题进行求解。在原始信号的重构中，贪婪算法由于计算复杂度低且易于实现而得到广泛应用，其主要思想为通过在迭代中寻找局部最优解进而向全局最优解靠近。

2.2 SAMP 算法

在稀疏度未知的情况下，SAMP 算法是最具代表性的对原始信号进行重构的算法。该算法引入步长s 和阶段值stage 的概念，通过更新迭代的残差进行调整并对原始信号进行重构，同时引入了回溯思想进行原子筛选提高估计精度。SAMP 算法的具体步骤如下所示：

输入：传感矩阵A，观测向量y，步长s。

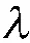
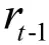
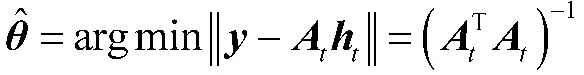
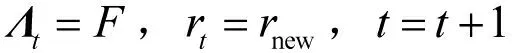
2.3 基于改进SAMP 的算法

通过分析可知，采用算数平均值的Dice 原子匹配准则可以有效解决几何平均值的不足。因此，改进后的算法使用Dice 原子匹配准则来改善上述内积准则的不足。改进后匹配准则能够准确选择出高度相关的原子，提高信号重建的准确性。Dice 系数可表示为：

由于现有SAMP 算法在原子预选过程对向量u中各元素值进行由大到小的排序后，固定地选取前l 个最相关的分量，因此，所选相对靠后的原子实际上相关性较低，引入不合适的原子对算法的重建精度有着不利影响。改进后的算法通过设置模糊阈值来进行初选原子操作用于解决上述问题，可以去除掉不理想的原子。在选择适当的阈值参数α 后（α 通常取0.5～0.7），所选择原子的相关性均大于ασ，从而可以选择出具有高相关性的原子。

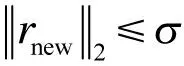
改进后的算法具体步骤如下，流程图如下页图1 所示。

图1 改进后算法的流程图

输入：M×N 维传感矩阵A，M×1 维观测向量y，步长s，阈值参数α。

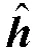
1）初始化：迭代索引值t=1，阶段数stage=1，残差r=y，步长，选择原子数量为每步步长的整数倍，索引集Λ=覫；

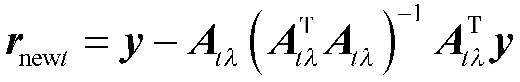
3 仿真结果和分析

使用MATLAB 对UFMC 系统的信道估计算法进行仿真，主要分析在不同算法下UFMC 系统的均方误差和误码率。将本文提出的基于改进SAMP 的UFMC 信道估计算法与OMP 算法、压缩采样匹配追踪（compressive sampling match pursuit，CoSaMP）算法、SAMP 算法和文献［20］所提算法进行对比，验证本文改进后算法的有效性。

仿真实验中的参数设置如表1 所示。

表1 仿真参数

各算法在不同稀疏度下的恢复概率及阈值参数α 的取值对所提改进后算法的恢复概率影响情况如图2 所示，阈值参数取值范围通常为0.5～0.7，间隔0.1 取值。

图2 不同观测值数量下各算法的恢复概率

仿真结果是进行1 000 次实验统计出的恢复概率，使用128×256 的高斯矩阵为测量矩阵，设置256×1 的稀疏信号作为原始信号，对比SAMP 算法、文献［20］所提算法和本文改进后算法在不同稀疏度下的恢复概率。可以看出，改进后的算法在阈值参数α=0.7 的情况下恢复率最差，在阈值参数α=0.6 的情况下具有最优的恢复率，并且α=0.6 时的重构效果与改进前的算法及文献［20］所提算法相比明显要好。可以推断出阈值参数α=0.6 是较好的值，所以在接下来的仿真中阈值参数取α=0.6。

图3 和图4 为导频数取32 时，不同信噪比下OMP 算法、CoSaMP 算法、SAMP 算法、文献［20］所提算法和本文所提改进算法的均方误差和误码率对比情况。

图3 不同信道估计算法的均方误差性能对比

图4 不同信道估计算法的误码率性能对比

由图3 和图4 可得，UFMC 系统中不同信道估计算法的均方误差和误码率随着信噪比的增加而逐渐降低。OMP 算法的估计精度与图中其他算法相比最低，其次是CoSaMP 算法以及SAMP 算法。本文所提改进后的算法由于对原有SAMP 算法的不足进行改进，使得本文所提改进后的算法性能与现有算法相比是最优的。改进后的算法相比于SAMP 算法性能提升大约1 dB～3 dB，且与文献［20］所提算法相比可获得约1 dB 的性能增益，具有更加优秀的重构性能，改善了信道估计的准确度，且可以避免噪声参数的先验估计，证明了理论分析是正确的。

4 结论

本文主要研究了UFMC 系统的信道估计问题，针对直接将SAMP 算法用于UFMC 系统时停止迭代需要噪声参数先验估计的不足，提出了基于改进SAMP 的UFMC 信道估计算法。所提算法使用Dice原子匹配来对内积准则的不足进行改善，通过设置模糊阈值来进行初选原子的操作，最后对停止迭代的判决条件进行优化。经实验验证，所提算法可以在避免进行噪声参数先验估计的前提下，提升信道估计的准确度。