基于非接触式电流传感器的电力系统拓扑识别方法
王炳焱陈锦荣唐军沛冯仁杰
(1.广东电网有限责任公司佛山供电局,广东 佛山 528000;2.东方电子股份有限公司,山东 烟台 264670;3.哈尔滨工程大学智能科学与工程学院,黑龙江 哈尔滨 150000)
正确的电网拓扑对于配电系统的状态估计、故障定位、需求响应等至关重要。如果对拓扑识别错误,则系统的控制和运行会产生偏差[1]。因此,必须经常识别网络的拓扑。然而,由于配电网线路上的测量数据有限,以及获取的开关和断路器状态信息往往不可靠[2-4]。在实际应用中,拓扑识别最常见的方法是派遣电网运维人员检查开关状态,但人工成本很高,而且不能为了持续跟踪拓扑的变化而频繁地执行这类操作。另一种方法是使用基于测量的拓扑识别算法,该算法根据可用的传感器数据估计开关的状态。
一些学者提出了基于测量的拓扑识别方法[5-10]。其中一类方法利用各种现场测量值对每种可能的拓扑结构进行状态估计,然后选择状态估计残差最小的拓扑结构[11]。然而,这种穷举的方法通常在计算上很复杂。另一类方法是将拓扑识别问题集成到状态估计问题公式中,以同时估计系统状态和开关状态[12],这有助于提高计算效率。但是,任何涉及状态估计的拓扑识别算法都会遇到可能没有足够的现场测量值来进行完整状态估计的问题。
还有一些学者提出了使用有限测量的拓扑识别方法。其中常见方法是基于电压测量的拓扑识别[13-15]。例如,在文献[16]中,作者通过对电压测量进行相关性分析来重建电网拓扑。在文献[17]中,采用时序信号验证方法,利用同步电压相量数据来识别拓扑结构。还有一些方法是使用智能电表数据进行拓扑识别[18-21]。也有基于测量线路潮流的拓扑识别方法[22-23]。但在实际应用中,每个测量点都需要安装电压互感器和电流互感器之类的仪器设备进行功率测量,造价昂贵。
本文提出了一种新的基于非接触式电流传感器的拓扑识别算法。首先以混合整数非线性规划(mixed integer nonlinear programming,MINLP)的形式提出了拓扑识别问题。然后采用重构方法来处理非线性问题,将其表述为混合整数线性规划(mixed integer linear programming,MILP)。此外,还对非接触式线路电流传感器的规划提出了建议,以确保拓扑识别方法的性能。
文中研究内容基于非接触式传感器的应用,与传统的测量电压和功率的传感器相比,非接触式电流传感器具有成本低、安装简单的优点。非接触式传感器还可以测量电场,估计电流测量的相对相角,从而可以像微型相量测量单元(phasor measurement unit,PMU)一样估算相量,但其只能估算电流。这类传感器可测量大于1 mA 的电流,误差为1%,测量相角的误差为1.5°[24]。非接触式电流传感器已经有了大量商业应用,越来越多的电网公司正在考虑在其配电线路上安装这种低成本传感器。
在下文中,第1 节介绍了拓扑识别方法。在第2节对非接触式电流传感器的规划及误差处理进行了分析。在第3 节以33 节点测试系统和位于某地的实际运行系统为例,对所提出的方法进行了测试,并与其他方法进行比较。最后在第5 节给出了结论。
1 拓扑识别方法
1.1 拓扑识别问题的非线性表达
假设所有开关都闭合,所有线路和节点都处于正常工作状态。根据基尔霍夫电流定律(Kirchhoff’s Current Law,KCL),注入到每个节点的电流等于连接到该节点的线路相关电流之和。

式中:Ii为注入节点i的电流变量,Ni为连接到节点i的线路集合,Iij为线路{i,j}的电流变量,N为节点集合。在两个节点之间的线路上流动的电流取决于线路的开关状态、两个节点的电压和线路的导纳。根据基尔霍夫电压定律(Kirchhoff’s Voltage Law,KVL),可得:

式中:sij为线路{i,j}切换状态的二进制变量,Vi为节点i的电压变量,yij为线路{i,j}导纳。如果线路{i,j}在正常工作状态,则sij=1,否则为0,确保Iij为0,表示该线路已停止工作。根据幂法则,节点电压Vi与电流Ii之间的关系可表示为:

式中:bi为用于节点i切换状态的二进制变量。如果节点i连接到网络,则bi值为1,否则为0,表示存在孤岛节点。在这种情况下,拓扑识别算法可以确定停电区域。拓扑识别问题可用以下优化问题的形式表示:
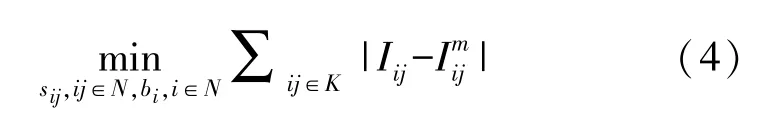
式(4)受式(1)-(3)约束,其中K表示装有电流传感器的线路集合。在上述优化问题中,主要决策变量是二进制线路切换状态变量sij和二进制节点切换状态变量bi。其他变量,即线路电流Iij、节点注入电流Ii和节点电压Vi是辅助变量。负载Si和线路电流测量为参数。优化问题关键在于使得由式(1)~式(3)计算的线路电流相量与线路传感器测量的线路电流相量相匹配。线路sij的解可得到线路开关的状态,因此sij的解可指明拓扑结构。节点i的变量bi的解指示节点是否连接到电网的其余部分,bi的解指明停电区域,辅助变量的解表示对系统状态的估计。
1.2 拓扑识别混合整数线性规划表达
式(4)所示的优化问题在其目标函数和约束条件中都涉及几个非线性项。以下将分析如何将这个问题转化为MILP 形式。
步骤1 式(2)中的非线性是由于二进制变量sij与连续变量Vi和Vj相乘所致。为了克服这种非线性,首先,用下面的线性方程代替式(2):

式中:Uij是辅助变量,相当于sij(Vi-Vj)。如果sij=1,即线路{i,j}在工作中,则Uij=Vi-Vj,否则Uij=0。Uij、sij和Vi-Vj之间的非线性关系通过添加以下新的线性约束来处理:

上述约束式中M为大M法参数。由于Uij和Vi-Vj是复数形式,因此使用式(6)~式(7)和式(8)~式(9)分别得到Uij的预期实部和虚部。如果sij=0,则式(6)和(8)不具有约束力,且由式(7)~式(9)可得Uij=0,再根据式(5),可得Iij=0。如果sij=1,则式(7)和(9)不具有约束力。由式(6)~式(8),可得Uij=Vi-Vj,再考虑式(5),可得Iij=yij(Vi-Vj)。由此可知式(5)~式(9)中的线性约束与式(2)中的非线性约束等价。
步骤2 式(4)中的非线性与式(3)中电压相量、电流相量相乘有关,称为潮流方程非线性。采用了文献[25]中基于泰勒展开和工程近似的方法来处理此类非线性问题。为此,与传统潮流公式中的实数近似不同,采用复数线性近似。假设每个节点i上的电压以标幺值表示,与变电站的基准节点上的电压相关。假设:

通过在零附近进行泰勒级数展开并忽略高阶项,可得:

近似误差的计算公式为:
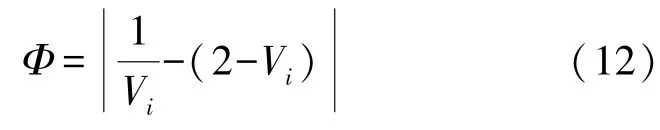
图1(a)表示复数域中的电压相量,在图1(a)中圆内每个点上评估上述误差,从而得到图1(b)中所示的误差指标。在ΔV=0.1 时,近似误差仅为1%左右。实际上,ΔV通常是0.05 或更小。因此,近似误差仅为0.3%或更小,可以忽略。

图1 线性化的准确性验证
接下来,将式(11)代入式(3)可得:

由于二进制变量bi与相量变量Vi的相乘,式(13)仍然是非线性的。因此,引入一个新的辅助变量Wi,并将式(13)替换为以下线性方程:

式中:Wi=Vibi。如果bi为1,即如果节点i连接到电网,则Wi=Vi;否则Wi=0,表示该节点没有连接到电网。上述Wi、bi和Vi之间的关系可以通过实施以下新的线性约束来实现:

如果bi=1,则Re{Wi}=Re{Vi};如果bi=0,则Re{Wi}=0。类似地,根据式(17)~式(18)可得到Wi的虚部。式(14)~式(18)中的线性等式与式(3)中的非线性等式约束等价。
从式(14)开始,与断开的节点相关联的电流注入被约束为0。然而,并未要求断开节点的电压也为0。还需要添加以下新的约束,以确保断开的节点确实为零电压:

步骤3 式(4)中的目标函数是一个绝对值,它不是线性的。可用一个线性目标函数和几个线性不等式约束代替目标函数中的绝对值约束。式(4)中的目标函数最小化等价于最小化的实部和虚部.设Eij和Fij表示两个辅助变量,其中|Re{Iij-通过以下约束将辅助变量集合到问题中:
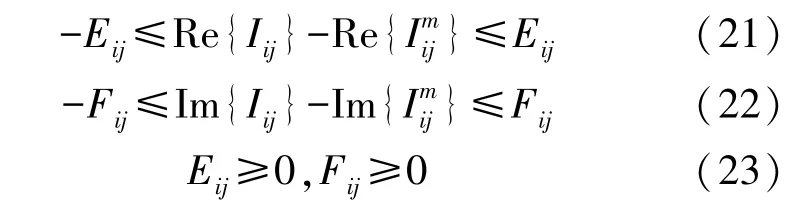
步骤4 结合步骤1 到3,将拓扑识别优化问题以线性形式表示如下:
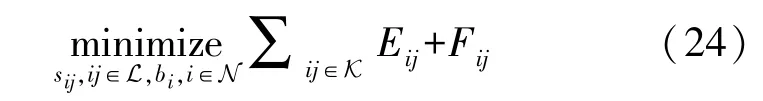
式(24)以式(1)、式(5)~式(9)和式(14)~式(23)为约束。拓扑识别问题已被表述为MILP 问题,可以使用各种软件包进行求解。
2 电流传感器配置
2.1 可观测性与传感器布置
为了识别电网拓扑,需要确定开关状态。开关断开的线路无电流,因此可通过估计线路电流来获得开关的状态,从而获得最终的拓扑结构。可观测性分析需要确定多少个传感器以及安装位置才能估计所有线路的电流。
定理1 如果在配电网的每个独立回路中至少放置一个线路电流传感器,则配电网的拓扑是可识别的,即可以求解式(4)以得到正确的拓扑。
证明在具有N个节点和L个支路的电路中,为了估计支路电流,需要L个独立方程。在可用的N个电流方程中,N-1 方程是独立的。因此,为了得到总共L个独立方程,需要L-(N-1)个附加独立方程,可通过测量L-(N-1)个线路电流来获得。
回路是一条闭合路径,它从一个节点开始,经过一组节点,然后返回到初始起始节点,而不会多次经过任一节点。如果一个回路本身不包含任何回路,则称它是独立的。在电路理论中,独立回路产生独立的KVL 方程,其个数为L-(N-1)。因此,只要使用线路电流传感器直接测量独立回路中L-(N-1)条线路的电流,就可以估计出所有线路电流。
在图2 所示的独立回路中,假设节点流入电流I1,I2,…,In已知。要计算回路中每条线路的电流I1,2,…,In-1,n。由KCL 可得:
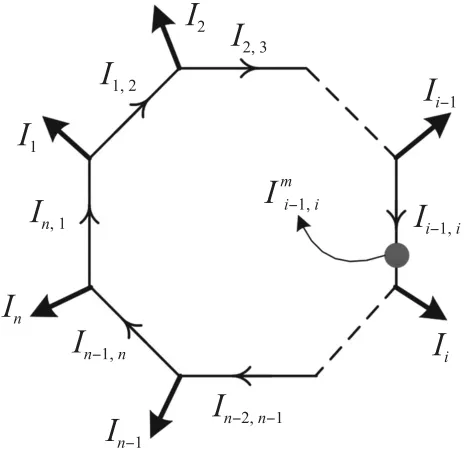
图2 具有n 个节点的独立回路

其中A是n×n矩阵。矩阵A的秩为n-1,因此,线路电流存在无穷多个解。然而,如果用一个基于线路电流传感器测量的独立方程代替其中一行,可保证这个线性方程组具有唯一解。替代公式为Ii-1,i=,其中表示在节点i-1 和节点i之间测得的线路上的电流,得到以下新的线性系统:

与式(25)不同,式(26)中的方程组有唯一解。因此在独立回路中的任何位置安装一个线路电流传感器将提供一个独立方程。由于网络中存在L-(N-1)个独立回路,因此在每个独立回路上安装L-(N-1)个线路电流传感器就可解决线路电流估计问题。
在如图3 所示的具有4 个节点和5 条线路的网络中,回路ℓ1和回路ℓ2是两个独立的回路,节点电流I1、I2、I3、I4已知,线路电流I1,2、I1,3、I2,3、I3,4、I4,1未知。此网络的KCL 方程为:

式中:矩阵A的秩为3,为了确定5 个线路电流的唯一解,需要向矩阵A再添加2 个独立行,在两个独立回路ℓ1和ℓ2上安装一个线路传感器来实现。在传感器安装位置的10 种可能组合中,有8 种组合测量了两个回路中的电流,如表1 中的组合3 到5 所示,这些结果与定理1 一致。如果两个独立回路共用一条线,例如图3 中在回路ℓ1和ℓ2之间共用线路{1,3},则在这种共用的线路上放置一个传感器来提供一个新的独立方程。采用文献[26]中算法来识别独立回路,以便在每个独立回路上放置传感器。
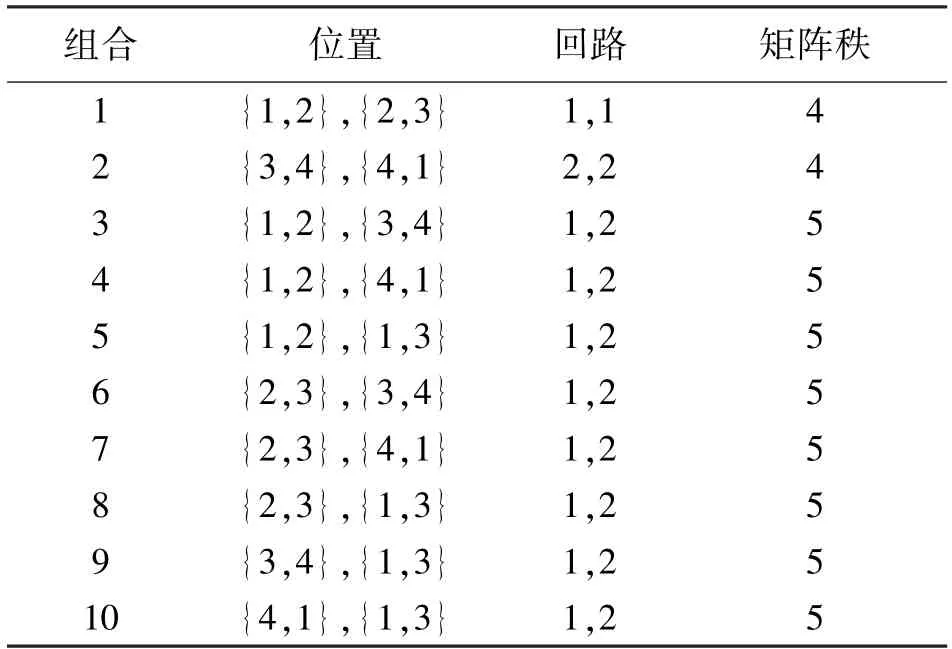
表1 图3 中网络的传感器放置组合场景
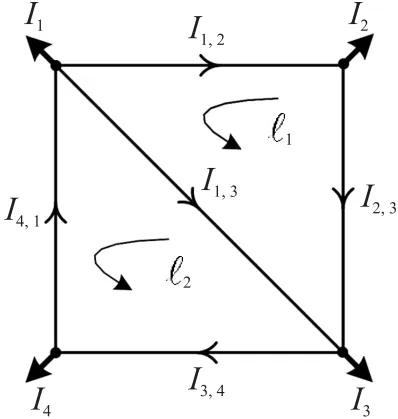
图3 具有4 个节点和2 个回路的网络
2.2 测量误差处理
为了处理测量误差和伪测量误差的影响,需要对式(24)进行调整。将式(1)中的注入电流约束以惩罚项的形式移动到目标函数中,可得:
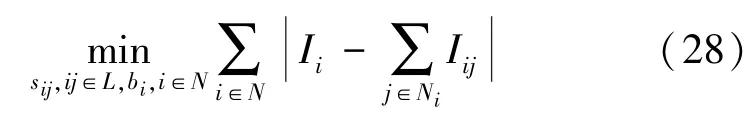
采用与第1.2 节中所述步骤3 类似的方法,通过定义辅助变量Gi和Hi,并添加以下新的线性约束来处理新的非线性:

在存在测量误差和伪测量误差的情况下,拓扑识别问题可以表示为如下的MILP:

2.3 多周期优化
拓扑识别算法通常基于单个周期的测量值,然而在实际应用中,线路电流测量值可能在拓扑改变后的初始时刻后继续可用,即使使用了高精度的线路传感器,但伪测量误差依然存在,而以多周期优化的形式运行拓扑识别算法,可减轻测量误差和伪测量误差的影响。T表示测量和伪测量的可用测量周期数量。[t]表示对应于每个周期t的测量数据。Ψ[t]表示式(32)中基于周期t的数据的目标值。多周期形式的拓扑识别问题可以表示为:
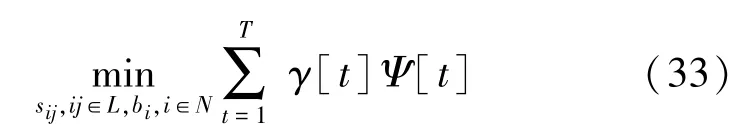
式(33)受式(5)~式(9),式(14)~式(23),式(29)~式(31)约束。γ[t]表示与周期t测量值相关联的概率。式(33)中隐含的假设是所有测量值都与相同拓扑关联,即在测量周期1 至T期间,拓扑不发生改变。一旦检测到拓扑改变,多周期拓扑识别算法将被重置。在文献[28-29]中已经介绍了几种检测拓扑变化的方法。
从原理上讲,拓扑识别是一种估计问题,它是根据给定的测量值和输入的伪测量值来估计开关状态。式(33)中的每个测量周期实质上为这样的估计问题提供了冗余。开关的状态从一个周期到另一个周期是固定的,然而由于每个节点上负载的随机性,测量和伪测量中存在随机变化。每个周期为这些随机变量生成一个新的随机场景,在估计开关状态时提供冗余。如果跨不同周期的随机性遵循均匀分布,则γ[t]=1/T,否则使用已知的非均匀概率分布。
3 案例分析
3.1 33 节点测试系统
将所提出的拓扑识别方法应用于图4 所示的33 节点测试系统来证明该方法的有效性,相关数据见文献[24]。线路4,6,7,9,10,11,12,14,15,16,17,18,26,28,30,32 开关为常闭状态,其余线路开关为常开状态。常开开关是用虚线表示的五条线。由于该网络中有21 个开关,因此可以创建221 种不同的拓扑,选择其中65 种拓扑配置进行测试,包括50 个放射状拓扑、10 个环状拓扑和5 个孤岛拓扑。

图4 33 节点系统示意图
一旦五条联络线处于闭合状态,就构成五个回路:ℓ1,…,ℓ5。如在3.1 节所述,每个回路必须使用至少一个线路传感器进行测量,以满足拓扑识别的要求。本案例中五个电流传感器的位置选择如图4中的圆点所示。除了电流测量外,还假设所有节点上的负荷均可通过伪测量获得。
在MATLAB 中进行了网络仿真和拓扑识别算法的实现,并用IntLinProg 函数求解了式(24)、式(32)和式(33)中的优化问题。在测试中,测量结果如下所示:


这保证99.7%的ei值落在真实值的±ηi%内。此外,拓扑识别算法的精确度以百分比表示:
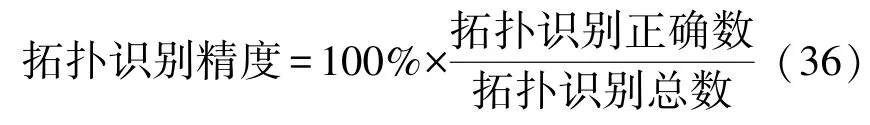
3.1.1 线路电流测量误差
电流传感器通过测量电场来得到相对相角。传感器电流大小的误差为1%~3%,电流相角的误差为1°~5°。表2 给出了在考虑线路电流测量误差的情况下拓扑识别算法的结果。实验结果表明,在几乎所有的误差水平下,准确率都在99%以上。因此,所提出的拓扑识别算法具有较强的鲁棒性。

表2 拓扑识别算法精度
3.1.2 伪测量误差
伪测量值通常是通过智能电表数据或历史数据进行短期负荷预测而获得的。通过使用蒙特卡罗方法生成不同的场景来检验所提出的拓扑识别算法。与伪测量相关的不确定度范围可根据可用信息而变化。可以通过聚合客户智能电表数据来获得这些伪测量值。或者,在没有计量数据的情况下,可以仅根据负载变压器的额定值进行估算。还可以使用计量数据和变压器额定值进行组合估算。对于不同伪测量值的获取方式,可能会带来较大范围的误差,当有智能电表数据时,误差低至10%[30],当仅根据变压器负荷分配来估计伪测量值时,误差高达50%。为了评估所提出的拓扑识别算法在各种可能的伪测量场景下的性能,在仿真中检验了上述两种误差范围。表3 给出了拓扑识别算法在不同伪测量误差水平下的精确度。如果误差被限制在30%以内,那么几乎可以确保正确的拓扑识别。但是,如果误差增加到50%,那么拓扑识别准确度就会显著下降,从而使拓扑识别结果不可靠。当然,在如此高的误差下,失去精确性不可避免。

表3 在不同伪测量误差水平下拓扑识别算法精度
3.1.3 多周期优化提高精度
误差的影响是可以通过利用测量数据的多周期优化在伪测量中补偿的。为了测试多周期拓扑识别算法的性能,使用文献[31]中的伪测量生成方法生成周期序列,其中我们基于正态概率分布生成伪测量误差,平均值为零,标准差如下:

然后,求解式(33)中的拓扑识别多周期优化,并且每当有新的测量周期可用时,更新拓扑识别结果,如图5 所示。随着更多的测量周期的出现,拓扑识别的准确度也会提高。即使在伪测量中有50%的误差,其中单周期拓扑识别算法的准确率为77.1%,多周期拓扑识别算法也可以在测量20 次后将准确率提高到95.0%。随着测量数量的增加,式(33)中求解多周期优化问题的计算复杂度增加。例如,对于10 次和20 次测量,多周期拓扑识别算法分别运行约40 s 和125 s,远远大于表3 中提供的单周期拓扑识别运行时间。
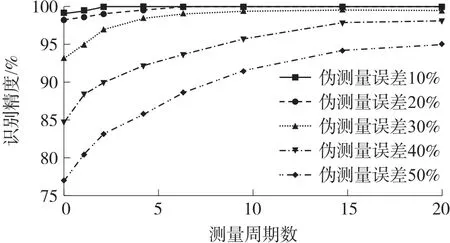
图5 多周期优化算法的精度
通过一个算例比较了单周期和多周期拓扑识别算法的性能,表4 中给出了结果。每次测量分别采用单周期拓扑识别算法。仅在四次测量(6、9、11 和13)中识别了正确的拓扑。在11 次测量中,单周期拓扑识别算法未正确识别拓扑,这是由于负载的变化和伪测量中的较大误差所致。
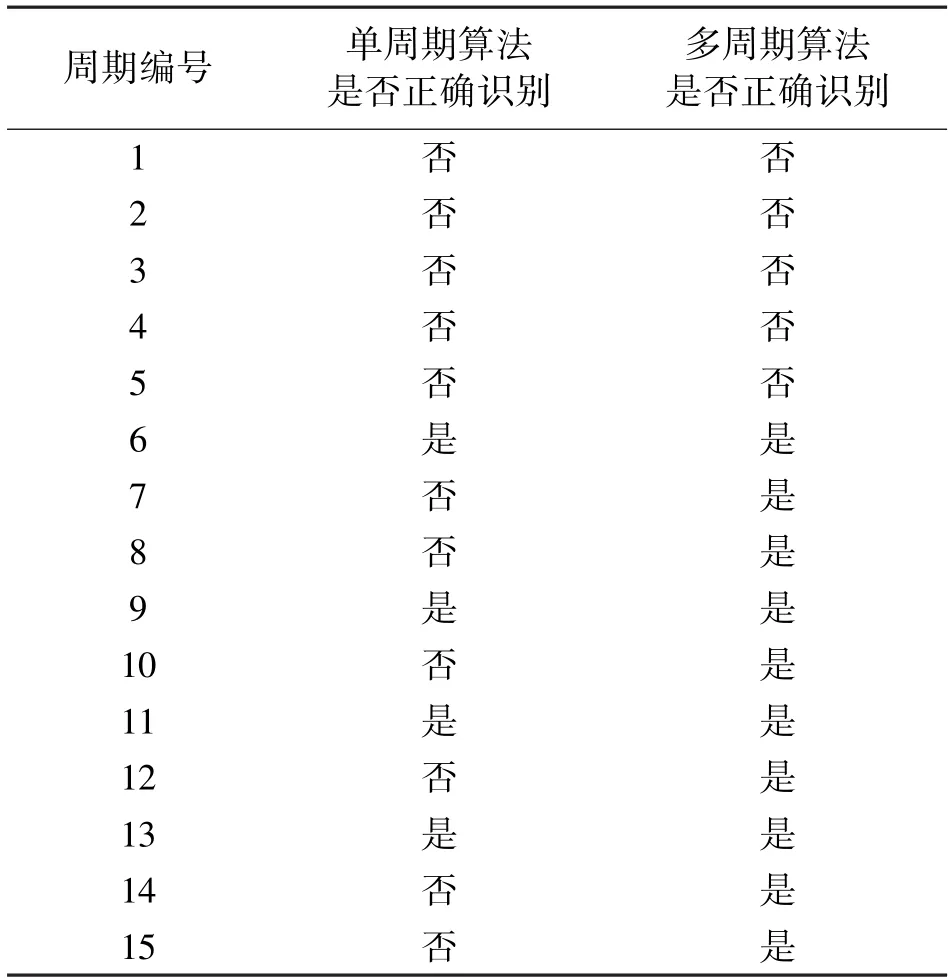
表4 单周期与多周期算法对比
相反,当使用多周期拓扑识别算法时,一旦有足够的测量可用,就能正确识别拓扑。当多周期拓扑识别算法应用于第一次测量时,它最初与单周期拓扑识别方法相同;然后,在第二次测量中,多周期拓扑识别算法应用于第一和第二测量组合;在第三次测量中,多周期拓扑识别算法应用于第一次、第二次和第三次测量组合;依此类推。随着前六次测量之外有更多测量可用,多周期拓扑识别方法在第6 至第15 次期间则可正确识别拓扑。
3.1.4 MILP 对比MINLP
MILP 和MINLP 在计算复杂性方面大致相似。然而在实际中,通常将MINLP 转换为MILP 可取得更好的效果。目前在MILP 求解器的开发方面已取得了相当大的进展,相比之下,MINLP 求解器还不够成熟,还未达到稳定可靠。此外,通过使用分支和定界等方法,MILP 求解器可保证得到精确的最优解。当考虑到所提出的拓扑识别优化问题时,式(4)中的拓扑识别问题实际上是一个非凸的MINLP。非凸MINLP 特别难求解,因为即使使用分支和定界等方法处理整数变量后,在每次迭代中要解决的仍然是一个困难的非线性非凸优化问题。
测试了三种求解器来解决式(4)中原始MINLP 问题:NOMAD,SCIP,和BONMIN。利用NOMAD,SCIP 求解器总是找不到可行解。假设伪测量误差为5%,BONMIN 正确识别出65 个拓扑中的10 个。对于这55个错误识别的拓扑,BONMIN 既找不到正确的解,也找不到任何可行解。表5 给出了在不同线路断开情况下,求解MINLP 得出的结果。只有一种情况接近最优解。因此,将MINLP 转化为MILP 是有必要的。
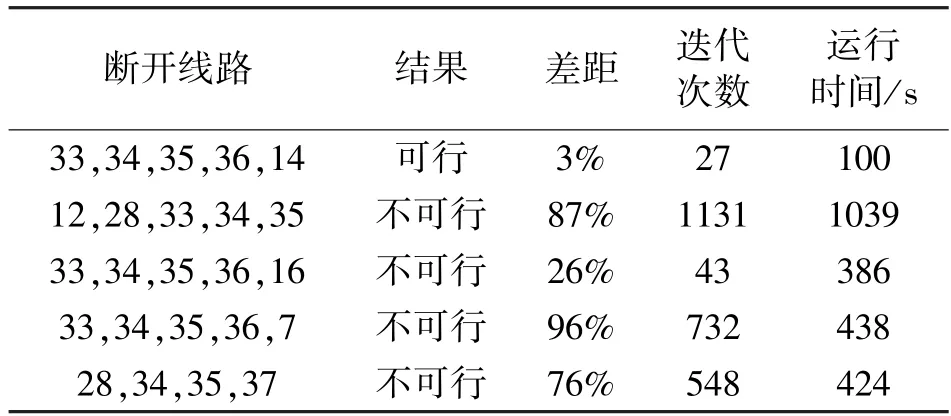
表5 MINLP 拓扑识别问题在不同情况下求解结果
3.1.5 性能对比
在本部分中,性能比较是在两个参考文献的基础上进行的。第一个是文献[32],其中的方法在本质上可以支持使用线路电流传感器,但它是基于电路连通性开发的,且不涉及潮流方程。结果如表6第三列所示。由表6 可知,文献[32]中的方法对伪测量误差高度敏感。
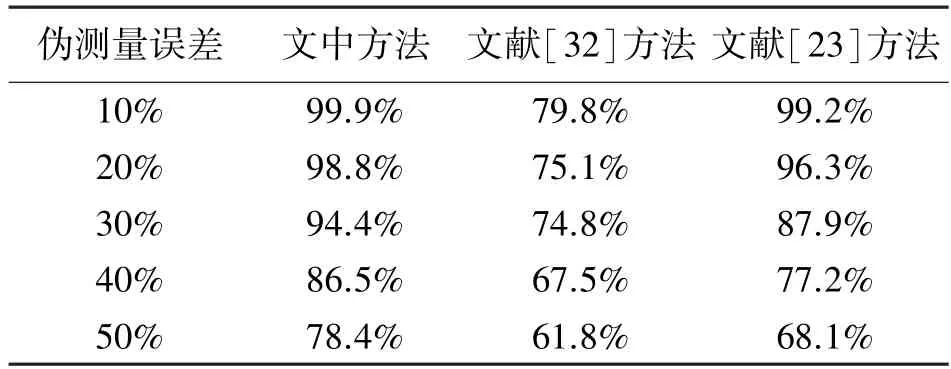
表6 不同拓扑识别算法的精度
第二个是文献[23],其中的方法与本研究中提出的方法本质上是类似的,但它使用了不同的目标函数,且进行的是混合整数二次规划(mixed integer quadratic programming,MIQP),而不是MILP。结果如表6 第四列所示。可以看出,这种方法的性能也随着伪测量误差的增加而降低。这是因为在MIQP中,最小化平方误差会将拟合值拉向不准确的伪测量值,而不是最小化绝对误差。此外MIQP 的计算时间要比MILP 的计算时间长得多。从成本效益分析的角度来看,文献[23]中MIQP 方法需要使用10条线路的功率传感器,实际应用往往非常昂贵和费力,而所提出的方法使用的是5 条线路的电流传感器,价格便宜,易于安装,但性能几乎相同,这体现了所提出的方法在成本效益方面的优势。
3.2 实际运行系统
将所提出的拓扑识别算法应用于某地的配电网。这个配电网大约有400 个节点和37 个开关,拓扑结构由13 个回路组成。假设在这13 个回路上安装13 个电流传感器。总共定义了20 种不同的拓扑。对配电网的精确模型进行了仿真,拓扑识别算法精度的结果如表8 所示。在较低的伪测量误差下,拓扑识别算法几乎成功地识别出所有拓扑。表8 中的结果与第3 节中33 节点测试系统的表4结果基本一致。
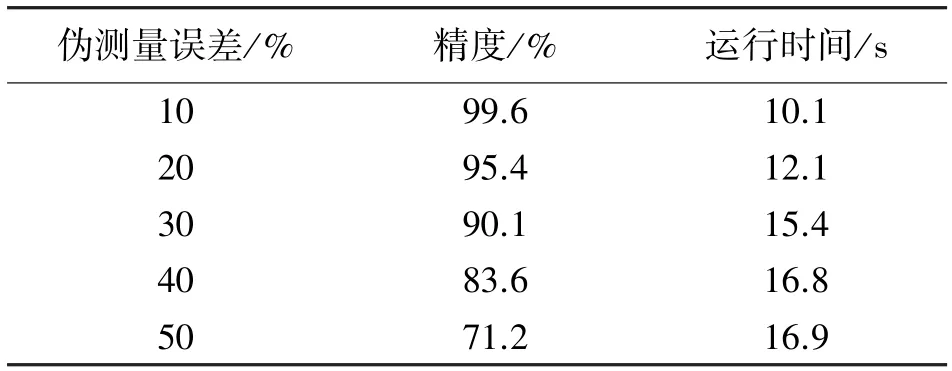
表7 在实际运行系统中拓扑识别算法精度
4 结论
提出了一种配电网拓扑识别方法,该方法基于一类新兴低成本非接触式线路电流传感器。设计出一种与上述传感器无法测量电压和功率这类局限性兼容的拓扑识别算法,同时算法的计算复杂度较低且易于处理,提出多周期算法对测量和伪测量中的各种误差进行了处理。还对确保拓扑识别算法性能所需的线路电流传感器的数量和位置进行了可观测性分析。在33 节点测试系统和位于某地的实际运行系统中,对所提出的算法的性能进行了研究。单周期和多周期拓扑识别算法都可以识别所有可能的拓扑,包括放射型、环型和孤岛型。这扩展了拓扑识别算法的应用范围,可以识别开关故障并检测停电范围。

