基于蜂群算法和半监督极限学习机的光伏系统故障诊断
吴振庭
(中山市技师学院计算机应用系,广东 中山 528400)
复杂的室外环境导致光伏系统容易发生短路或接地等电气故障,光伏电池内部出现异常老化或热点问题,以及外部物体引起部分遮光故障等[1-2]。灰尘堆积是户外光伏系统不可避免的问题,灰尘附着在光伏组件表面会导致两种后果。首先,直接影响的是光伏发电的损耗,灰尘沉积将光伏系统的发电量减少20%,甚至80%衰减。此外,光伏组件表面不同程度积灰也会造成光伏系统相应程度的失配故障。另一方面,长期不清洁的光伏组件可能导致光伏组件下边缘出现热点和不可逆的损坏。因此,监测灰尘沉积状况,诊断污染环境下的光伏故障,是提高光伏系统可靠性的重要任务。
近年来针对各种光伏故障检测和分类方法发展了很多先进的技术。文献[3]将扩频时域反射计用于确定光伏系统的阻抗变化,以检测线路接地故障。然而,其精度容易受到光伏系统不同配置的影响。文献[4]通过降低故障光伏组件的温度水平来消除各种类型的热点,并改进了部分遮光条件下的发电。文献[5]研究了一种基于统计的方法,通过特定的检测规则检测线路和线路接地故障。文献[6]中的主成分分析和文献[7]中的小波包也被用来检测光伏系统的故障,但上述方法通常依赖于通过对故障系统的严格分析得出的手动阈值,这可能会限制监测性能和应用成效。
此外,随着人工智能技术的发展,机器学习技术得到了广泛的应用。文献[8]通过测量光伏系统的总电压和串电流,采用随机森林(Random Forest,RF)算法识别光伏故障。虽然RF 训练模型可以避免过拟合问题,但是其收敛时间随着决策树的数目而增加。文献[9]介绍了一种将阈值法与人工神经网络(Artificial Neural Network,ANN)相结合的诊断算法,用于识别六种PV 故障。然而,人工神经网络方法学习速度慢,缺乏泛化能力。文献[10]研究了一种基于I-V曲线测量的优化核极值学习机来识别PV 故障。为了利用最大功率点跟踪算法检测低辐射下的线间故障,现有文献多基于多分辨率信号分解提取故障特征,然而,基于瞬态信号的方法可能无法检测在无辐照度条件下发生的故障。文献[11]提出了一种基于I-V曲线不同点的面积和斜率的变维降维,然而该方法需要计算太多的特征来进行最优选择,并且需要为多类问题训练多个模型。文献[12]将功率比和电压比作为人工神经网络和模糊逻辑系统的输入特征,用于检测故障组件和部分阴影条件,但仅通过两个参数无法检测出异常老化或严重积尘的内部故障。此外,文献[11-12]中的检测精度容易受到PV 仿真模型的影响,并且性能受限于它们的特征归一化方法。
上述文献提出的PV 故障诊断的机器学习方法中,监督学习占主导地位。然而,监督学习往往需要大量昂贵的标记数据,这受到从实际光伏发电厂获取错误数据的困难限制。实际光伏系统运维(Opera-Tional & Maintenance,O&M)公司往往会在云中存储大量未标记的历史数据以供充分利用。而半监督学习算法可以利用这些未标记的历史数据和少量的标记数据进行分类,在光伏故障诊断中具有良好的应用前景。文献[13]提出了半监督ELM(semi-supervised ELM,SSELM)算法,与其他算法相比,具有更好的性能。然而,超参数的选取直接影响到分类精度,因此在SSELM 中训练模型的泛化能力需进一步提高。
综上,本文分析了光伏串在不同故障状态下的I-V曲线。在光伏串正常运行的情况下,利用低成本数据对I-V曲线的特征参数归一化方程进行调整。研究了一种混合人工蜂群优化和半监督极值学习机(ABC-SSELM)作为光伏串故障诊断的模式识别方法。所提光伏故障诊断技术能有效识别短路、局部遮光、异常老化、非均匀污秽和污秽条件下的故障。所提诊断模型只需要少量的标记数据,就可以利用光伏系统的历史未标记数据。此外,采用模拟故障标记样本代替实验样本,进一步节省了人工成本和时间。本文使用两个不同的光伏组件来验证模拟与实验数据,最终,通过与其他机器学习方法的比较验证了所提方法可靠性和准确性。
1 光伏串的建模与故障分析
1.1 基于MATLAB/Simulink 的PV 串建模
本节光伏系统是由13 个串联光伏组件组成的,每个组件由60 个串联单元组成,这些单元通过三个旁路二极管均匀地聚集成三个子串。MATLAB/Simulink 仿真的I-V测试电路和光伏组件如图1 所示,通过控制电压源输出值的线性增加,记录光伏串的输出电流和电压,然后将相应的数据输入MATLAB,得到最终的I-V曲线。光伏串的输出采用整流二极管,从而避免负电流的产生,辐照度和温度由每个子串的增益放大器设置。

图1 基于MATLAB/Simulink 的I-V 测试电路及光伏组件建模
1.2 光伏故障分析
本文研究的光伏串故障包括短路、异常老化、两种类型的局部遮光和不均匀沾污。STC 单一故障条件下的典型I-V曲线如图2 所示。异常老化使I-V曲线的下端变形,老化电阻可由式(1)和式(2)定义。根据在全局最大功率点跟踪点(Global Maximum Power Point tracking,GMPPT)激活阴影光伏组件内部的旁路二极管,阴影故障可分为两种类型:旁路二极管反向部分阴影(partial shading with the bypass-diode reversed,PSBR)和旁路二极管开启部分阴影(partial shading with the bypass-diode,PSBD)。在污秽情况下,灰尘附着在光伏组件的表面,从而减少了面板上的入射辐射量,这种现象对I-V曲线的电流有很大的影响。本文认为灰尘堆积是一种特殊的遮光形式。值得注意的是,光伏组件的输出电流由阴影度决定,因此,短路电流(Isc)是衡量PV 串积灰严重程度的重要指标。在实际的光伏电池串中,因为每个光伏组件都有不同程度的灰尘沉积,因此短路电流(Isc)能更具体地表示电池串中污染最小的光伏组件。

图2 STC 下单个故障典型I-V 曲线

式中:(I1,V1),(I2,V2)和(I3,V3)是离(0,Voc)最近的三个I-V点。为了抑制外部干扰和测量噪声,可以通过平均Rs的三个估计值对式(1)、式(2)进行修正。
表1 总结了STC 单一故障状态下I-V曲线的特征参数,将开路电压Voc、短路电流Isc、最大功率点电压Vm和电流Im、等效串联电阻Rs作为光伏故障诊断特征。这些不同变化的特征表现了STC 下不同故障的特征,因此,当光伏串的选定特征可以转换为STC 下的特征时,可以准确地判别光伏系统的故障类型。在STC 中,短路、PSBO 和非均匀污秽下的异常老化特性可视为单一故障状态的叠加。
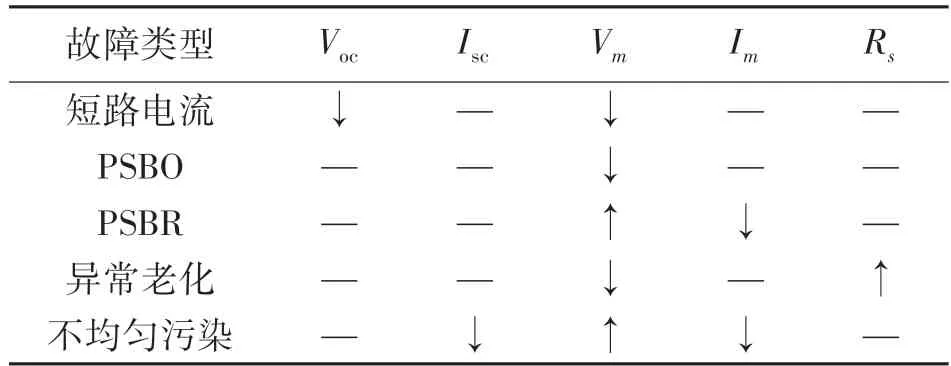
表1 STC 故障特征的变化
2 光伏系统故障诊断新技术
2.1 参数规范化
为了消除辐照度和温度对光伏系统和传感器布置的影响,本文采用文献中的特征归一化方法进行精确识别。利用光伏串在不同辐照度下的低成本正常运行数据,对输出I-V曲线特性方程的未知系数(a、b、c、d、e)进行校正,如式(3)~式(7)。将输出方程移位,除以相应的参考值,即可得到式(8)~式(12)的归一化方程。对I-V曲线的特征参数(Voc、Isc、Vm、Im、Rs)进行式(8)~式(12)归一化,可以形成一个五维诊断特征。

式中:G是测量的辐照度;Gstc是值为1 000 W/m2的常数;dT是测量的温度减去STC 温度;Voc,f、Isc.f、Vm.f、Im.f和Rs.f代表开路电压、短路电流、MPPT 点的电压和电流,并分别对不同辐照度和不同温度下的等效串联电阻进行参数拟合。Voc.stc、Isc.stc、Vm.stc、Im.stc和Rs.stc分别表示STC 下的开路电压、短路电流、MPPT 点的电压和电流以及等效串联电阻;Voc、Isc、Vm、Im和Rs分别表示开路电压、短路电流、MPPT 点的电压和电流以及等效串联电阻的测量值。
2.2 半监督极值学习机
极限学习机类似于单隐层前馈网络(Single Hidden Layer Feed Forward Network,SLFN),包括输入层、隐藏层和输出层。ELM 具有快速训练速度的能力,其结构如图3 所示。
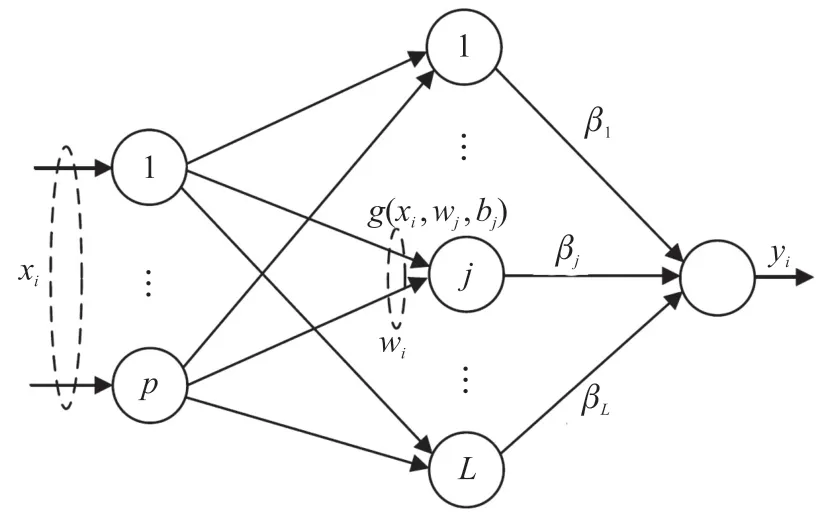
图3 ELM 网络
ELM 的关键是以最小的误差找到从输入到输出的映射空间,对于N样本(xi,yi),其中xi∈Rp,yi∈Rq,p和q代表个体维度。给定隐藏节点L和激活函数g(*),根据连续概率分布随机生成连接权重(wj)和隐藏偏差(bj)。隐藏层(H)的输出矩阵可以定义为:

ELM 网络的输出层可以表示为:
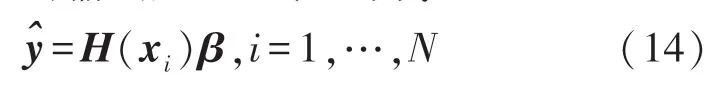
式中:β是隐藏层和输出层之间的权重,且通过以下Moore-Penrose 求逆可以得到唯一的最小范数最小二乘解:

式中:†是矩阵的Moore-Penrose 逆。
ELM 通常不太适合处理超出校准数据范围的数据。作为一种有监督的学习算法,ELM 要求大的标记样本难以获得,并且不能使用未标记样本。基于流形假设,将流形正则化框架引入到ELM 中,以改进ELM 的损失函数,形成半监督ELM(SSELM)。流形的正则化项可以表示如下:

式中:wij是xi和xj之间的成对相似度,如式(17)所示。L∈R(l+u)×(l+u)是定义如(18),其中l和u分别表示有标记和无标记训练样本的数目,本文选取了10 个最近邻图。Tr(*)表示矩阵的跟踪运算符。
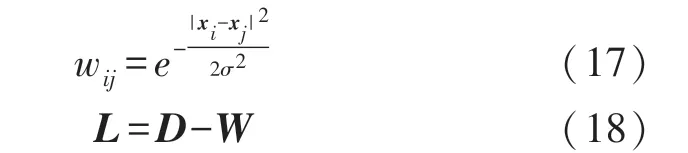
式中:矩阵D是具有以下元素的诊断矩阵:

SSELM 的目标函数定义为:

式中:λ是流形项的惩罚系数;εi是第i个标记训练样本引起的误差向量。与加权ELM 类似,Ci是针对不同类别模式的惩罚系数,用于解决不平衡数据的问题,其定义为:

式中:C0是用户定义的参数;Ni是标记为yi的训练样本数。
根据文献[13],当标记的训练数据的数目大于或等于隐藏层中的神经元数目时,可以通过下式求解:
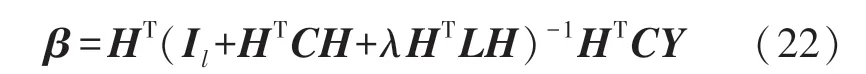
当标记训练数据的个数小于隐层神经元个数时,采用以下替代方法计算解:

SSELM 与传统的支持向量机(TSVM)和拉普拉斯支持向量机(LAPSSVM)相比的优点是能自然地处理多分类问题,其主要实现是计算H矩阵和求解输出权重β。然而,惩罚系数λ和C0的选取与SSELM 的性能有关,通常采用人工设定的经验值。此外,由于缺少有标记的验证数据集,可能导致不适定的SSELM 模型,从而出现过拟合问题。因此,采用人工蜂群算法对惩罚系数进行优化,提高了SSELM 模型的泛化能力。
2.3 混合人工蜂群算法与半监督极值学习机
人工蜂群算法(Artificial Bee Colony,ABC)是一种受蜂群觅食行为启发的群体智能算法。在控制参数较少的情况下,ABC 算法的性能优于或类似于其他基于种群的算法,如粒子群优化(Particle Swarm Optimization,PSO)和遗传算法(Genetic Algorithm,GA)。ABC 的搜索模型包括四个基本部分:食物来源、雇佣、旁观者和侦察蜂,优化的目标是寻找食物源周围的最佳花蜜。ABC 算法在SSELM 中的实现可以解释如下。
(1)初始化:本文将种群数S设为10,最大循环数(MCN)设为100。采用拟优化的SS-ELM 参数(λ和C0)的实数编码方法进行降维。

此外,ABC中每个食物源的位置可以用以下二维空间表示:
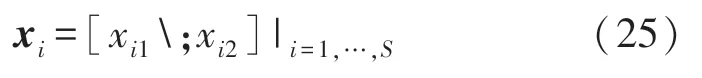
式中:S是蜜蜂种群的数量。食物源位置的上下限限制如下:
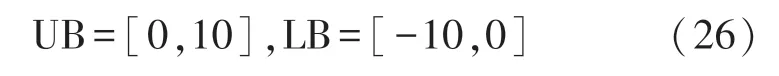
此外,初始食物来源的位置可以随机生成为:

(2)受雇蜜蜂:每种食物源xi相应地被送到一只受雇的蜜蜂寻找花蜜,如式(28)。如果发现了更好的花蜜,则食物源就更新到新位置,即更新xi为vi。否则,食物源xi仍然存在。在这项研究中,ABC的目标是寻找适应度函数的最小值,如(29)所示。

式中:φid是均匀分布在[-1,1]上的随机数;当满足条件(*)时,I(*)趋于统一和yk表示标记样本的预测和原始标记表示未标记样本的预测值表示xi的10 个邻近邻的预测。式(29)右侧的第一项是标记数据的训练错误数据,中间项表示未标记样本的聚类,这意味着具有相同结构的未标记样本属于同一类,第三项是SSELM 中输出权重的范数,系数(af和bf)是互补权重,这意味着有标记和无标记数据的重要性与其数量成反比。cf的值远小于af,bf代表了从最满足适应度函数前两项的值中找到的SSELM 模型的最佳泛化能力。
(3)旁观者蜜蜂:根据雇佣蜜蜂提供的新的食物来源信息,根据适应度值(30),发给旁观者蜜蜂以一定概率进一步探索食物来源,旁观者蜜蜂的搜索策略与雇佣蜜蜂相同(28)。

(4)侦察蜂:一些食物来源可能在几代受雇和旁观的蜜蜂之后保持不变,这可能会陷入局部最优。因此,根据式(27),侦察蜂经营者丢弃未改变的食物来源,而寻找新的食物来源。
在有足够标记数据的情况下,基于验证集的训练误差,采用ABC 算法确定最优惩罚参数λ和C0。然而,在实际的光伏系统中,故障标记数据很难获得。SSELM 的训练模型可能导致基于标记数据不足的训练误差的不适定模型。本文还考虑了未标记数据的聚类度和SSELM 的输出权重,前馈神经网络的权值范数越小,其泛化性能越好。由于ABC 的适应度函数(29)是为了优化相应的参数,并寻找SSELM 模型的最佳泛化能力,因此,可通过权衡系统性能和计算时间来选择SSELM 中隐藏的节点数。
通过ABC 法进行参数优化,得到最优的PV 故障诊断模型,所提光伏故障诊断技术如图4 所示。值得注意的是,利用正常I-V曲线的参数对规范化方程进行定期调整,可以适应光伏组件的自然老化,保持光伏故障诊断模型的长期可靠性。

图4 提出的光伏故障诊断方法的框架
本文根据光伏系统的积灰特性,分析了粉尘对光伏组件输出特性的影响,在故障识别类型中考虑了光伏系统中的非均匀污垢和非均匀污垢发生时的故障。现有文献还没有同时考虑粉尘的影响来解决光伏故障诊断问题。图4 是基于机器学习的光伏故障诊断技术的总体框架,包括数据采集、数据预处理和诊断模型建立。与其他文献相比,该方法的一个创新点是步骤4 的ABC-SSELM 半监督学习算法。该算法只需要少量的标记数据,可以利用光伏系统的历史未标记数据建立故障诊断模型。以往的研究中,有监督学习算法只能使用昂贵的标记数据来建立相应的模型。本文将参数规范化方法与模拟标号数据相结合,可以使模拟标记数据代替实际光伏系统的故障标记数据,大大降低了光伏电站信息再处理的人力和时间成本。
3 光伏诊断技术验证
如第1 节所述,正常运行和五种故障类型包括短路、旁路二极管反向部分遮光(PSBR)、旁路二极管开启部分遮光(PSBO)、异常老化和不均匀脏污。此外,本文还研究了短路、PSBO 和非均匀污秽下的异常老化等混杂故障。因此有九种光伏运行状态,包括正常运行模式和非正常运行模式,需要加以全面判别。
3.1 数据采集
两种类型的组件,包括多晶硅制造的PVM1 和单晶硅制造的PVM2,如表2 所示,用于形成两个光伏系统(3.51 kWp 和3.9 kWp),13 个组件串联,用于仿真模拟和实验验证。

表2 PVM1 和PVM2 光伏组件参数
(1)仿真数据采集
第1 节中,在不同的条件下建立了I-V测试电路,得到了相应的I-V曲线。辐照度增益放大器的值在[0.3,0.6]范围内随机选取以模拟PSBO 条件,而在[0.88,0.95]范围内随机选取以模拟PSBR 条件。作为一种特殊的阴影,各模块的辐照度增益放大器范围设为[0.7,0.9],以模拟非均匀污染情况。非正常老化故障时,老化电阻值为[3 Ω,10 Ω]。辐照度在100 W/m2到1 200 W/m2之间,温度在35 ℃到65 ℃之间同步变化。这些变化的步骤由式(31)中的确定值(A)和随机变化值(B)确定,以反映真实的环境。每9 类有600 个模拟数据样本,一个PV 串的模拟数据样本总数为5 400 个。

(2)实验数据采集
实验现场布置如图5 所示。在实验案例中,光伏系统的I-V曲线由美国TES 电子公司生产的太阳系分析仪(PROVA011)采集,光伏板的实时辐照度和温度由匹配的传感器测量。如图5 所示,短路故障是由Y 分支连接器引起的。使用小块,例如小砖块或丢弃的烟盒,来模拟PSBR 条件。使用薄塑料片或纸片来模拟PSBO 条件。

图5 实验硬件平台与故障产生机制
此外,本文亦以硬纸板作为外部物体,模拟局部阴影情况。异常老化故障采用滑动变阻器作为老化电阻,与光伏子串串联。图6 描绘了非均匀土壤及其混合断层的实验。在本研究中,以面粉模拟灰尘沉积,并在每个模组中加入50 克面粉。由于每个模块子串的输出电流受最大阴影单元的限制,一些没有足够阴影区域的单元不会影响整体输出特性,然而,这将增加由严重阴影形成热点的可能性。在这个实验装置中,人工喷雾很难确定每个子串中最严重阴影单元的相同程度,这自然会产生非均匀粉尘沉积的等效输出特性。实验环境的辐照度范围为100 W/m2~1 000 W/m2。图7 描绘了在单次故障发生,辐照度为700 W/m2时的实验I-V曲线。图7中的特性与图2 中的特性相似,PVM1 和PVM2 的测量数据总数分别为3 064 和3 013。实验中的数据选择准则是测量I-V曲线时天气稳定,也就是说,排除了在测量期间天气变化剧烈时的实验数据。

图6 非均匀腐蚀条件下的实验故障设置

图7 单故障条件下700 W/m2 辐照下的实验I-V 曲线
3.2 参数规范化
通过数值模拟和实验平台的搭建,得到了不同辐照度下光伏串的I-V曲线,以及开路电压Voc、短路电流Isc、最大功率点电压Vm和电流Im的特性参数,并提取等效串联电阻Rs作为诊断特征。此外,通过参数归一化消除了实验中的客观误差,如光伏板与被测背板之间的温差;电池与被测电池之间的辐照度不一致,以及被测设备引起的误差等。因此,在本研究中,测量值可作为参考值,盒形图是通过设置单个故障来直观地显示参数规范化的性能。以PVM1 为例,图8 描绘了归一化模拟和实验数据的统计分布,这些特征在STC 中表现出相同的聚类和统一特征。虽然实验样本受到各种环境因素的干扰而存在异常值,但其分布与仿真样本相似。该结果验证了参数规范化的有效性,为无数据情况下用仿真数据代替实测数据提供了依据。

图8 五个标准化特征变量的盒形图
3.3 所提ABC-SSELM 的性能验证
为了验证所提出的ABC-SSELM 算法对9 种PV状态的分类性能,从相应的数据集中随机获得不同数量的未标记历史数据,并且在每次训练中标记数据的数量是递增的,剩下的数据用于检验训练模型。此外,在每种情况下运行50 次,并使用平均精度来衡量所提出算法的性能。
(1)算例1:仿真验证
在这种情况下,标记和未标记的训练和测试数据是从仿真数据集创建的。PVM1 和PVM2 在不同情况下的ABC-SSELM 仿真结果如图9(a)和10(a)所示,随着标记样品数量的增加,测试精度迅速提高,“UL”表示算例中要使用的未标记数据的数量。此外,随着未标记数据的增加,训练模型的稳定性得到提高,测试精度得到进一步提高。当标记数据的个数达到总数据的0.67%时,在不同未标记数据个数情况下,平均识别率都在98%以上。结果表明,大量未标记数据可以用来提高训练模型的泛化和精度。此外,标记数据的个数占总数据个数的0.67%以上,在仿真验证中能够很好地实现对9 种光伏状态的分类。

图9 基于PVM1 的ABC-SSELM 在不同情况下的性能
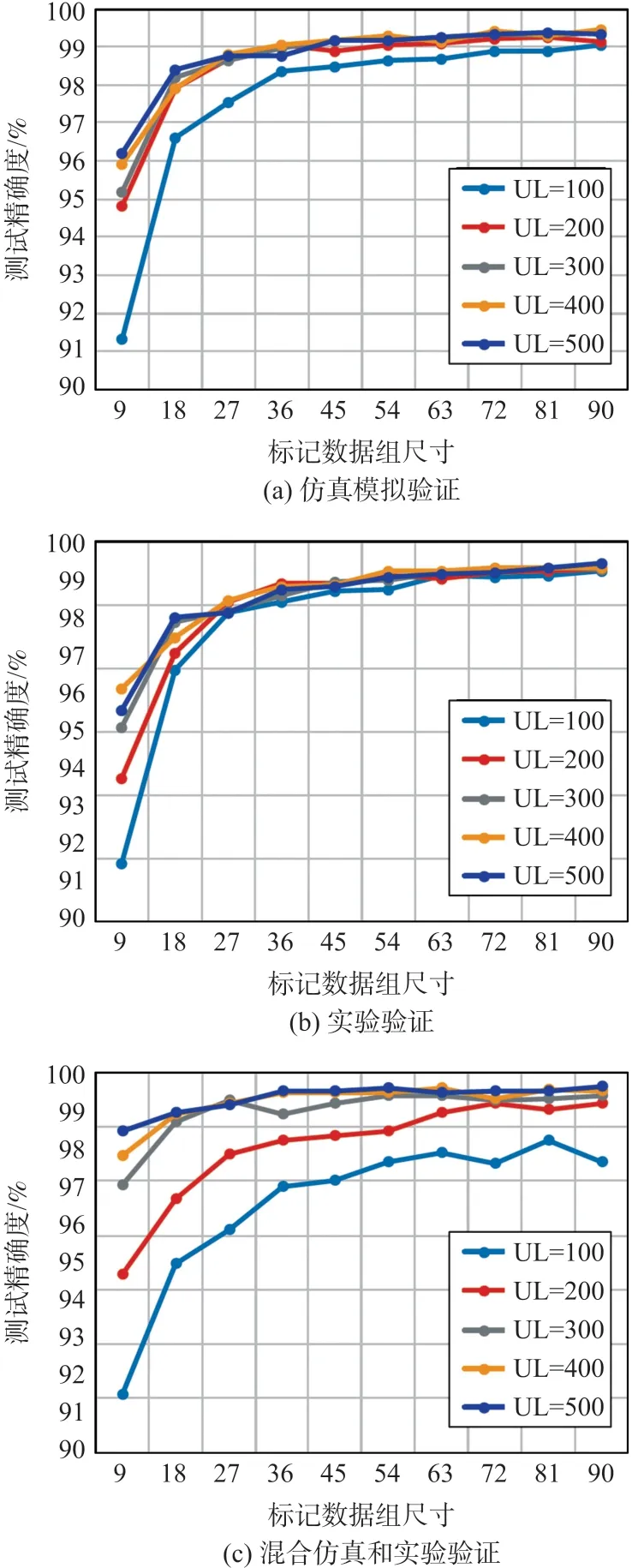
图10 基于PVM2 的ABC-SSELM 在不同情况下的性能
(2)算例2:实验验证
在实验算例中,由实验平台生成有标记和无标记的训练和测试数据。PVM1 和PVM2 在不同情况下的ABC-SSELM 仿真结果如图9(b)和10(b)所示,未标记数据和标记数据的数量对测试精度的影响与模拟数据相似。需要注意的是,与模拟数据不同,测量的实验数据中存在很多干扰因素,这将降低整体精度。然而,随着未标记样本和标记样本的增加,所提出的ABC-SSELM 仍然表现良好。当标记样本数增加到45 个(仅占总样本数的1.5%)时,PVM1 和PVM2 在所有情况下的平均准确度都高于96%。值得注意的是,少数标记数据的质量直接影响检测结果,换句话说,诊断模型会受到带有相当大噪声的标记数据的影响。
(3)算例3:混合仿真与实验验证
在这种情况下,由于光伏系统的故障数据很难获取,通常用仿真数据代替被测数据,验证相应的性能。从仿真数据集中提取有标记的样本,而将测量数据集分为无标记样本和测试样本。从图9(c)和10(c)中可以看出,未标记数据对测试精度的影响高于前两种情况,主要原因是模拟数据和实测数据的分布不同。所提出的ABC-SSELM 方法可以从未标记数据的分布中学习,提高训练模型的泛化能力,随着未标记样本的增加,实验数据的分布更加明确,训练模型的性能更加稳定,测试精度明显提高。
表3 总结了90 个标记数据和500 个未标记数据的分类结果(平均值±方差),标记数据在所有情况下占相应数据集不到总数据数的3%。需要注意的是,算例3 中PVM2 的测试精度甚至优于算例2 中的测试精度,这意味着使用模拟标记数据替换具有足够历史未标记数据的被测数据可能具有更好的性能。其原因是,被测标记数据可能带有称为离群值的大噪声,会影响模型的建立,而模拟数据在图8(a)中显示出更好的聚类效果。

表3 在不同情况下ABC-SSELM 的性能
3.4 与其他机器学习方法的比较
表1 STC 下的诊断特征是建立PV 诊断模型的必要条件,降维方法可能更适合于连续数据或高维数据,但在本文的框架中很难应用。例如,文献[6]使用了一种基于主成分分析(PCA)的多元统计方法对PV 故障进行分类,输入数据都是I-V曲线上的采样点,其数据预处理过程各不相同。本节以PVM1 为例,对ABC-SSELM 方法与其他机器学习方法进行了性能比较。在此比较中,基于参数网格搜索的原始SSELM,和基于分类和回归树(SAMMECART)的多类指数损失函数的阶段性建模,以及文中介绍的粒子群优化算法SSELM(PSO-SSELM),应用局部和全局一致性学习(LGC)算法。
图11(a)和11(b)分别描述了由监督学习(包括ELM 和SAMME-CART)进行比较的分类结果。对于算例2,在充分的数据条件下,所提出的ABC-SSELM与ELM 和SAMME-CART 具有竞争性的准确性。然而,监督学习需要大量的标记数据进行训练,对未标记数据不敏感。因此,ELM 和SAMME-CART 在算例2中没有标记数据的情况下性能较差,特别是ELM。而所提出的ABC-SSELM 保持了良好的性能。由于算例3 的训练和测试数据分布不同,即使增加训练标记,也无法改善ELM 和SAMME-CART 的性能,而所提出的ABC-SSELM 在这种情况下仍能保持很好的性能。对于图11(a)中的情况3,随着模拟标记数据的增加,所提出的ABC-SSELM 在识别测量样品方面的测试精度略有下降。当模拟标记数据的个数远大于被测数据的个数时,训练模型会明显地被模拟标记数据所支配,而从未标记数据中学习的较少。因此,在实际应用中,模拟标记数据的数量不应超过未标记历史数据的数量。

图11 ABC-SSELM 与其他机器学习方法的性能比较
图11(c)和图11(d)描述了所提出的ABCSSELM 与文献[13]中的原始SSELM 和PSO-SSELM进行比较的分类结果。原始SSELM 在没有标记数据的情况下容易产生不适定模型。此外,PSO 用于优化SSELM 中的惩罚系数,形成具有相同目标函数的PSO-SELM,与所提出的ABC-SSELM(的性能进行比较,两种群优化算法迭代次数均设置为100。从图11(d)可以看出,算例2 情况下,两种算法运行结果类似。算例3 情况下,ABC-SSELM 算法的性能比PSO-SSELM 算法要好得多,且ABC 算法比PSO算法需要确定的参数更少。
在文献[14-15]中,采用基于图形的半监督学习算法适合于诊断PV 故障,其中引用了LGC 算法。LGC 是一种标记传播算法,不需要初始训练模型就可以识别样本。文献[14]将测试数据不断地输入到LGC 中,并实时更新相应的模型,具有O(n3)的时间复杂度。为了降低算法的计算复杂度,并与ABC-SSELM 算法进行比较,文章采用300 个随机未标记数据和不同数量的标记数据,在不通过测试数据更新模型的情况下,对LGC 算法进行验证,其设置与ABC-SSELM 算法相同。从图11(e)可以看出,对于算例2 和3,所提ABC-SSELM 的分类结果都优于LGC 算法。此外,LGC 的每一个测试样本都需要重新训练模型进行预测,且耗时显著。此外,LGC的实际应用更容易受到异常值的影响,导致性能下降。显然,所提光伏故障诊断技术可以解决文献[14-15]中用模拟数据代替实测数据的问题。
以带有90 个标记数据和500 个未标记数据的PVM1 模块为例,表4 总结了不同诊断方法的计算时间比较,结果表明,本文提出的ABC-SSELM 的样本测试时间与其他基于ELM 的方法相当,比SAMME-CART 的监督学习方法和LGC 半监督方法测试时间短得多。此外,文献[14-15]中LGC 方法的测试时间会随着数据的增加而减慢,这将增加大数据的计算复杂度。而ABC-SSELM 方法结构简单,因此在线测试速度最快。

表4 不同诊断方法计算时间对比
3.4 讨论
以带有90 个标记数据和500 个未标记数据的PVM1 模块为例,在算例2 和算例3 中运行100 次。图12 给出了所提ABC-SSELM 方法中受隐藏节点数影响的平均精度。从图12 可以看出,当隐藏节点的数目增加到7 个时,平均精度可以逐渐提高。由于诊断特征的规范化和参数的优化,少量的隐藏节点即能够满足该方法的要求。因此,本研究将ABCSSELM 方法中的隐藏节点数设为7。

图12 ABC-SSELM 中隐藏节点数的影响
在第3.3 节和第3.4 节中,使用标记样本和未标记样本的动态变化来验证所提出的ABC-SSELM 方法的优越性能。图9~图11 中的每一点表示9 个光伏运行状态下的平均分类精度。以带有90 个标记数据和500 个未标记数据的PVM1 模块为例,每种情况下运行10 次,表5 总结了9 种光伏运行状态的平均精度。从表5 可以看出,所提出的ABC-SSELM 方法对9 种光伏运行状态的平均分类精度均超过98.44%。

表5 PVM1 在三种情况下的分类精度 单位:%
从以上三个算例的验证和与其他方法的比较来看,本文提出的ABC-SSELM 方法具有明显的优越性。在实际应用中,所提光伏故障诊断技术可以充分利用光伏公司存储的大量历史数据。此外,少量的标记数据可以被模拟数据代替,这进一步节省了人力和时间成本。虽然在实际应用中需要一个在线的I-V跟踪器和相关的传感器,但所提出的光伏故障诊断技术可以监测每个光伏串的运行状态,以告知潜在的故障,并带来经济效益。根据全球不同的环境,结合当地的天气预报,可以对光伏板实施有效的清洁方案。
4 结论
本文设计了一种混合人工蜂群算法和半监督极值学习机(ABC-SSELM)用于光伏发电故障诊断。其考虑了短路、旁路二极管反向部分遮光(PSBR)、旁路二极管开启部分遮光(PSBO)、异常老化和非均匀污秽五种故障类型和正常运行情况。此外,还研究了短路、PSBO 和非均匀污秽下的异常老化等混合故障。最后通过3.51 kWp 和3.9 kWp 的实际光伏串,验证了所提方法的有效性。
与有监督的机器学习不同,ABC-SSELM 算法可以充分利用未标记的历史数据,只需要总数据集中1%~3%的标记数据,同时,优化了诊断模型的泛化能力。在混合仿真和实验验证中,所提出的ABCSSELM 的平均精度比LGC 算法提高了2.94%,比SSELM 提高了1.26%,比SAMME-CART 提高了7.37%,比ELM 提高了69.28%,比PSO-SSELM 提高了0.42%。
对于所提出的光伏故障诊断技术,可以用模拟的故障数据代替难以获取的标记故障数据。在大规模光伏发电系统中,甚至可以实现更好的分类精度,避免潜在的安全问题和额外的人工成本。

