基于改进牛顿法的光伏组件5 参数模型求解算法*

张新华刘海军

(1.河南开放大学机电工程与智能制造学院，河南 郑州 450046；2.郑州大学数学与统计学院，河南 郑州 450001)

近年来，随着节能减排持续推进，绿色能源逐渐成为社会发展的重要能源之一，而光伏发电由于绿色环保，具有较强的生命周期，特别是随着光伏硅片技术的革新，光伏发电度电成本持续下降，已经基本能够实现平价上网，这也为光伏发电持续健康发展带来新的机遇[1]。无论是先前建设的集中式光伏电站，还是近年来持续推出的分布式光伏电站，特别是10 年前建设的光伏电站，由于受到环境因素，人为技术因素的影响，容易产生系统故障。持续在线监测光伏系统故障，对于提高光伏电站收益具有重要意义[2-3]。一直以来，光伏组件的数学理论模型经过国内外专家学者的持续努力，已经基本成熟[4-6]。无论是光伏组件的双二极管还是单二极管模型都涉及到5 参数的非线性方程求解的问题，国内外专家针对该问题有众多研究[7-10]。孔祥雨等人[11]依据在I-V特性方程的短路点，开路点和最大功率点得到的4 个表征5 参数之间关系的方程，采用Lambert W 函数的显式I-V方程得到光伏电池输出电流和电压。简献忠等人[12]提出了一种人工蜂群算法，该方法采用曲线拟合来求取参数，用求出的电流计算值来比较标准化的均方根误差百分比，采用变量替换法，使双二极管模型方程中指数因子只含一个变量，通过编程求解电流的计算值。师楠等人[13]详细推导了牛顿-拉夫逊和高斯-赛德尔迭代求解光伏模块输出参数的等式，利用这些等式分别对3 种不同结构的光伏模块求解参数。徐晓龙[14]从光伏电池等效电路入手推导出光伏电池数学模型并对模型进行简化，使用LabVIEW 软件建立工程数学模型。

上述研究集中于数学应用软件层面，如通过MATLAB 搭建光伏阵列模型，实现仿真，但是由于光伏组件模型的复杂性，仿真时易陷入迭代死循环，且计算速度较慢，一般而言仿真一条I-V曲线需要用时2 min 左右[15-18]，难以实现实时故障诊断。本文提出利用改进牛顿迭代算法求解简化的光伏组件5 参数模型，并搭建光伏阵列模型，将具体算法语言全部C语言代码化以嵌入下位机中，实时实现故障检测和故障诊断。试验表明，所提出的算法仿真精准度高，能够仿真出各类故障情况，且能嵌入下位机中，为光伏阵列故障检测和故障诊断提供可行性基础。

1 光伏组件5 参数模型

目前光伏电池片模型可等效为单二极管电路模型和双二极管电路模型。光伏电池片单二极管电路模型，其工作原理如图1 所示。其中Iph_cell为光生电流，与光伏电池表面辐照度大小、光伏电池本体温度相关，光伏电池表面辐照度越大，光生电流越大。Id_cell为P-N 结总扩散电流，其表达式为:

图1 光伏电池片单二极管等效电路

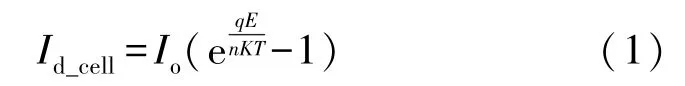
式中:q为电子电荷(1.6×10-19C)；Io为P-N 结反向饱和电流；n为二极管理想因子；K为玻尔兹曼常数(1.38×10-23J/K)。

根据图1，光伏电池片I-V特性输出方程可表示为:

式中:Rs_cell为电池片等效串联电阻，Rsh_cell为电池片等效并联电阻。

因光伏组件是由光伏电池片串并联而成，所以光伏组件I-V特性曲线可表达为:

式中:I为负载电流，U为负载电压，Iph为光伏组件等效光生电流，Io为光伏组件等效反向饱和电流，n为理想因子，Rs为光伏组件等效串联电阻，Rsh为光伏组件等效并联电阻。

短路电流指光伏组件在端电压为0 时的输出电流值，用Isc表示。其可通过式(3)求解，在式(3)中令U为0，即可得:

令Isc/Io=A，式(5)可简化为:

由于Io较小，A≫1，则Isc/A≈Isc/(A+1)。式(6)可进一步简化为:

式(7)中，Isc/(A+1)远小于其他项，可省去，式(7)可进一步简化为:

根据式(8)，A可表示为:

2 改进牛顿迭代法

牛顿迭代法又称为牛顿-拉夫逊(拉弗森)方法，它是牛顿在17 世纪提出的一种在实数域和复数域上近似求解方程的方法。牛顿迭代法是求方程根的重要方法之一，其最大优点是在方程f(x)=0 的单根附近具有平方收敛。牛顿法是求解非线性方程较为经典的方法，其表达式为:

在迭代过程中，为避免求导数，可将迭代公式改为:

考虑到牛顿迭代法具有二阶收敛性，为验证改进后的迭代算法是否具有二阶收敛性，可进一步证明如下:

设迭代误差e=xn-x0，对f(xn)在x0处泰勒展开:

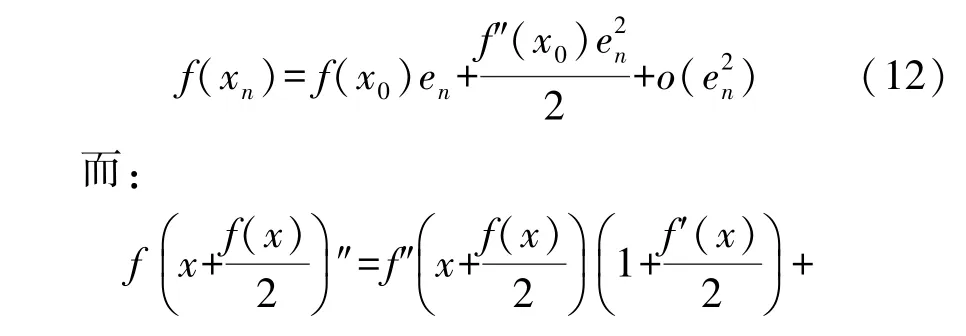
根据式(16)，可以证明该改进算法具有二阶敛散性，同时避免了牛顿迭代求解导数的问题。

3 试验验证

根据第二节，可以证明本文所提出的基于牛顿迭代的改进算法具有二阶收敛性，应用于求解光伏组件5 参数单二极管模型，具体步骤如下:

第一步:确定初始值x1，x2，其实一般可设置为x1=Isc-1，x2=Isc+1，并给定误差上限e=10-6；

第二步:将Voc进行N等分，考虑到计算精度，可在不同区间设置不同等分数量，确定N值大小；

第四步:进一步求解x1；

第五步:判断｜x1-x0｜＜e，若是x1即为所求，进行下一次迭代，此时下一次迭代初值为x1；否则继续进行迭代，以此类推。

为进一步评估光伏阵列模型性能，主要验证该仿真模型能否仿真出故障串的I-V特性曲线，分别从上述辐照区间随机各挑选一个样本，比较各辐照条件下实测最大功率与仿真最大功率的关系，如图2 所示。此外为了定量分析，利用最大功率点处的相对误差ERR 评估准确性，利用电流均方根误差RMSE 评估整条曲线的精度，具体如表1所示。

图2 典型辐照下实测与本文仿真模型I-V 曲线

表1 典型辐照下本文仿真模型与实测值比较

同时，将本方法搭建的光伏阵列模型与MATLAB光伏阵列模型进行对比，发现本文建立的阵列模型可以快速仿真各类故障条件下光伏阵列I-V曲线，如图3 所示。

图3 模拟光伏阵列I-V 曲线

4 结论

实验证明，本文所提出的光伏组件简化5 参数及相应的改进牛顿迭代算法在仿真速率、C 语言代码、仿真精度方面具有优越性，可以利用组件模型较容易地搭建任何形式的光伏阵列，并能嵌入到下位机中，实现实时光伏阵列故障仿真，可为实时进行故障诊断和故障检测创造条件。