面向风力发电系统的交直流混合升压转换器*

宋 玲

(湖北工业大学工程技术学院，湖北 武汉 430000)

风能是世界上发展最快的可再生能源之一，根据全球风能理事会的数据，2018 年全球风电总装机容量达到591 GW，其中陆上装机568 GW，海上装机23GW[1-2]。海上风力发电的成本历来高于陆上风力发电，然而，针对海上风电行业的最新报告显示，近年来，海上风电成本急剧下降，自2017 年以来，欧洲海上风电价格一直比传统电源更具有竞争力[3]。

由于风力发电机组的输出电压较低，通常采用中压变压器进行升压，然后在中压交流(medium voltage AC，MVAC)电网收集风力发电机的输出电压。然而，在50/60 Hz 频率下运行的电力变压器重量大、效率低[4]，常采用MVDC 电网结构作为替代方案，即用一个在中频(medium frequency，MF)范围内工作的中压升压功率转换器取代体积庞大的变压器。

中压功率转换器主要包括两个部分:发电机侧AC/DC 转换和升压DC/DC 电压转换。文献[5]提出了升压隔离全桥转换器的不同拓扑结构，但是需要一个中压升压变压器在中频运行。高功率水平和高匝数比下的中频变压器，在磁场中的绝缘和耦合效应方面有几个设计限制，即中频升压变压器的低压和高压绕组之间的高绝缘层要求降低了磁化电感，增加了漏感。此外，由于次级绕组匝数较多，绕组寄生电容不容忽视，为了避免使用大匝数比的中频升压变压器，文献[6] 提出了基于开关电容(switched capacitor，SC)的多单元中压转换器拓扑结构。然而，基于SC 的转换器不能在MVDC 电网上提供输出电压调节，为了调节输出电压，文献[7]提出了一种buck-boost 转换器，可以与开关电容转换器并联。

电压倍增器是一种有效的电压提升技术，可在转换器的输出级用于整流和升压交流或脉动直流输入[8]。由于电压倍增整流器(voltage multiplier rectifier，VMR)仅由不同的二极管和电容组合而成，易于实现，成本低，重量轻。全桥电压倍增器，如倍压器和四倍压器，常用于各种DC-DC 转换器[9-10]，由于电压四倍整流器可在电容器和二极管上平衡电压应力[11]，现代升压转换器中多采用了电压四倍整流器。中压升压谐振转换器可减少开关损耗，并提供升压电压转换方法[12]，然而，其在需要高电压增益时常具有高灵敏度频率控制的缺点[13]，此外，在高电压增益下，品质因数相当高，这也增加了谐振电路元件的电流和电压应力。因此，在中压升压功率转换器中使用具有很高电压增益的升压谐振电路不是一个实际的解决方案。

针对上述缺点，本文提出了一种用于海上风电系统MVDC 转换的全软开关模块化升压转换器结构，该转换器的每个模块由一个隔离谐振电路和双耦合零电流电压四倍频电路级联而成，仿真分析和样机实验证明了该结构的有效性。

1 所提转换器电路

所提出的升压型DC/DC 转换器模块化结构如图1 所示，为输入并联输出并联(input-paralleloutput-parallel，IPOP)和输入并联输出串联(inputparallel-output-series，IPOS)系统的组合。与输入串联(input-series，IS)系统相比，这种模块化配置在平衡电压和均流方面具有更好的性能[14]，且变压器二次侧模块的数量可根据所需应用和额定电压进行扩展。所提转换器的一个模块如图2 所示，由直流环节电容、开关网络、通过三绕组变压器与耦合电压四倍频器相连的CLL 谐振电路组成。

图1 模块化结构与所提转换器模块

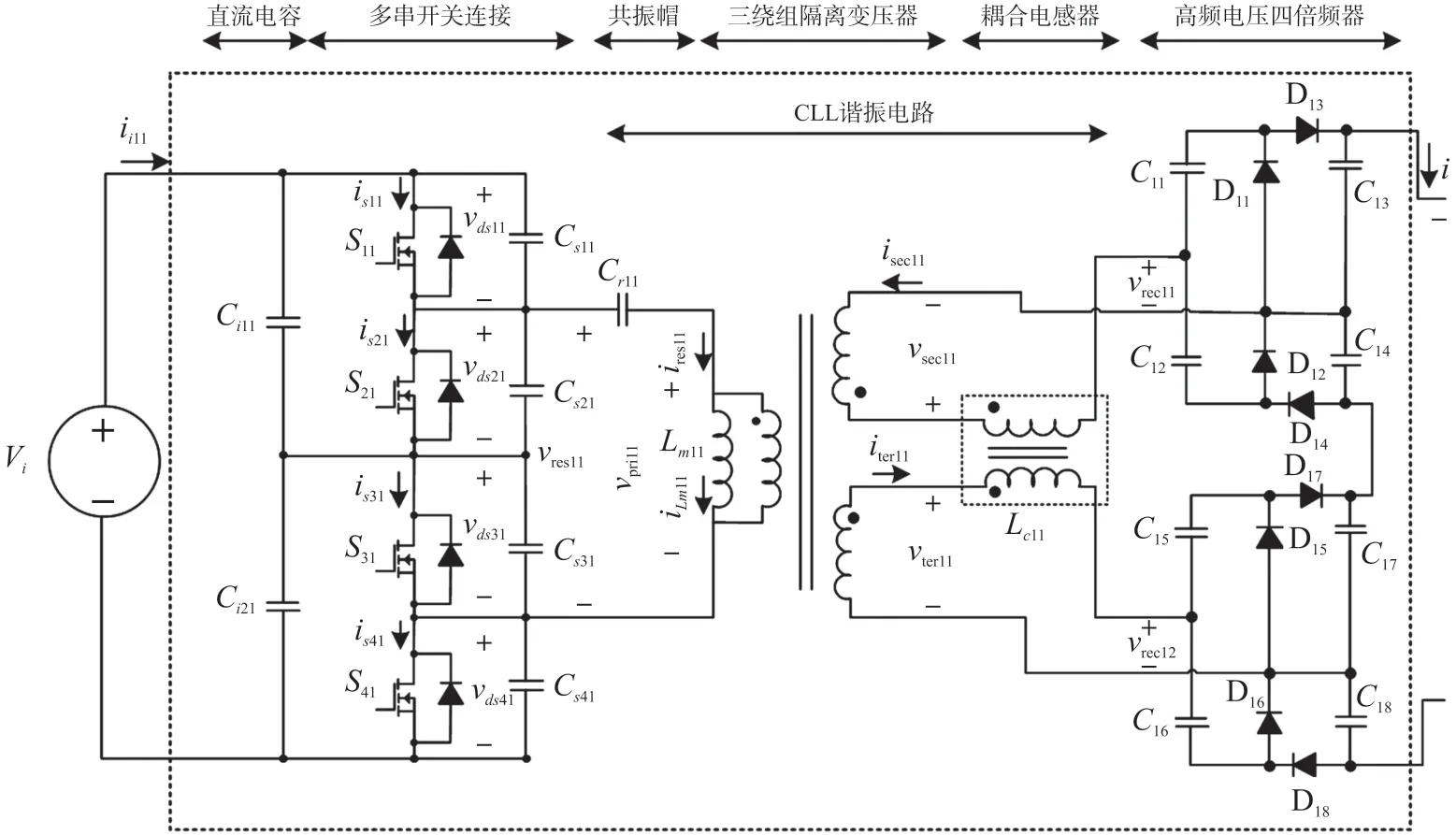
图2 基于1 ∶1 ∶1 三绕组变压器的耦合电压四倍频升压转换器的一个模块

开关网络包括“多串”开关，将每个开关上的电压应力降低到直流链路输入电压的一半。开关(S11，S41)和开关(S21，S31)以互补方式工作，开关(S11，S41)在间隔DTs期间接通，开关(S21，S31)在间隔(1-D)Ts期间接通，其中D为占空比，Ts为切换周期。隔离的CLL 谐振电路由谐振电容(Cr11)和耦合电感(Lc11)组成，耦合电感由一个单位匝数比的三绕组变压器(T11)隔离，其磁化电感为Lm11。与变压器绕组串联的谐振电容器(Cr11)也起到直流闭锁电容器的作用，以避免铁芯饱和。该转换器将变压器的非理想特性(即漏磁电感和绕组电容)纳入CLL 谐振电路的基本运行中。所有开关都可通过存储在磁化电感和耦合电感中的能量实现零电压开关导通，这些能量流过开关的反并联二极管，由于每个开关上的缓冲电容(Cs11～Cs41)随着开关的关断电压的缓慢上升而开始充电，因此可以获得接近零的关断损耗。

该转换器利用高频整流级输入端的耦合电感构成电流型高增益整流器，高增益整流器的电流驱动结构保证了二极管的平滑性能，因此，消除了二极管反向恢复损耗。通过在输出整流级对电压四倍器进行磁耦合，可以更容易地实现两个电压倍频器模块的输出直流电压平衡，而无需使用复杂的平衡控制方案[15]。此外，与单独组件的单独模块方法相比，所需磁性组件的数量也将减少，每个转换器模块的输出电压通过变频调节，如图3 所示。

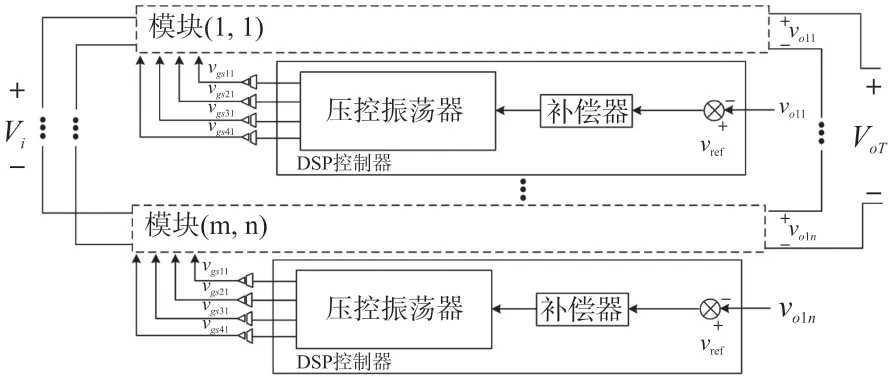
图3 所提转换器的模块化控制方案

2 转换器的工作原理

根据图4 所示的工作波形，分析该转换器的工作原理，由于两组开关(S11，S41)，(S21，S31)以互补方式控制，因此仅分析所提电路在开关周期的前半部分内的关键操作阶段，如图5 所示。

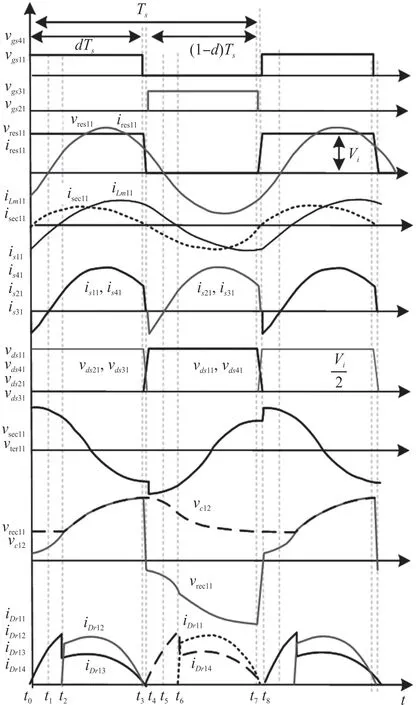
图4 模块的关键工作波形

图5 开关周期前半段内所提转换器的运行阶段

[t0＜t＜t1]:在此间隔之前，Cs11和Cs21已经放电到谐振电路，电容器上的电压已经达到零。在该阶段开始时的t0处，栅极信号被施加到S11、S41，且这些开关在零电压切换下导通。由于谐振电流ires11负的部分，电流is11(和is41)为负，通过S21和S31的电压被箝位到直流链路电容器(Ci11，Ci21)电压，是输入电压(Vi/2)的一半。在此间隔期间，变压器的二次和三次电流(isec11和iter11)开始从零上升，D13和D17传导此电流给输出电容器充电。然而，由于整流器输入电压(vrec11)小于通过C12(vc12)的电压，因此D13和D17不导通(见图4)。

[t1＜t＜t2]t1时，谐振电流(ires11)变为正值，此外，在这段时间内，变压器的磁化电流会反转极性。

[t3＜t＜t4] 在此间隔开始时，所有开关都关闭。Cs11和Cs41已经放电到谐振电路中，从而允许使用相对较大的缓冲电容器。结果，S11和S41之间的电压开始缓慢上升，并且对于S11和S41实现了接近零的关断损耗。在此间隔期间，谐振电流(ires11)等于变压器磁化电流(iLm11)，因此，isec11=iter11=0，能量不会转移到变压器二次侧和三次侧。

当栅极信号被施加到S21和S31时，该级结束，开关周期的后半部分开始。

3 变频器模块分析

图6 所示的每个模块等效电路用于完成所提拓扑的稳态分析，Rac为谐振电路输出端的等效负载电阻，磁化电感(Lm11)与耦合电感(Lc11)之比为:

图6 不同情况等效电路

随着输出功率的增加，Rac接近于低值(见图6(b))。满载时，由Cr11和等效电感Leq决定式(2)中给出的谐振频率；等效电感Leq为谐振电感和磁化电感的并联组合。

空载时Rac具有高值，如图6(c)所示。因此，谐振频率可由Cr11和Lm11定义。

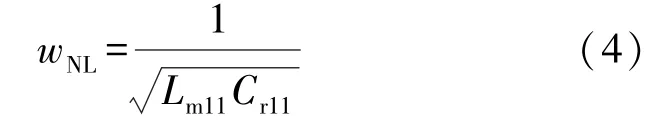
满载和空载相对角工作频率分别用ωf和ωn表示，其中，ω表示角工作频率。

式(6)中，空载时的相对工作频率ωn总是高于ωf。考虑到电路总是在高于谐振的开关频率下工作，式(6)意味着在满载时，谐振频率ωf更接近开关频率，该电路能在较宽的工作点范围内保持零电压开关，同时使导通损耗降到最小。通过采用CLL谐振电路，该拓扑结构具有串联谐振转换器满载时的固有特性，引入较少的环流。随着负载的进一步降低，该转换器利用并联谐振转换器的特性，在较宽的工作点范围内保持零电压开关。

谐振电路vres11的输入电压傅里叶级数表示如式(7)所示，其中vres11(ac)表示交流分量，由式(8)给出，D表示占空比；θh是由式(9)给出的相位角，fs为工作开关频率，h表示h次谐波。由于谐振电路中的谐波含量可以忽略不计，因此在后续计算中均使用基波近似。

3.1 逆变器谐振电流

相对角工作频率(ωr)由式(14)给出，其中ω0表示角谐振频率，Q是品质因数。

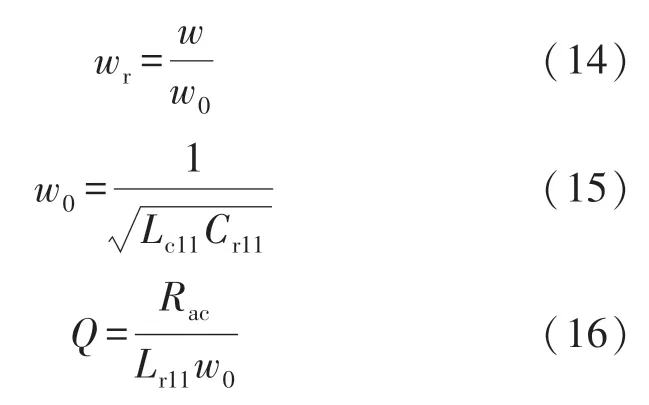
式(10)中的均方根谐振电流和基波谐振电流峰值分别由式(17)和(18)给出。Im与Ir之比由式(19)给出。式(20)表明，提高开关频率和Lm11/Lc11(k)比值，降低品质因数，可以降低电路中的循环电流，从而降低导通损耗。可以看出，随着k的增加电路可以近似为串联谐振转换器，通过并联支路(Im)的电流变为零，因此，循环电流和传导损耗将随着Lm11尺寸的增大而减小。相反，当更多电流流过并联支路时，Lm11越小，效率越低，本文目标是调整Lm11的尺寸，使ZVS 保持不变，同时使整个负载范围内的传导损耗损失最小化。

3.2 电压增益

每个CLL 谐振电路(如图6(a)所示)的电压增益及其幅值分别如式(21)和(22)所示。

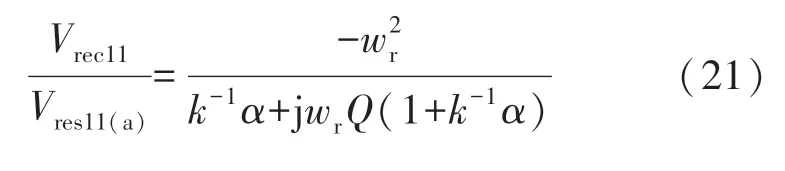
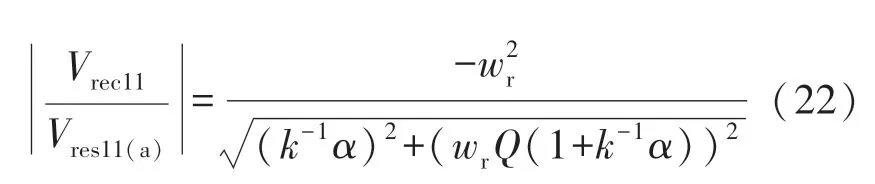
谐振电路(Cr11)的串联电容器阻断电压vres11的直流分量由式(8)可知，谐振电压vres11(ac)的均方根值如下所示:

考虑到电压四倍整流器，每个转换器模块的总电压增益如下所示:

因此，在D=0.5 时，转换器的总电压增益可由下式给出:

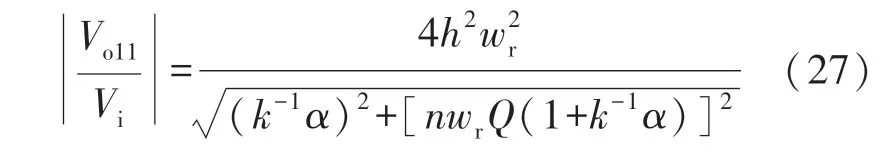
电压增益与ωr和k的关系如图7(a)所示。结果表明，每条曲线在不同的k值处达到峰值，该值为kcritical值，并表示φZi=0 的点。为实现零电压开关，工作频率应始终高于谐振频率，这意味着k值应选择在kcritical以上。从图7 还可以看出，通过降低k值可以获得更高的电压增益，另一方面，根据式(19)，降低k值可以增加循环电流。图7(b)给出了常数k(k=2)和ωr、Q的函数关系图。

图7 函数关系图

3.3 缓冲电容选择

缓冲电容器的功能是帮助实现所有开关的零关断损耗，其能量必须在死区时间内完全释放到谐振电路中。最慢的充电和放电发生在轻载和高压时，因此，缓冲电容值的上限是在轻载和高压下指定的。轻载时，假设所有电流都流经Lm11，Ceq可以通过两个缓冲电容和Cr11的串联给出。

乡村教师支持计划背景下教师生存状态省思——基于2888名乡村教师的调查分析………………张晓文 张 旭(4·80)

作为在所有条件下实现合理零电压关断的一般经验法则，场效应管缓冲电容器的充电应不小于2tfi(td＞2tfi)，其中tfi是关断时开关电流的下降时间。

此外，磁化电感Lm11必须存储足够的能量，以便对两个缓冲电容器放电:

4 硬件选择

为验证所提转换器的功能，在PSIM 中对一个输出直流电压为36 kV 的4 MW 风力发电机组系统进行了模拟。输入电压为3.3 kV，采用12 个模块，2 个串联(n=2)，3 个并联(m=3)(见图1)，每个开关上的电压应力是直流连接电压的一半。因此，采用CREE 1.7 kV、325 A 半桥SiC 场效应管模块作为4 MW模块化转换器，并给出了两个3.7 kW、500 V/2.7 kV 模块的实验结果。表1 为各模块系统规格参数。

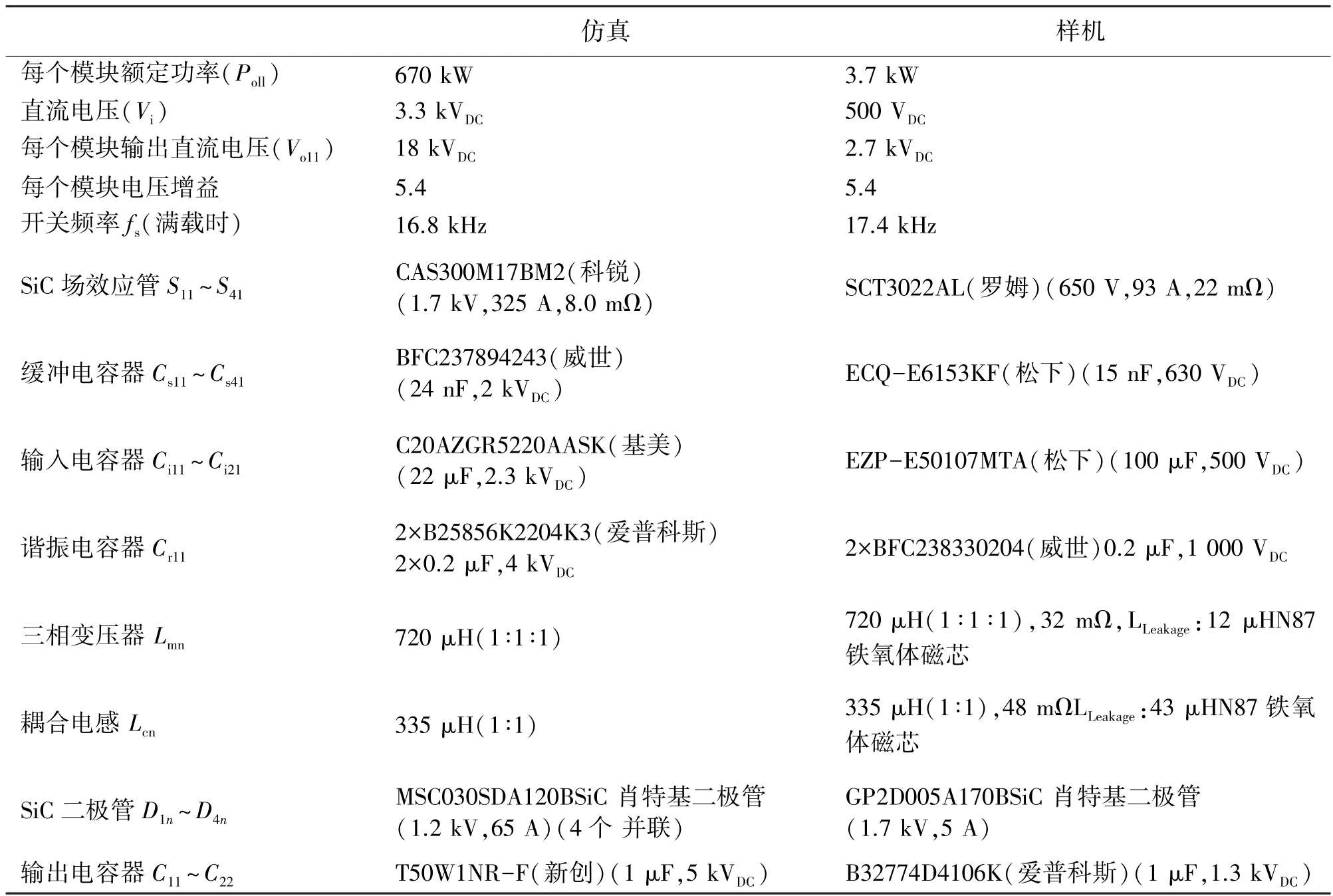
表1 用于仿真模拟和实验规模原型的规格参数

4.1 谐振槽值

等效输出交流电阻为:

假定开关频率在17 kHz 左右，为实现每个模块5.4 的电压增益，根据图7，将k和Q设置为2 和3.5，最大电压增益出现在占空比D=0.5 时。因此，根据式(27)可计算出ωr为1.2；然后，根据式(33)相应地计算出Lc11，令k=2，Lm11=692 μH，匝数比为1 ∶1，通过式(34)计算Cr11。

缓冲电容按Cs11=Cs41=24 nF 计算。

4.2 高频变压器

4.2.1 电感系数的选择

选用的锰锌铁氧体磁芯，相对温度系数αF平均值在4×10-6/K 左右，有效磁导率温度系数(αe)约为64×10-5/K，有效磁导率可由下式给出:

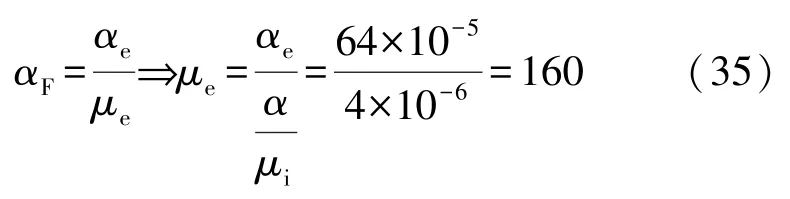
因此，当铁芯类型为PM 87/70 且μe=160 时，可从数据表中找到电感系数:AL=1 250 nH。

4.2.2 绕组材料选择

1 000 股×AWG44(即1 000×0.05 mm)天然丝包覆的Litz 线适合于高频应用，Litz 线的总截面计算为1 000×0.002 mm2=2 mm2。所选Litz 线的直流电阻为:

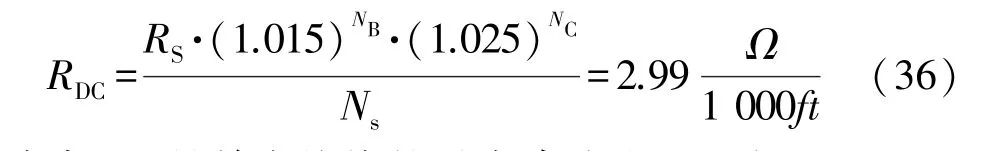
式中:Rs是单个绞线的最大直流电阻，对于AWG44为2 873 Ω/1 000ft。NB为聚束操作数，NC是布线操作数，两者都为1；Ns为单个绞线的数量。交直流电阻比由式(37)给出，其中K为常数，取决于Ns，对于Ns=1 000，K=2。D1是铜绞线上单个绞线的直径，Do是绞线上成品电缆的直径，Gin为涡流基系数。

4.2.3 匝数和电流密度

对于1 250 nH 的AL值和720 μH 的期望电感，式N=(L/AL)0.5计算得到的匝数为24，电流密度选择为4 A/mm2。变压器一次绕组的均方根电流为17 A，因此采用两根平行的Litz 线(1 000×0.05 mm)实现4.2 A/mm2的电流密度，二次绕组和三次绕组仅由一根Litz 线组成。高频变压器图片如图8所示。

图8 高频三绕组1 ∶1 ∶1 变压器图片

4.3 耦合电感器

基于上述方法设计高频变压器的耦合电感，两个铁氧体E 磁芯(65/32/27)堆叠在一起，以满足表2标准。耦合电感的结构原理和样机如图9 所示。

表2 所提转换器中使用的耦合电感的规格

图9 耦合电感的结构原理和样机图

5 仿真分析

5.1 仿真分析

图10 给出了满载条件下的仿真模拟结果，其中占空比为D=0.5，如图所示，所有开关的开关损耗均为零。通过每个开关模块的RMS 电流为212 A，电压应力为1.65 kV，这使得使用1.7 kV SiC 场效应管成为可能。图10 给出了在一个输出高频电压四倍频器模块中通过二极管的测量电流和电压波形，结果表明，所有的二极管都实现了软开关。

图10 测量电流和电压波形

5.2 实验结果

为了进一步验证所提出的拓扑结构的性能，本文在实验室中构建了两个模块，每个模块的额定功率为3.7 kW，Vi=500 V，其直流输出电压为2.7 kV，实验样机的电路元件参数与仿真结果完全相似(见表1)。由于模块的操作相同，因此只给出一个模块的结果。样机采用ROHM 公司的SiC 场效应管，高频整流级采用SiC 肖特基二极管，开关频率为17.4 kHz，占空比为D=0.5。开关波形及其导通和关断转换如图11 所示，该图表明，所提转换器可以在两组开关中保持零开关损耗。

图11 满载时模块开关波形测量值

图12 给出了输出高频电压四倍频器模块中二极管上的测量电流和电压波形。如图所示，由于SiC 肖特基二极管的软开关操作获得了平滑的转变，很明显，输出二极管上没有电压尖峰，因此，二极管的换向几乎是无损的。图12 中高频隔离变压器的二次和三次电压证明了电路的平衡性能。

图12 满载时测量的电压四倍二极管波形和高频隔离变压器的测量输出电压

在降低负载(额定功率的20%)条件下对电路进行测试，满载和20%负载条件下的测量效率分别为98.7%和95%，如图13 所示。所提出的转换器随输入电压阶跃变化的动态响应如图14 所示。可见，开关频率从Vi=500 V 时的17.4 kHz 增加到Vi=600 V 时的19.2 kHz，以保持变频控制下的输出电压在2.7 kV，采用DSP 芯片TMS320F28335 实现闭环控制，变压器的二次和三次电流随输入电压的阶跃变化如图15 所示。

图13 每个模块满载和20%负载条件下的测量效率

图14 (a)输入电压阶跃变化动态响应；(b)Vi ＝500 V时的开关波形；(c)Vi ＝600 V 时的开关波形

图15 变压器二次和三次电流在输入电压分别为500 V 和600 V 时的阶跃变化

4 MW 风电机组仿真和3.7 kW 样机中不同功率水平下的测量效率如图16 所示，图17 为电路中关键部件的热图像。温度测量表明，开关和二极管的工作温度远低于器件的最高工作温度，仿真模拟设计和样机的峰值效率分别为98.8%和98.7%。

图16 4 MW 风电机组仿真及3.7 kW 样机不同功率水平下的效率实测

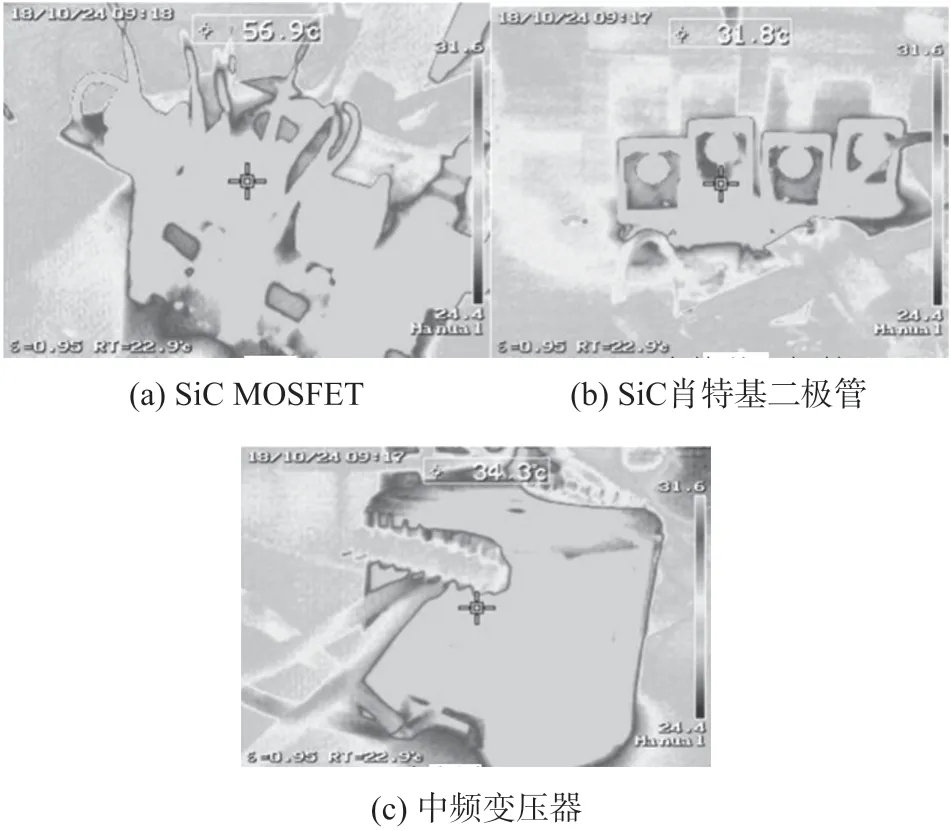
图17 样机关键部位满载热图像

图18 给出了使用MSOX6004A 示波器进行样机验证和效率测量的图片。表3 对MVDC 系统中使用的不同高升压转换器进行了比较，可以看出，所提转换器具有更好的效率性能，而开关数量较少，电压应力仅为输入直流电压(Vi)的一半。然而，与全桥逆变器产生的传统对称电压方波不同，采用调制技术时，谐振电路的输入电压为0 到Vi的单极性方波。因此，每个转换器模块中的谐振电容器还充当直流阻断电容器并行使其在谐振电路中的功能，通过谐振电容器的电压应力变得更高，例如，在500 V/2.7 kV 时，通过电容器的最大电压上升到1 kV。

表3 MVDC 电网中不同高升压变换器的比较

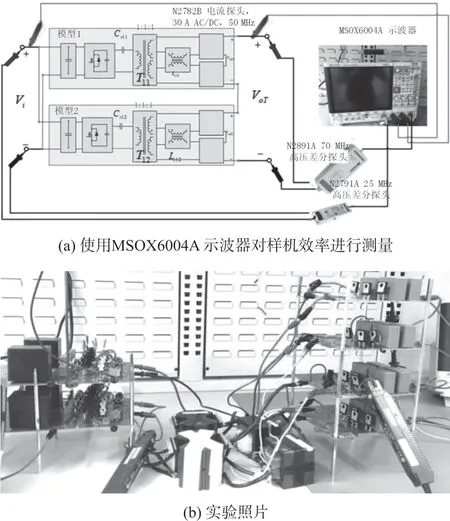
图18 样机验证和效率测量

6 结论

本文提出了一种用于风电系统MVDC 转换的混合升压电路结构，由基于耦合电压四倍频器的软开关升压谐振转换器组成，并讨论了转换器的工作原理和设计思路，在3.3 kV/18 kV(每个模块670 kW)的SiC基4 MW 模块化设计上的仿真结果和500 V/2.7 kV(每个模块3.7 kW)的实验室规模样机的实验结果，证明了所提方法的有效性。