基于有限元仿真的BGA 焊点可靠性分析*

孙勤润杨雪霞刘昭雲王 超彭银飞

(太原科技大学应用科学学院，山西 太原 030024)

球珊阵列封装(Ball Grid Array，BGA)器件由于单位空间存储量高、低电感、单位芯片面积引脚数量多等优势而被商业存储器厂商生产[1]。近年来，电子产品朝着集成化、多功能、微型化方向发展，BGA封装结构可满足客户对电子产品集成化、微型化的要求。

BGA 焊点不仅在机械电气连接、促进温度扩散、保护芯片方面起重要作用，还在器件稳定可靠性方面有重要作用。随着BGA 封装结构的广泛应用，其焊点可靠性失效问题也成为了研究的热点。电子设备在实际运行时，存在热机械疲劳、撞击和蠕变等各种负载，其中高达75%的焊点故障是由于温度和随机振动作用失效引起的[2]，而焊点塑性变形容易屈服和破坏是整个器件热失效的重要原因[3]。针对热循环和随机振动载荷下集成电路(Integrated Circuit，IC)封装因子稳健设计可靠性问题，因焊点尺寸小难试验，研究者们采用试验设计(Design of Experiment，DOE)联合有限元分析(Finite Element Analysis，FEA)方式来研究改进封装结构焊点可靠性[4]。学者谭广斌等人[5]利用L18(21×37)田口正交表，发现热作用下影响塑料球珊阵列封装(Plastic Ball Grid Array，PBGA)等效塑性应变范围较为关键因子为焊点直径和高度；熊明月等人[6]借助L9(34)田口试验表，发现影响芯片级尺寸封装(Chip Scale Package，CSP)热循环蠕变应变能密度重要因素是焊点材料和高度；韩立帅等人[7]用DOE 设计进行参数分析研究焊点随机振动载荷下焊点的应力应变分布。众多研究表明焊点直径、焊点高度、焊点间距及焊点阵列参数对焊点可靠性研究具有重要影响[8-10]。上述研究为后继者进一步研究奠定了坚实基础，但涉及焊点结构可靠性参数优化方向的研究还较少，尤其是焊点阵列参数仍需进一步的研究。

本文结合DOE 和FEA 分析技术，设计了四个包含焊点阵列、焊点径向、焊点高度和焊点间距的结构参数，研究分析BGA 器件焊点不同载荷下的可靠性，并且根据基于正交表和信噪比的田口优选法选出优化组合，进行了极差、变异性分析(Analysis of Variance，ANOVA)和交互作用分析佐证了优化结果的一致性，建立了相应三维优化模型并进行仿真计算来与原始模型做对比，验证并实现了优化。采用ANSYS 软件数值模拟出电子器件在不同载荷条件下焊点等效塑性应变和等效应力情况，分析设计了更加合理的焊点结构参数组合，以解决芯片与集成电路板之间的电气连接失效不可靠的问题。

1 BGA 焊点有限元模拟

1.1 创建模型及热循环和随机振动载荷施加

本文将选择TOPLINE 品牌的BGA 产品作为分析对象，考虑四个焊点参数对BGA 焊点可靠性进行优化设计。热作用下因结构对称性，建立1/4 模型，其能够简便且准确分析焊点应力应变响应[7]；随机振动荷载下则建立全结构模型，将BGA 结构建成PCB 板、焊点、BT 基板、Si 芯片和塑封材料五部分。具体尺寸为:焊点间距0.6 mm，焊点径向0.46 mm，焊点高度0.34 mm，焊点阵列10×10，Si 芯片6 mm×6 mm×0.28 mm，BT 基板16 mm×16 mm×0.42 mm，PCB 板20 mm×20 mm×0.57 mm，塑封材料14 mm×14 mm×0.47 mm。BGA 有限元模型见图1，焊点阵列有限元模型见图2。

图1 BGA 有限元模型

图2 焊点阵列有限元模型

根据电子封装器件的实际测试失效条件，采用了ANSYS 软件进行BGA 封装器件在热循环加速和随机振动下有限元仿真分析。有限元仿真作为以变分原理为基础的方法，可以方便划分网格，对关于热结构的复杂边界问题有很强的适应性。材料赋予PCB板、BT 基板、Si 芯片和塑料封装四部分为线弹性材料；因焊点SAC305(Sn96.5，Ag3.0，Cu0.5)熔点有217 ℃，此时表现为粘塑性应力应变，服役期间易表现为非弹性变形，且在常温下焊点的归一化温度已超过0.5，因此用粘塑性Anand 定义焊点本构关系[11]。模型结构中具体材料性能参数，见表1[7]；Anand 粘塑性本构详细参数[12]，见表2。

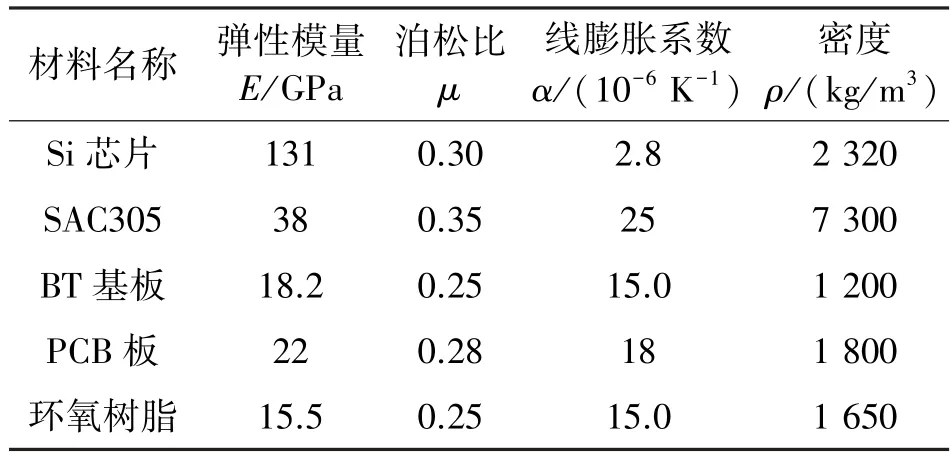
表1 材料性能参数

表2 SAC305 钎料的Anand 模型粘塑性材料参数

为了保证网格划分的精确性，对BGA 焊点进行了细致性的划分。BGA 焊点结构采用Multizone 尺寸分区控制方法进行划分。施加BGA 1/4 封装结构的热循环边界条件如下:x-z 对称面y 方向位移0 mm；y-z 对称面x 方向的位移0 mm；底面中心全方位位移为0 mm[7]。根据美军标MIL-STD-883[6]施加加速热循环交变周期载荷于整体封装结构，周围环境模拟温度为25 ℃，温度变化范围是-55 ℃～125 ℃，温度变化速率20 ℃/min，高低保温时长为15 min[6]，一个周期测试运行时间为2 880 s，运行结束后时间为11 520 s，连续施加四个加速循环周期进行仿真计算。具体施加的热循环温度载荷，见图3。

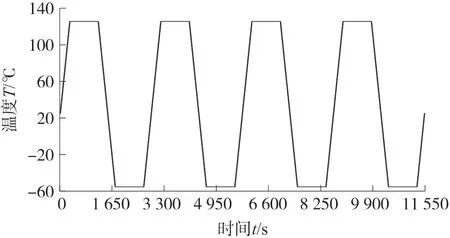
图3 热循环温度梯度载荷曲线

BGA 封装在随机振动条件下采用基于美军标MIL-ATDNAVMAT P9492 的功率谱密度(Power Spectral Density，PSD)加速度功率谱条件，随机振动加速度功率谱密度曲线，见图4。随机振动频率在20 Hz～80 Hz 时，其振动量值为+3 dB/oct，加速度功率谱密度幅值由0.01 gn2/Hz 至0.04 gn2/Hz；随机振动频率在80 Hz～350 Hz 时，加速度功率谱密度水平幅值为0.04 gn2/Hz；随机振动频率在350 Hz～2 000 Hz 时，其振动量值为-3 dB/oct，加速度功率谱密度幅值由0.04 gn2/Hz 至0.01 gn2/Hz[7]，其振动方向为垂直于PCB 板的Y 轴。

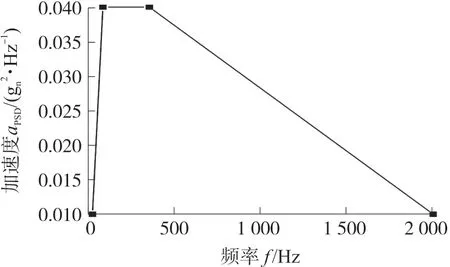
图4 随机振动功率谱密度曲线

1.2 BGA 焊点有限元结果分析

1.2.1 热循环载荷结果分析

本文BGA 焊点热失效的判据准则为基于低周疲劳的Coffin-Manson 方法[13-14]。其可通过式(1)计算:

式中:Nf为热疲劳失效寿命；Δεp为等效塑性应变范围；m为疲劳韧性指数；C为疲劳韧性系数，m、C为正常数。由此可知，无铅焊点热疲劳失效寿命与关键焊点等效塑性应变范围成反比关系，且3～4 个循环时应力应变迟滞环即保持稳定[15]，因而本文将优化目标定为第4 个周期BGA 关键焊点等效塑性应变范围。

BGA 关键焊点塑性变形发生并且伴有屈服现象，焊点界面处产生裂纹逐步扩展至其焊点材料内部，因此使得关键焊点破坏，最终导致整个封装器件失效。BGA 1/4 结构焊点等效塑性应变分布云图详情可见图5，可以看出焊点阵列经过四个稳定温度循环后，焊点等效塑性应变大小在阵列的不同区域表现不同，这是由封装结构各部分材料线膨胀系数失配，从而各部分牵扯而导致。最靠近封装中心的BGA 焊点等效塑性应变值为4.08×10-16，并且等效塑性应变范围数值有由封装中心向封装边缘扩大的趋势，在焊点阵列周围外侧和中心部分具有较大的等效塑性应变值，而最大值3.87×10-2发生在1/4 焊点阵列对角线方向上的第二个焊点上，恰好位于芯片边缘的底部，处在无铅焊点与BT 基板的交界地带，因此确定为热循环载荷的关键焊点，计算该焊点优化目标值为1.30×10-3。这是热作用加载下，各材料之间的热膨胀系数差异大，尤其芯片线膨胀系数仅为2.8×10-3K-1，比BT 基板小接近五倍，芯片硬度比基板硬度大接近十倍，而焊点作为连接器件各部分的中介，承受着较大的非弹性挤压变形所致；另外，各部分间累积的翘曲变形会加速失效裂纹的产生，且等效塑性应变在接头界面处由内向外逐层增大，而使芯片边缘的外侧焊点处为关键焊点，这与文献5 的实验及仿真研究结论相一致。

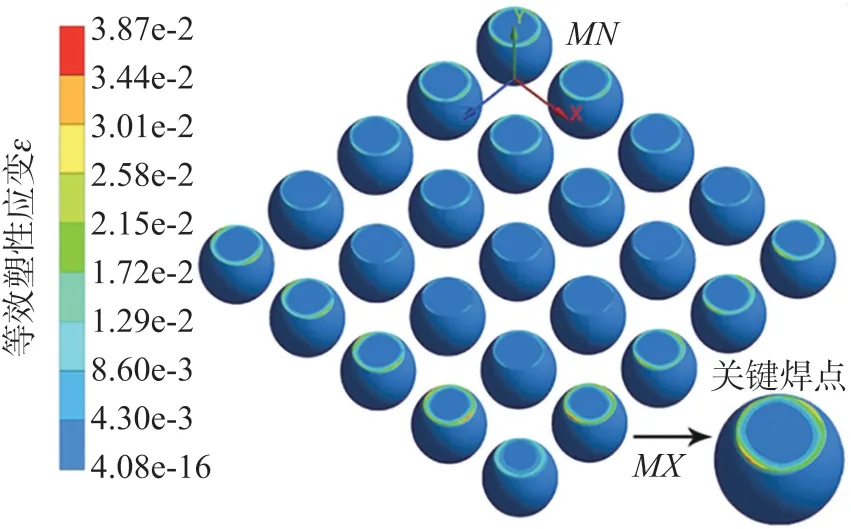
图5 BGA 1/4 结构焊点等效塑性应变云图

1.2.2 随机振动结果分析

运用ANSYS 软件进行BGA 焊点的随机振动有限元分析，建好仿真模型，施加相应材料参数后，首先对模型进行了模态分析，在PCB 板底面四个角点施加固定约束，然后再进行了PSD 谱分析，得到3D的BGA 全结构焊点等效应力云图分布情况，如图6所示。焊点等效应力值呈现四角处的焊点较高，位于中心部位的焊点等效应力较低，并且值由中心向边缘焊点逐渐增加的分布情况。最大等效应力位于距离芯片封装中心最远的焊点靠近PCB 板界面处，值为30.37 MPa。因此定该角焊点为随机振动载荷下的关键焊点，随机振动所致焊点变形四角位置比中心位置大，然后因疲劳而产生的裂纹率先在该焊点处产生，最终导致整个BGA 器件失效，这与文献[7]结果相一致。

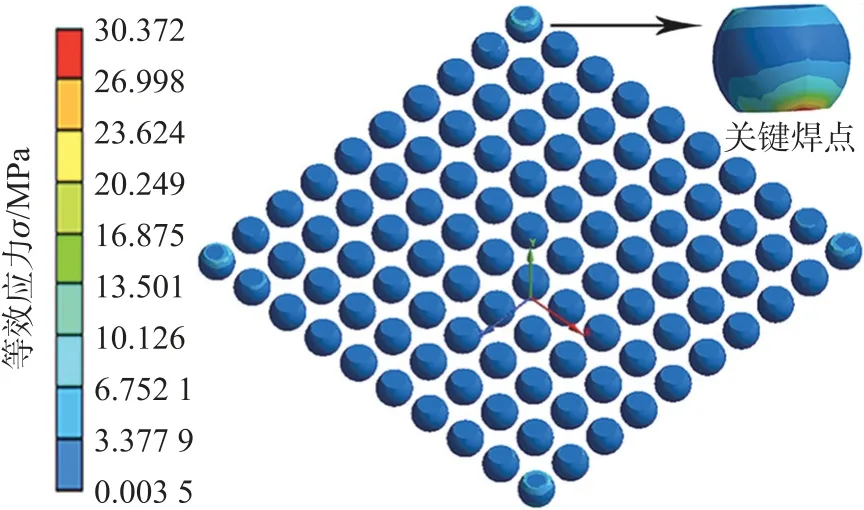
图6 BGA 全结构焊点等效应力云图

2 田口正交稳健设计

2.1 稳健方案设计原理

田口试验法利用正交表进行合理、少量、准确的试验计划，将损失函数中信噪比引入优化进程，进而判断各因素对目标函数影响程度[5，16]，最后用优化组合验证结构参数是否得到了优化。

本文采用L9(34)正交表(指由4 因素3 水平组成9 次试验)，并根据BGA 封装结构特性及焊点疲劳失效准则，将等效塑性应变范围作为优化目标，选择焊点阵列、焊点高度、焊点间距、焊点径向为控制因素，每个控制取三个水平，设计因素与水平见表3。

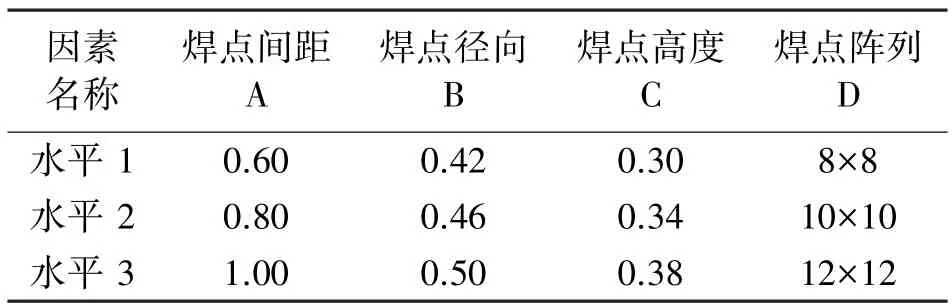
表3 控制因素及水平因子 单位:mm

2.2 信噪比极差分析

田口法评判试验组合优劣指标核心是信噪比[5-6]。其原指播音设备的功放，在此为优化目标的响应值，描述为下式(2):

式中:DS/N(Signal/Noise)指信号与噪音的比值；yi指等效塑性应变范围Δεp或等效应力σ；采用数值虚拟试验次数n=1，式(2)转化为:

按照田口正交表进行有限元分析计算，得到含有优化目标结果及信噪比响应结果见表4，将关键的极差分析信噪比均值效应绘制在图7 中。表4 中数据为随机振动相关数据，热循环载荷分析类似，不再赘述。

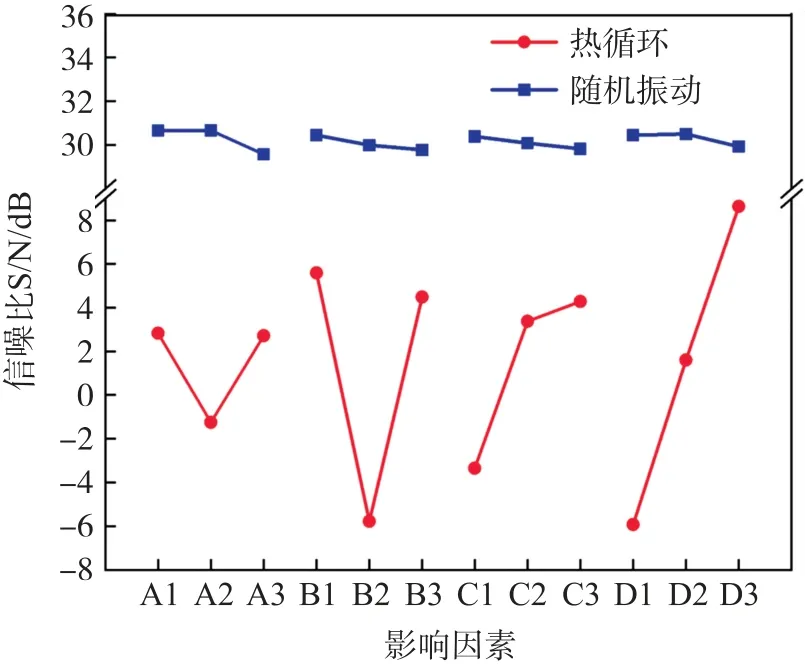
图7 不同载荷下的信噪比均值效应

表4 正交实验方案及信噪比响应

表4 中，K1、K2、K3指该因素分别在1、2、3 水平条件下，信噪比的累加和。极差R指K1、K2、K3中最大值与最小值之差，其数值大小表示的含义为组合中因子重要性的权重，数值越大表示对优化目标越有影响。因此，由表4 我们可以知晓BGA 焊点随机振动可靠性影响先后排名:焊点间距(因素A)＞焊点径向尺寸(因素B)＞焊点阵列(因素D)＞焊点高度(因素C)。优化参数配置为A2B1C1D2，即焊点间距为0.8 mm，焊点径向为0.42 mm，焊点阵列为10×10，焊点高度为0.30 mm。

同理，我们可得到BGA 焊点热可靠性影响先后排名:焊点阵列(因素D)＞焊点径向尺寸(因素B)＞焊点高度(因素C)＞焊点间距(因素A)。优化参数配置为A1B1C3D3，即焊点阵列为12×12，焊点径向尺寸为0.42 mm，焊点高度为0.38 mm，焊点间距为0.6 mm。

热循环载荷条件下，焊点阵列对热可靠性影响权重很大，可能是焊点作为芯片运行中机械的主要效用通道，焊点阵列增加焊点数量随之增加，使得每个焊点所承受的相应应力减少，而使得焊点发生非弹性变形的行为减少。随机振动载荷条件下，焊点间距为主要因素，各个因素的信噪比均值效应差距不大。

2.3 信噪比ANOVA 分析

极差分析方法只能得到各因素对试验指标影响的相对大小，利用ANOVA 分析中各因素偏差平方和分割总偏差平方和方式来相互验证显著性[17]。

以上关键计算数据均通过线性分析得到，等同于作了多重线性回归处理。得到ANOVA 分析及贡献率排名见表5，表中热循环载荷与随机振动载荷分别对应的情况是偏差平方和1、2。取BGA 焊点间距、焊点径向、焊点高度、焊点阵列四个因素对应力应变所产生影响的前两名为显著，这可以根据显著性结果有针对性地为BGA 焊点相关工艺参数可靠性设计提供依据，达到提高BGA 焊点可靠性目的。

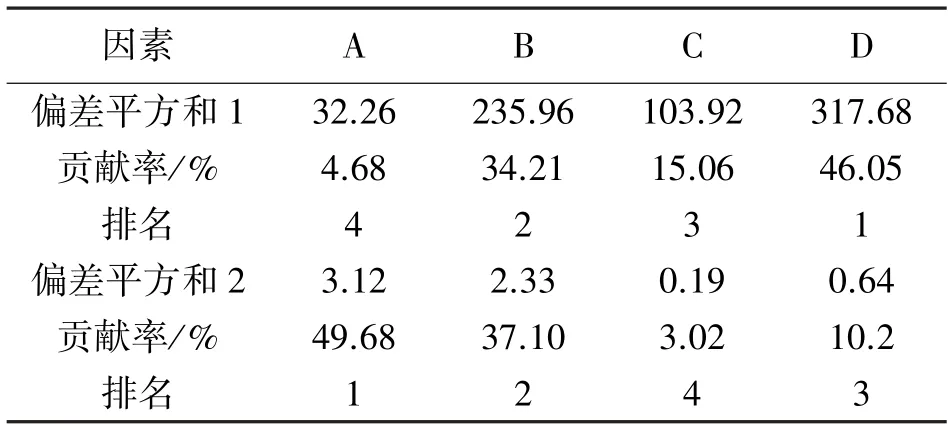
表5 ANOVA 分析及贡献率排名

据表5 可知，影响热循环权重主次顺序为焊点阵列＞焊点径向尺寸＞焊点高度＞焊点间距，且焊点阵列和径向综合贡献率比重达到了80.26%，影响非常显著，焊点阵列对BGA 焊点热可靠性影响程度最大，焊点间距影响程度最小；影响随机振动权重主次顺序为焊点间距＞焊点径向尺寸＞焊点阵列＞焊点高度，且焊点间距和径向综合贡献率比重达到了86.78%，影响也非常显著，焊点间距对BGA 焊点热可靠性影响程度最大，焊点高度影响程度最小，该排序结果的ANOVA 分析与上节极差分析排序结果相一致。

2.4 重要因素交互分析

经上节分析，由于热循环作用下因素B 和D 的综合影响权重占比达到80.26%，随机振动作用下因素A和B 的占比达86.78%，因此本节讨论了不同载荷下两组因素间交互作用对信噪比的影响，详见图8。

图8 BGA 焊点不同载荷重要因素间交互

图8 中，其条纹粗细代表两种因素组合时信噪比响应大小，且两侧同种颜色长度代表该元素的总信噪比统计值。热循环时(图8(a))，在焊点径向维持在一定水平时，总信噪比水平随着焊点阵列增加而增大，且12×12 总信噪比统计水平最高；随机振动时(图8(b))，在重要因素交互作用影响下，总信噪比水平随焊点径向减小而增加，焊点径向为0.42 mm 时总信噪比水平最高。

基于以上极差和ANOVA 分析得到的BGA 焊点热循环结构优化结果:A1B1C3D3(焊点阵列为12×12，焊点径向尺寸为0.2 mm，焊点高度为0.38 mm，焊点间距为0.6 mm)；以及BGA 焊点随机振动结构优化结果:A2B1C1D2(焊点间距为0.46 mm，焊点径向尺寸为0.42 mm，焊点阵列为10×10，焊点高度为0.30 mm)，我们再次通过FEA 模拟来验证分析比较该参数组合是否达到优化目的，详情见图9、图10。经计算表明热循环优化目标降至0.131×10-3，与原始设计比，优化目标降低了89.92%，且信噪比提高到17.72 dB；而随机振动优化目标等效应力值为24.24 MPa，与原始设计的30.37 MPa 相比，降低了20.25%，两个优化结果均比表4 中任一组都要低。实现了最初优化设计目的。

图9 等效塑性应变对比

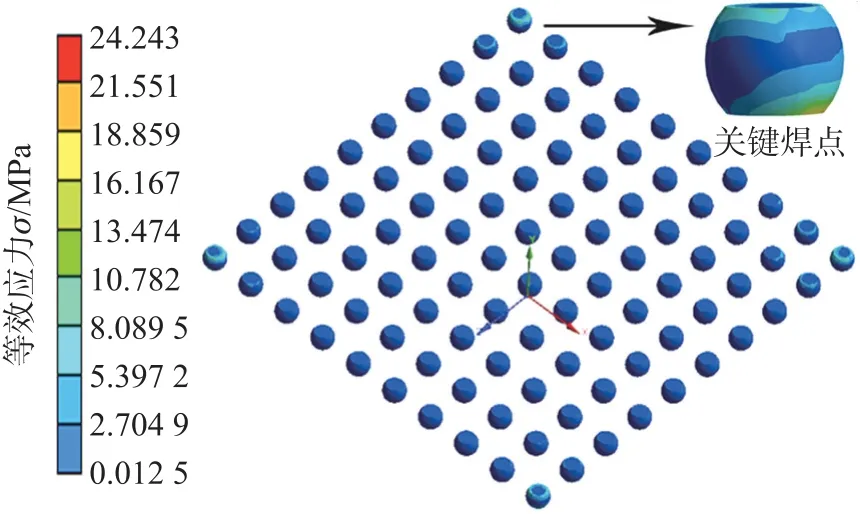
图10 随机振动优化组合等效应力云图

3 总结

针对BGA 芯片封装结构焊点力学可靠性指标不易测量的情况，本文运用有限元仿真进行了分析，并得到了两种载荷下影响封装结构失效的关键焊点位置。并运用田口法分析验证了焊点直径、焊点高度、焊点阵列、焊点间距对BGA 焊点结构可靠性的影响，并得到了一组优化设计。结果表明:热循环作用下芯片边角焊点对BGA 焊点热可靠性具有很重要的影响程度，而焊点间距对BGA 振动可靠性具有较重要影响；BGA 焊点热循环下参数优化组合焊点阵列为12×12，焊点径向尺寸为0.2 mm，焊点高度为0.38 mm，焊点间距为0.6 mm，等效塑性应变范围较初始设计降低了89.92%；随机振动下参数优化组合焊点间距为0.46 mm，焊点径向尺寸为0.42 mm，焊点阵列为10×10，焊点高度为0.30 mm，等效应力较初始设计降低了20.25%。比较系统且全面地分析了焊点结构对BGA 器件可靠性的影响，对芯片集成电路设备的安全稳定运行提供了保障。