深海多工况载荷作用下软管连接器结构强度分析1)

刘孔忠 刘统亮 何 恩 魏行超 戚 蒿 薛大智

*(中海石油（中国）有限公司海南分公司，海口 570300)

†(海洋石油工程股份有限公司，山东青岛 266520)

水下生产系统是深水油气田开发的重要模式之一，在深海环境中，水下生产系统中不同部件之间的连接主要通过水下连接器实现。采油树鹅脖连接器作为水下生产系统的重要组成部分，其上部连接水下软管，下部与水下结构物，如采油树、管汇和PLET等相连接，其结构性能的好坏直接影响到整个水下生产系统的可靠性和安全性[1]。在实际工作过程中，鹅脖连接器在船上由吊车进行提升吊装，下放至深海构建完整的水下生产系统[2-3]，复杂恶劣的海洋环境对深水采油树鹅脖连接器的结构强度提出了更高的要求。

目前，许多学者针对水下采油树连接器展开了相关研究，Shanthilal[4]提出了在高压软管接头中使用金属对金属密封，并进行了有限元模拟和现场压力测试，以检查密封件的性能。Sweeney等[5]对15 000 Psi（1 Psi=6.89 kPa）压力条件下的金属密封圈展开研究，分析了VX型金属密封圈的密封性能和挠度，获得了金属密封圈的应力应变，计算了其最小屈服强度，并通过施加不同的载荷约束来评估连接器的密封能力。李志刚等[6]在卡爪式连接器标准透镜式金属密封的基础上进行改进，研发了一种新型复合式密封圈，利用有限元软件进行不同密封角度优化，并采用内外压样机实验验证了其密封性能。程子云等[7]以一种卡箍式水下采油树节流阀连接器为例，分析了锁紧工况下的卡箍连接器强度，得到了整体的应力分布情况。曹博等[8]运用ABAQUS有限元软件，对深水连接器进行三维模型动态仿真分析，得到了内压与连接器抗弯能力和抗扭能力的趋势变化。曾威等[9]以密封强度为评价指标，分析水下采油树井口连接器密封圈密封性能随预紧力、工作压力和结构参数变化的规律。

相关研究主要集中在水下采油树井口连接器密封性能和抗拉抗弯等方面，鲜有对软管用鹅脖连接器结构强度进行分析，尤其是对其深海复杂工况进行深入研究。笔者在前人研究的基础上，以南海某气田现场使用水下采油树鹅脖连接器为研究对象，对其深海载荷工况进行计算分析，基于实验设计（design of experiments，DOE) 优化技术确定极限载荷的具体值，为最大程度地评估结构安全强度提供基础。在各工况最大载荷条件下建立有限元分析模型，对鹅脖连接器深海极限载荷工况进行模拟仿真，在此基础上根据美国机械工程师协会 (American Society of Mechanical Engineers，ASME）标准进行应力校核分析，确保整体结构强度满足安全规范要求。本文相关研究以期为工程应用中的风险预测提供参考。

1 概述

1.1 鹅脖连接器工作原理

鹅脖连接器属于连接跨接软管和水下结构物的一种立式连接器，由普通的立式连接器、弯头和提升框架组合而成，如图1左图所示。弯头一端连接立式连接器，另一端连接跨接软管，以降低软管在立式连接器上的载荷。使用此连接器既能利用立式连接器易于连接的优点，又能有效降低软管在连接器上的载荷，因此被广泛应用于深海采油树和结构物之间的连接。鹅脖连接器在深海环境进行安装时，软管首端先通过工程船上的张紧器，再和鹅脖连接器进行连接，然后进行垂直下放入水。之后通过水下机器人在海底先在软管的一端与采油树进行对接，再将软管进行平铺，软管另一端的鹅脖连接器与其他水下结构物相连。其具体安装过程示意图如图1右图所示。

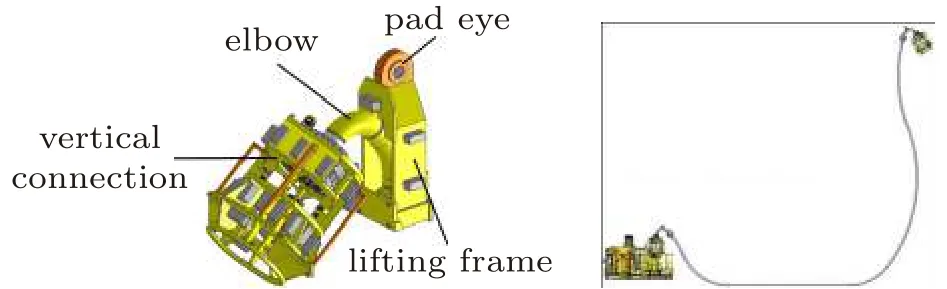
图1 鹅脖连接器及深海软管安装示意图Fig.1 Schematic diagram of the gooseneck connector and its installation with the subsea christmas tree

1.2 实例分析

以南海某气田实际使用的鹅脖连接器为例，其通过8寸生产用柔性软管一端与水下采油树相连，另一端通过软管与水下管汇连接，为生产油气的输送提供安全有力的保障。工作水深1500 m，整体自重5.1吨，连接器的母头毂座和法兰采用F65（65 K）合金钢，杨氏模量为200.35 GPa，泊松比为0.31，屈服强度为450 MPa，抗拉强度为535 MPa；弯管和90°弯头采用X65钢，杨氏模量为200.35 GPa，泊松比为0.31，屈服强度为450 MPa，抗拉强度为535 MPa。图2为现场准备安装的鹅脖连接器。

图2 南海某气田现场准备安装的鹅脖连接器Fig.2 Gooseneck connector prepared for installation at a gas field in the South China Sea

鹅脖连接器安装就位过程，主要分为三个阶段：软管平铺阶段、海底测漏阶段和静水压力测试。在此过程中，鹅脖连接器的母头与采油树上的公头进行对接并通过卡箍进行锁紧，此时在软管接头处的极限载荷将会通过鹅脖连接器上的弯管传输到母头上，然后传输到位于采油树上的连接器公头上，载荷经过传输，公头承受的载荷最小，因此，分析鹅脖连接器上母头连接处的载荷即可确定该工况下鹅脖连接器的安全性能。对鹅脖连接器的母头和法兰两处连接进行受力分析，如图3所示。

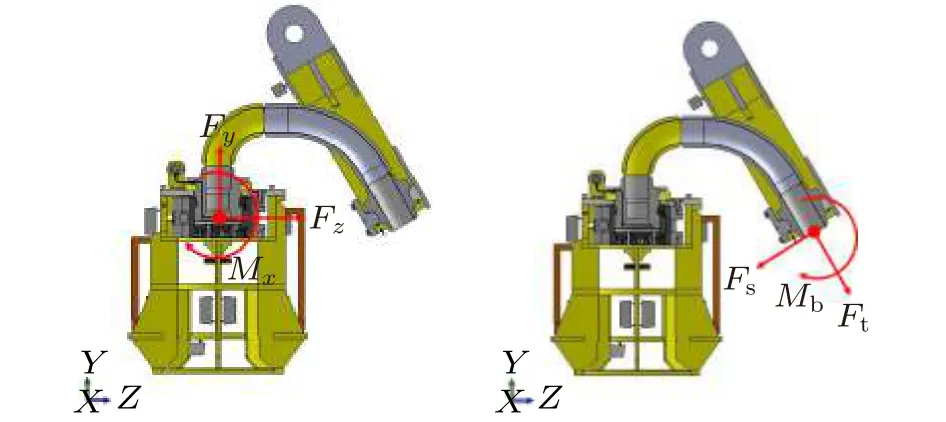
图3 鹅脖连接器承载示意图Fig.3 Bearing diagram of goose neck connector

1.3 强度评价指标

根据ASME B31.8第8章A842.22对鹅颈管进行计算分析[10-11]。

由内外压差引起的管道内环向应力Sh计算公式为

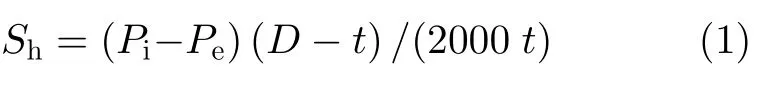
式中，D为管道公称外径，mm；Pe为外压，MPa；Pi为管内压力，MPa；t为公称壁厚，mm。

复合应力表示为von Mises应力，其计算公式为

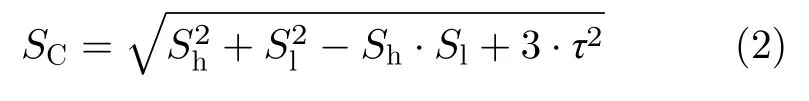
式中，Sl为最大纵向应力，MPa（正值为拉应力，负值为压应力）；τ为扭曲应力，MPa。

许用环向应力Sah计算公式为

式中，f1为环向应力设计系数，ASME查表取值0.72；S为最低屈服强度，MPa；T为温度系数，ASME查表取值1。

许用纵向应力Sal计算公式为

式中，f2为纵向应力设计系数，ASME查表取值0.80。

许用复合应力计算公式为

式中，f3为复合应力设计系数，ASME查表取值0.90。

强度评价指标为：若各应力的最大值小于相对应的许用应力，则认为强度满足要求。

2 深海载荷工况计算

DOE技术是指基于试验设计的优化技术。它根据设计点的维数以及设计变量的上下限，利用蒙特卡罗抽样技术，采集设计参数样本点，计算每个样本点的响应结果，并利用二次插值函数来拟合该多维解空间，然后根据目标函数求取该函数面的极值。作为一门工程化的科学设计方法，被广泛应用于工程实际当中[12-15]，可有效预测极值出现的位置。以最大极限载荷为目标，利用DOE技术进行系统性的载荷工况检查，并确定极限载荷的具体值，为最大程度地评估结构安全强度提供基础。

2.1 软管平铺阶段工况

在平铺过程中，首端鹅脖连接器已下放至水下采油树上，如图4所示的step 3～step 6。柔性软管在鹅脖连接器母头毂座连接处的最大载荷为：剪切力Fz= 125 kN，轴向力Fy= 150 kN，弯矩Mx= 275 kN·m。

图4 深海采油树鹅脖连接器安装过程示意图Fig.4 Schematic diagram of installation process of gooseneck connector of deepwater christmas tree

对法兰在不同承载情况进行分析，确保法兰毂面上的反作用力不会超过连接器的承载能力，同时确保鹅颈管应力处于ASME标准的应力范围内。柔性软管对鹅脖连接器法兰处施加的载荷范围为：剪切力Fs= 0～10 kN，张紧力Ft= 0～36 kN，弯矩Mb= 0～18 kN·m。采用DOE优化技术确定在该载荷范围内的最大载荷工况的具体值，建立三因素、两水平的正交试验表如表1所示，DOE试验采用全因子设计，详见表2。

表1 软管平铺阶段正交试验表Table 1 Orthogonal test table for flexible flowline laying stage

该载荷工况下各因子的正交试验表DOE矩阵如表2所示。

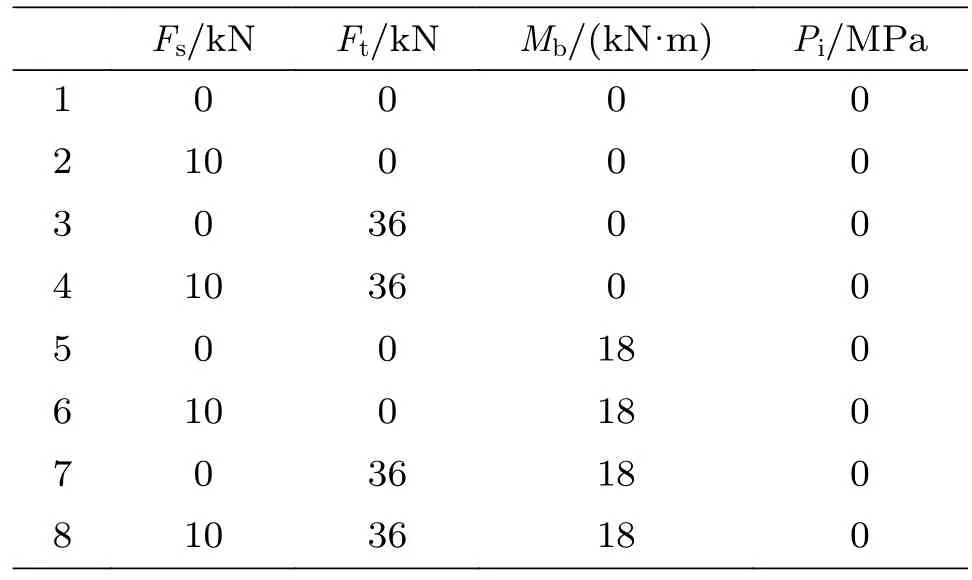
表2 软管平铺阶段DOE矩阵Table 2 DOE matrix for flexible flowline laying stage

DOE载荷矩阵计算结果如图5所示，外部连接载荷施加在法兰上，在法兰毂面上测量反作用力RF和反作用力矩RM，对于每个载荷组合，基于ASME B31.8的环向应力、纵向应力或组合应力的最大应力利用率为最大管道应力利用率。

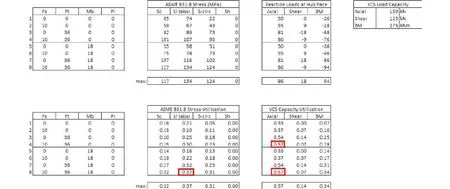
图5 软管铺设阶段法兰和毂面载荷矩阵计算和管道弯曲应力利用率Fig.5 Summary of load case check for loads at flange and hub face, pipe bend stress utilization at flexible flowline laying stage

根据DOE计算结果，对于所有载荷组合，软管平铺工况下在法兰上施加的载荷不会在法兰毂面上产生超过反作用力极限的载荷（见连接器母头承载能力），并且鹅颈管中的最高应力利用率在试验8的弯头处，低于ASME B31.8的应力极限。试验8载荷组合为张紧力Ft= 36 kN，剪切力Fs= 10 kN，弯矩Mb= 18 kN·m，软管平铺阶段在此载荷组合情况下为极限载荷工况，应力利用率最高。从完整载荷工况检查的结果可以看出，在各种不同载荷组合下，在软管平铺工况下法兰上施加的所有载荷均满足要求。下文将对试验8进行有限元分析。

2.2 海底测漏工况

在海底测漏阶段，此工况除了载荷大小与软管平铺阶段不同外，其余相似。当柔性软管首末两端鹅脖连接器均与水下结构物连接，并安装就位后，开始水下泄漏测试。根据南海某气田实际应用水深1500 m，鹅脖连接器承受水深的外部压力为12 MPa，内部压力为设计压力DP×1.1×1.05 = 43.9 MPa，内外压差为31.9 MPa。测漏过程中，鹅脖连接器在与软管连接处的法兰承受的最大载荷为：张紧力Ft= -8～40 kN，剪切力Fs= 0～25 kN，弯矩Mb= -14～61 kN·m；在连接器母头毂座连接处的最大载荷同软管平铺阶段：剪切力Fz= 125 kN，轴向力Fy= 150 kN弯矩Mx= 275 kN·m。

同理，利用DOE优化技术对海底测漏阶段进行系统性的载荷工况检查，对法兰在不同承载情况进行分析，确保法兰毂面上的反作用力不会超过连接器的承载能力，同时确保鹅颈管处于ASME标准的应力范围内。此时柔性软管对鹅脖连接器法兰处施加的载荷范围为：张紧力Ft=-8～40 kN，剪切力Fs= 0～25 kN，弯矩Mb=-14～61 kN·m。根据南海某气田实际应用水深1500 m，鹅脖连接器承受水深的外部压力为12 MPa，内部压力为设计压力DP×1.1×1.05 =43.9 MPa，内外压差为31.9 MPa，因此载荷施加等同于内压31.9 MPa和外压0 MPa。建立四因素、两水平的正交试验表如表3所示，同样采用全因子设计进行DOE试验，该载荷工况下各因子的正交试验表DOE矩阵如表4所示。

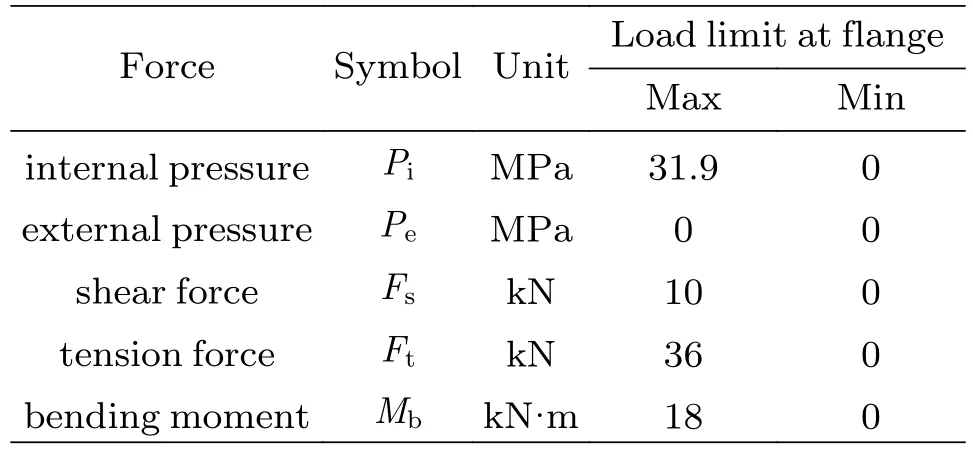
表3 海底测漏工况正交试验表Table 3 Orthogonal test table for subsea leak test

根据DOE计算结果，对于所有载荷组合，海底测漏工况下在法兰上施加的载荷不会在法兰毂面上产生超过反作用力极限的载荷，并且鹅颈管中的最高应力利用率在试验16的弯头处，低于ASME B31.8的应力极限。试验16载荷组合为张紧力Ft= 40 kN，剪切力Fs= 25 kN，弯矩Mb= 61 kN·m，软管平铺阶段在此载荷组合情况下为极限载荷工况，应力利用率最高。从完整载荷工况检查的结果图6可以看出，在各种不同载荷组合下，在软管平铺工况下法兰上施加的所有载荷均满足要求。下文将对试验16进行有限元分析。

图6 海底测漏工况下法兰和毂面载荷矩阵计算和管道弯曲应力利用率Fig.6 Summary of load case check for loads at flange and hub face, and also pipe bend stress utilization at subsea leak test

2.3 静水压力测试

在静水压力测试阶段，鹅脖连接器在海底正式投入使用之前，将对鹅颈管施加设计压力DP×1.5×1.05 = 59.85 MPa的实际静水压力进行测试。其中1.05系数是在典型FAT测试压力=设计压力DP×1.5的基础上预留额外的5%缓冲区，以考虑深海环境中可能出现的任何不确定性。

3 数值模拟结果分析及校核

3.1 有限元模型

基于上述工况和载荷条件，在ABAQUS有限元分析中，考虑到计算的收敛性，应忽略影响较小的因素。在建模时，对鹅脖的立式连接器母头和提升框架进行简化，将连接器5.1 t自重等效为在其重心位置，方便对载荷和边界条件的施加。对简化后的鹅脖连接器各部件进行建模，由于模型整体上是轴对称结构，所以采用平面轴对称方式进行建模，其有限元模型如图7所示，模型主要由灰色弯管段、红色90°弯头段、蓝色母头毂座和绿色法兰连接口四个部件组成。其各部件壁厚如下。弯管段：25.925 mm；90°弯头段：27.562 5 mm；母头毂座：31.5 mm；法兰连接处：31.5 mm。

图7 有限元模型Fig.7 Finite element analysis model

对连接器进行网格划分，整体使用C3D8I单元，该8节点六面体线性非协调模式单元，能克服剪切自锁问题，具有较高的计算精度，整体和局部加密网格如图8所示。

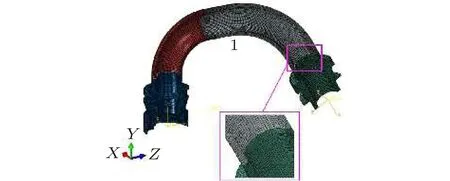
图8 有限元网格模型Fig.8 Mesh used in finite element analysis model

3.2 载荷和边界条件

基于ASME B31.8第8章对鹅脖连接器鹅颈管的载荷工况进行分析，如下。

（1）软管平铺阶段。有限元模型初始条件为：在鹅脖连接器母头毂座参考点设置1到6自由度的固定边界条件，模型整体关于X轴对称约束。根据上文工况载荷计算数据，其载荷施加步骤为：首先在鹅脖连接器重心位置施加5.1 t的重力载荷，再将柔性软管对首端鹅脖连接器的最大载荷施加在两者连接处的法兰上：张紧力Ft= 36 kN，剪切力Fs= 10 kN，弯矩Mb= 18 kN·m。该工况下鹅脖连接器鹅颈管整体载荷施加如图9所示。

图9 软管平铺阶段载荷和边界条件Fig.9 Loading and boundary conditions applied in flexible flowline laying stage in finite element analysis

（2）海底测漏工况。由上文载荷工况分析可知，除软管和鹅脖连接器法兰处所受的载荷外，鹅脖连接器还承受1 500 m水深的31.9 MPa内外压差，在载荷施加时，可等同于内压31.9 MPa和外压0 MPa。对于法兰连接端部压力的施加，考虑法兰连接处内径为210 mm，接触面积为34 636 mm2，作用在内壁上的力为内压×面积等于1140.9 kN，力的正方向与张紧力Ft的方向一致。同样有限元模型初始条件为：在鹅脖连接器母头毂座参考点设置1到6自由度的固定边界条件，模型整体关于X轴对称约束。其载荷施加步骤为：首先在鹅脖连接器重心位置施加5.1 t的重力载荷并在鹅脖连接器与软管连接处的法兰施加相应载荷：张紧力Ft= 40 kN，剪切力Fs=25 kN，弯矩Mb= -61 kNm；再对鹅颈管整体施加内压Pi= 31.9 MPa，外压Pe= 0 MPa的载荷，最后将1140.9 kN的力施加到法兰连接端部。该工况下鹅脖连接器鹅颈管整体载荷施加如图10所示。

图10 海底测漏阶段载荷和边界条件Fig.10 Loading and boundary conditions applied in subsea leak test in finite element analysis

（3）静水压力测试。由2.3节分析可知，FAT测试压力=设计压力×1.5×1.05 = 59.85 MPa，计算方法同上文，法兰连接端部施加的力F=59.85 MPa×34 636 mm2=2073 kN。有限元模型初始条件为：在鹅脖连接器母头毂座参考点设置1到6自由度的固定边界条件，模型整体关于X轴对称约束。其载荷施加步骤为：首先在鹅脖连接器重心位置施加5.1 t的重力载荷，再对鹅颈管整体施加内压Pi= 59.85 MPa的载荷，最后对法兰连接端部施加2073 kN的力。该工况下鹅脖连接器鹅颈管整体载荷施加如图11所示。

图11 静水压力测试载荷和边界条件Fig.11 Loading and boundary conditions applied in hydrostatic pressure test in finite element analysis

3.3 数值模拟结果分析及校核

根据ASME B31.8第8章对上述工况载荷进行有限元计算，其应力分布云图和有限元强度计算结果如下所示。

（1）由1.3节强度计算可知，环向应力Sh是仅由压力载荷引起的周向应力，对于软管铺设阶段，无压力载荷，因此环向应力Sh=0 。

从图12和表5可知，在软管平铺阶段，连接器毂面载荷能力在反作用载荷范围内，鹅颈管整体应力均小于ASME B31.8应力极限值，表明在此工况下鹅脖连接器结构综合强度足够，整体结构强度满足ASME规范要求。

表5 软管平铺阶段ASME B31.8应力使用率Table 5 ASME B31.8 stress utilization at flexible flowline laying stage

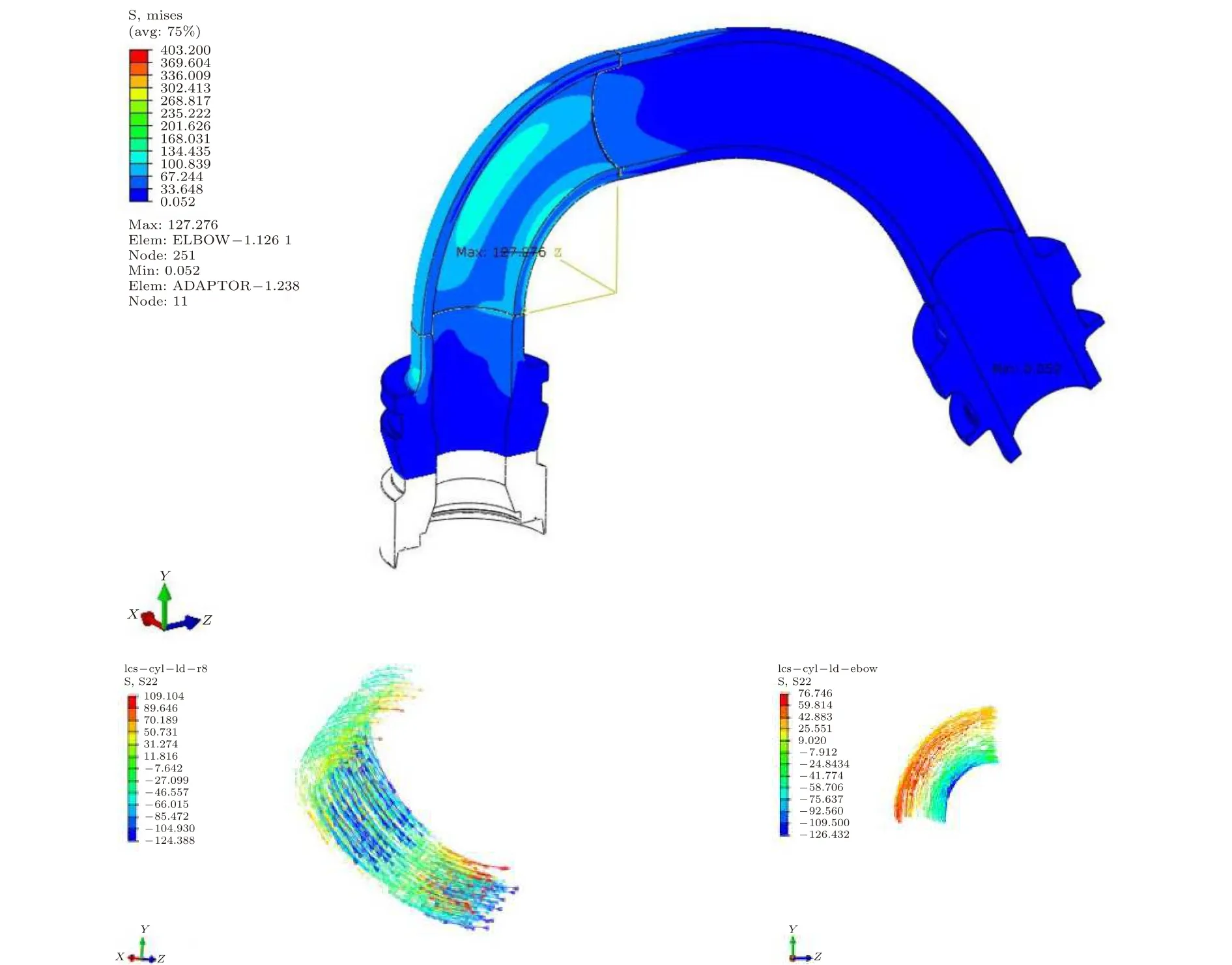
图12 软管平铺阶段鹅颈管应力分布Fig.12 Stresses on the gooseneck pipe at flexible flowline laying stage

（2）对海底测漏工况下内外压差以及承受载荷条件下的鹅脖连接器鹅颈管模型进行计算，应力分布云图如图13所示，该工况下有限元强度计算结果见表6。

表6 海底测漏阶段ASME B31.8应力使用率Table 6 ASME B31.8 stress utilization at subsea leak test

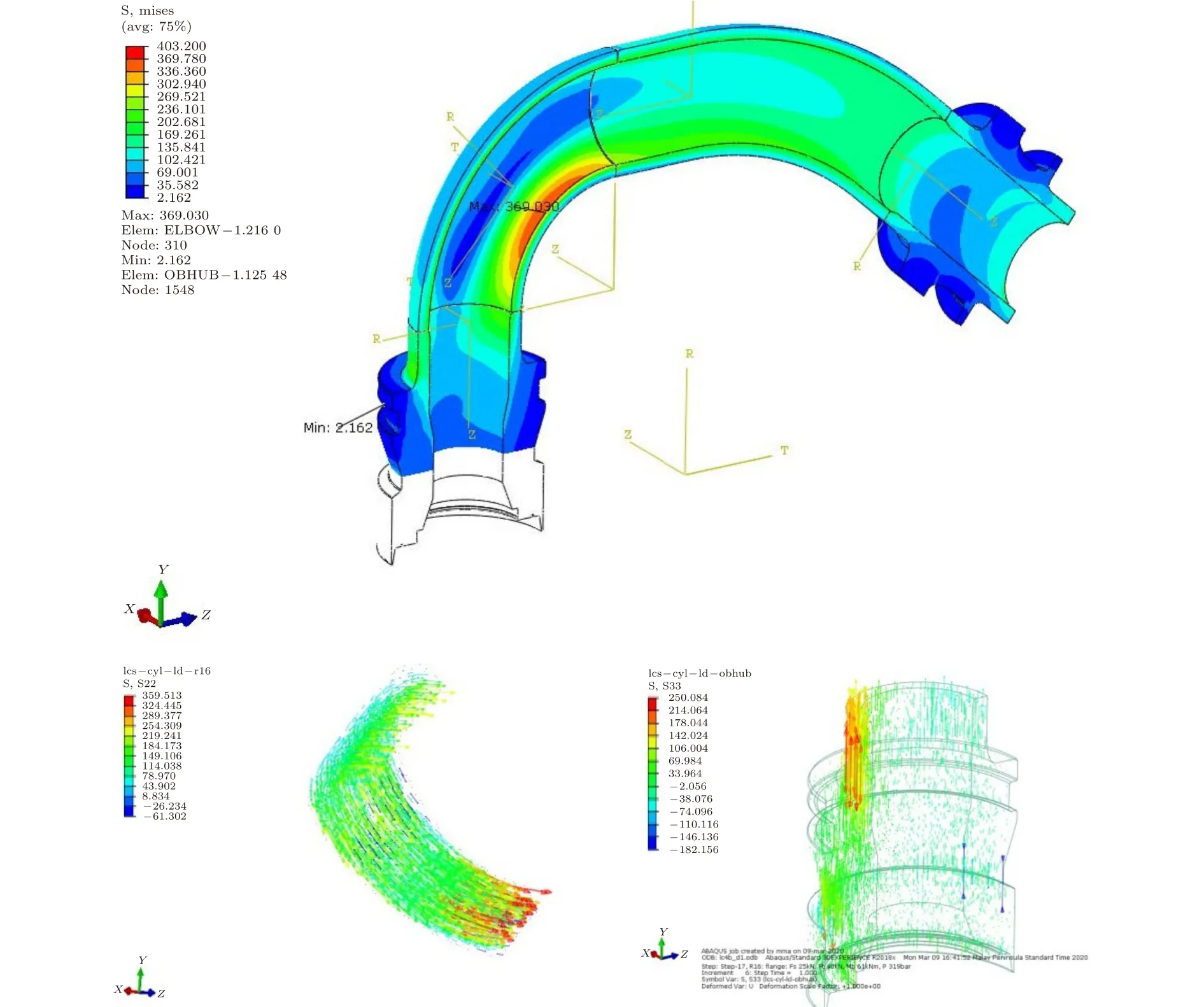
图13 海底测漏工况鹅颈管应力分布Fig.13 Stresses on the gooseneck pipe at subsea leak test

根据上文分析，从ASME B31.8标准可知：Sh=(Pi-Pe)(D-t)/(2000t)= 152.0 MPa。为了在环向应力计算中更为保守，上式中的“t”值使用的是壁厚减去公差，而非标准壁厚。

从图13和表6可知，在海底测漏阶段，连接器毂面载荷能力在反作用载荷范围内，鹅颈管整体应力均小于ASME B31.8应力极限值，表明在此工况下鹅脖连接器结构综合强度足够，整体结构强度满足ASME规范要求。

（3）静水压力测试

对静水压力测试工况下施加内压以及承受载荷条件下的鹅脖连接器鹅颈管模型进行计算，应力分布云图如图14所示，该工况下有限元强度计算结果见表7。

此时环向应力Sh=(Pi-Pe)(D-t)/(2000t) =285.2 MPa，同样，为了在环向应力计算中更为保守，上式中的“t”值使用的是壁厚减去公差，而非标准壁厚。

从图14和表7可知，在静水压力测试阶段，出厂验收试验测试压力FAT= 59.85 MPa载荷工况下，鹅颈管整体应力均小于ASME B31.8应力极限值，表明在此工况下鹅脖连接器结构综合强度足够，整体结构强度满足ASME规范要求。

表7 静水压力测试阶段ASME B31.8应力使用率Table 7 ASME B31.8 stress utilization at hydrostatic pressure test

4 结论

（1）深海多工况载荷对软管连接器的结构安全性能提出了更高的要求，以南海某气田软管鹅脖连接器深海安装工程为例，基于ASME相关标准，利用DOE优化技术开展多工况极限载荷计算，并利用有限元数值模拟对软管连接器进行安全强度校核。

（2）针对深海多工况载荷施加复杂问题，利用DOE优化技术建立试验矩阵，在软管平铺阶段、连接器测漏和静水压测试三种深海工况对鹅脖连接器进行了极限载荷分析计算，得到各工况条件下最大载荷的具体值，最大程度上减少计算工作量。

（3）数值模拟结果表明：在各种不同载荷组合下对鹅脖连接器进行完整载荷工况检查，各工况条件下法兰上施加的所有载荷均满足要求；鹅脖连接器在各工况下整体应力均小于许用应力，整体结构综合强度足够，满足安全规范；各工况最大应力均集中在90°弯头处，对其进行强度校核，满足ASME标准使用要求。本文分析结果可为水下软管连接器的结构优化设计和深海安装提供理论基础和技术参考。