g-ZnO 基异质结电子结构及光催化性能的第一性原理研究
潘多桥 ,赵旭才 ,雷博程 ,黄以能, ,张丽丽,
(1.伊犁师范大学 物理科学与技术学院 新疆凝聚态相变与微结构实验室,新疆 伊宁 835000;2.南京大学 物理学院 固体微结构物理国家重点实验室,江苏 南京 210093)
太阳能为一种清洁、可持续发展的新能源,利用太阳能解决全球的能源及环境问题具有重要意义[1-2]。而寻找一种可以直接利用太阳能进行光催化反应的半导体材料也引起研究者们的关注。2004 年Novaselov等[3]成功制备了具有优异性能的单层石墨烯,但石墨烯是零带隙半导体[4],在光催化领域的实际应用中受到限制,因此研究具有类石墨烯结构的二维光催化材料尤为重要。同年Claeyssens 等[5]理论预测了类石墨烯ZnO(g-ZnO)可以稳定存在,随后在2007 年Tusche等[6]成功验证了随着g-ZnO 的层数减少,其结构从纤锌矿转变为类石墨烯结构,并且可以稳定存在,自此受到研究者们的青睐。g-ZnO 是直接带隙半导体材料,其禁带宽度为3.370 eV[7],由于宽带隙和电子空穴对复合的原因,g-ZnO 对可见光的利用率较低[8-9],因此提高g-ZnO 对可见光的利用率就要解决宽带隙和电子空穴对复合两个问题。迄今为止,研究人员为解决该问题对其进行了多种改性方法,如: 元素掺杂[10]、应变调控[11]、异质结工程[12-13]等,其中异质结工程会引起材料应变[14],抑制电子空穴对复合[15-16],已被证明是提高光催化能力的一种有效方法。如MoS2/WS2异质结[17]、GaSe/g -C3N4异 质结[18]、C2N/MoS2异质结[19]等都实现了电子与空穴的分离,且提高了半导体的光催化性。以上研究表明搭建异质结是一种有效控制电荷分离且提高光催化效率的方法。
目前关于ZnO 为基底的异质结光催化性能研究已取得重要进展,如通过对g-ZnO/CuO 异质结[20]和C/ZnO 异质结[21]研究发现,相对ZnO,异质结的带隙减小,光吸收带边扩展至可见光区域(2.8 eV),有效提高了ZnO 对可见光的利用率;与此同时,还有研究者对g -ZnO/TiS2[13]、g -C3N4/g -ZnO[22]、SnO2/g -ZnO[23]、g-ZnO/ZnS/CdS[24]等异质结进行研究,发现g-ZnO 基异质结可以有效抑制电子和空穴的复合,同时具有优异的光催化性能。由此表明构建g-ZnO 异质结是提高g-ZnO 对可见光利用率的有效方法。
基于以上调研,为避免晶格失配率过大导致无法形成稳定的异质结,故选择与g-ZnO 同为一种空间群(P63MC)的半导体,如: GaN[25-26]、SiC[27-28]、WS2[29-30]、BN[31]、GaSe[32]、PtO2[33]等,其中GaN、SiC、WS2均为类石墨烯结构的二维半导体材料,具有带隙可调、高比表面积和耐高温等优异的物理化学性质[29,34-35],是良好的光催化剂。同时研究g-ZnO/X(X=GaN,SiC,WS2)异质结的界面电荷转移及光学性质对g-ZnO 在光催化领域中的应用具有重要意义。
为此,本文选择用单层g-ZnO 为基底搭建g-ZnO/X 异质结,通过第一性原理方法对其电子结构、界面电荷转移及光吸收等性质进行深入研究,期望能够为g-ZnO 基异质结实验上的制备研究提供理论参考。
1 计算方法及模型
本实验的计算工作基于密度泛函理论(DFT)第一性原理方法,利用 Materials studio 2017 中的CASTEP[36-37]软件完成计算,采用广义梯度近似(GGA)的Perdew-Burke-Ernzerhof(PBE)[38]泛函描述电子交换和关联作用;并采用GGA+U[39](UZn:3d=8.120 eV,UO:2p=4.640 eV)得到g-ZnO 禁带宽度为3.270 eV,与实验值(3.250 eV)[22]吻合很好。考虑到DFT 处理范德瓦尔斯相互作用(vdw)存在一定范围的误差,因此选择DFT-2 中的Tkatchenko-Scheffler(TS)[40]进行修正。为满足原子周期性排列和避免边界效应的影响,通过文献调研[41-44]和计算不同大小超胞(1×1,2×2,3×3,4×4)的结合能,如图1 所示,发现当超胞大小为3×3,4×4 时,结合能趋于平稳,说明结构达到稳定状态。因此选择构建3×3 的g-ZnO 和g-ZnO/X 异质结超胞进行性质计算,其结构如图2 所示。根据Monkhorst-Pack 方法[45-46]结合文献调研和收敛性测试,对g-ZnO、g-ZnO/X 异质结采用7×7×3的k格点进行几何优化,其截断能为550 eV。晶体优化收敛标准: 最大位移2×10-4nm,内应力收敛标准0.1 GPa,SCF 收敛标准为2.0×10-6eV/atom,能量收敛标准为2.0×10-5eV/atom。为避免相邻单层结构之间的相互作用,在c轴建立2 nm 的真空层。

图2 结构图。(a) g-ZnO,俯视;(b) g-ZnO/GaN 异质结,侧视;(c) g-ZnO/SiC 异质结,侧视;(d) g-ZnO/WS2异质结,侧视Fig.2 Structure diagram.(a) g-ZnO,top view;(b) g-ZnO/GaN,side view;(c) g-ZnO/SiC,side view;(d) g-ZnO/WS2,side view
2 结果与讨论
2.1 晶体结构稳定性分析
为构建合理的g-ZnO/X 异质结,首先对单层的g-ZnO、GaN、SiC、WS2进行几何优化,进一步研究g-ZnO/X 三种异质结的晶格匹配情况,并计算三种异质结的晶格失配率,其公式为[47]:

式中:a1、a2分别表示几何优化后的晶格常数,几何优化后g-ZnO、GaN、SiC、WS2的晶格常数如表1所示,其晶格失配率分别为1.3%,4.9%,2.6%,均小于5%,说明两种半导体之间可以较好地匹配。但由于半导体之间晶格失配的原因,会引起界面处产生晶体结构畸变,因此以能量为收敛标准对三种异质结进行优化,优化后异质结的层间距分别为0.3576,0.4008,0.3505 nm,其范德瓦尔斯力与之前报道的数值接近[48-49],表明构建的三种异质结接触方式均为vdw 接触,这将保留异质结中单个组分的结构特征。
为了选择更稳定、更合理的异质结,计算得到异质结的结合能[50]:

式中:Eg-ZnO/X,Eg-ZnO,EX分别是g-ZnO/X 异质结、g-ZnO、单层GaN、SiC、WS2的总能量,若异质结的结合能为正值,表示异质结在形成过程中为吸热反应,其稳定性不佳,不利于实验制备;结合能为负值,其形成过程为放热反应,稳定性良好,在实验上可以制备获得。根据表1 可知,g-ZnO/SiC 和g-ZnO/WS2两种异质结结合能为负值,表明在实验中更容易形成这两种异质结。
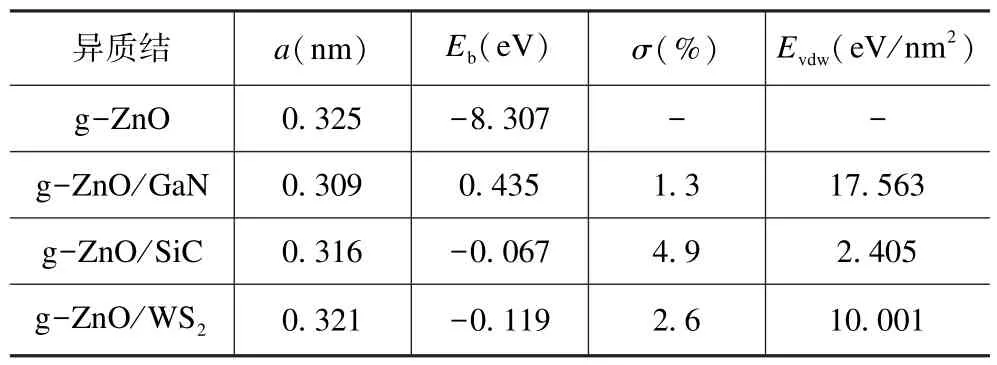
表1 g-ZnO 与g-ZnO/X 异质结的结构参数Tab.1 Structural parameters of g-ZnO and g-ZnO/X heterojunction
2.2 电子结构
电子结构是研究异质结界面特性的关键,图3(a)~(d)表示g-ZnO 和g-ZnO/X 异质结的能带结构图,费米能级设置为E=0 eV。由图3(a)可知,g-ZnO 导带底与价带顶均在高对称点G,表明g-ZnO 属于直接带隙半导体,其带隙为3.270 eV,与文献[51]报道相近,表明计算结果的可靠性。由图3(b)~(d)可知,g-ZnO/X(X=GaN,SiC,WS2)异质结的带隙分别为1.712,2.130,1.646 eV,其导带底与价带顶均在高对称点G,异质结体系均为直接带隙半导体,与g-ZnO 相比,异质结体系的禁带宽度均减小,异质结导带部分均有不同程度的下移,且能级变密集。相较而言,g-ZnO/WS2异质结的禁带宽度最小,电子跃迁所需的能量最小,更有利于提高该体系的光催化能力。

图3 能带结构。(a) g-ZnO;(b) g-ZnO/GaN 异质结;(c) g-ZnO/SiC 异质结;(d) g-ZnO/WS2异质结Fig.3 Energy band structure.(a) g-ZnO;(b) g-ZnO/GaN heterojunction;(c) g-ZnO/SiC heterojunction;(d) g-ZnO/WS2 heterojunction
为了研究其轨道贡献和电子耦合,计算了g-ZnO和g-ZnO/X 异质结的电子态密度如图4 所示,由图4(a)可以看出g-ZnO 的导带部分主要是由Zn 的4s、3p 轨道所贡献;价带部分主要是由O-2p 轨道所贡献,电子跃迁由O-2p 轨道跃迁至Zn-4s 轨道。
异质结的电子态密度并不是两种单层半导体之间的简单叠加,受异质结界面处vdw 作用力和电子轨道耦合的影响,异质结分为跨隙异质结(Ⅰ型),适合用作制氢剂;交错隙异质结(Ⅱ型) 是高效光催化剂[52-53]。图4(b)表明g-ZnO/GaN 异质结中导带部分主要由Ga-4p 和Zn-4s 轨道所贡献,价带部分主要由O-2p 与N-2p 轨道所贡献,属于Ⅱ型异质结,有利于提高体系的光催化性;由图4(c)可以看出,g-ZnO/SiC 异质结中导带部分主要由Zn-4s、Si-3p 轨道所贡献,价带部分主要由O-2s、C-2p 所贡献,其费米能级附近均由SiC 所贡献,属于Ⅰ型异质结,有利于光催化水制氢;如图4(d)所示,g-ZnO/WS2异质结中导带部分主要由Zn-4s、S-3p 轨道所贡献,价带部分主要由O-2p、S-3p 轨道所贡献,属于Ⅱ型异质结,有望成为高效光催化剂。

图4 电子态密度。(a) g-ZnO;(b) g-ZnO/GaN 异质结;(c) g-ZnO/SiC 异质结;(d) g-ZnO/WS2异质结Fig.4 Electronic density of states.(a) g-ZnO;(b) g-ZnO/GaN heterojunction;(c) g-ZnO/SiC heterojunction;(d) g-ZnO/WS2 heterojunction
综合电子结构分析可知,由于异质结界面间、原子间的轨道耦合作用,体系局域化增强,使得异质结能级变密集,只有导带向下发生移动,降低了体系的禁带宽度,相比g-ZnO,异质结拓宽了对可见光的响应范围。其中g-ZnO/X(X=GaN、WS2)异质结为交错排列结构,电子在g-ZnO、X 层(X=GaN,WS2)之间相互交错跃迁,有效分离了电子空穴对,产生了电势差,这更有利于提高体系的光催化活性,初步证实了异质结可以降低光生载流子复合的概率。
2.3 界面电荷转移
采用功函数作为界面电荷转移的参考标准,其计算公式[54]为:

式中:Evacuum代表真空能级;Efermi代表费米能级;g-ZnO、GaN、SiC、WS2功函数分别为6.398,5.032,4.921,5.399 eV,由于功函数的不同,半导体接触后形成异质结,其电子随之发生转移,GaN、SiC、WS2接触形成异质结后的功函数分别为5.165,4.479,5.571 eV。由图5 可知,单层GaN、SiC、WS2的功函数均低于g-ZnO,g-ZnO/X 异质结中电子由X 层向g-ZnO 层转移,随着电子的转移,g-ZnO 与X 层的费米能级发生移动,直至达到相同的能级,故产生了内置电场,内置电场可以有效地促进光生电子空穴对的分离,降低了光生载流子的复合概率,在光照下,光生电子由X 层向g-ZnO 层移动,光生空穴停留在X层,随着电子空穴对的分离形成电势差,有利于提高体系的光催化能力。
为了详细地描述异质结界面电荷转移,计算得到异质结的差分电荷密度。g-ZnO/X(X=GaN,SiC,WS2)异质结界面电荷转移性质如图6(a)~(c)所示,图中褐色表示电子积累,绿色表示电子消耗。由于层间耦合效应,异质结界面的电荷重新分布,由差分电荷密度可以看出,电荷消耗主要集中在X 层(X=GaN,SiC,WS2),电荷积累主要集中在g-ZnO 层,表明电子由X 层向g-ZnO 层转移,电荷转移导致异质结内部形成内置电场,产生了自发极化现象,有利于电子空穴对的分离,内置电场方向为X 层指向g-ZnO层,佐证了图5 功函数计算的电子转移方向。

图5 功函数。(a) g-ZnO;(b) GaN;(c) SiC;(d) WS2;(e) g-ZnO/GaN 异质结;(f) g-ZnO/SiC 异质结;(g) g-ZnO/WS2异质结Fig.5 Work function.(a) g-ZnO;(b) GaN;(c) SiC;(b) WS2;(e) g-ZnO/GaN heterojunction;(f) g-ZnO/SiC heterojunction;(g) g-ZnO/WS2 heterojunction

图6 差分电荷密度。(a) g-ZnO/GaN 异质结;(b) g-ZnO/SiC 异质结;(c) g-ZnO/WS2异质结Fig.6 Differential charge density.(a) g-ZnO/GaN heterojunction;(b) g-ZnO/SiC heterojunction;(c) g-ZnO/WS2 heterojunction
2.4 光电性质
研究异质结的光电性质对光电器件的制备有重要意义。通过计算半导体的介电函数[55],结合Kramer-Kronig 关系[56]可推导出吸收光谱的计算公式:

图7 是g-ZnO 与g-ZnO/X 异质结的光吸收谱图。由图7(a)可知g-ZnO 与g-ZnO/X 异质结的吸收带边分别为3.270,1.712,2.130,1.646 eV,异质结的吸收带边均在可见光范围内(1.60~3.20 eV)。相比g-ZnO 而言,异质结体系在红外、可见光和紫外区域的光吸收率均有所提高,其峰值分别为4.5×104,5.0×104,1.3×105cm-1,说明GaN、SiC、WS2拓宽了g-ZnO 对可见光的吸收范围,其中ZnO/WS2异质结吸收带边最小,吸收率峰值最大,其对可见光的响应能力最强。由光吸收带边nm 图(图7(b))可知,g-ZnO 的吸收带边为350 nm,说明g-ZnO 在长波紫外线及短波可见光具有一定的吸收能力;相较g-ZnO 而言,g-ZnO/GaN、g-ZnO/SiC、g-ZnO/WS2异质结的吸收带边拓宽至680,550,750 nm,由此可知,三种异质结均发生了明显红移,拓宽了其对可见光的响应范围,其中g-ZnO/WS2的红移程度最明显,其吸收系数达到105数量级,与Si[57]的吸收系数相差无几,意味着g-ZnO/WS2具有较宽的可见光响应范围,该异质结可以作为一种高效的光吸收材料应用在光催化领域。
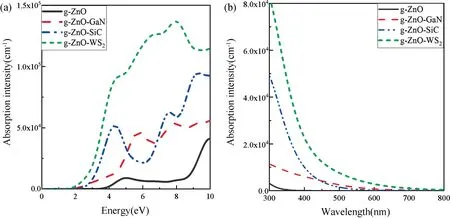
图7 g-ZnO 与g-ZnO/X 异质结的光吸收谱图。(a) eV 光吸收谱图;(b) nm 光吸收谱图Fig.7 Optical absorption spectra of g-ZnO and g-ZnO/X heterostructures.(a) eV light absorption spectra;(a) nm light absorption spectra
图8 是g-ZnO 和g-ZnO/X 异质结的介电函数图,介电函数实部反映了介电常数随入射光子能量的变化,实部越大表明体系对电荷的束缚能力越强,体系的极化能力越强[58]。当光子能量为0 时,对应为静介电常数。g-ZnO 和g-ZnO/X(X=GaN,SiC,WS2)异质结的静介电常数分别为1.239,1.888,2.196,4.798,与g-ZnO 相比,异质结体系的静介电常数都有所增加。g-ZnO/WS2的静介电常数最大,表明该体系极化能力最强,光生电场强度最大,促进了光生电子空穴对的分离,可以有效改善光催化活性。介电函数虚部反映入射光子能量的变化,虚部表示半导体光激发载流子的浓度[58]。与g-ZnO 相比,异质结体系的介电函数虚部均有所增大,表示异质结体系中受激发跃迁的电子更多,异质结体系介电函数虚部均扩展至可见光区域(1.6~3.2 eV),其中g-ZnO/WS2异质结在可见光区域介电函数虚部最大,由结合态密度可知是S-3p 轨道与Zn-4s、3p 轨道间的轨道耦合,表明g-ZnO/WS2异质结从价带跃迁至导带的电子跃迁强度最强,对可见光吸收能力最好。
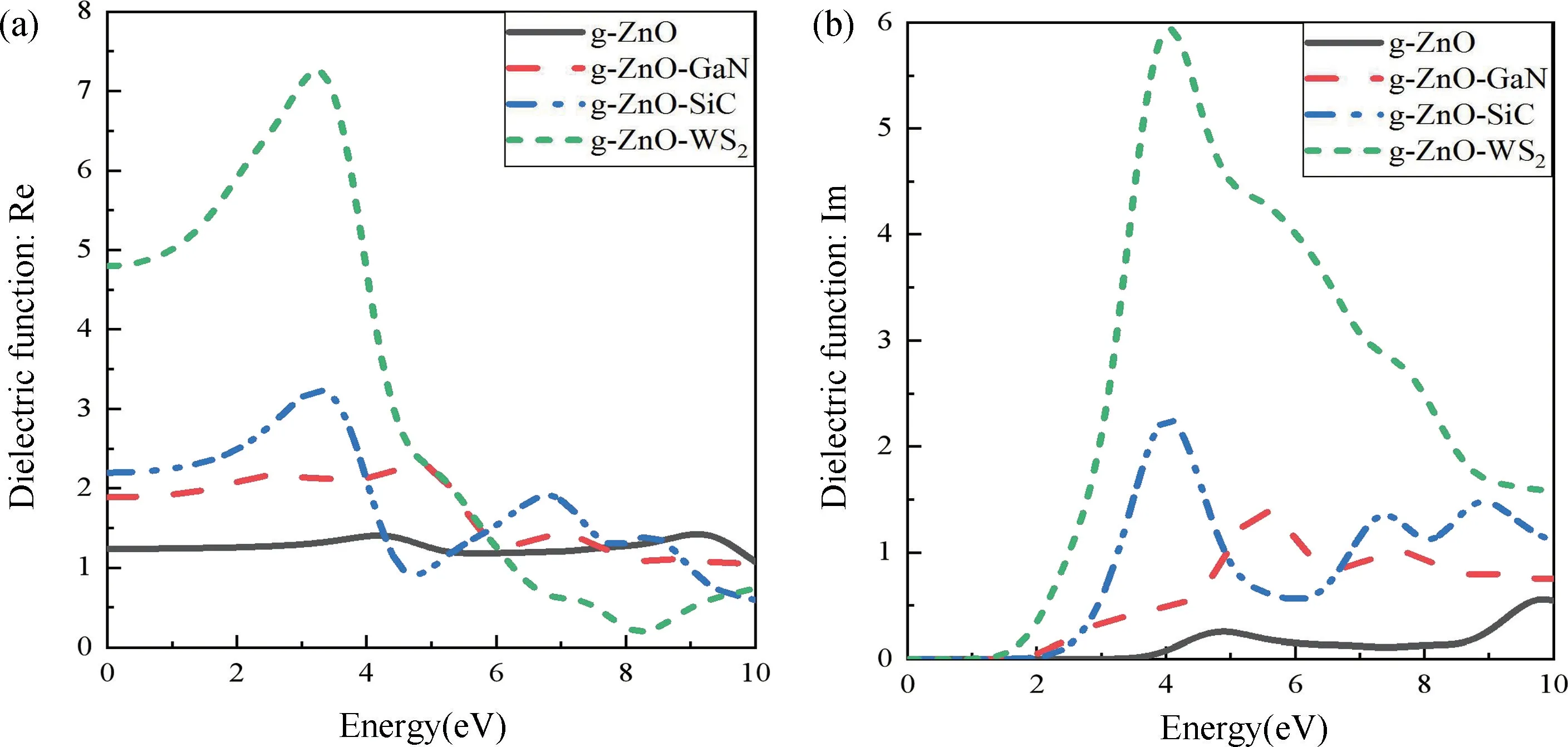
图8 g-ZnO 与g-ZnO/X 异质结的介电函数。(a) 介电函数实部;(b) 介电函数虚部Fig.8 Dielectric function of g-ZnO and g-ZnO/X heterostructures.(a) Real part of dielectric function;(b) Imaginary part of dielectric function
3 结论
本文提出g-ZnO 与单层GaN、SiC、WS2搭建异质结的想法,通过第一性原理计算了g-ZnO 与g-ZnO/X 异质结的晶格失配率、结合能、电子结构及光学性质。研究结果表明,g-ZnO/WS2的结合能最小(-0.119 eV),表明该体系稳定,最容易通过实验制备。通过电子结构分析可知,g-ZnO 和g-ZnO/X 异质结均为直接带隙半导体,带隙均减小,且保持了各组分固有的电子结构,其中g-ZnO/WS2异质结的带隙最小,减小了光生电子跃迁所需的能量,界面间的耦合作用促进了电子空穴对的分离;同时功函数与差分电荷密度验证了这一结论,异质结体系均有电荷转移,产生了内置电场,其方向为X 层指向g-ZnO 层,有效分离了光生电子空穴对,有利于提高体系对可见光的响应能力;光学性质进一步证明异质结体系对可见光具有良好的响应能力,异质结体系均发生红移现象且提高了光吸收强度,其中g-ZnO/WS2异质结吸收带边为1.646 eV,吸收率为1.3×105cm-1,意味着该体系对可见光的响应能力最强、响应范围最广,同时g-ZnO/WS2异质结吸收系数与Si 为同等能量级,表明该异质结体系能覆盖紫外及可见光区域,是一种高效的光吸收材料。
——潘桂棠光生的地质情怀

