基于XFEM的谐波减速器柔轮裂纹扩展行为研究
薛栋文 徐 洋 解国升 赵言正 刘积昊
(1 东华大学 机械工程学院,上海 201620)
(2 上海交通大学 机械与动力工程学院,上海 200240)
0 引言
谐波减速器具有传动比大、运行稳定、传动精度高及负载能力强的优点,被广泛应用于工业机器人、航空航天、能源及精密机床等高精领域[1-2]。通常,谐波减速器是由波发生器、柔轮、刚轮等基本构件组成。谐波齿轮传动的主要失效形式有柔轮疲劳断裂、柔性轴承损坏、齿面磨损等。其中,柔轮疲劳断裂占总失效形式的60%以上[3]。局部微裂纹的形成及扩展是引发柔轮断裂的主要原因[4]。因此,研究柔轮的裂纹形成及裂纹扩展特性,有助于掌握柔轮裂纹生长规律,预测剩余寿命。
目前,关于谐波减速器柔轮的疲劳裂纹研究主要集中在裂纹形成原因及对谐波传动性能的影响方面,对于柔轮的裂纹扩展研究,可查阅文献较少[4-6]。现阶段,国内外很多学者对直齿圆柱齿轮等刚性齿轮的裂纹扩展进行了研究,分析了裂纹形状、载荷对疲劳裂纹扩展及疲劳寿命的影响[7-9],这些研究方法和成果已较为成熟。但是,柔轮裂纹扩展分析与刚性齿轮有所不同。刚性齿轮齿形较大,裂纹形貌和扩展方向相对固定;而柔轮是一种挠性部件,齿圈位于薄壁末端,齿形细密,不易断齿,其裂纹扩展涉及齿圈、筒体及凸缘,受谐波传动、几何形变等多种因素影响。因此,柔轮的裂纹扩展规律异于刚性齿轮,随机性更为显著。
本文中以某型号谐波减速器为研究对象,建立柔轮应力分析模型,确定柔轮应力集中的参数;采用有限元仿真软件分析应力最大区域,在应力最大结点引入微小角裂纹;依据裂尖应力场参量,分析裂纹扩展的趋势和能力;基于扩展有限元方法,对柔轮的疲劳裂纹扩展行为进行分析和预测;最后,通过柔轮加速寿命试验验证了裂纹扩展特性。
1 柔轮结构与应力计算
1.1 柔轮结构及材料属性
如图1所示,谐波减速器的柔轮为中空翻边形标准筒式结构。柔轮材料为合金钢,弹性模量E=2.06×105MPa,泊松比μ=0.28,质量密度ρ=7 800 kg/m³,结构参数如表1所示。

图1 柔轮结构Fig.1 Flexspline structure
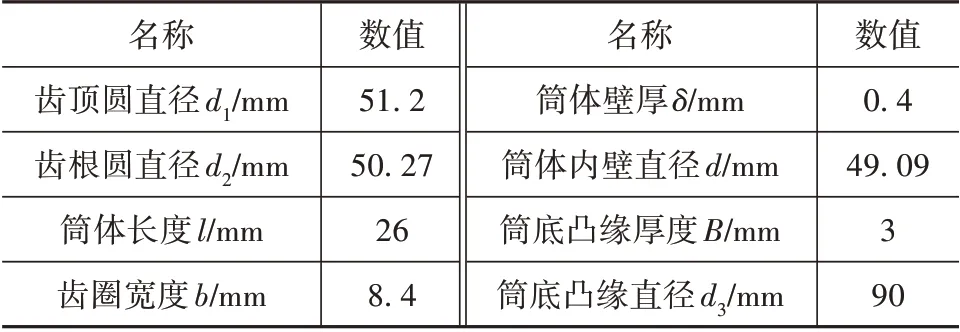
表1 柔轮结构参数Tab.1 Structural parameters of flexspline
1.2 柔轮应力集中位置确定
如图2(a)所示,柔轮应力可基于圆柱壳体的力矩模型,在一定假设下求出[10]206,并根据实际加载情况对应力计算进行修正。图2(b)所示为柔轮变形的端面轮廓。其中,筒体中面半径rm=24.795 mm,长轴处最大径向位移w0=0.5 mm,啮合区角β=30°。基于壳体中面应变为0的假设,在壳体微元上的内力只有在z和φ方向的弯矩和转矩MZ、Mφ、MZφ。

图2 柔轮等效模型Fig.2 Equivalent model of flexspline
MZ引起的沿母线方向的修正正应力为

Mφ引起的沿周向的修正正应力为

MZφ引起的沿z和φ方向的修正剪应力为

转矩T所产生的修正剪应力为

式中,Kd为动载系数;KM为柔轮应力增长系数;Ku为剪应力分布不均匀系数;Cσ为正应力系数;Cτ为剪应力系数。
谐波减速器额定寿命较长,因此,采用3 倍额定负载进行理论计算、仿真及加速实验。由文献[10]213-233查表得该工况下各应力系数,如表2所示。

表2 应力模型修正系数Tab.2 Stress model correction parameters
根据式(1)、式(2),柔轮正应力与z成正比。令z=l时,柔轮端面处应力最大。
2 柔轮三维建模及裂尖应力参量获取
由等效柔轮应力模型初步确定应力集中位置为柔轮齿端面。通过有限元仿真,建立柔轮载荷优化模型,进一步对应力集中位置进行分析,确定微裂纹引入结点,进而可获得表征裂纹扩展能力的各项参量。
2.1 载荷模型优化
图3(a)所示为柔轮受载示意图。柔轮的主要受载有:在柔轮内壁由波发生器迫使柔轮变形而产生的径向载荷P;在柔轮齿圈由柔轮与刚轮齿啮合而产生的齿面载荷F。图3(b)所示为柔轮应力分布云图。
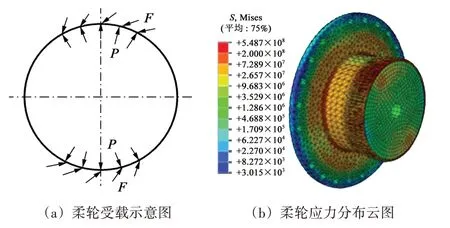
图3 柔轮载荷模型Fig.3 Load model of flexspline
2.2 裂尖应力场参量获取与分析
通过仿真获得柔轮的最大应力结点,在该位置引入微小裂纹。其中,引入的切片半径为0.5 mm,圆心位于最大应力结点,垂直于柔轮齿端面,如图4所示。利用M 积分[11]可求得裂尖从点A(内表面)到点B(外表面)的应力强度因子KⅠ、KⅡ、KⅢ和J积分。
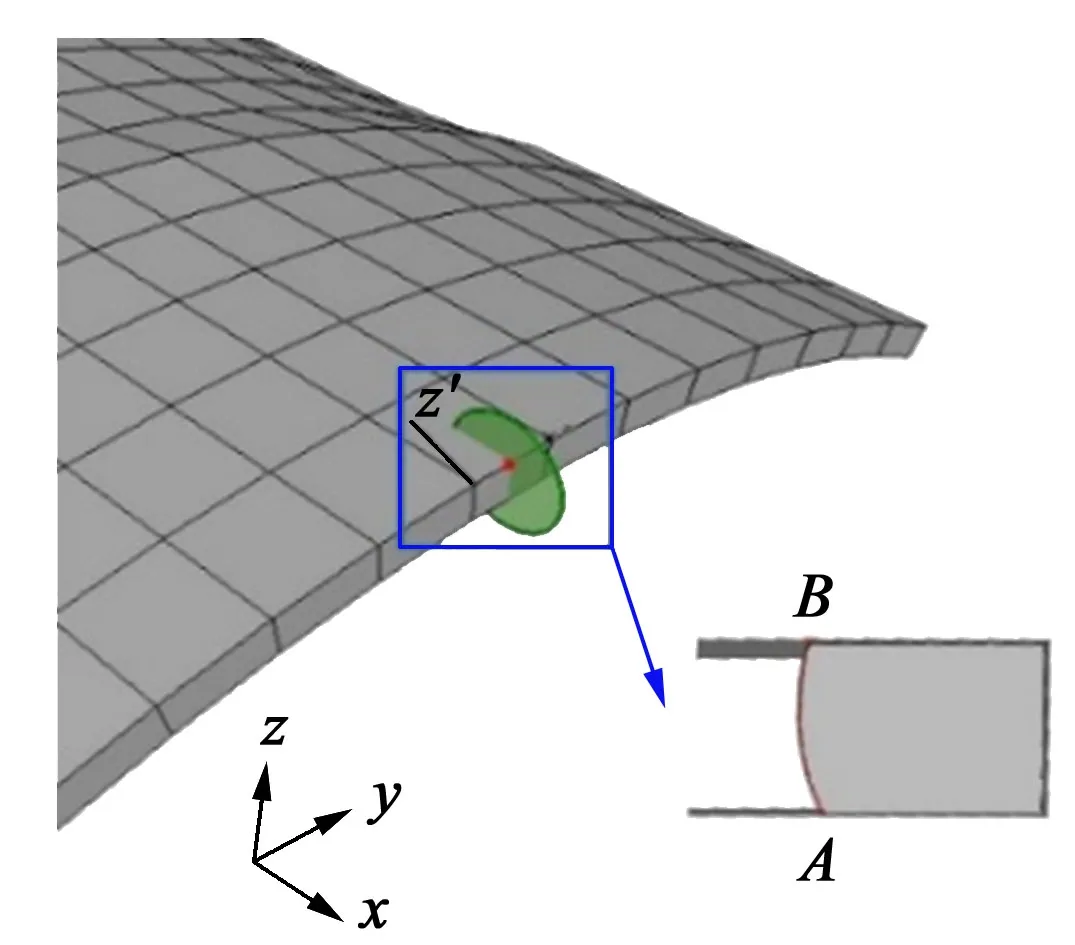
图4 微裂纹引入及截面示意图Fig.4 Schematic of microcrack introduction and section
应力强度因子表征了材料外力作用下物体裂纹尖端附近的应力场强度,显示了裂纹扩展的能力。
KⅠ描述了由正应力引起的应力集中,是表征应力场强弱的主要参量。图5 所示为裂尖由点A到点B的KⅠ分布图。
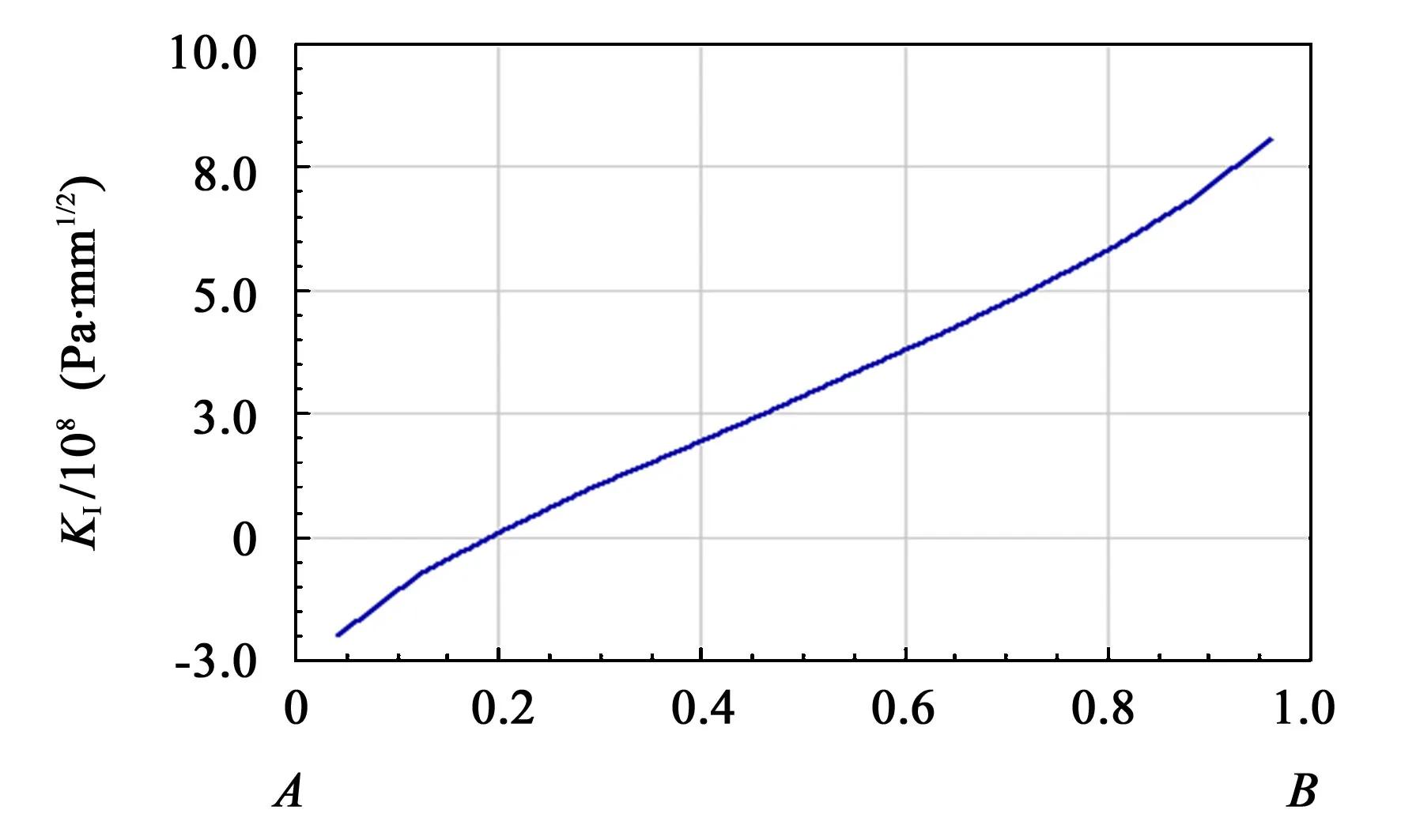
图5 裂尖KⅠ分布Fig.5 KⅠdistribution of crack tip
Ⅱ型裂纹来源于剪应力破坏,裂纹平行于裂纹扩展方向。KⅡ用来预测裂纹扭转角度,以确定裂纹前缘的扩展方向。图6 所示为裂尖由点A到点B的KⅡ分布图。
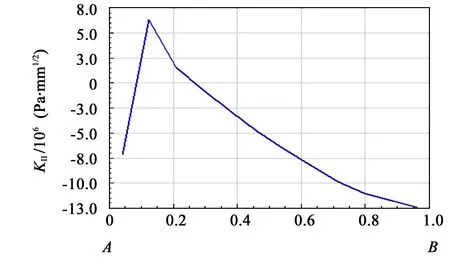
图6 裂尖KⅡ分布Fig.6 KⅡdistribution of crack tip
Ⅲ型裂纹来源于剪应力破坏,裂纹垂直于裂纹扩展方向。KⅢ可描述剪应力集中程度。图7 所示为裂尖由点A到点B的KⅢ分布图。
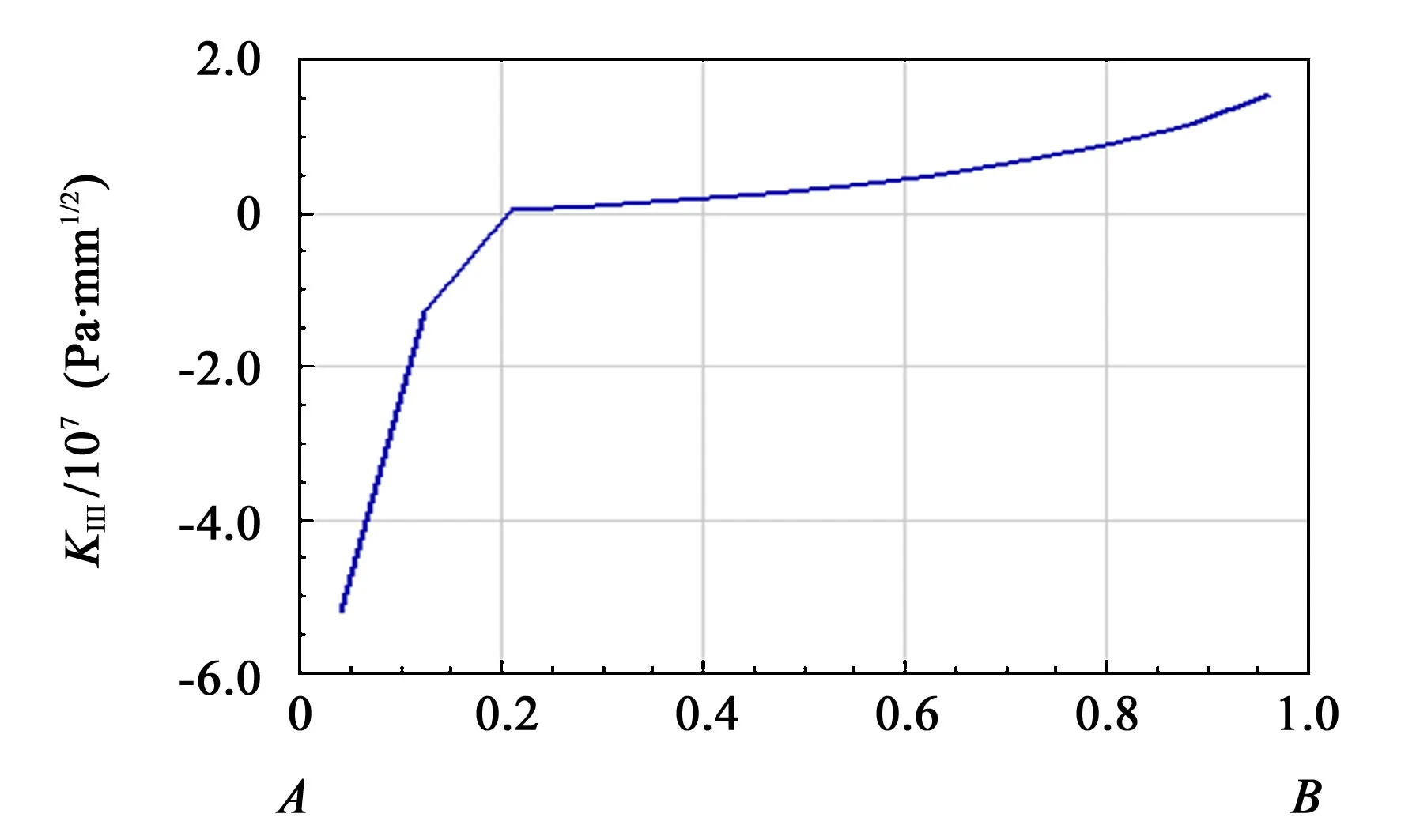
图7 裂尖KⅢ分布Fig.7 KⅢdistribution of crack tip
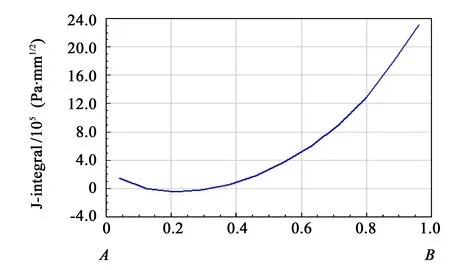
图8 裂尖J积分分布Fig.8 J-integral distribution of crack tip
J 积分是由Rice J R[12]提出的一个围绕裂尖并与路径无关的守恒积分,用来描述裂尖局部集中应力、应变场强度平均值的参量。KⅠ、KⅡ、KⅢ与J 积分关系为
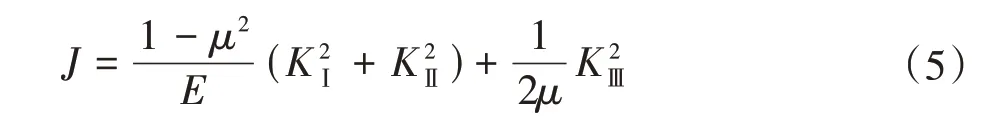
J积分在近A端约1/5处最小,该位置附近出现KⅡ峰值,裂纹最先扩展。J积分在B端达到最大,且KⅠ、KⅢ最大,裂纹附近的应力集中于柔轮外表面。
3 基于XFEM 的裂纹扩展
扩 展 有 限 元(Extended finite element method,XFEM)是一种模拟分析断裂力学问题的有效方法[13-14],其在保留传统有限元算法优势的同时,能够独立于网格剖分解决裂纹扩展问题,不需要对裂纹形成区域和扩展轮廓进行局部网格细化。
3.1 模型简化
由于XFEM 只能采用四边形或六面体网格,且不支持自适应网格。因此,计算时将柔轮模型进行简化,将齿圈以当量圆环代替,删除柔轮模型中的倒角、圆角及工艺孔。
3.2 增量步对裂纹路径的影响
增量步大小直接使相同工况下同一位置的裂纹扩展路径随即改变。载荷施加时,若某一增量步经有限次迭代后仍不收敛,则将增量步大小调整为当前的0.25 倍,重新迭代。若初始增量步设置过大,易导致结果不收敛;设置过小,则时间成本过高。图9、图10 所示为初始增量步大小分别为0.01 和0.001时的裂纹扩展路径仿真结果。
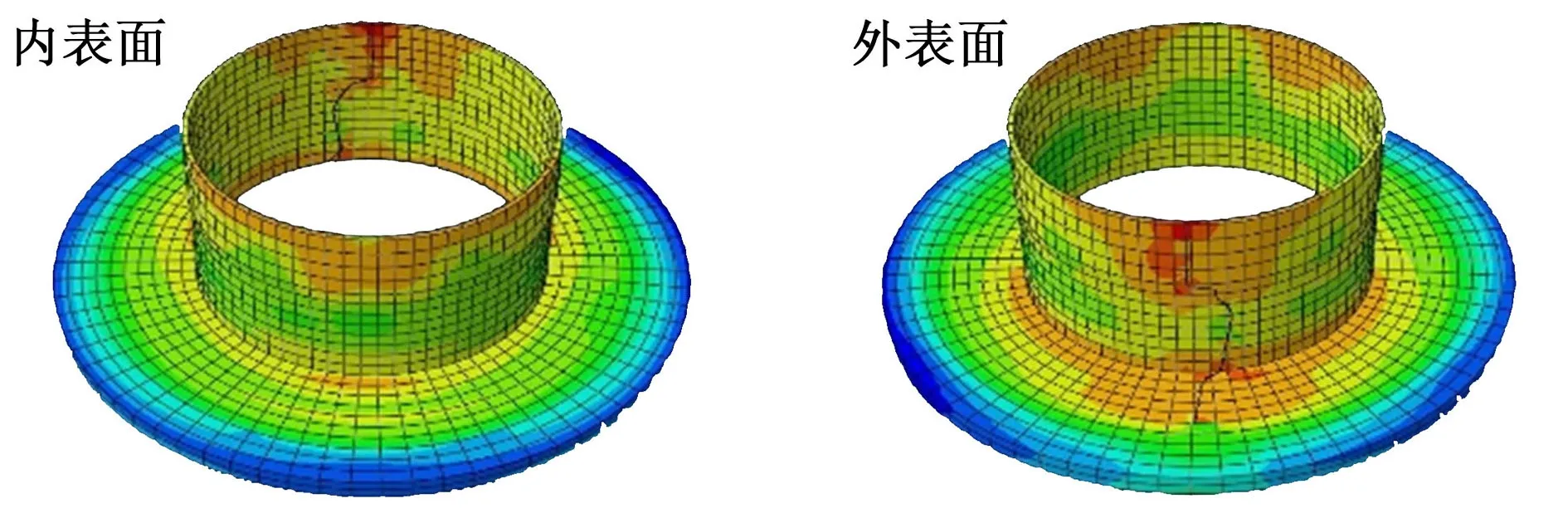
图9 初始增量步为0.01的裂纹仿真图Fig.9 Simulation of cracks with initial increment=0.01
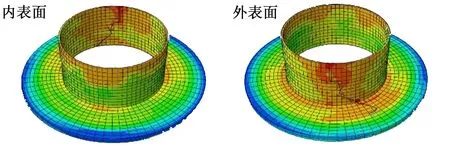
图10 初始增量步为0.001的裂纹仿真图Fig.10 Simulation of cracks with initial increment=0.001
图9、图10中应力分布结果与第2.2节裂尖应力场分析结果一致,裂纹附近的应力分布明显集中于外表面。裂纹的总体扩展趋势相同,增量步大小对裂纹扩展路径的随机差异性的影响显著。
4 疲劳裂纹实验
为验证柔轮XFEM 仿真裂纹扩展路径与实际的差异,搭建了谐波减速器加速寿命试验台,通过采用3倍负载加速破坏的方式得到裂纹的扩展路径。
4.1 谐波减速器加速寿命试验台搭建
如图11所示,试验台主要由变频电机、联轴器、谐波减速器、磁粉制动器等4部分组成。变频电机型号为ABB80M2.4.6P-B3,其额定功率为1.1 kW,额定转矩为3.5 N·m,额定转速为2 845 r/min;联轴器采用膜片式,型号为CPDW50-19-19;磁粉制动器采用兰菱FZ1000J/Y,额定转矩为1 000 N·m,许用转速为1 000 r/min。

图11 谐波减速器加速寿命试验台Fig.11 Accelerated life test bench of harmonic reducers
4.2 破坏形态与裂纹扩展
该系列谐波减速器的额定寿命在9 000 h,需利用过载实验加速破坏。负载设定为3倍额定转矩,转速为2 000 r/min。表3所示为6组加速实验的测试时长。
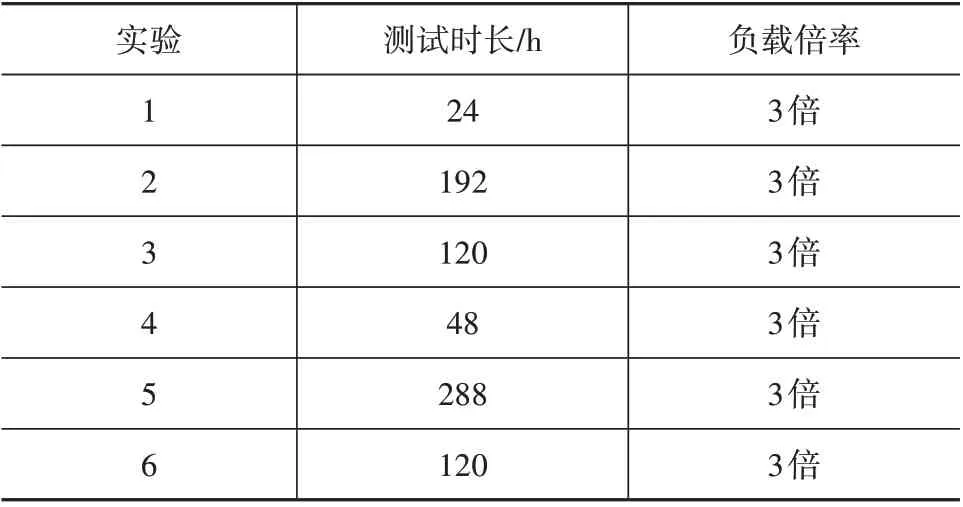
表3 6组实验结果Tab.3 Experimental results of 6 groups
图12 所示分别为加速寿命测试后得到的6 组柔轮裂纹扩展路径。
图12 中,前4 组实验裂纹均与图9 中吻合。前3组实验的裂纹扩展路径与长度相似;实验4的柔轮齿根及筒底与凸缘交界面出现了间断裂纹,两段裂纹沿同一母线,与图9结果一致。


图12 柔轮的损伤形态图集Fig.12 Damage morphology atlas of flexspline
图12 中,实验5 的柔轮裂纹较短,其主要损伤表现为筒体内壁磨损,磨损区域与图10 中的主应力区域重合;实验6的裂纹扩展路径与图10吻合。
分析裂纹路径与仿真结果可知,柔轮裂纹扩展经历了以下几个阶段:
(1)沿齿圈母线开裂。在齿圈区域,受柔轮齿形的限制,波发生器长轴处对柔轮的径向变形作用大于转矩造成的周向变形作用,裂纹沿轴向径直开裂。实际上,由于轮齿间隙相比于轮齿较薄,裂纹在齿根处开裂沿柔轮母线至齿圈结束位置。
(2)沿筒体周向开裂。裂纹扩展至无齿区域,受轮齿形状限制减弱,裂纹沿扭转方向开裂,扩展路径第一次出现明显偏折。由应力云图(图3(b))可知,筒体中段为应力较小区域,相比于齿圈和筒底,裂纹轴向扩展趋势明显,扩展路径第二次出现明显偏折。实际裂纹在扩展至此段时也都出现了不同程度的偏折。
(3)沿凸缘偏折。裂纹扩展至凸缘处时,再次进入应力较大区域,主要裂纹类型逐渐由III 型裂纹变为I型裂纹。裂纹向端面的应力较大位置偏折。
5 结论
以某型号谐波减速器为研究对象,探究了柔轮裂纹扩展行为。基于圆柱壳体的力矩模型,建立柔轮应力分析模型,确定了柔轮应力集中的参量;采用有限元软件重点对应力最大区域进行分析,通过引入裂纹并分析裂尖应力场参量,表征了裂纹扩展能力;最后,基于XFEM 模拟裂纹扩展路径,对疲劳裂纹扩展行为进行了仿真和预测,并通过实验验证了仿真的正确性。得到以下结论:
(1)柔轮裂纹最易出现在柔轮齿根部分及筒体与凸缘交界位置,且总是沿应力最大路线进行扩展。
(2)裂纹尖端处应力更集中于柔轮外表面,裂纹由近内表面5分位点处最先扩展。此外,仿真中增量步大小对裂纹路径的随机差异性影响显著。
(3)裂纹扩展过程中,首先沿齿圈母线开裂,随后因细微载荷差异,主应力区域变化不同,对裂纹扩展路径出现多次偏折的位置和程度影响不同。

