基于深度强化学习的移动机械臂末端滑模控制技术
朱引行
(江苏省涟水中等专业学校,江苏 涟水223400)
引言
近年来,随着机器视觉技术的不断创新与发展,相关领域的研究也得到了进一步深入,最具代表性的便是移动机械臂的控制与应用。在智能化与伺服控制技术的辅助下,移动机械臂的应用范围逐渐扩大,应用效果明显提高。但是,由于人们对于自动化标准的提升,传统的控制技术已经无法满足需求和标准,部分移动机械臂在高强度的工作环境下,末端的滑模逐渐显现出一定的问题与缺陷,对于日常的工作会形成不定性的消极影响。移动机械臂的末端滑模是一项十分关键且重要的控制元件[1],应用中起到“承上启下”的作用,不仅能够加强机械臂对于指令的接收速度,同时,进一步拓展了机械臂的移动空间,逐步营造稳定的工作环境[2]。但是过度移动导致滑模出现裂缝、破损等问题,对于日常的移动、振动控制会形成一定的阻碍[3]。因此,本次结合深度强化学习原理,设计优化移动机械臂末端滑模控制技术,以此为进一步完善整体的应用效果。考虑到最终测试结果的可靠性,选择较为真实的目标作为测试的对象,根据移动机械臂的应用需求、标准,对滑模的控制形式以及范围作出对应的调整。当处于复杂环境下时,滑模的控制压力也会得到缓解,从整体上降低对机械臂的阻碍,更加快速、稳定地完成伺服任务,同时也具有自主定位和跟踪的能力,具有关键的现实应用意义。
1 设计移动机械臂末端滑模单元控制技术
1.1 自适应预处理
在对深度强化学习下移动机械臂末端滑模控制技术进行优化设计之前,需要先结合移动机械臂的作用区域,进行自适应预处理[4]。所谓自适应预处理,主要是针对于机械臂滑模的控制环境,设定的一种动态的控制协议。结合深度强化学习原理,增设辨识机制、非线性动力模型以及异常定位装置,加强对移动机械臂末端滑模的自适应控制程度[5]。利用关联设备,先获取部分基础控制数据,完成汇总整合之后,为确保自适应控制环境的稳定,需要先计算出滑模预设移位率,具体如公式(1)所示:
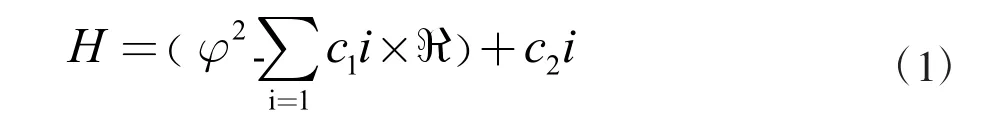
式中:H 表示滑模预设移位率,φ 表示收敛系数,i 表示定向辨识时限,表示自适应滑动比,c1便是预设移位距离,c2表示实测移位距离。通过上述计算,最终可以得出实际的滑模预设移位率。将其预设为滑模的移位标准,同时,关联机械臂内部的非线性控制系统,结构中需要安装自适应感知设备,同时,增加提高轴孔装配、目标捕获等装置,从整体上增加机械臂的自适应控制速度与安全程度,确保自适应控制系统的稳定性,完成自适应处理,为后续的控制处理奠定基础条件。
1.2 布设多模态感知滑模控制节点
结合实际的控制标准,布设一定数量的多模态感知控制节点。提取机械臂滑模的移动特征,加工控制系统与核心感知节点相关联,但需要注意的是,整个过程必须要结合机械臂视觉伺服的控制律。为避免感知失败问题的出现,需要在特定的环境之中,设定一个限制控制区域,导入控制特征,具体的原理,见图1。

图1 多模态感知原理图
根据图1,可以完成对多模态感知原理的设计与调整,针对于移动机械臂的应用范围,调整末端滑模的偏移方向,同时需要设定两侧的偏移指标数值。完成基础调整之后,可以先测定此时节点收集的末端滑模控制数据是否发生较大变化,如果与基础数值对比,出现的差值较大,则需要重新设定个偏移指标,确保控制程序的稳定执行,一定程度上也有利于多模态感知控制节点对机械臂末端滑模的控制。
1.3 多协调控制轨迹设计
在完成对多模态感知控制节点的布设之后,接下来,需要设计多协调控制轨迹。通常情况下,多指令机械臂日常工作效率要比单指令机械臂更高,主要是由于其内部的程序可以同时针对多个目标处理,实现多维度的同步控制,还可以适应较多的应用场景,以此应用效果更佳。可以采用控制指令来代替传统的数字化轨迹控制目标,形成稳定的指令集群,构建多协调的控制程序,将多个目标控制轨迹作为约束条件,增设在不同的主从控制和约束环境之中,结合混合控制算法,计算出机械臂间的同步误差,具体如下所示:

式中:F 表示机械臂间的同步误差,ϑ 表示同步响应时间,א 表示协调范围,μ1表示约束轨迹距离,μ2表示无向图放松约束轨迹距离,n 表示控制次数。通过上述计算,最终可以得出机械臂间的实际同步误差。在标定的误差范围之内,可以合理调整移动机械臂的覆盖区域和控制范围,结合预设的控制约束条件,实现轨迹的定向同步。但是需要注意的是,针对于移动机械臂的控制轨迹,通过多协调的模式,营造拓扑轨迹测定约束框架,并形成一种定向的阻抗,加强末端滑模的移动速度,与末端的执行器响应接触,提升工作精度,降低控制误差。
1.4 构建深度强化学习末端滑模控制模型
在完成对多协调控制轨迹的设计之后,接下来,需要结合深度强化学习原理,构建末端滑模控制模型。首先,需要先将机械臂中的轴孔与轴入孔接触,形成对应的操作空间,控制处理过程中,冲击碰撞是难以避免的,为降低对末端滑模的影响以及损坏,可以引入Hogen 提出阻抗机制,在交互环境之中,结合所获取的数据信息,计算出此时滑模的阻尼系数。随着机械臂的移动与应用,测定分析滑模阻尼系数的变化状态,调整滑模控制模型的指标数值,具体见表1。
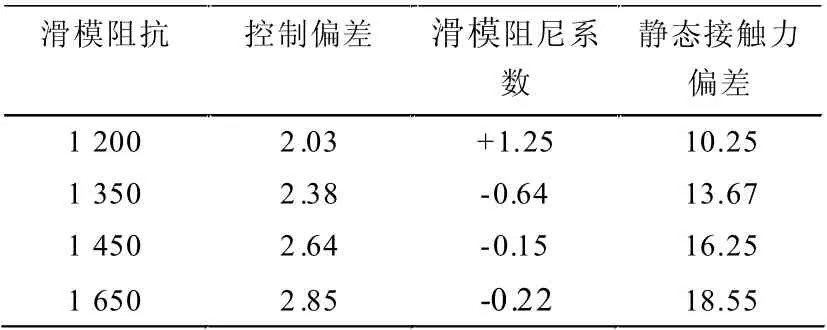
表1 滑模控制模型指标数值设定表
根据表1,可以完成对滑模控制模型指标数值的设定。随后,根据调整的状态,防止工件损坏,将滑模与接触设备形成一种定向的动态联系,设计末端滑模的阻抗控制结构。扩大实际的控制范围,并对标定的控制程序和结构作出调整。通过改变惯性、阻尼系数以及刚度参数来调整动态控制联系,实现多维度的深度强化学习处理。此时,采用深度强化技术,计算出标定的控制修正量,具体如下所示:
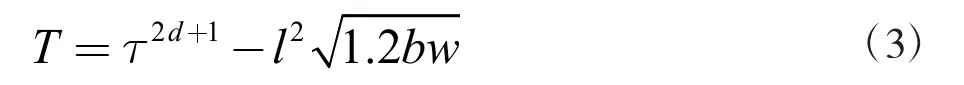
式中:T 表示控制修正量,τ 表示滑模深度强化距离,d表示单向移位时间,b 表示目标位置,w 表示测定位移,l 表示深度接触力。通过上述计算,最终可以得出实际的控制修正量,设定模型的控制范围,并与设定的控制节点相互关联。
1.5 PD 双向控制矩阵设计
结合PD 控制技术,根据末端滑模的控制需求、标准,设计对应的双向控制矩阵。首先,利用控制模型,先获取移动机械臂的实时数据及信息,并在标定的转换范围之内,测定出机械臂在移动过程中的稳态误差,具体见表2。
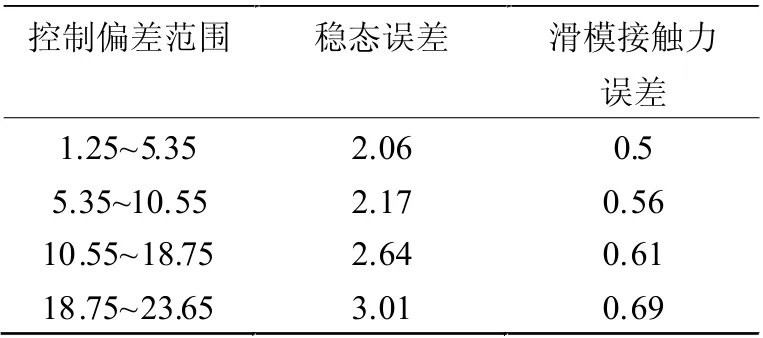
表2 机械臂移动稳态误差测定表
根据表2,可以完成对机械臂移动稳态误差的测定与分析。由于滑模在不同的环境下出现的偏差不同,因此,针对于滑模变动的刚度系数,测定出机械臂滑模的实际力位控制效果。但是需要注意的是,为了保证控制程序的稳态,好需要加强对滑模接触状态的控制,此时可以结合上述测定出的数值,设计PD 双向控制矩阵,设定稳态误差等于0 时,滑模的刚度系数为1.25 以下,控制程序的接触力误差为5.25;而当稳态误差小于或者大于0 时,滑模的刚度系数为1.25 以上,控制程序的接触力误差为10.45~20.35 之间,此时末端滑模的控制轨迹为呈现出侧向的曲线,利用阻抗模型关联二阶控制平台,设定双向控制环节,结合深强化学习技术,结合动态响应模式,构建矩阵的对应控制原理,具体见图2。

图2 深度强化学习下PD 双向控制矩阵原理图示
根据图2,可以完成对深度强化学习下PD 双向控制矩阵原理的设计,结合上述环节,划定末端滑模具体的控制矩阵,同时结合强化学习技术,建立ke 与xe 的误差控制极限点,尽量控制减少稳态误差,并在合理的范围之内,对滑模的移位情况作出调节,增强末端控制的动态与静态控制效果。
2 方法测试
2.1 测试准备
选择G 企业的机械臂作为测试的主要目标对象,并设定传统伺服定位控制技术(方法1)测试组、传统改进分数控制技术(方法2)测试组以及本文所设计的深度强化学习控制技术测试组。结合自抗扰控制与深度强化学习技术,构建改进ESO 的滑模控制程序,并设定机械臂末端滑模的基础指标参数:单元抖振次数5 次,有效控制距离15.35 m,末端变动误差2.03。
2.2 测试过程及结果分析
在标定的测试环境之中,设定三个扰动节点,布设在机械臂的控制节点之中,在控制程序之中,设计滑模面的动态控制环节,确保达测定标准即可。设定标准的抖振比为1∶3.5,测定机械臂在移动的过程中控制系统的鲁棒性,并测算末端滑模的转动惯量,一般需要控制在1.75~6.45 之间,确保滑模可以顺利移动,降低整体的移位偏差概率。结合深度强化学习技术,在周期之内,定位滑模的移动位置,并对其出现的稳态误差进行分析,具体见图3。

图3 末端滑模稳态误差局部变化图示
根据图3,可以完成对末端滑模稳态误差局部变化的分析与研究。经过观测可以的差值,经过控制调整和处理,末端滑模的稳态误差得到了明显的控制,逐渐趋于平稳,这表明误差逐渐减少。此时,启动设定的三个扰动节点,设定处理目标,确保在相同的环境之下,计算出单元控制时间,具体如下所示:

式中:R 表示单元控制时间,η1表示预设扰动范围,η2表示实测扰动范围,ϕ 表示实时转动惯量差值,V 表示等效控制距离。通过上述计算,最终可以得出实际的单元控制时间。结合上述的测试结果,采用对比的形式展开分析,具体见表3。

表3 单元控制时间测试结果对比分析表(s)
根据表3,本研究方法将单元控制时间均控制在了1.5 s 以下,控制的速度与效率表现较好,具有实际的应用价值。
3 结论
结合深度强化学习设计移动机械臂末端滑模控制技术。利用深度强化学习原理,逐步构建统一的滑模控制标准,从根源上降低整体的控制误差,增强度滑模控制的反向作用能力,再加上异常定位技术与末端监测技术的辅助,可以营造更加细化的控制模式,为后续的技术创新奠定参考依据。

