ICP-OES法测定高纯金中银含量的不确定度评定浅析

李 园

（深圳百泰投资控股集团有限公司检测中心，广东 深圳 518083）

Au999%的金合金样品采用GB/T 38145-2019 ICP差减法来测定其杂质元素，用差减法求其主含量。整个检测过程，通过评定Au999%中银含量的不确定度来验证该方法的不确定度，评定该检测方法的不确定度，实验如下：

1 实验

1.1 仪器设备及试剂

检测中心使用的ICP为美国安捷伦科技有限公司的ICP-5110型电感耦合等离子体发射光谱仪。

电子天平为梅特勒的XS205DU（十万分之一）精密天平。

50ml A级容量瓶；100ml A级容量瓶。

银、铜、铁、锌等1000ug/ml标准溶液（国家有色金属及电子材料分析测试中心），实验室用水均为超纯水；实验室硝酸和盐酸均为优级纯。

1.2 样品前处理

把样品压成薄片，剪碎，混匀，称取样品500mg，溶解于10ml王水中，加热赶去氮氧化物，加稀盐酸定容至50ml容量瓶中，摇匀待测。

1.3 检测方法

用ICP-OES来检测标准溶液及样品中杂质的含量，通过差减法来求得金含量。配制6个不同浓度的标准溶液，每种标准溶液重复测试2次；待测溶液重复测试11次。

2 不确定度评定

2.1 数学模型

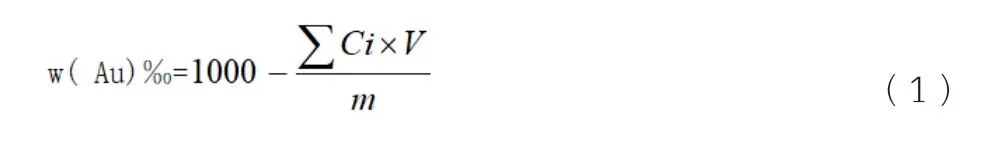
ΣCi为试样溶液杂质元素的浓度和，mg/L。

2.2 不确定度主要来源

称量样品天平引入的不确定度；

定容体积引入的不确定度；

标准溶液浓度引入的不确定度；

重复性分析引入的不确定度。

3 不确定度分量的评定

测试的样品，主要含有银元素，同时含有少量的其他元素杂质元素。通过计算模型知道，总的测量不确定度是通过各元素不确定度来获得，现在，从杂质元素含量来进行判断，含量很少的杂质元素（元素含量少于万分之一），其对应的不确定度对总的不确定度贡献不大，因此，我们当做银含量为杂质总量考虑。如下表1。

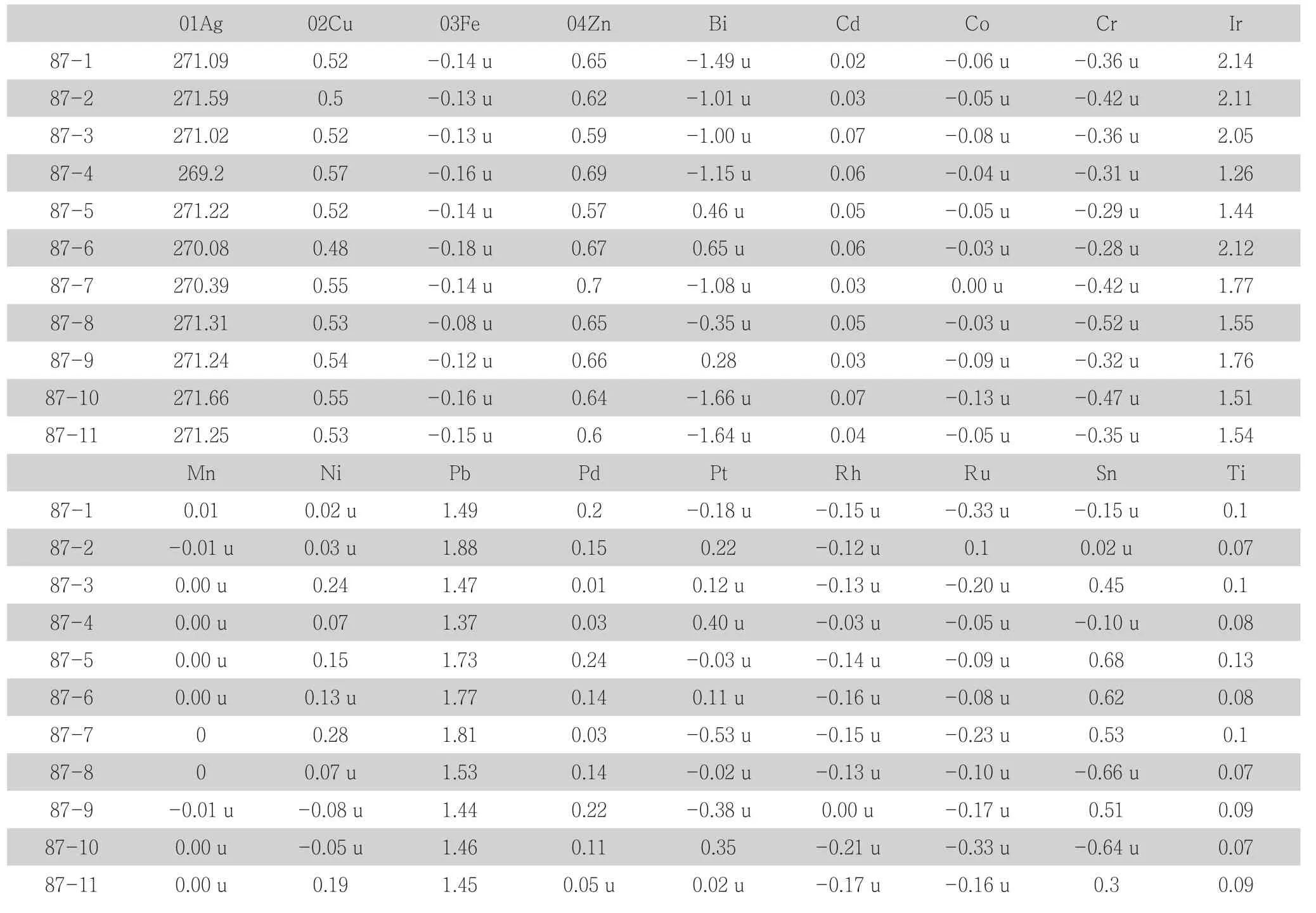
表1 样品测试杂质元素标准含量

由表中可知，其他杂质含量很低，可以通过求该仪器检出限可知，其他含量均低于检出限，那么其他杂质元素由银含量作为杂质总量计算较为科学合理。

3.1 称量样品天平引入的不确定度

该样的质量是由天平称出，其不确定度来源于两个方面：称量量的示值误差、天平的最大允许偏差。

3.1.1 称样量的示值不确定度U（m1）

天平的分辨率为0.01mg，天平分辨率的半宽α为0.05mg，，那么示值的不确定度

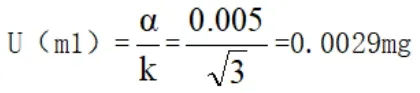
3.1.2 天平的最大允许偏差不确定度U（m2）

查天平校准证书，得知十万分之一电子天平的最大允许偏差为0.05mg，假设为均匀分布，求得标准不确定度为

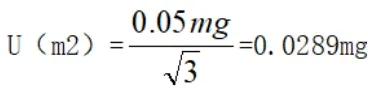
3.1.3 计算合成标准不确定度

假设各分量之间均为独立分量，互不相关，则有

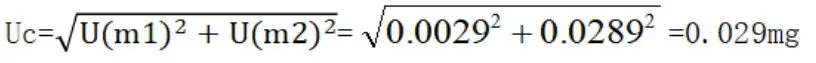
则相对标准不确定度为：

3.2 样品溶液定容体积引入的不确定度

试样溶液定容于50mL容量瓶中，其体积不确定度一般包括；容量瓶本身的不确定度、定容重复性和实验室温度波动三个影响分量。由于方法的测量重复性已经参与计算，其中包括了定容的重复性，因此不予考虑。

3.2.1 玻璃容量瓶本身的不确定度

检测过程中容量瓶为50mL，A级，查检定规程得知，50ml、A级容量瓶最大允许误差±0.05ml,容量瓶定容服从三角分布，，那么u（V1）=0.05/=0.02mL

3.2.2 温度波动带来的不确定度

该容量瓶在20℃校准，实验室温度波动在±5℃之间变化，液体的体积膨胀明显大于容量瓶的体积膨胀，因此，仅需要考虑液体体积变化即可。水的体积膨胀系数为2.1x10-4/℃，因此，产生的体积变化：±（50x5x2.1x10-4）=±0.05mL，假设温度变化为均匀分布，即：

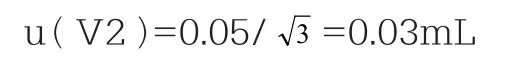
3.2.3 计算定容体积引入的合成标准不确定度

则相对标准不确定度为：

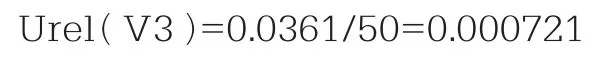
3.3 标准溶液引入的不确定度

标准样品引入的不确定度包括标准溶液的配制以及标准曲线的拟合。而标准溶液的配制引入的不确定度主要由标准溶液、定容体积以及移液枪的不确定度组成。

3.3.1 标准溶液配制引入的不确定度

标准溶液本身的不确定度：

使用的标准溶液主要考虑银元素的标准溶液，银标准溶液（国家钢铁材料测试中心钢铁研究总院）浓度为1000mg/L，扩展不确定度U=4μg/mL，扩展因子k=2，则对应的标准不确定度为：u（c1）=4/2=2μg/mL

相对标准不确定度为：

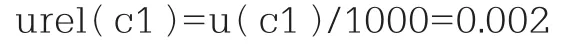
移取标准溶液引入的不确定度：

根据GB/T38145-2019高含量贵金属合金首饰金铂钯含量的测定ICP差减法检测方法，需要配置100mg/L的银校正溶液，再分别移取0、0.2、0.5、1、2、5mL的银标准溶液定容于100mL容量瓶中。查检定证书得：1mL移液枪的扩展不确定度为U=0.008mL，扩展因子k=2，对应的标准不确定度为：

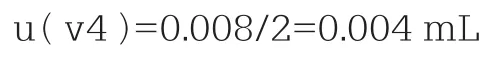
移取标准溶液体积引入的相对标准不确定度为：

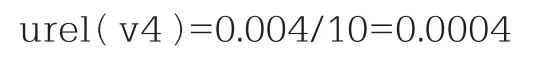
标准溶液定容体积引入的不确定度：

标准溶液定容于100mL玻璃容量瓶中，其体积不确定度一般包括；容量瓶本身误差、定容重复性和实验室温度波动三个影响分量。由于方法的测量重复性已经参与计算，其中包括了定容的重复性，因此不予考虑。

玻璃容量瓶本身的标准不确定度：

作业指导书中要求用100mL玻璃容量瓶，则对应的标准不确定度为：稀释过程中容量瓶为100mL，A级，查检定规程得知，100ml、A级容量瓶最大允许误差±0.1ml，容量瓶定容服从三角分布，，那么

温度波动带来的不确定度：

该容量瓶在20℃校准，实验室温度波动在±5℃之间变化，液体的体积膨胀明显大于容量瓶的体积膨胀，因此，只需要考虑液体体积变化即可。水的体积膨胀系数为2.1x10-4/℃，因此，产生的体积变化：±（100x5x2.1x10-4）=±0.105mL，假设温度变化为均匀分布，即：

计算标准溶液定容体积引入的合成标准不确定度：

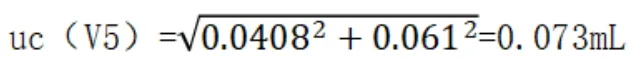
则相对标准不确定度为：

计算标准溶液配制引入的合成相对不确定度：

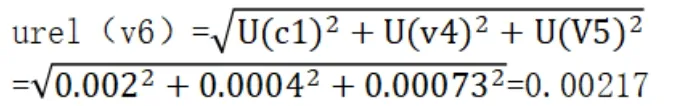
3.3.2 标准曲线拟合引入的不确定度

根据GB/T38145-2019标准方法，标准溶液需要配制空白溶液和校正溶液，通过仪器输出的光谱强度，得到y(强度)=50848(浓度)+36线性回归方程，相关系数为0.99998，计算得到SL=863。

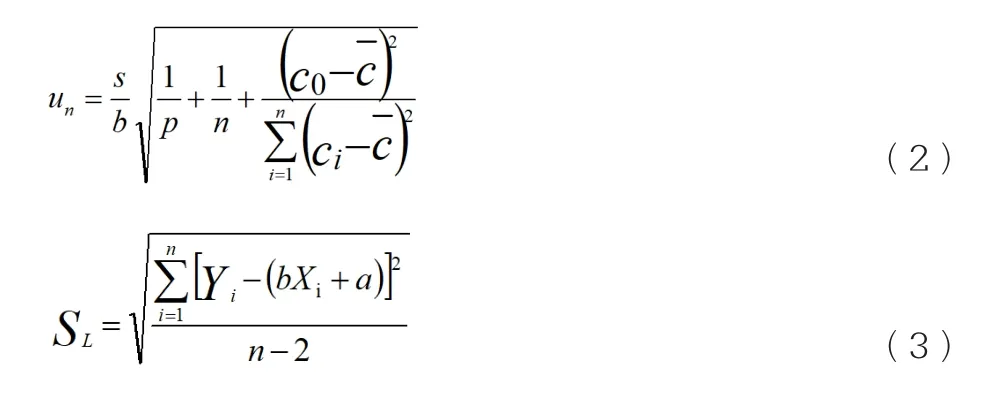
公式（2）和（3）中 ：

un-从校准曲线求C0时引入的不确定度；

SL-从校准曲线求得强度Y与对应的Yi测得值之差按照贝塞尔公式求出标准偏差；

P-样品溶液的测定总次数；

n-为标准溶液测定的总次数；

C0-样品溶液中测定元素浓度；

Ci-标准溶液中测定元素浓度的测定值（即Xi）；

-标准溶液中测定元素浓度的平均值；

Yi-标准溶液的测定元素的光谱强度；

根据表2、表3把数据代入公式（2）和（3），标准曲线拟合引起的相对标准不确定度为Un=0.672，Un，rel=0.000672。

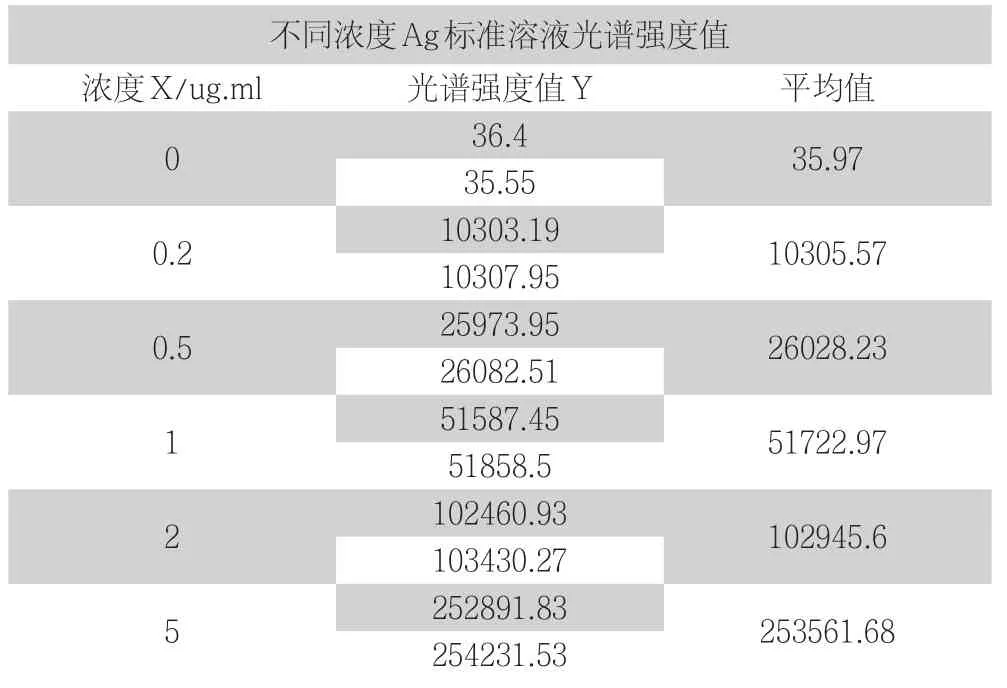
表2 标准曲线光谱强度

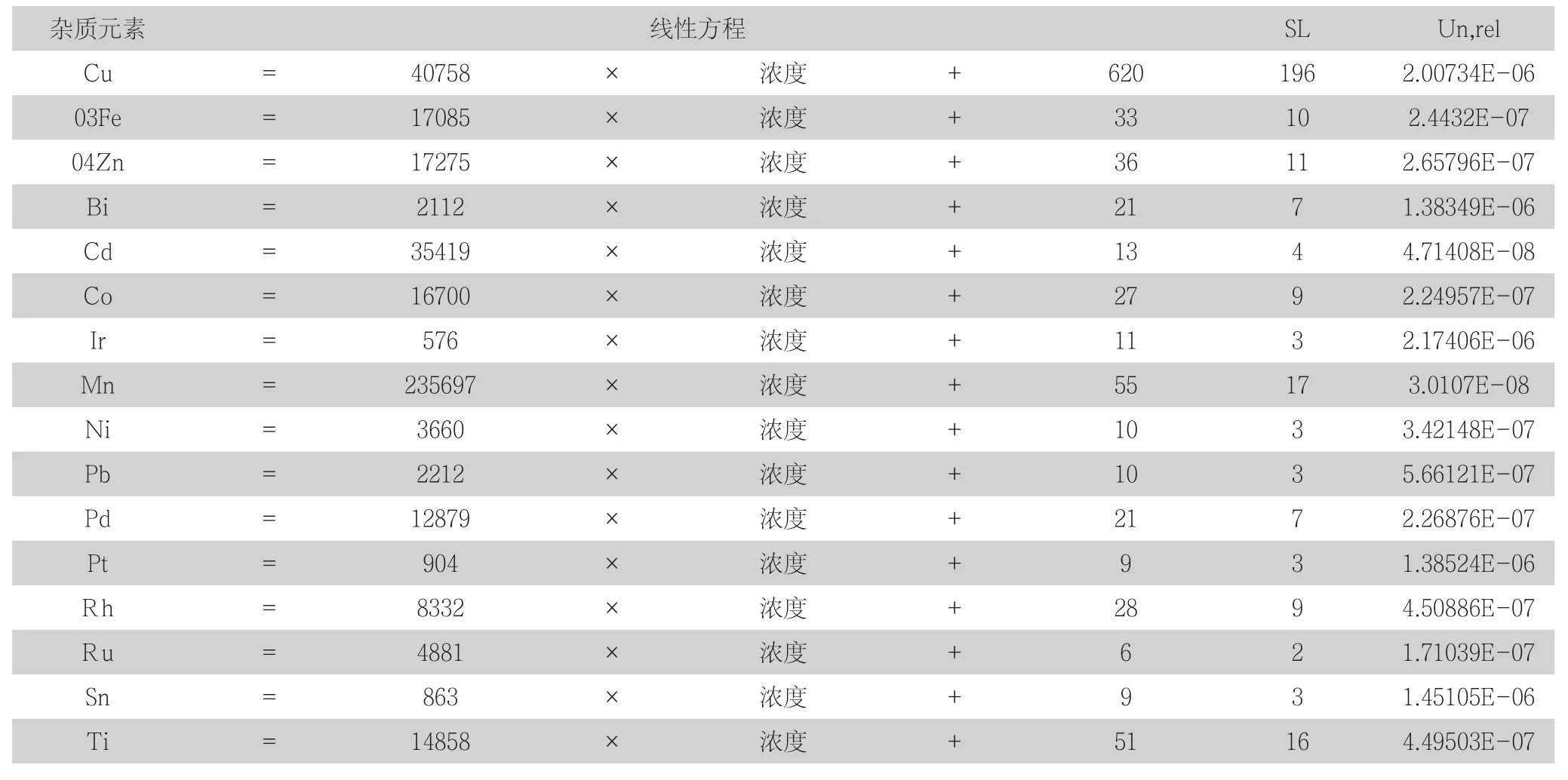
表3 样品杂质元素SL和Un,rel

3.3.3 各个影响因素互不相关，标准曲线引入的不确定度

3.4 重复性引入的不确定度

独立重复测量11次该样品，得到杂质含量如上表1：重复性测试结果如上表1，标准偏差s（贝塞尔公式）及相对不确定度Ucrel计算公式如下式（5）。

公式（5）中，m-样品溶液的测定次数。

4 不确定度分量合成、拓展不确定度

4.1 不确定度分量合成

因各分量之间，互不相关，将以上所得不确定度分量带入，合成相对不确定度：

因为除银外其他杂质元素低于1‰，不予考虑，可近视将银元素的不确定度看做总的不确定度，即u（Ci）=u（Ag）。

测得样品中银杂质含量为2.72ug/ml，银含量的不确定度u（Ag）=0.00256x0.272‰ =0.00069632‰

4.2 拓展不确定度

假设包含因子k=2，相应的相对扩展不确定度为：

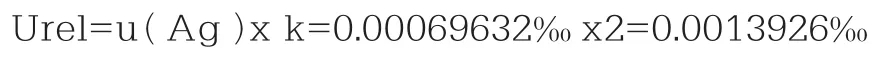
由数学模型

得知，其传播系数为

5 结果与讨论

5.1 结果

被测样品杂质元素银含量测定结果可表示为：

(Ag)‰ =｛（270.91±1.3926）/1000｝‰，其中相对拓展不确定度Urel=0.0013926‰，k=2是由相对标准不确定度和包含因子k=2的乘积得到的。由传播系数得知，Urel,△C=0.034815‰。

按照检测标准GB/T 38145-2019进行分析测定，被测样品的金含量是通过差减法得到最终的结果，根据以上评定结果得出，其它杂质元素含量不确定度的贡献很小，对测试结果影响可忽略不计。如果不考虑其他杂质的不确定度，可以根据计算公式可得样品金含量：

5.2 说明

方法GB/T 38145-2019高含量贵金属合金首饰金铂钯含量的测定ICP差减法计算不确定时基体效应影响没有考虑进去，根据本实验室的实际情况编写了该不确定度，作为该方法不确定度计算的参考依据。

方法GB/T 38145-2019高含量贵金属合金首饰金铂钯含量的测定ICP差减法计算不确定度时进行了方法偏移，标准方法中标准溶液浓度和个数进行了偏移，在计算重复性引入不确定度已经进行了偏移，根据实验室本身实际做出的不确定度可作为该方法的不确定依据和贡献。

方法GB/T 38145-2019高含量贵金属合金首饰金铂钯含量的测定ICP差减法在本实验中测定金合金首饰金含量的测定，仅计算了金合金首饰中的杂质元素，使用的是GB/T 38145-2019标准方法推荐的波长（附录C，表C.2），其中个别波长使用其他波长。