两级节流中间完全冷却CO2跨临界双级压缩制冷循环特性研究
牛 恒 肖寒松 李无言 王佩卿 张显鹏 石文星
(1 清华大学建筑技术科学系 北京 100084;2 南京久鼎环境科技股份有限公司 南京 211000)
CO2是一种绿色环保的天然制冷剂,1850年美国科学家A. Twining最早提出将CO2用于蒸气压缩制冷系统,T. Lowe于19世纪70年代研发出用于食品冷冻运输船舶的CO2制冷系统[1],此后因卤代烃类制冷剂的发展,CO2逐渐被淘汰。然而,在发现卤代烃对臭氧层有破坏效应并会产生温室效应后,研究人员又重新重视对CO2制冷剂的应用研究。由于CO2临界温度低,用于船舶时可利用低温海水进行冷凝降温,故最早设计的CO2制冷系统采用的是亚临界循环。随着CO2跨临界循环的提出,采用气体冷却器代替冷凝器,目前被广泛应用于空调[2]、热泵[3]、核反应堆冷却[4]等领域。
跨临界循环制冷系统中的制冷剂在超临界区的温度与压力相互独立,二者共同影响其比焓值。当工况条件确定后,特别是当蒸发温度与气冷器出口温度确定后,排气压力高低将同时影响制冷量和输入功率,其最大制冷系数COPmax(coefficient of perfor-mance)对应的排气压力称为最优排气压力pdopt[5]。对于单级循环,已有大量学者进行了研究,1928年,H. Inokuty[6]通过几何图解法最早给出了单级理论循环的最优排气压力pdopt,S;Liao S. M. 等[7]通过模拟分析,指出了气冷器出口温度、蒸发温度和压缩机性能将同时影响单级系统的最优排气压力;J. Sarkar等[8]研究表明,气冷器出口温度和蒸发温度对COP的影响比回热循环和压缩机等熵效率的影响更为显著。
对于跨临界双级压缩制冷循环,已有学者对不同类型制冷循环的最优排气压力或最优中间压力进行研究,对主要循环的研究结果如表1所示。此外,张振迎等[12]对表1中的循环(a)和循环(c)进行了研究,结果表明,在常规空调工况下,循环(c)的制冷系数COP高于循环(a),当蒸发温度位于-10~10 ℃范围时,两种循环的COP比单级循环分别提高了32.3%和18.7%。刘圣春等[13]通过热力学计算分析得出,二次节流形式的COP远大于一次节流形式,中间不完全冷却与完全冷却形式的COP几乎相同。王洪利等[14]对比了表1循环类型(a)中带回热器与不带回热器时其最优中间压力的关系,发现带回热器的循环最优中间压力相比于不带回热器循环时降低5%~15%。

表1 CO2跨临界双级压缩制冷循环最优排气压力的研究结论Tab.1 The research conclusion on optimal discharge pressure of CO2 transcritical two-stage compression refrigeration cycle
目前,应用于低温冷库的CO2跨临界循环制冷系统通常采用两级节流中间完全冷却双级压缩制冷循环(简称:DTCC循环),它与表1中循环(d)的区别在于低压级压缩机排气管上设置低压级气冷器并采用回热循环。然而,现有研究未考虑低压级排气采用外部冷却介质进行预冷以及回热方式对性能的影响问题,且其压缩机的容积效率和等熵效率也多取为定值。因此,本文将综合考虑压缩比对压缩机容积效率ηv与等熵效率ηs的影响,建立数学模型,通过遍历工况,分析蒸发温度te、压缩机等熵效率ηs、气冷器出口温度tgs、排气压力pd以及回热循环方式等因素对DTCC循环与跨临界单级压缩制冷循环(简称:单级循环)COP的影响,从而获得DTCC循环的最优排气压力pdopt, D关联式,并分析其与单级循环最优排气压力pdopt, S的关系,为系统的优化设计与控制提供理论指导。
1 DTCC循环工作原理及数学模型
1.1 工作原理
图1(a)所示为DTCC循环的工作原理。制冷剂在系统中的循环流程为:经回热器加热后的制冷剂(1′)进入低压级压缩机,其排气(2)经过(采用冷却水的)低压级气冷器预冷后(3)进入闪蒸罐中;从气冷器中流出的超临界流体(6)经高压级膨胀阀节流后(7)进入闪蒸罐,闪蒸出的饱和气体与被中压饱和液体冷却后的低压级排气混合后(4),一同进入高压级压缩机,高压级排气进入高压级气冷器中冷却降温至超临界流体(6,温度为tgs);闪蒸罐中的中温饱和液体(8)经过回热器再冷后(8′),经低压级膨胀阀节流后(9)进入蒸发器,在蒸发器内吸热蒸发至饱和蒸气(1),再经回热器加热后返回低压级压缩机,完成循环。图1(b)所示为对应图1(a)的制冷循环压焓图,其中,状态点下标中的“s”表示等熵压缩后的终点,c为CO2的临界状态点(tc=31.1 ℃,pc=7.38 MPa)。
1.2 数学模型

为分析DTCC循环的pdopt,D,需建立其部件和制冷循环的数学模型。
1.2.1 压缩机
压缩机是蒸气压缩式制冷系统的核心部件,由于其容积效率和等熵效率受压缩比的影响较为显著,因此对高、低压级压缩机均采用文献[15]基于实验拟合的等熵效率ηs关联式和文献[16]给出的容积效率ηv建立压缩机模型,即:
ηs=0.801 4-0.048 42ε
(1)
ηv=-0.009 6ε2+0.006 5ε+0.85
(2)
其中,εl=pm/pe,εh=pd/pm。
1.2.2 闪蒸罐
针对图1所示的系统原理,基于质量守恒和能量守恒,可以得到闪蒸罐数学模型,即:
mlh3+mhh6=mlh8+mhh4
(3)
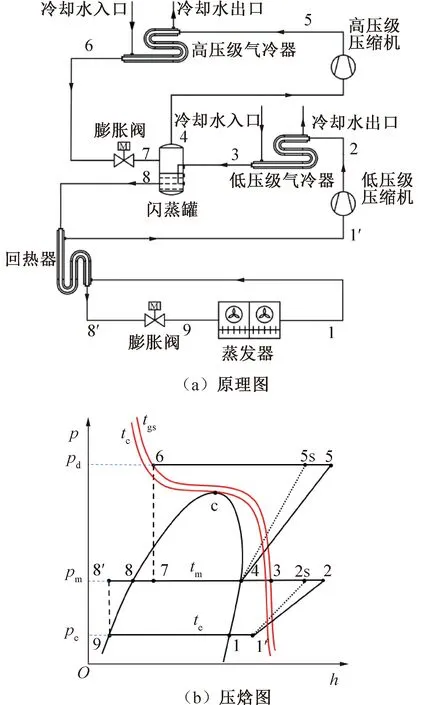
图1 DTCC循环工作原理Fig.1 Working principle of DTCC cycle
1.2.3 气冷器
图1中的低压级与高压级气冷器出口3点与6点的温度与外部冷却介质(冷却水)的温度有关。设气冷器为逆流换热,冷却水进水与制冷剂出口侧的换热端差为3 ℃,高压级与低压级气冷器出口的制冷剂温度相同,均为:
tgs=tw+3
(4)
在模拟计算中,当低压级排气温度(2点)t2≤tw+3 ℃(即t2≤tgs)时,则将2点的制冷剂直接利用闪蒸罐中的中压液体蒸发进行冷却降温。
1.2.4 回热器
DTCC循环具有两种回热方式,即图1所示的低压级吸气与闪蒸罐出口的中温液体回热(简称:中温回热循环)和图2所示的低压吸气与高压级气冷器出口的高温流体回热(简称:高温回热循环),其回热器模型分别如式(5)和式(6)所示。
h1′-h1=h8-h8′
(5)
ml(h1′-h1)=mh(h6-h6′)
(6)
式(6)中比焓值的下标对应图2中的状态点。
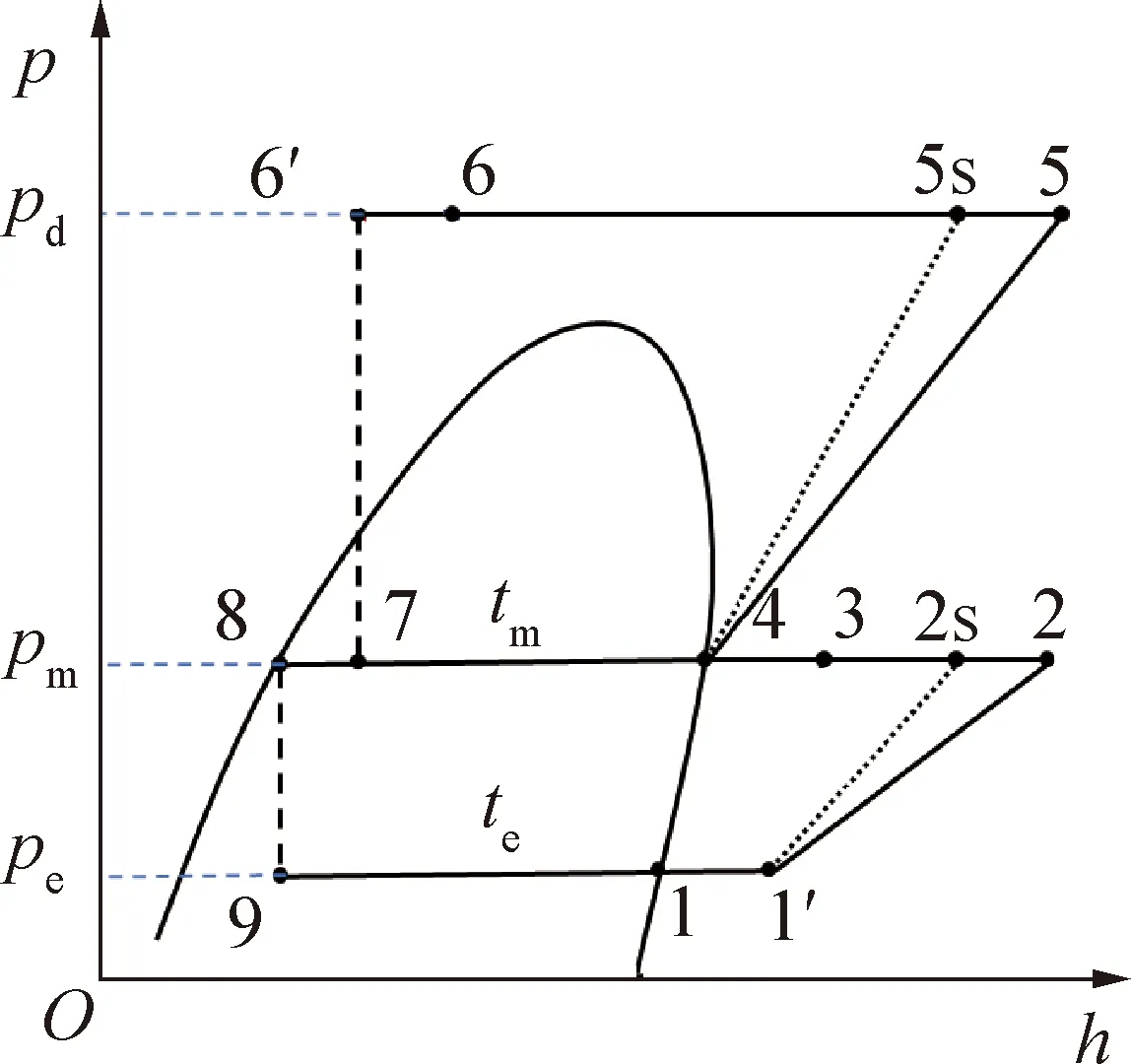
图2 高温回热循环压焓图Fig.2 p-h diagram of high temperature recuperative cycle
1.2.5 DTCC循环
在进行循环计算时,当给定te、tgs,高、低压级压缩机吸气过热度及理论输气量时,改变高压级压缩机pd,则可利用式(1)~式(11)计算出对应工况下的高、低压级质量流量、输入功率、制冷量与COP。
ml=Vlρ1′ηvl
(7)
Wl=ml(h2s-h1′)/ηsl
(8)
Wh=mh(h5s-h4)/ηsh
(9)
Qe=ml(h1-h9)
(10)
(11)
图3所示为模拟计算的流程图。当其他工况条件确定后,每改变一次pd后,遍历计算在pe与pd之间的所有pm,获得计算范围内COPmax所对应的排气压力,即该工况下的最优排气压力pdopt,D。

图3 pdopt,D的计算流程图Fig.3 The calculation flow chart of pdopt,D
2 各参数对最优排气压力的影响分析
在模拟计算中,选择ηs、te、tgs、回热循环方式(以Δtsh大小反映回热器容量大小,当无回热循环时,取Δtsh=0 ℃)为独立变化条件,从热力学循环角度定量分析各因素对DTCC循环和单级压缩跨临界循环的最优排气压力(pdopt,D和pdopt,S)的影响程度。
2.1 压缩机等熵效率
在tgs=35 ℃、te=-15 ℃、Δtsh=0 ℃时,ηs对DTCC循环COP的影响如图4所示。由图4可知,ηs直接影响压缩机的输入功率,对循环COP影响显著,但对pdopt,D的影响较小,pdopt,D仅随ηs的降低略有降低。这与文献[17]中给出的ηs对pdopt,S的影响结果一致。

图4 DTCC循环在不同ηs条件下COP随pd的变化Fig.4 Variation of COP with pd in DTCC cycles at different ηs
2.2 蒸发温度
设tgs=33 ℃(即冷却水入口温度tw=30 ℃)、Δtsh=0 ℃,在不同te下,分析单级与DTCC循环COP的变化规律以及对应的pdopt,S与pdopt,D,结果如图5所示。
由图5可知,当te从0 ℃变化至-30 ℃时,DTCC循环在各te下的COP均高于单级循环。当te=0 ℃时,单级、DTCC循环的pdopt,S与pdopt,D分别为8.175 MPa和7.950 MPa;当te=-30 ℃时,pdopt,S与pdopt,D分别为8.220 MPa和8.095 MPa。单级和DTCC循环的最优排气压力随te的降低略有升高,各te下的COPmax连线几乎垂直于横坐标轴,表明te对两种循环各自的最优排气压力影响并不显著。
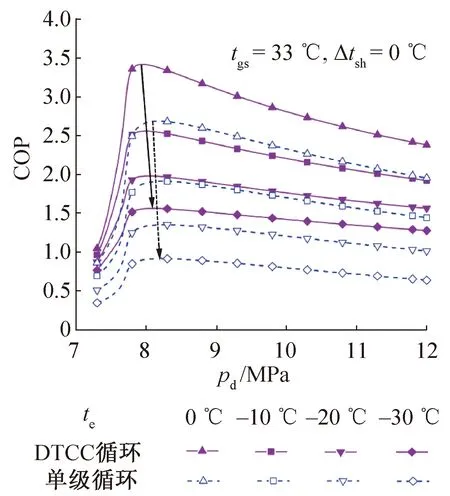
图5 单级与DTCC循环在不同te条件下COP随pd的变化Fig.5 Variation of COP with pd in single stage and DTCC cycles at different te
2.3 气冷器出口温度
在te=-15 ℃、Δtsh=0 ℃时,tgs和pd对单级与DTCC循环COP的影响如图6所示。由图6可知,DTCC循环在不同tgs下的COP均高于单级循环,但随着tgs的升高,DTCC循环与单级循环的COP差值变小。在跨临界循环状态下,当tgs=32 ℃时,单级和DTCC循环的pdopt,S与pdopt,D分别为7.975 MPa和7.685 MPa;当tgs=38 ℃时,pdopt,S与pdopt,D分别为9.550 MPa和9.225 MPa,分别升高1.575 MPa和1.540 MPa。分析可知,在相同tgs条件下,单级循环的最优排气压力略高于DTCC循环,两者在不同tgs时的最优排气压力连线几乎平行。

图6 单级和DTCC循环在不同tgs条件下COP随pd的变化Fig.6 Variation of COP with pd in single stage and DTCC cycles at different tgs
2.4 回热方式
为探究图1(b)和图2所示的采用中温和高温回热循环时DTCC循环的性能特点,对两种回热方式的pdopt,D进行分析。
中温与高温回热循环在te为-10 ℃和-20 ℃,Δtsh分别为0(无回热循环)、5、10、15 ℃时pdopt,D的计算结果如图7所示。

图7 DTCC中温与高温回热循环tgs、te和Δtsh对pdopt,D的影响Fig.7 Effects of tgs、te and Δtsh on pdopt,D in DTCC middle temperature and high temperature recuperative cycle
可以看出二者的共同特点:
1)当te和Δtsh一定时,tgs升高,两种回热循环的pdopt,D均升高;
2)当Δtsh和tgs一定时,两种回热循环的pdopt,D随te的降低而略有升高趋势;
3)当tgs和te一定时,随着Δtsh的增大,两种回热循环的pdopt,D有微小的降低。
分析可知,中温与高温回热循环的pdopt,D均主要取决于tgs的高低,而受te和Δtsh的影响较小,但中温回热循环的Δtsh和te对pdopt,D的影响比高温回热循环略大。
以te=-10 ℃、tgs=35 ℃为例,通过改变Δtsh来分析两种回热方式对DTCC循环的COP和pdopt,D的影响,结果如图8所示。由图8可知,在计算值范围内,当pd<8.0 MPa时,两种回热循环的COP相差很小;但当pd>8.0 MPa时,随着Δtsh的增大,两种回热循环的COP相对于无回热循环时均得到改善,但高温回热循环的改善程度更大;同时还可知,两种回热循环的pdopt,D几乎相等,而与回热循环的Δtsh相关性极小。

图8 pd和Δtsh对DTCC高温和中温回热循环COP的影响Fig.8 Effects of pd and Δtsh on COP in DTCC high and middle temperature recuperative cycle
3 最优排气压力分析
图9所示为Δtsh=0 ℃时,单级和DTCC循环在不同te下pdopt随tgs的变化。由图9可知,当tgs升高时,单、双级循环的pdopt,S、pdopt,D均上升,且在不同te下,单、双级循环的pdopt,S、pdopt,D几乎分别相同。

图9 单级与DTCC循环的pdopt与tgs的关系Fig.9 Relationship between pdopt and tgs in single stage and DTCC high temperature recuperative cycle
根据前文分析可知,pe和回热循环的Δtsh对DTCC循环pdopt,D影响较小,因此可忽略循环的pe和Δtsh影响,仅考虑tgs对pdopt,D的影响,通过拟合分析,从而得到pdopt,D以及在相同te和tgs条件下的pdopt,S与tgs的函数关系:
pdopt,D=0.250 9(tgs-tc)+7.534
(12)
pdopt,S=0.250 9(tgs-tc)+7.833
(13)
式(12)与式(13)的适用范围:pe=1.4~4.5 MPa(te=-30~10 ℃),tgs=tc~45 ℃,pd=pc~12.0 MPa,pdopt,D和pdopt,S的计算误差均在5%以内。
由pdopt,D、pdopt,S表达式可知:在不同tgs条件下,单级与DTCC循环的最优排气压力的差值约为一个定值0.3 MPa,即DTCC循环的pdopt,D可采用相应工况的pdopt,S进行计算,只需从其结果中减去0.3 MPa即可。
4 最优中间压力分析
中间压力pm的选取不仅影响部件之间的优化匹配关系,还将影响DTCC循环的COP。对其最优中间压力pmopt进一步分析。
4.1 中间压力对循环性能的影响
在tgs=35 ℃、te=-15 ℃、Δtsh=0 ℃条件下,pd与pm对DTCC循环COP的影响如图10(a)所示,图10(b)是图10(a)在pd为8.5、9.5、10.5、11.5 MPa处的截面图。综合图10(a)和图10(b)可知,当pm逐渐增大时,COP先增大后减小,存在pmopt。

图10 DTCC循环的最优中间压力pmoptFig.10 Optimal intermediate pressure pmopt in DTCC cycle
由图10(a)可知,DTCC循环在pm=4.78 MPa时出现了曲面的突变现象,对应图10(b)中4个pd下的A、B、C、D转折点。在图10(b)中,曲线从转折点处,右半部分成了实、虚两条曲线,反映了低压级气冷器对COP的贡献效果。以A点为例,A点右侧实线表示越过A点对应中间压力pm后,低压级排气温度高于冷却水进水温度,低压级气冷器发挥了很好的预冷效果;A点右侧虚线表示无低压级气冷器时的循环性能。对比分析可知,相比于无气冷器时,采用低压级气冷器能较大程度地改善循环性能,此时,DTCC循环的pmopt比传统最优中间压力计算式(14)的计算值偏高约5.5 MPa,参见图10(b)中的Δpm。
(14)
4.2 DTCC循环的最优中间压力
在tgs=35 ℃、te=-30~0 ℃、Δtsh=0 ℃和15 ℃条件下,采用两种回热方式下的pd与pmopt的关系如图11所示。

图11 te与Δtsh对高温和中温回热循环pmopt的影响Fig.11 Effects of te and Δtsh on pdopt,D in DTCC high and middle temperature recuperative cycle
由图11可知,当te不同时,中温回热DTCC循环的pmopt与无回热时几乎相同,但高温回热DTCC循环的pmopt比无回热循环时偏低0.13~0.28 MPa,且随te的降低其偏差变小。
在tgs=35 ℃、Δtsh=0 ℃条件下,在不同te时DTCC循环的pmopt和计算出的中间压力pm如图12所示。由图12可知,在不同te下,pmopt呈现相似的变化趋势,且随te的升高而增加,其转折点发生在pd=9.0 MPa附近。因此,DTCC循环的pmopt与pd和pe的关系可根据pd范围表示为如下的分段函数(式中的压力单位为kPa),即:

图12 te与pd对pmopt的影响Fig.12 Effects of te and pd on pmopt
较高排气压力时(pd=9.0~12.0 MPa):
(15)
较低排气压力时(pd=7.3~9.0 MPa):
pmopt=8.127-0.055pd+0.084pe
(16)
式(15)的适用范围:pe=1.4~4.5 MPa(te=-30~10 ℃),tgs=30~45 ℃,pd=9.0~12.0 MPa,Δtsh=0~15 ℃;式(16)的适用范围:pe=1.4~4.5 MPa(te=-30~10 ℃),tgs=10~35 ℃,pd=7.3~9.0 MPa,Δtsh=0~15 ℃。在上述工况范围内,高温与中温回热DTCC循环pmopt的计算误差分别小于5%和10%。
DTCC循环在tgs=35 ℃、Δtsh=0 ℃时分别采用式(14)~式(16)计算出的COP如图13所示。由图13可知,采用传统公式(14)设计的DTCC循环,最大COP比根据拟合公式(15)与(16)设计的循环约低8%。
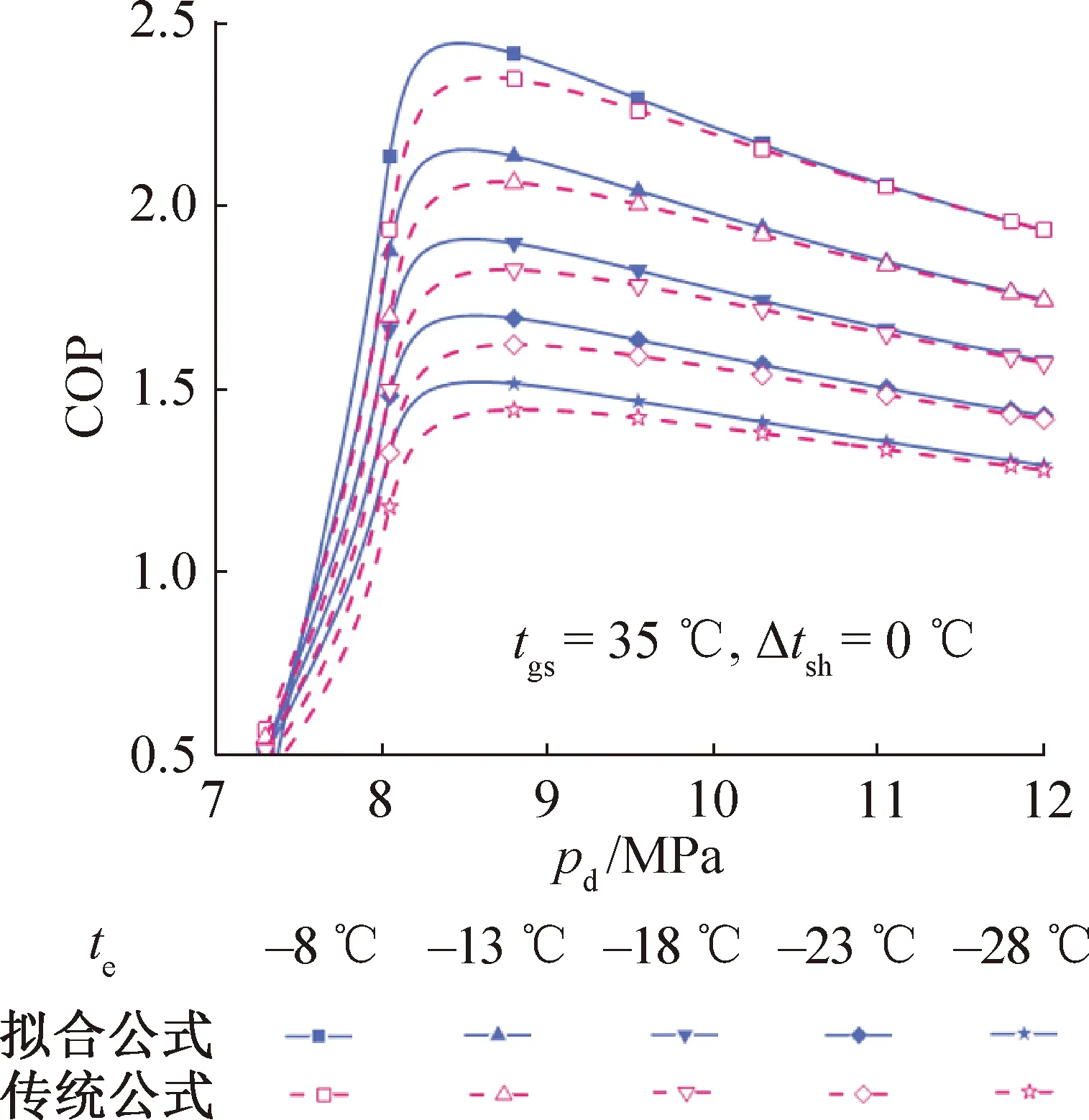
图13 采用两种pm计算式的COP计算结果Fig.13 Results of COP by using two pm calculation formulas
5 结论
CO2是环保型天然制冷剂,其两级节流中间完全冷却跨临界双级压缩制冷循环(DTCC循环)在低温冷库中得到了应用。为研究其循环特性,本文建立了数学模型,通过模拟不同工况条件,分析循环各主要状态参数、回热方式以及低压级气冷器对COP的影响,得到如下结论:
1)DTCC循环的最优排气压力主要取决于气冷器出口温度,而与压缩机效率、蒸发温度、是否回热的关系较小,据此给出了DTCC循环的最优排气压力的计算式;分析表明,在蒸发温度为-30~ 10 ℃、气冷器出口温度在31.1~45 ℃范围内,DTCC循环的最优排气压力约比相同工况下的单级跨临界制冷循环最优排气压力低0.3 MPa。
2)在相同气冷器出口温度条件下,低压级吸气与闪蒸罐出口液体换热的中温回热DTCC循环和低压级吸气与高压级气冷器出口流体换热的高温回热DTCC循环的最优排气压力相同,但后者的COP优于前者。
3)采用低压级气冷器作为低压级压缩机排气的预冷器,能够有效提升DTCC循环的COP,并给出了采用低压级气冷器的DTCC循环的最优中间压力随蒸发压力和排气压力的分段函数表达式。
符号说明
COP——制冷性能系数
COPmax——最大制冷性能系数
hj——对应压焓图中各状态点(j)的制冷剂比焓值,J/kg
m——制冷剂质量流量,kg/s
pdopt,S——单级压缩最优排气压力,MPa
pdopt,D——双级压缩最优排气压力,MPa
pmopt——最优中间压力,MPa
pc——临界压力,MPa
pd——排气压力,MPa
pe——蒸发压力,MPa
pm——中间压力,MPa
Qe——制冷量,W
t2——低压级压缩机出口温度,℃
tc——临界温度,℃
tgs——气冷器中制冷剂出口温度,℃
tw——冷却水进水温度,℃
Δtsh——低压级压缩机吸气过热度,℃
V——压缩机体积流量,m3/s
W——压缩机的输入功率,W
ρ1′——低压级压缩机吸气密度,kg/m3
ηs——等熵效率
ηv——容积效率
ε——压缩比
下标
l——低压级
h——高压级

