基于热电模块实验的低温下塞贝克系数的测量
刘智博 李佳美 王世学 朱 禹
(天津大学机械工程学院 天津 300350)
随着经济的发展和人口的增长,能源需求逐年递增。天然气作为目前最清洁的化石燃料之一,是传统能源与未来可再生能源间的最佳过渡能源[1]。液化天然气(liquefied natural gas,LNG)是长途(距离≥2 000 km)运输天然气的最佳方式[2]。-162 ℃的LNG运抵气化站后,需经再气化才能输送给终端用户,再气化过程中LNG释放的冷能约为830 kJ/kg[3]。考虑LNG巨大的消耗量,若该部分冷能未被合理利用,将造成巨大浪费。为此,人们开发了多种LNG冷能的利用方式。
LNG冷能的利用方式有发电、空气分离、海水淡化等。其中,考虑到LNG气化站地理位置以及经济效益等因素,发电是回收LNG冷能的最常见方式之一[3]。传统LNG冷能发电方式是热力循环发电,但热力循环发电需要构建复杂的系统,且需要保持相对稳定的运行工况,不能灵活应对天然气供给的波动[4]。热电发电器(thermoelectric generator,TEG)基于半导体材料的塞贝克效应发电,具有无运动部件、无污染、结构简单等特点。同时,TEG仅需冷热端存在温差即可发电,可以灵活应对天然气供给的波动。因此,将TEG应用于LNG冷能发电逐渐受到人们的关注。
TEG主要由两端连接的两种不同热电材料组成:n型(带有负电荷载流子)和p型(带有正电荷载流子)半导体。通过在p、n型材料连接处施加温差产生电动势,所产生的电动势大小主要由热电材料的塞贝克系数(α)决定[5]。α是决定TEG发电性能最重要的参数之一[6],且对温度十分敏感,温度每下降30 K,Bi-Te-Sb-Se类热电材料的α减小约16%[7]。因此,将TEG应用于LNG冷能发电设计时,TEG中热电材料在低温下的α是必须的。
目前,一般商用TEG主要针对中高温余热的回收,缺乏专门针对低温冷能回收的TEG。因此,需要获得一般商用TEG中的热电材料在低温下的α,以评估已有TEG在低温下的性能并对其进行优化设计。为了对已有TEG中的热电材料进行快速测量和筛选,需要开发一种基于TEG完整模块的实验测量方法,根据该方法即可获取低温下该模块所用热电材料的α。
对于α的测量,已有学者对不同温度、不同材料进行了研究。Zhou Zhenhua等[8]将材料冷热端温差控制在1~8 K,直接测量了200~1 000 K温度范围内Co(As0.016Sb0.984)3的α,发现温度从200 K增至400 K时α从200 μV/K 增至350 μV/K。H. Werheit等[9]设计一种新的测量方法,可以有效降低系统误差对测量热电材料α的影响,并测得半导体材料YB66在100~700 K时,α随温度的升高而先增加后减小,在250 K时存在最大值约为900 μV/K。P. H. M. Böttger等[5]设计了一种稳态法测量大块样品的α和电阻率的通用仪器,得到ZnSb在温度由300 K升至450 K时α由360 μV/K增至370 μV/K,温度由450 K升至600 K时α由370 μV/K降至280 μV/K。Li Chunxiu等[10]采用经典的微分法测量了Bi2Te3材料的α,实验发现在273~573 K温度范围内,随温度升高,p型材料α先增大后减小,并在473 K存在最大值约为1.680 2×10-4V/K,n型材料α先减小后增大,在473 K时存在最小值约为-1.667 9×10-4V/K。J. De Boor等[11]开发了一种测量300~1 000 K热电材料α的系统,实验发现温度从300 K升至1 000 K时,半导体材料Cu54Ni44Mn1的α逐渐由137 μV/K增至260 μV/K。已有研究指出,温度由300 K升至350 K时热电材料Bi2Te3的α由225 μV/K增至240 μV/K[12],而当温度降至90 K时,α降至65 μV/K[7]。
上述研究表明,热电材料的α具有强温度依存性,且目前研究多是对热电材料的测量,缺少对TEG模块的直接测量方法。在实际应用中,TEG模块的制作成本高昂,破坏模块再对热电材料进行测量的代价过大。因此对于结构完整的TEG模块,给出相应的α直接测量方法是简洁而实用的。C.T.Hsu等[13]借助热阻网络分析了陶瓷、铜导流片等热阻,未分析接触热阻,测量得到以Bi2Te3为主体热电材料的TEG模块热端温度300~370 K,冷热端温差控制在20 K时的α,随着热端温度由300 K增至370 K,α由327 μV/K降至286 μV/K。张文[14]设计搭建了一款能够测试TEG物性的装置,测量了363~403 K温度范围内一款TEG模块(内含199对pn结)的α,发现随温度升高α由0.057 V/K增至0.057 5 V/K,变化幅度较小。S. Karabetoglu等[15]研究了基于Bi2Te3的TEG模块在100~375 K温度范围内的低温特性,发现随着温度由100 K升至400 K,Bi2Te3的α由86.25 μV/K增至380 μV/K。上述测量虽然是基于TEG模块进行的,但均未考虑接触热阻的存在使pn结冷热端温差的测量值大于实际值,进而导致所测α偏小的影响。
可以看出,已有研究大部分是对热电材料直接测量α,针对TEG模块测量来得到α的研究较少。少量的针对TEG模块的测量方法也并未考虑接触热阻的影响。Wang Shixue等[16]研究指出,在0.2 MPa加载压力下和80 ℃平均温度时,TEG与冷热源壁面间的接触热阻值达到9.4×10-4m2·K/W,热电模块各部分总热阻为15.7×10-4m2·K/W,可知接触热阻在TEG模块的热量传递过程中影响显著。由于低温下热电模块中pn结材料、陶瓷基板、界面材料的热阻和接触热阻的具体变化不明确,难以准确给出pn结冷热端温差。故本文借助热阻网络分析给出了一种测量低温下TEG各部分热阻(pn结、陶瓷基板、界面材料和接触热阻等)的方法,并结合开路电压的测量,获得商用TEG模块中热电材料低温下的α。该方法可为现有TEG用于低温冷能发电的设计和优化提供支持。
1 实验装置与方法
1.1 实验装置
设计并搭建了如图1所示实验系统,由液氮罐、供电段、测量仪器段、实验段组成。液氮罐为实验段提供了冷源——液氮;供电段中的调压器为TEG冷热端加热器提供可变加热功率,以便调节热电模块冷热端的温度,直流电源为压力传感器提供电压;测量仪器段主要包括用于采集数据的数据采集仪、电脑、万用表以及电子负载。实验段部分如图2所示,主要由冷端部件、被测样品、热端部件以及保温层组成。

图1 实验系统Fig.1 Experimental system

图2 实验段Fig.2 Experimental section
冷端部件主要由冷端换热器、冷端加热器和冷端不锈钢块组成。其中,冷端换热器中盛放液氮作为冷源;冷端加热器由3根额定功率为100 W的加热棒组成,插在冷端换热器底部梯形铜块上的3个直径为4 mm的通孔中,用来调节冷端温度;冷端不锈钢块紧贴在冷端换热器下表面,不锈钢块轴线由下而上等距(5 mm)布置5个直径0.6 mm、深28 mm的测温孔,利用直径为0.5 mm、精度为±0.1 K的T型热电偶测量不锈钢块轴向的温度分布。
热端部件主要由热端不锈钢块、梯形铜块、热端加热器、硅酸铝保温板、聚四氟乙烯保温板和轮辐式压力传感器组成。其中,紧贴在样品下表面的是热端不锈钢块,尺寸和作用与冷端不锈钢块相同。再下方是起热量汇聚作用的梯形铜块。铜块下方是400 W铝制加热器(100 mm×100 mm×20 mm),通过调压器控制加热功率来改变热侧温度。轮辐式压力传感器与压力加载用不锈钢圆盘靠螺纹相连后紧贴在聚四氟乙烯板下方。
为尽量减少冷量散失,选用平均厚度达到70 mm的聚氨酯保温层(0.024 W/(m·K)),同时聚氨酯与实验段间的缝隙由10 mm厚的气凝胶(0.018 W/(m·K))来填充。
实验用测量仪器及其型号、精度和量程等参数如表1所示。

表1 测量设备的型号、量程和误差Tab.1 The range and error of measuring equipments
1.2 实验方法
塞贝克系数计算式:
(1)
式中:α为塞贝克系数,μV/K;Voc为开路电压,μV;N为热电模块中pn对数量;Thot,pn为pn结的热端温度,K;Tcold,pn为pn结的冷端温度,K。
1.2.1Thot,pn和Tcold,pn的计算
为得到Tcold,pn和Thot,pn,对单个pn结进行了热阻网络分析,如图3所示。其中,不同于中高温实验中采用导热硅脂作为界面材料来减小接触热阻影响,本文选用0.5 mm石墨作为低温下的界面材料。图3(a)为实验段中TEG模块和冷热端不锈钢块局部示意图;对单个pn结放大得到图3(b),由上至下依次为石墨、陶瓷、铜导流片以及pn结;将图3(b)进行热阻分析得到图3(c);图3(d)则为对热阻网络的简化。
图3(c)中,由上至下,Rc,G-SS为石墨片和不锈钢之间的接触热阻;Rgraphite为石墨片热阻;Rc,G-C为石墨片和陶瓷之间的接触热阻;Rceramic为陶瓷热阻;Rc,Cu-C为铜导流片和陶瓷间的接触热阻;RCu为铜导流片热阻;Rc,Cu-pn为铜导流片和pn结间的接触热阻;Rp、Rn为pn结热阻。所有热阻单位均为m2·K/W。
考虑到导流片和陶瓷间有导热胶填充、导流片与pn结间有焊料填充,Rc,Cu-C和Rc,Cu-pn比Rc,G-C小很多[16-17],故忽略了Rc,Cu-C和Rc,Cu-pn。同时,RCu远小于Rp、Rn,为简化计算,将它们忽略。以往研究表明[18],相同条件下,氧化铝陶瓷表面与不锈钢表面相近,可认为Rc,G-SS和Rc,G-C相同,均为Rc,本实验中pn结冷热端温差又足够小,故冷热端情况相同。为便于实验与计算,分别将pn结冷热端热阻(包括Rc、Rgraphite、Rceramic三部分)进行合并,得到整体热阻Rsum,如图3(d)所示。

图3 单个pn结热阻网络图Fig.3 Thermal resistance network diagram of single pn junction
根据简化热阻网络分析可知,Thot,pn和Tcold,pn计算式如下:
Thot,pn=Thot,ss-qhotRsum
(2)
Tcold,pn=Tcold,ss+qcoldRsum
(3)
式中:Thot,ss为热端不锈钢上表面温度,K;Tcold,ss为冷端不锈钢下表面温度,K,二者均可根据测温点的温度拟合给出;qhot、qcold分别为根据冷热端不锈钢测温点温度计算得到的热侧和冷侧的热流密度,W/m2;Rsum为pn结冷热端整体热阻,m2·K/W。各部分计算式如下:
(4)
(5)
qhot=khotλss
(6)
qcold=kcoldλss
(7)
Rsum=Rceramic+2Rc+Rgraphite
(8)
式中:T5、T6分别为测温点5、6的温度,K;位置如图3(a)所示;δ为5、6测温点到最近的不锈钢块表面的距离,δ=2 mm;khot、kcold分别为将热端和冷端测温点温度值线性拟合得到的斜率;λss为被测温度范围内的不锈钢导热系数,W/(m·K)。
1.2.2Rsum的测量
为得到式(8)中Rsum,首先进行pn结冷热端热阻的测量实验,原理如图4所示。

图4 热阻测量原理Fig.4 Thermal resistance measurement principle
将n层石墨片和陶瓷片组合体放置在冷热源之间,则总热阻为:
(9)
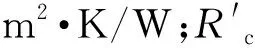

(10)
则由式(9)和式(10)得到Rsum计算公式:
Rsum=|Rm,tot-Rn,tot|/|m-n|
(11)
以n层样品为例,样品总热阻计算式如下:
(12)
流经n层样品的平均热流密度qave(W/m2),可由式(13)得到,qhot、qcold可根据式(6)、式(7)得到。
qave=(qhot+qcold)/2
(13)
1.3 误差分析
实验中各测量仪器的精度如表1所示,热流密度和塞贝克系数的相对误差计算公式为:
(14)
(15)
式中:σ表示各参数测量值的最大绝对误差;Tx、Ty分别为任意两测温点的温度,K;d为两测温点距离,mm。计算得到热流密度最大相对误差为8.85%,α的最大相对误差为3.84%。
1.4 实验系统可靠性
为检验实验的可靠性,进行重复性实验,结果如图5所示。相同工况下,多次实验结果的偏差在5%范围内。
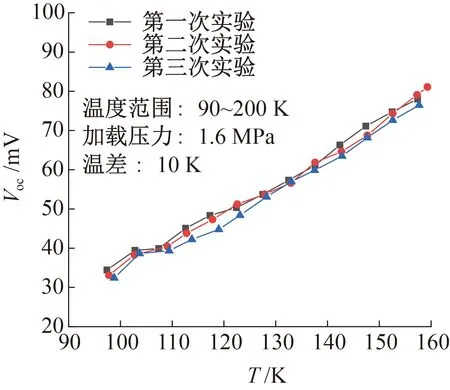
图5 低温下重复性实验结果Fig.5 Reproducible experimental results at cryogenic temperature
为进一步验证实验的可靠性,采用本实验装置对热电模块在中高温温度范围内的性能进行了测量,得到热电模块在中高温范围内的开路电压Voc。其中,对中高温范围内TEG应用的研究发现,加载压力选定为0.1~0.4 MPa[19],因此,本文选定该范围内的压力作为验证性实验的加载压力。实验测量值与厂家提供的开路电压的对比如图6所示,结果表明测量值与厂家提供的数据基本一致,最大偏差小于5%。
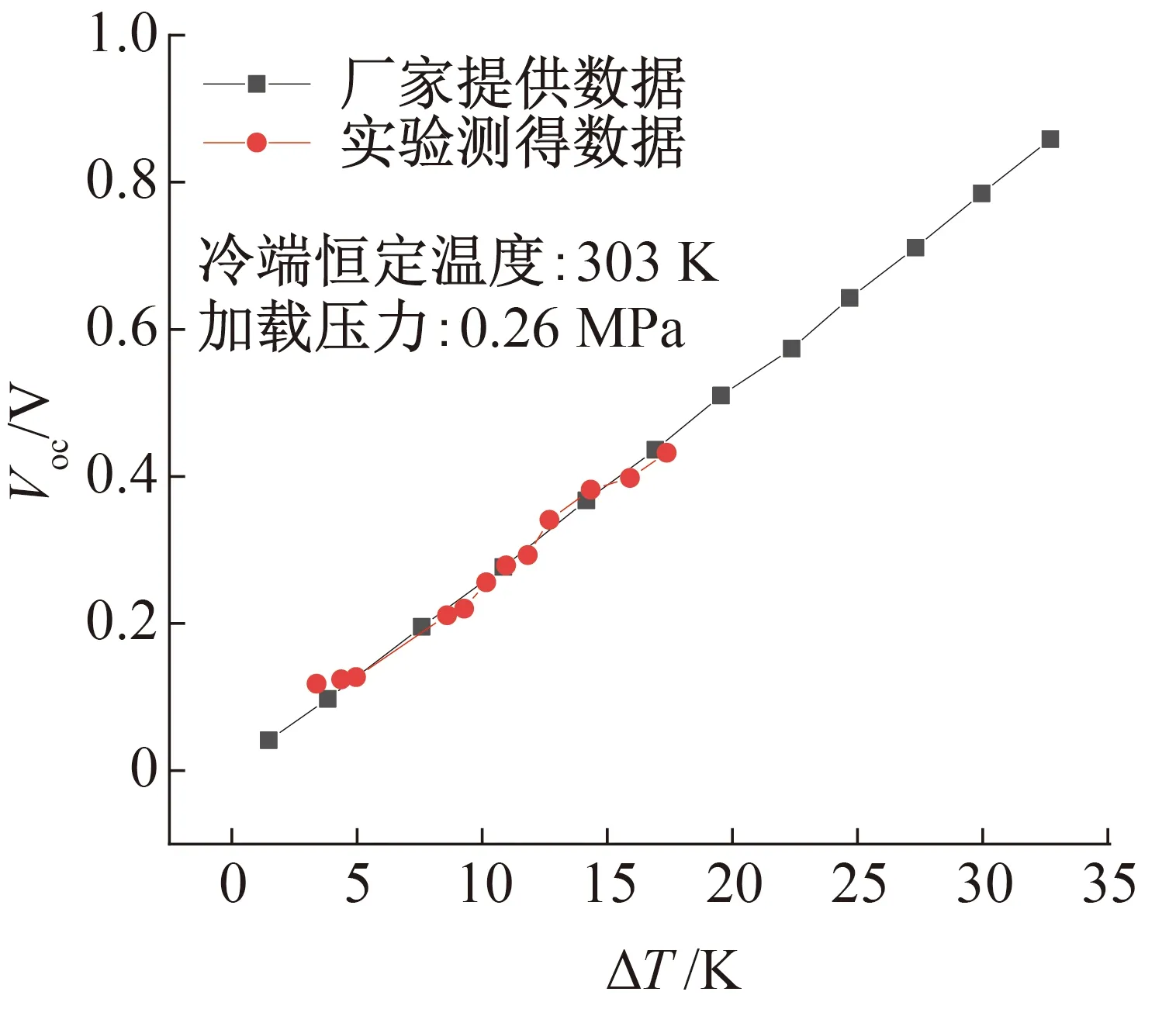
图6 常温下验证性实验结果Fig.6 Confirmatory experimental results at room temperature
2 结果与讨论
实验中为得到热电材料低温下塞贝克系数,对一款被广泛应用的TEG模块(TEHP1-12656-0.3,Thermonamic)进行了测量。该型号TEG模块以Bi2Te3固溶体合金为主体热电材料,Bi2Te3化合物及其固溶体合金是研究最早也是最成熟的适用于常温区间的热电材料。TEG模块结构如图7所示,图中:La、Wa和Ha分别为陶瓷板的长度、宽度和高度,mm;Lb、Wb和Hb分别为铜导流片的长度、宽度和高度,mm;Lc、Wc和Hc分别为pn结的长度、宽度和高度,mm。各部分详细参数如表2所示,该TEG模块包含126对pn结。

图7 热电模块结构Fig.7 Thermoelectric module structure

表2 热电模块材料尺寸参数Tab.2 Thermoelectric module material geometric dimension parameters
2.1 加载压力的确定
加载压力是决定接触热阻的主要因素,因此本文首先研究了加载压力一定时,界面温度随加载压力的变化。加载压力对温差的影响如图8所示。由图8可知,随着加载压力增加,冷热端不锈钢块的界面温差逐渐减小,且在加载压力升至1.6 MPa以后,界面温差基本保持在约10 K不变。这说明在1.6 MPa以后,加载压力对于接触热阻的影响逐渐减弱。因此本实验选定1.6 MPa作为实验的加载压力,即模块测量和热阻测量均在该压力下进行。

图8 加载压力对温差的影响Fig.8 Effect of loading pressure on temperature difference
2.2 塞贝克系数的测量
为了计算热电模块塞贝克系数,首先进行了整体热阻的测量,并使相关测量条件(0.5 mm石墨片、1.6 MPa压力、温度区间等)与热电模块测量时相同,结果如图9所示。整体热阻Rsum随温度的升高而降低,Rsum在93 K时存在最大值4.2×10-4m2·K/W,在180 K时存在最小值1.7×10-4m2·K/W。由于在90~180 K温度范围内,压力和界面材料一定时,随温度升高,石墨片、陶瓷和不锈钢的硬度发生变化,各界面间不连续的点接触面积增大,接触热阻Rc减小。已有研究表明,在90~180 K温度范围内,Rgraphite随温度变化较小[20],Rceramic随温度升高而增大[21],整体热阻Rsum随温度升高而减小主要受Rc的影响。由此可知,低温下接触热阻对整体热阻的影响较大。

图9 整体热阻测量结果Fig.9 Overall thermal resistance measurement results
根据Thot,pn和Tcold,pn的计算式,将各温度下整体热阻代入其中,得到各温度区间下pn结上的冷热端温度,结果如图10所示。pn结冷热端温差基本均为4~6 K左右,冷热端不锈钢表面间的温差则高达7~11 K,差异约为50%。这表明整体热阻对于α的测量有很大影响,必须予以考虑。

图10 pn结冷热端温度测量结果Fig.10 Temperature measurement results of the hot and cold side of the pn junction
测得开路电压Voc和pn结冷热端温差后,由式(1)可得低温下热电材料塞贝克系数随温度的变化,如图11所示。当温度由180 K降至90 K时,α由124.6 μV/K降至49.3 μV/K。由此可知,温度的降低将导致α的锐减,这也印证了半导体材料发电性能对温度的强依赖性。

图11 常温与低温区间内热电模块塞贝克系数对比Fig.11 Comparison of Seebeck coefficients of thermoelectric modules between room temperature and low temperature
此外,将实验测得的中高温下TEG模块的α也表示于图11中。可知TEG模块的α在低温区间与常温区间内均随温度的升高而增大,但低温区间内的数值远小于常温下的数值。常温区间内模块的α可达200~300 μV/K,低温区间内的α仅为49.3~124.6 μV/K。由此可知,不同温度范围内α差异较大,当热电模块在低温区间内使用时,不能直接将常温下的α用于低温下TEG的设计中,而需要使用低温下热电模块的α。
最后,为了便于工程上预测以n型和p型Bi2Te3固溶体合金为主体材料的TEG模块在低温下的发电性能,根据实验测量结果给出了低温条件下α关于温度的函数关系式:
α=0.003 07T2+0.073 43T+14.439 9
(16)
3 结论
本文提出一种在低温下测量完整TEG模块中热电材料的塞贝克系数的测量方法,即借助热阻网络分析得到TEG模块中pn结冷热端的精确温差,再结合TEG的开路电压,得到该模块低温下的塞贝克系数。并对广泛应用的以n型和p型Bi2Te3固溶体合金为主体材料的TEG模块进行了测量,得到结论如下:
1)测试结果表明常温范围内TEG热电材料塞贝克系数的测量值与厂家提供的参照值一致,证明提出的测试方法有效。
2)在90~180 K温度范围内,以n型和p型Bi2Te3固溶体合金为主体材料的TEG模块,其塞贝克系数随温度升高而增大,数值为49.3~124.6 μV/K,明显低于该TEG模块在中高温范围内的塞贝克系数200~300 μV/K。

