DP780高强钢U形弯曲回弹影响因素及优化

丁华锋，潘俊杰，晏洋，金先志，李红兵，胡泽奇，周昌钰

DP780高强钢U形弯曲回弹影响因素及优化

丁华锋1,2，潘俊杰1，晏洋2，金先志1，李红兵1，胡泽奇1，周昌钰1

（1.湖北文理学院 汽车与交通工程学院，湖北 襄阳，441053；2.湖北三环锻造有限公司，湖北 襄阳，441700）

研究DP780高强钢不同参数对其U形弯曲回弹的影响。在室温下对DP780钢板材进行拉伸试验，获得其应力应变曲线。采用U形弯曲模具模型，利用ABAQUS有限元仿真软件对U形弯曲回弹进行分析，研究摩擦因数、压边力、冲压速度和凹凸模间隙对U形弯曲回弹的影响规律，并在此基础上设计正交试验以优化影响参数。在较小的摩擦因数下，回弹是有微小波动的，继续增大摩擦因数，回弹呈现减小的趋势；回弹随着压边力的增大先增大后减小；冲压速度的改变对回弹的影响不是很大；随着凹凸模间隙的增加，回弹逐渐增大。通过正交试验得到4个参数对回弹程度的影响，最佳参数组合为5531，以此参数组合得出的侧壁角1和法兰角2最接近90°，回弹效果最好。

DP780高强钢；U形弯曲回弹；有限元仿真；正交试验

国际钢铁协会将屈服强度在210～550 MPa范围内的钢定义为高强度钢，高强钢不仅具有较高的抗拉强度，而且在汽车的轻量化、碰撞吸能和成形性等方面都有很好的实用性，这些优异的性能使其在现代汽车上得到了广泛的应用[1-2]。采用试验方法研究U形弯曲回弹影响因素具有成本高、效率低的优点，随着计算机和数值计算方法的快速发展，有限元仿真成为一种解决实际问题的有效手段，有限元仿真法成本低、周期短，在预测回弹问题方面快速发展，对汽车工业中冲压成形具有一定的指导意义[3]。

为了响应国家节能减排的政策，大量汽车开始使用高强度钢板，但是高强度钢板冲压成形过程中的回弹问题明显，回弹问题不仅是实际生产中需要解决的问题，也是学术界研究的难点和热点[4]。Xu等[5]分别研究了积分点、空白网格尺寸数、阻尼值和冲孔速度等几个参数对回弹模拟精度和效率的影响，并提出了合理的取值。Lawanwong等[6]研究了消除高强度钢板U形回弹的两种方式，通过控制法兰外冲头行程和模具中的上推力来获得理想的U形弯曲零件。Mulidrán等[7]通过模具设计方法达到了减小高强度钢回弹的目的，并将回弹预测结果与试验值进行了比较。Cui等[8]分析了电磁力对回弹标定的影响，发现较高的放电电压可以显著降低回弹，其仿真结果具有较高的精度。Spathopoulos等[9]根据回弹的影响因素提出了一种用于板材成形过程回弹预测的新型神经网络系统，并对类似工业研究中使用的测试用例进行了验证。吕琳等[10]利用有限元软件对纵弧棱U型梁进行了数值模拟，研究了压边力和摩擦因数对回弹的影响规律。聂昕等[11]通过自行设计制造的回弹试验模具研究了3种不同性能的高强度钢板在不同U形弯曲成形的冲压工艺及不同成形状态下的回弹规律。余海燕等[12]研究了两种材料U形回弹随时间而改变的时效回弹行为，其时效回弹量均可用指数函数来表达。李国栋等[13]基于2种磁脉冲辅助成形方案，揭示了铝合金板材磁脉冲辅助弯曲成形对回弹的影响机理。胡大超等[14]利用ABAQUS有限元分析，对大型U形板材工件渐进滚弯成形及其回弹过程进行了数值模拟，发现用渐进滚弯方法成形加工半椭圆形工件是可行的。文中基于ABAQUS有限元分析，对DP780高强钢U形件进行数值模拟，模型采用U形弯曲模具尺寸，研究4种不同参数的取值对回弹的影响。在此前提下，通过正交试验选出一组合理取值，使其回弹最小。

1 U形件有限元模型

1.1 拉伸试验

试验材料为宝钢集团生产的冷轧DP780钢板材，按照《金属材料拉伸试验第1部分：室温试验方法》（GB/T 228.1—2010）[15]，设计出尺寸形状如图1，厚度为2 mm的试件。在室温条件下通过微机控制电子万能试验机进行静态拉伸试验，设置拉伸速度为0.5 mm/min，试件拉伸断裂后的状态如图2所示。通过对比分析，选取其中一组试验数据处理后得到DP780钢材料的工程应力应变曲线，经公式（1）转换得到的应力应变曲线如图3所示。通过静态拉伸试验得到DP780高强钢的屈服强度为526 MPa，抗拉强度为837 MPa，密度为7.9 g·cm‒3，弹性模量为2.1×105Mpa，泊松比为0.3，伸长率为19.84%。

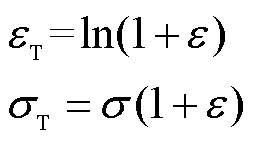
式中：ε为工程应变；σ为工程应力；εT为真实应变；σT为真实应力。

图2 试件拉伸断裂图

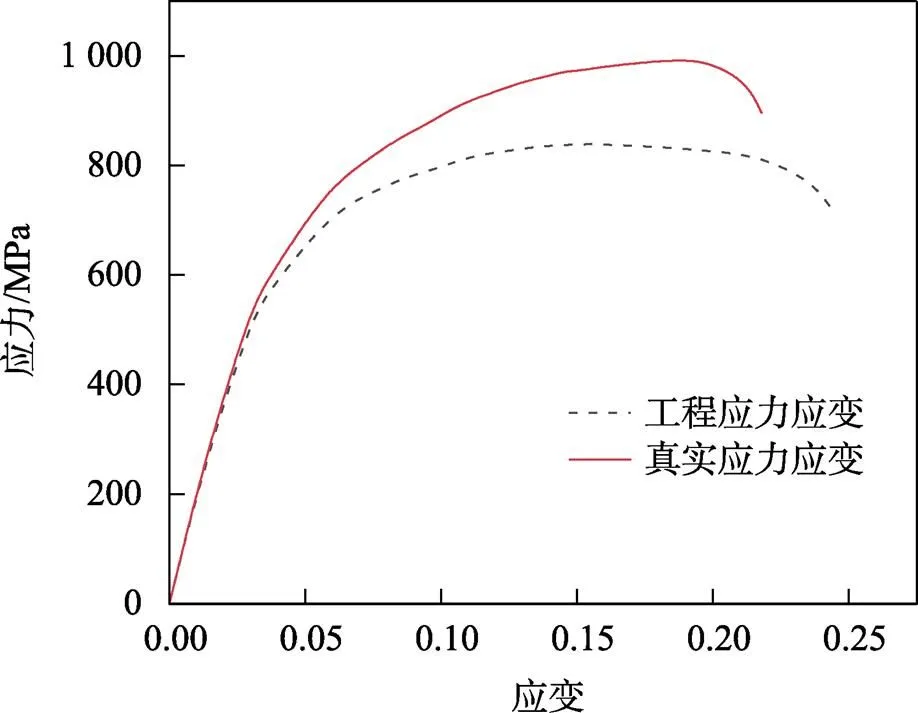
图3 应力应变曲线

1.2 U形件有限元模型的建立

U形件模具发展至今，国内外研究人员使用不同的U形弯曲模具进行了回弹分析，研究了各种影响回弹的因素和减小回弹的方法，通过试验和有限元方法对U形弯曲回弹进行了归纳和总结，为U形模具设计和实际生产提供了依据。文中采用的U形弯曲模具尺寸如图4所示，试件的尺寸为1 mm´50 mm´300 mm，由于模型是对称图形，取模型的1/2在ABAQUS中采用三维可变形壳拉伸命令画出凸模、凹模、压边圈和试件，材料属性按毫米单位制换算输入密度、杨氏模量和泊松比，试件材料塑性参数输入从屈服点到抗拉强度一段所有点，进行装配画网格后如图5所示。在分析步处设置重启动分析，各个部件之间解除部位摩擦因数均取0.1，凸模、压边圈和凹模可看做刚体，在一半模型上设置压边力为50 kN，虚拟冲压速度为1 m·s‒1。ABAQUS有限元分析一般有显示和隐式两种算法，冲压过程采用动力显示算法，回弹过程采用静力隐式算法。

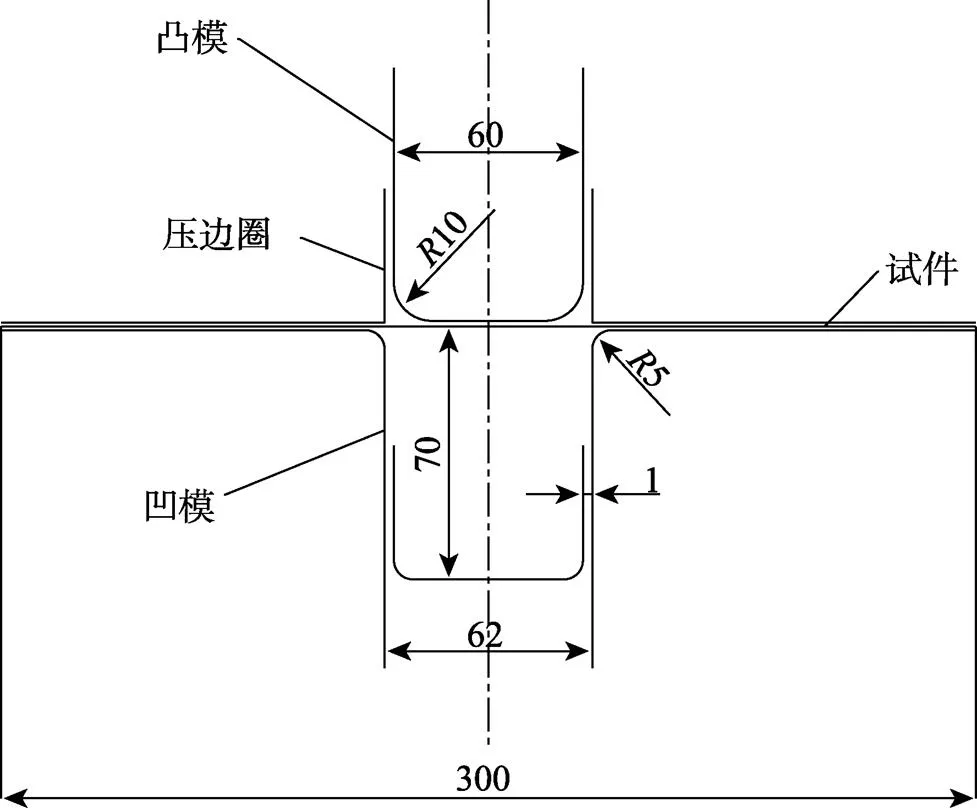
图4 U形弯曲模型尺寸图（单位：mm）

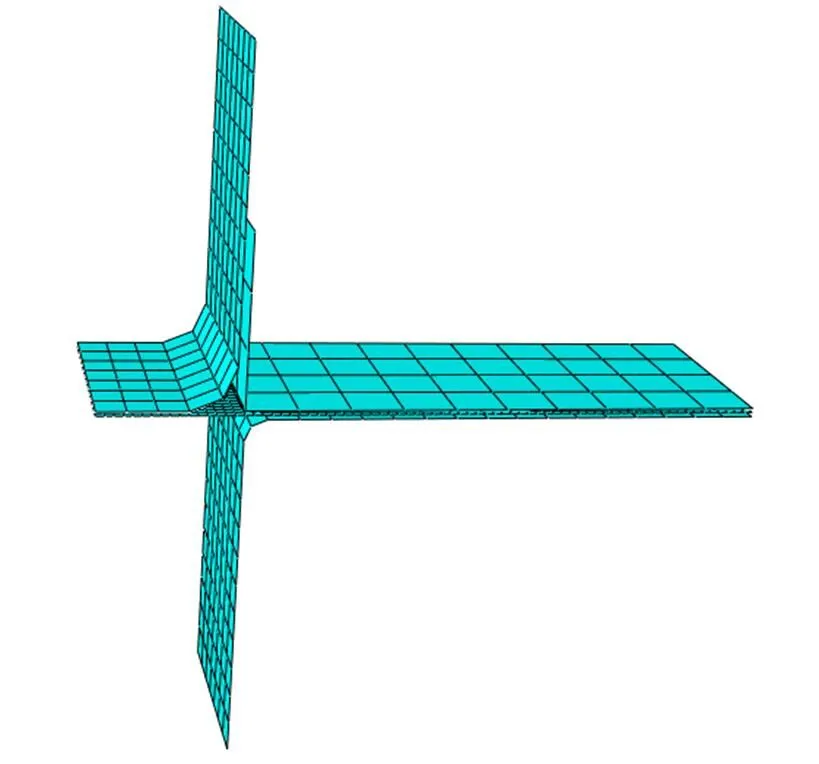
图5 1/2 U形网格模型

2 回弹测量标准与影响因素

2.1 回弹测量标准

图6为回弹测量标准，用侧壁角1和法兰角2来表示回弹的大小。回弹模拟的影响因素很多，文中只对几个显著参数进行分析。厚度积分点取7、网格尺寸大小为2[16]，在压边力为100 kN、摩擦因数为0.1、凸凹模间隙为1 mm、冲压速度为1 m/s的条件下，模拟回弹前后的三维结果和前端面结果如图7、图8所示。

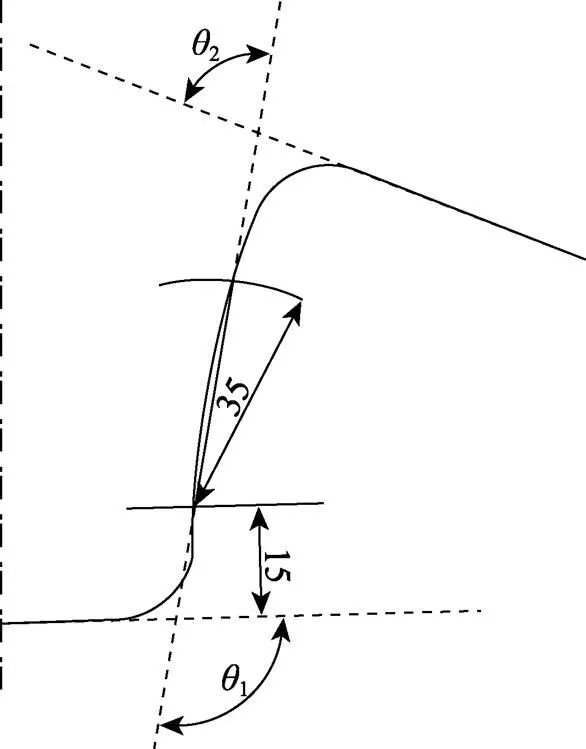
图6 回弹测量标准（单位：mm）

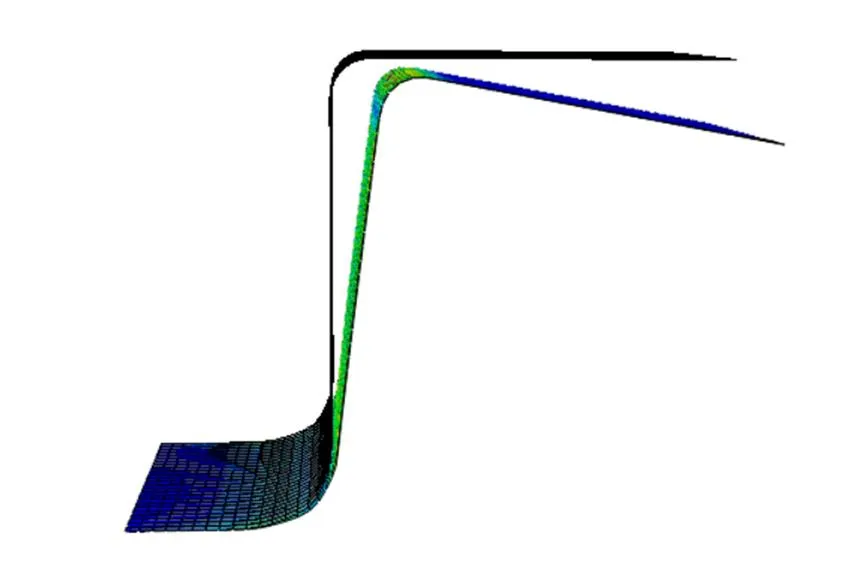
图7 模拟回弹前后结果

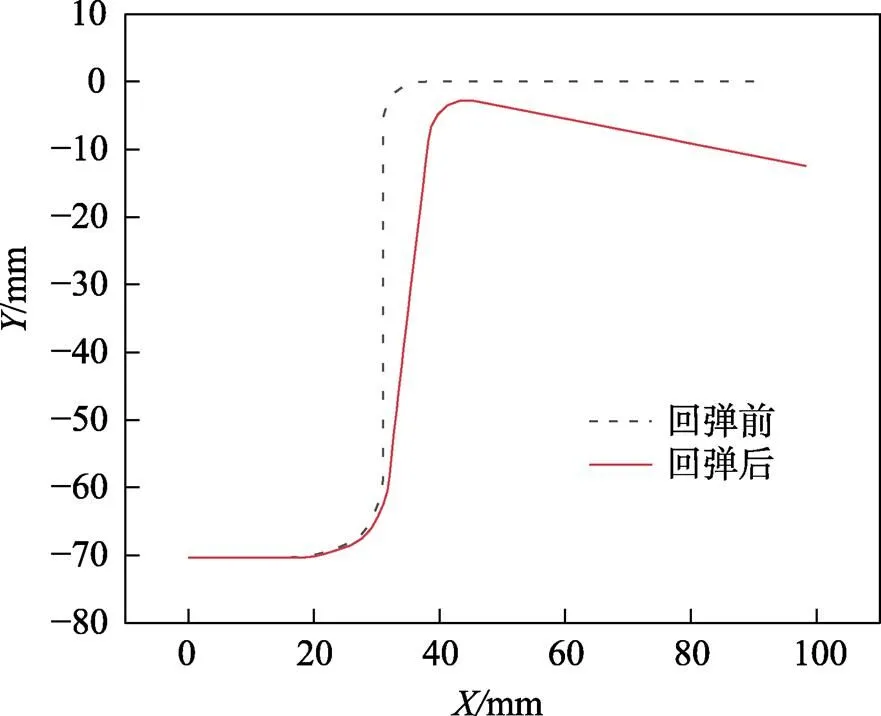
图8 前端面回弹结果

2.2 摩擦因数对回弹的影响

在其他条件不变的情况下，仅改变摩擦因数取值对回弹的影响如图9、图10所示。在较小的摩擦因数下，其回弹有微小的波动，继续增大摩擦因数，回弹量呈现减小的趋势，这一规律与孙伟等[17]和薛克敏等[18]得出的结论相同。当摩擦因数较小时，板料在冲压过程流动越容易，回弹越小，再选择较大的摩擦因数会减小回弹，摩擦因数的增大对法兰角2的影响较大，压边圈与凹模之间的摩擦力变大，使两个材料表面之间的流动阻力增大，经过模具脱离后回弹减小，但较大的摩擦因数对材料的成形质量有影响，可能出现拉裂危险。

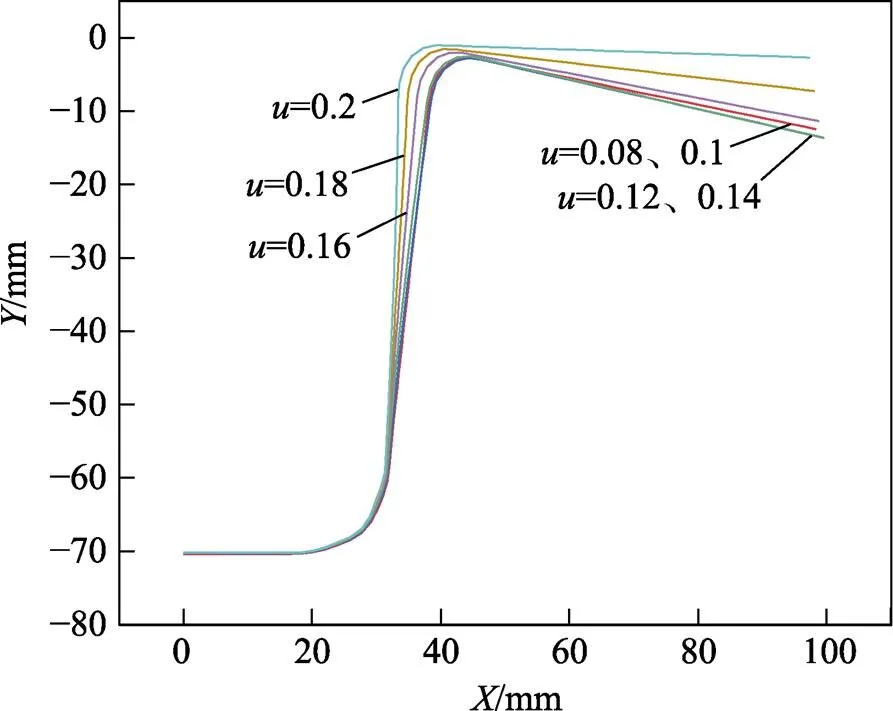
图9 不同摩擦因数下的回弹大小

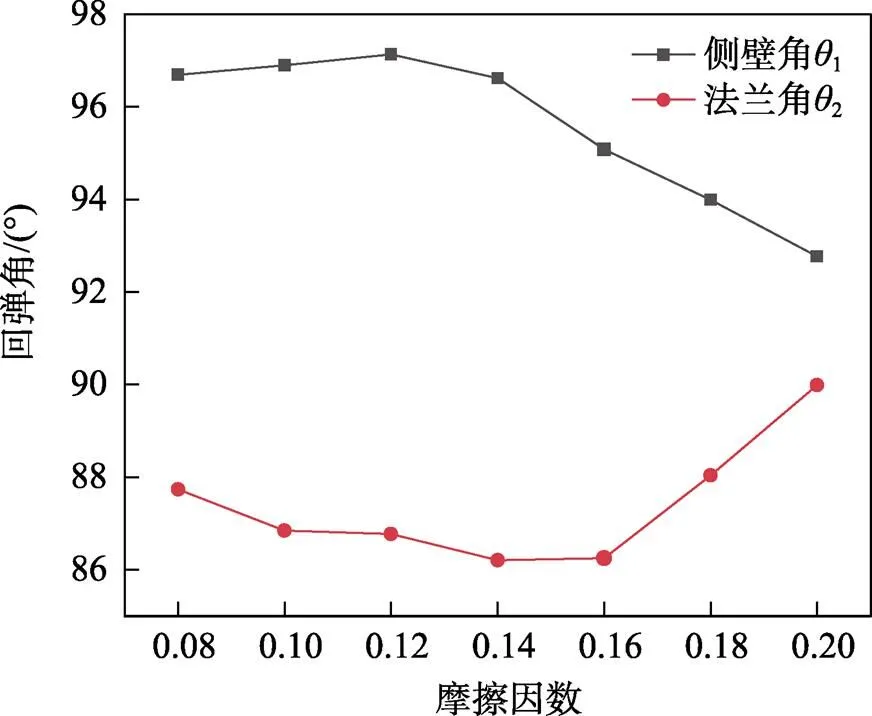
图10 摩擦因数对回弹影响

2.3 压边力对回弹的影响

不同压边力取值对回弹的影响如图11、图12所示。在压边力较小的情况下，回弹先随着压边力的增大而增大，之后又随着压边力的增大而减小，这与张华平等[19]和张茜等[20]得出的结论一致。较大的压边力对侧壁角1的影响较大，在压边圈压紧状态下进行冲压过程会使材料侧壁产生严重的塑性变形，也导致材料侧壁的减薄率增大，最终对侧壁角的回弹产生较大影响，从而影响装配尺寸精度。

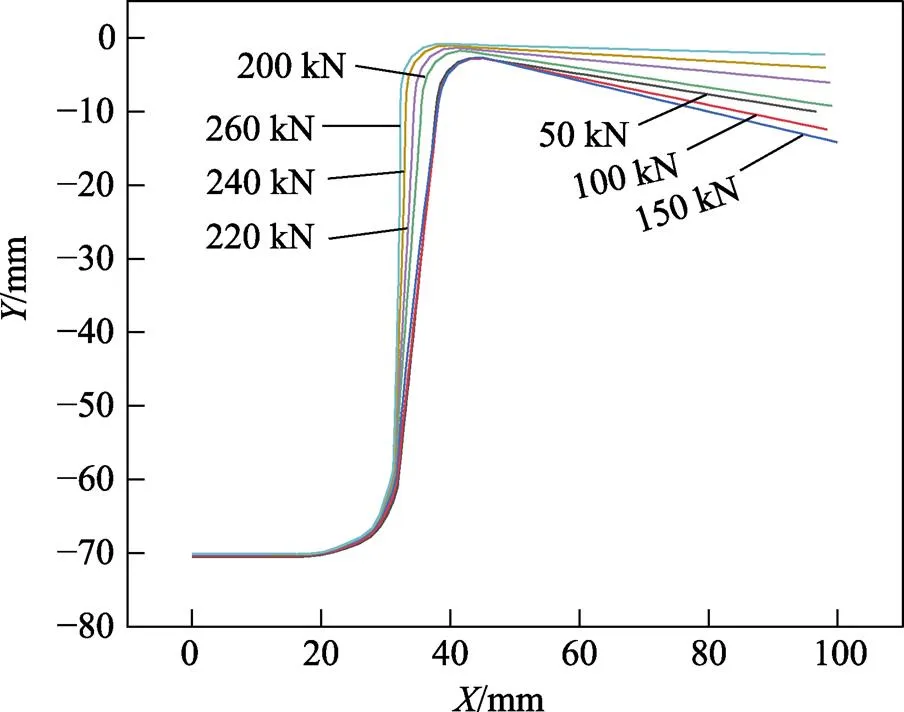
图11 不同压边力下回弹的大小

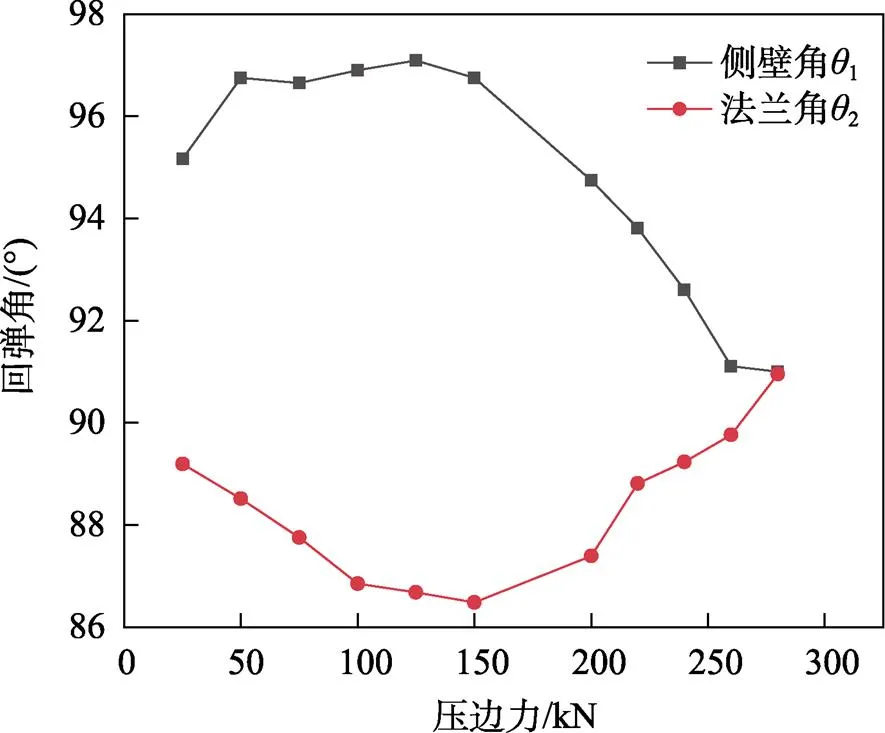
图12 压边力对回弹的影响

2.4 冲压速度对回弹的影响

不同的冲压速度对回弹的影响如图13、图14所示。可以看出，冲压速度的改变对回弹的影响不是很大，这与郑淇文等[21]得到的结果相同。模拟过程中不同的冲压速度对运算的快慢有很大的影响，冲压成形过程中较大的速度对模具磨损有较大的影响，回弹是板料在模具卸载后的变化量大小，冲压速度的改变对最终回弹影响不大。

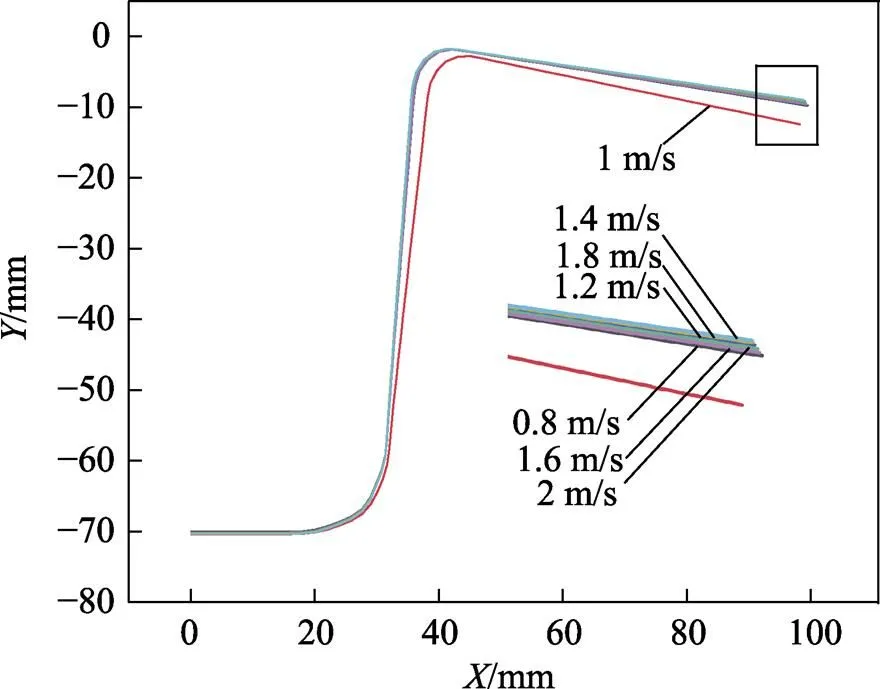
图13 不同冲压速度下回弹的大小

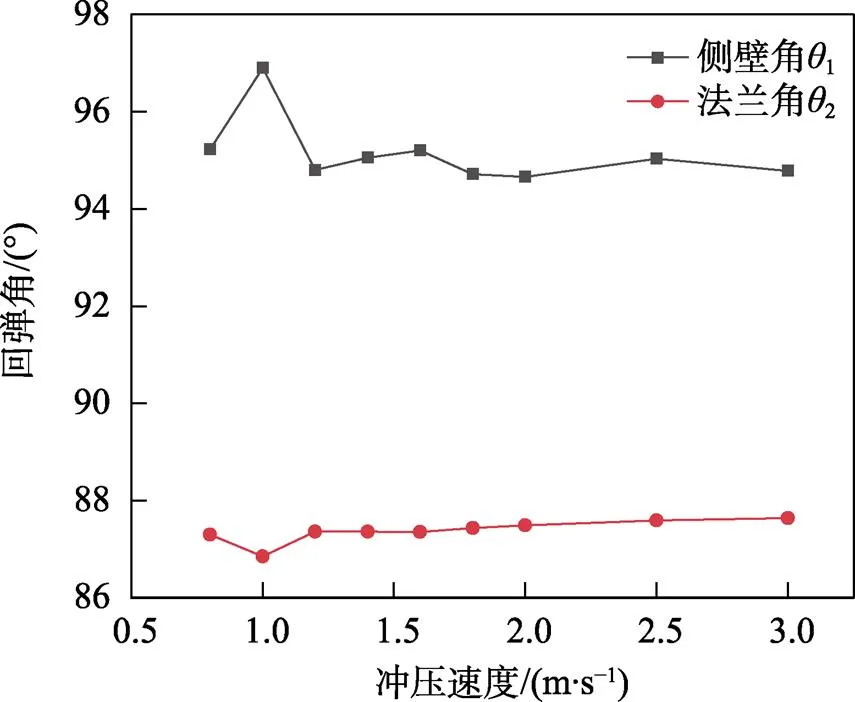
图14 冲压速度对回弹的影响

2.5 凹凸模间隙对回弹的影响

不同凹凸模间隙对回弹的影响如图15、图16所示。随着凹凸模间隙的增大，回弹在逐渐增大，这与钟文等[22]和吴信涛等[23]的结论相同。厚度与间隙值相同时，主要是凸模和凹模圆角处发生回弹，在侧壁处基本没有大的弯曲回弹现象；间隙一旦超过其厚度后，在冲压侧壁产生一定的弯曲回弹，用曲率半径来表示回弹大小，间隙值继续增加到一定程度，则产生更大的回弹，曲率半径越小，回弹越明显。

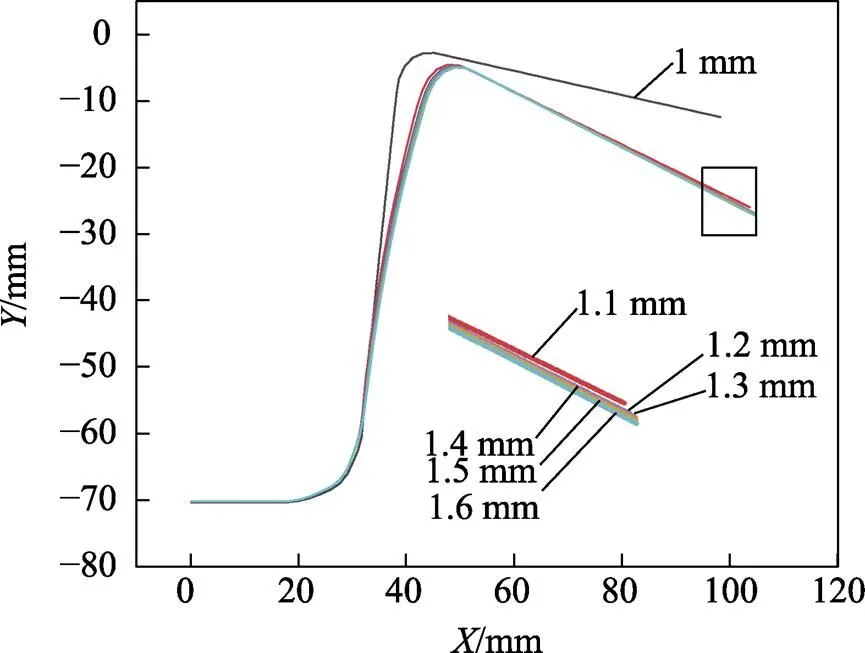
图15 不同凹凸模间隙下回弹的大小

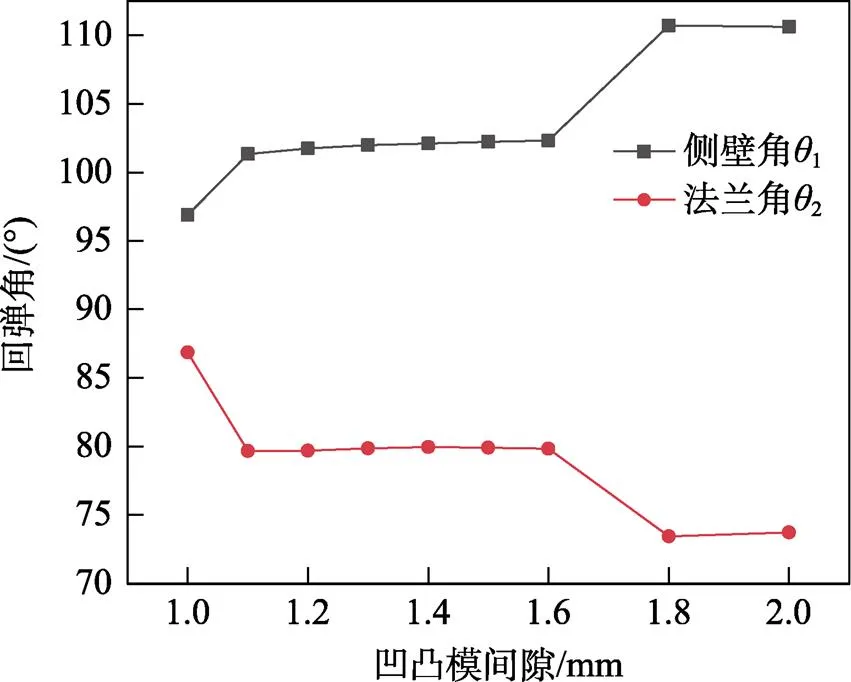
图16 不同凹凸模间隙对回弹的影响

3 正交试验

3.1 正交试验表设计

上述通过研究不同摩擦因数、压边力、冲压速度和凹凸模间隙单个因素对U形弯曲回弹的影响，并与其他文献结果对比，验证了文中模拟过程的准确性。更进一步地，采用正交试验分析这4个参数及各参数取值对回弹的影响程度。正交试验是一种研究多因素多水平的设计方法，可以提高优化效率、减少有限元模拟次数，正交表具有正交性、均匀分散性和整齐性等特点，能够通过较少的试验次数找出每个因素的影响大小，确定出最佳参数组合[24]。在试验过程中使用四因素五水平(L25(45))的正交试验表，基于单因素对回弹的影响选取一些比较具有代表性的水平参数进行模拟，各因素之间无交互作用，回弹考核指标为侧壁角1和法兰角2越接近90°越好，正交试验表如表1所示。

表1 影响回弹指标的因素和水平

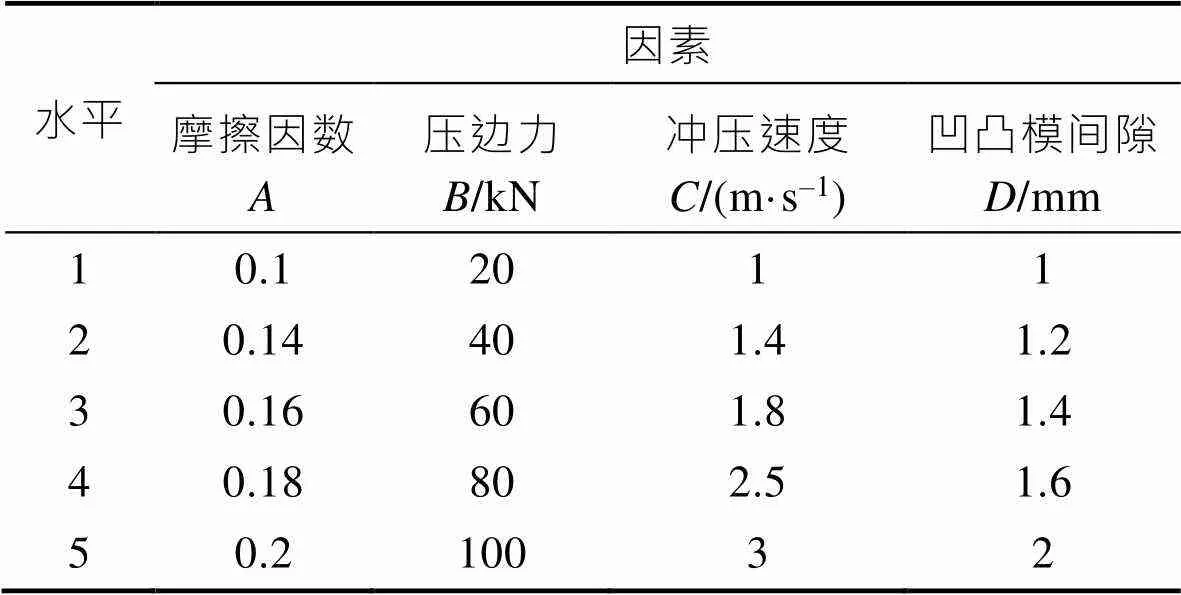
Tab.1 Factors and levels affecting the springback index

3.2 正交试验结果分析

表2为四因素五水平正交表得出的25组试验数据结果，表3、表4是侧壁角1和法兰角2的极差分析结果，其中，1、2、3、4、5分别表示各因素不同水平对应的指标均值，并用各均值的最大值减去最小值，求出各因子的极差，以确定各因素对回弹影响程度的大小。可以看出，侧壁角1和法兰角22个极差的影响因素大小都相同，均为凹凸模间隙＞摩擦因数＞冲压速度＞压边力，回弹最小的最佳参数组合为5531，以此参数组合（试验号25）得出的侧壁角1和法兰角2最接近90°，回弹效果最好。

表2 L25(45)正交试验结果

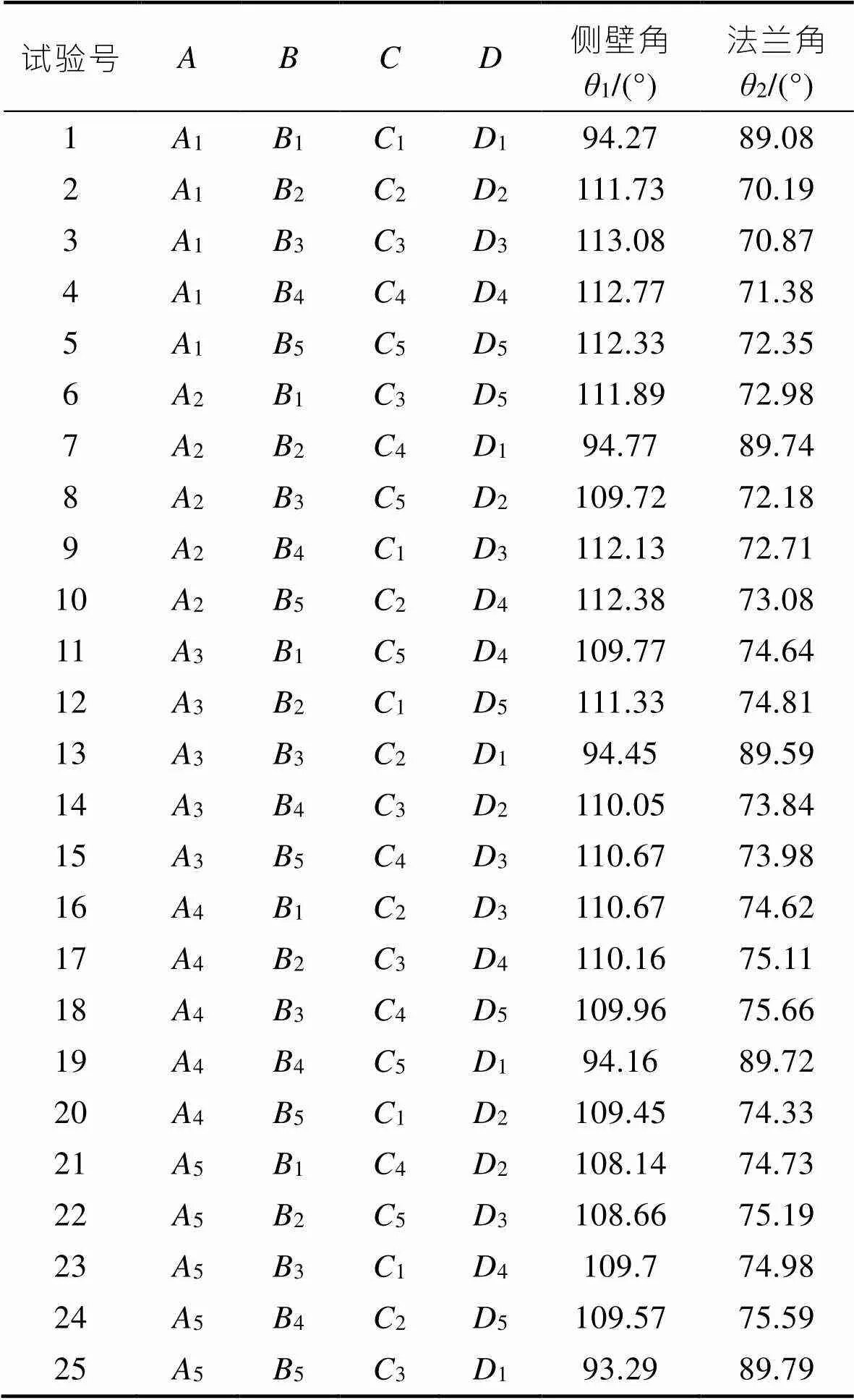
Tab.2 L25 (45) orthogonal test results

表3 侧壁角1极差分析

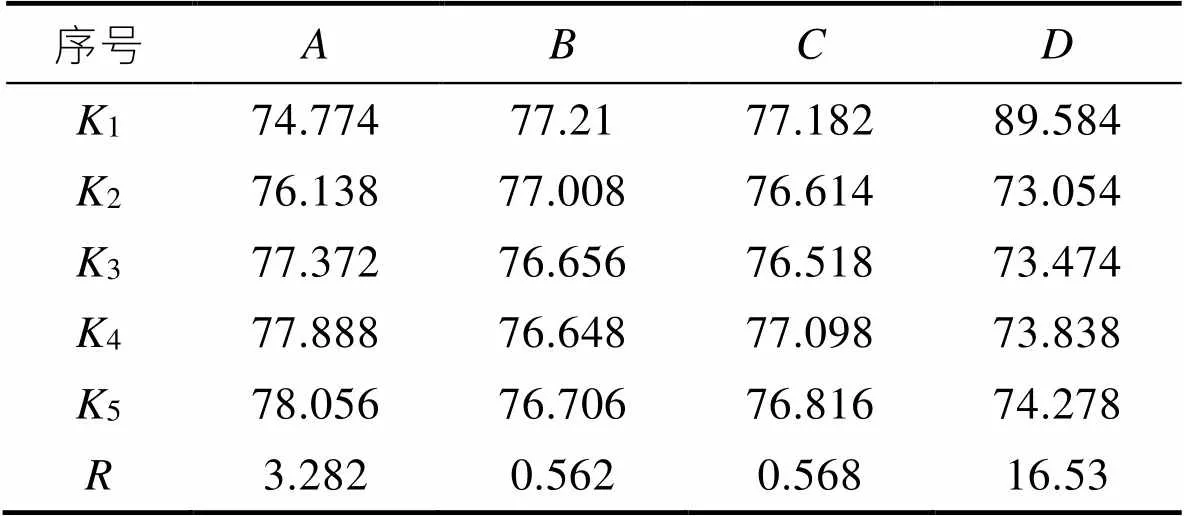
Tab.3 Range analysis of side wall angle θ1

表4 法兰角2极差分析

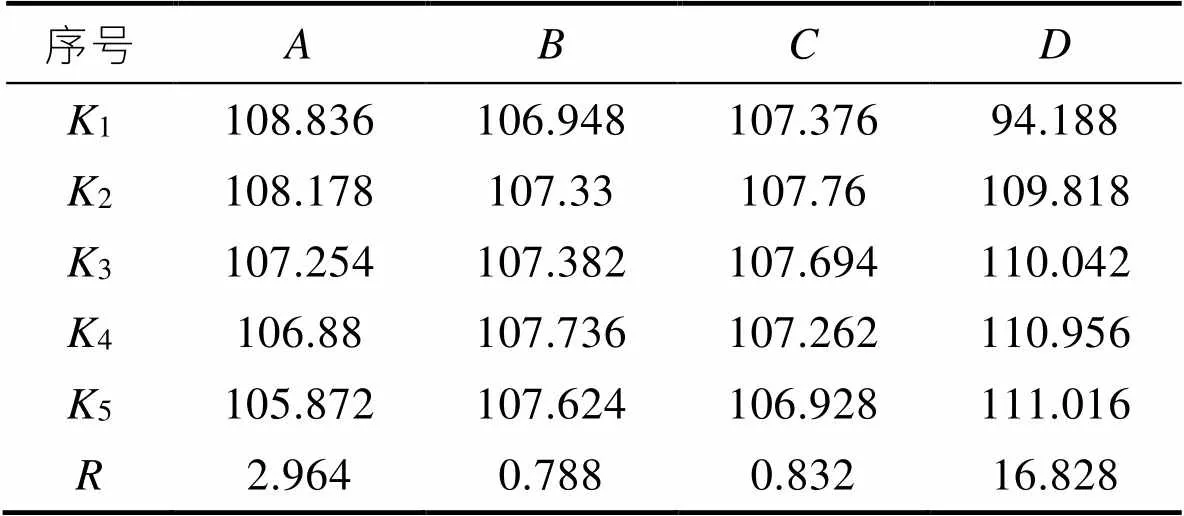
Tab.4 Range analysis of flange angle θ2

4 结论

1）利用ABAQUS有限元分析研究DP780高强钢U形弯曲回弹影响因素，发现在其他参数不变的情况下，摩擦因数较小时，其回弹是有微小波动的，继续增大摩擦因数，回弹呈现减小的趋势；回弹随着压边力的增大先增大后减小冲压速度的改变对回弹的影响不是很大；随着凹凸模间隙增大，回弹在逐渐增大。

2）通过正交试验并采用极差分析，得出侧壁角1和法兰角2的影响因素大小都相同，即对回弹的影响从大到小排序是凹凸模间隙＞摩擦因数＞冲压速度＞压边力。回弹最小的最佳参数组合为5531，以此参数组合得出的侧壁角1和法兰角2最接近90°，回弹效果最好。

[1] 罗培锋, 杨万庆, 陈东, 等. 高强度钢成形技术及车身轻量化应用[J]. 汽车实用技术, 2020, 45(16): 170-175.

LUO Pei-feng, YANG Wan-qing, CHEN Dong, et al. Forming Technology of High Strength Steel and Application of Body Lightweight[J]. Automobile Applied Technology, 2020, 45(16): 170-175.

[2] 潘利波, 祝洪川, 魏星. 车身用高强钢的回弹实验与分析[J]. 精密成形工程, 2019, 11(1): 25-29.

PAN Li-bo, ZHU Hong-chuan, WEI Xing. Test and Analysis on Springback of High Strength Steel for Car Body[J]. Journal of Netshape Forming Engineering, 2019, 11(1): 25-29.

[3] 李富柱, 翟长盼, 李伟, 等. 汽车车身构件冲压回弹研究现状[J]. 锻压技术, 2018, 43(2): 1-8.

LI Fu-zhu, ZHAI Chang-pan, LI Wei, et al. Research on Status of Stamping Springback for Auto-Body Parts[J]. Forging & Stamping Technology, 2018, 43(2): 1-8.

[4] 吴向东, 张毅升, 万敏, 等. 板材成形性能试验方法及应用[J]. 精密成形工程, 2019, 11(3): 42-50.

WU Xiang-dong, ZHANG Yi-sheng, WAN Min, et al. Application and Test Methods of Sheet Metal Formability[J]. Journal of Netshape Forming Engineering, 2019, 11(3): 42-50.

[5] XU W L, MA C H, LI C H, et al. Sensitive Factors in Springback Simulation for Sheet Metal Forming[J]. Journal of Materials Processing Technology, 2004, 151(1-3): 217-222.

[6] LAWANWONG K, HAMASAKI H, HINO R, et al. Double-Action Bending for Eliminating Springback in Hat-Shaped Bending of Advanced High-Strength Steel Sheet[J]. The International Journal of Advanced Manufacturing Technology, 2020, 106(5): 1855-1867.

[7] MULIDRÁN P, SPIŠÁK E, TOMÁŠ M, et al. Numerical Prediction and Reduction of Hat-Shaped Part Springback Made of Dual-Phase AHSS Steel[J]. Metals, 2020, 10(9): 1119.

[8] CUI Xiao-hui, ZHANG Zhi-wu, YU Hai-liang, et al. Springback Calibration of a U-Shaped Electromagnetic Impulse Forming Process[J]. Metals, 2019, 9(5): 603.

[9] SPATHOPOULOS S C, STAVROULAKIS G E. Springback Prediction in Sheet Metal Forming, Based on Finite Element Analysis and Artificial Neural Network Approach[J]. Applied Mechanics, 2020, 1(2): 97-110.

[10] 吕琳, 刘武静, 高红兰. 纵弧棱U型梁的冲压回弹预测[J]. 塑性工程学报, 2021, 28(5): 211-217.

LÜ Lin, LIU Wu-jing, GAO Hong-lan. Prediction of Stamping Springback of Longitudinal Arc Rib U-Shaped Beam[J]. Journal of Plasticity Engineering, 2021, 28(5): 211-217.

[11] 聂昕, 杨昕宇, 牛星辉, 等. 基于不同U形弯曲冲压工艺的高强度钢板回弹实验研究[J]. 锻压技术, 2019, 44(12): 1-10.

NIE Xin, YANG Xin-yu, NIU Xing-hui, et al. Experimental Study on Springback of High Strength Steel Sheet Based on Stamping Processes under Different U-Shaped Bending[J]. Forging & Stamping Technology, 2019, 44(12): 1-10.

[12] 余海燕, 吴航宇, 汪林. 先进高强钢板冲压成形后的时效回弹行为[J]. 塑性工程学报, 2021, 28(6): 2-7.

YU Hai-yan, WU Hang-yu, WANG Lin. Time-Depe­ndent Springback Behavior of Advanced High Strength Steel Sheet after Stamping Forming[J]. Journal of Plasticity Engineering, 2021, 28(6): 2-7.

[13] 李国栋, 黄亮, 李建军, 等. 铝合金板材磁脉冲辅助U形弯曲过程回弹数值模拟分析[J]. 精密成形工程, 2018, 10(1): 148-155.

LI Guo-dong, HUANG Liang, LI Jian-jun, et al. Numerical Simulation of Springback Analysis for Electromagnetic Assisted U-Shaped Bending of Aluminum Alloy Sheet[J]. Journal of Netshape Forming Engineering, 2018, 10(1): 148-155.

[14] 胡大超, 李国庆, 付泽民. 大型U形板材工件渐进滚弯成形数值模拟[J]. 精密成形工程, 2011, 3(6): 117-120, 125.

HU Da-chao, LI Guo-qing, FU Ze-min. Numerical Sim­u­­­lation of Multiple-Step Roll-Bending Forming of Large-Scale Sheet Metal with U Shape[J]. Journal of Netshape Forming Engineering, 2011, 3(6): 117-120, 125.

[15] 国家质量监督检验检疫总局, 中国国家标准化管理委员会. 金属材料拉伸试验第1部分：室温试验方法: GB/T 228.1—2010[S]. 北京: 中国标准出版社, 2011.

General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Metallic Materials-Tensile Testing-Part 1: Method of Test at Room Temperature: GB/T 228.1— 2010[S]. Beijing: Standards Press of China, 2011.

[16] 徐伟力, 马朝晖, 李川海, 等. 回弹显式解法的影响因素[J]. 锻压技术, 2004, 29(6): 12-15.

XU We-li MA Chao-hui, LI Chuan-hai et al. Effecting Factors on Solution of Springback Simulation[J]. Forging & Stamping Technology, 2004, 29(6): 12-15.

[17] 孙伟, 王岩松, 赵礼辉, 等. 基于响应面法的DP600高强钢U型件冲压拉延回弹变形研究[J]. 热加工工艺, 2018, 47(23): 115-120.

SUN Wei, WANG Yan-song, ZHAO Li-hui, et al. Research on Drawing Springback Deformation of DP600 High Strength Steel U-Shaped Parts Based on Response Surface Method[J]. Hot Working Technology, 2018, 47(23): 115-120.

[18] 薛克敏, 陈龙, 孔炎, 等. CLAM钢U形弯曲回弹数值模拟优化与试验[J]. 塑性工程学报, 2013, 20(1): 53-57.

XUE Ke-min, CHEN Long, KONG Yan, et al. Numerical Simulation Optimization and Experimental Study on U-Bending Springback of CLAM Steel[J]. Journal of Plasticity Engineering, 2013, 20(1): 53-57.

[19] 张华平, 李亚, 连昌伟. DP980高强钢U形弯曲实验与数值模拟[J]. 锻压技术, 2020, 45(4): 70-75.

ZHANG Hua-ping, LI Ya, LIAN Chang-wei. Test and Numerical Simulation of U-Shape Bending Part for DP980 High Strength Steel[J]. Forging & Stamping Technology, 2020, 45(4): 70-75.

[20] 张茜, 刘淑影, 牛星辉, 等. 基于Dynaform的DP600高强钢U形弯曲回弹影响因素研究[J]. 模具制造, 2020, 20(4): 32-35.

ZHANG Qian, LIU Shu-ying, NIU Xing-hui, et al. Research on Influencing Factors of DP600 High Strength Steel U-Bending Springback Based on Dynaform[J]. Die & Mould Manufacture, 2020, 20(4): 32-35.

[21] 郑淇文, 朱春东, 郭宇航, 等. Strenx960先进高强钢折弯回弹控制[J]. 锻压技术, 2020, 45(11): 25-29, 35.

ZHENG Qi-wen, ZHU Chun-dong, GUO Yu-hang, et al. Bending Springback Control of Advanced High-Stre­ngth Steel Strenx960[J]. Forging & Stamping Technology, 2020, 45(11): 25-29, 35.

[22] 钟文, 项辉宇, 冷崇杰, 等. 成形工艺参数对U形件回弹影响的仿真分析[J]. 机床与液压, 2019, 47(19): 145-152.

ZHONG Wen, XIANG Hui-yu, LENG Chong-jie, et al. Simulation Analysis of Springback Effect of Forming Process Parameters on U-Shaped Workpiece[J]. Machine Tool ＆ Hydraulics, 2019, 47(19): 145-152.

[23] 吴信涛, 丁方强, 刘国凯, 等. DP800双相高强钢折弯及回弹研究[J]. 精密成形工程, 2016, 8(4): 38-42.

WU Xin-tao, DING Fang-qiang, LIU Guo-kai, et al. Bending and Springback of High-Strength Dual Phase Steel DP800[J]. Journal of Netshape Forming Engineering, 2016, 8(4): 38-42.

[24] 王东涛, 谢延敏, 郭元恒, 等. 基于Kriging模型的高强钢成形回弹工艺优化和模面补偿研究[J]. 锻压技术, 2021, 46(10): 62-69.

WANG Dong-tao, XIE Yan-min, GUO Yuan-heng, et al. Research on Process Optimization and Die Surface Compensation for High-Strength Steel Forming Springback Based on Kriging Model[J]. Forging & Stamping Technology, 2021, 46(10): 62-69.

Influence Factors and Optimization of U-shaped Bending Springback of DP780 High-strength Steel

DING Hua-feng1,2, PAN Jun-jie1, YAN yang2, JIN Xian-zhi1, LI Hong-bing1, HU Ze-qi1, ZHOU Chang-yu1

(1. School of Automotive and Traffic Engineering, Hubei University of Arts and Sciences, Hubei Xiangyang 441053, China; 2. Hubei Third Ring Forge Co., Ltd, Hubei Xiangyang 441700, China)

The work aims to study the influence of different parameters of DP780 high-strength steel on its U-shaped bending springback. A tensile test was carried out on DP780 steel sheet at room temperature, and its stress-strain curve was obtained. The U-shaped bending die model was used to analyze the U-shaped bending springback with ABAQUS finite element simulation software, and the influence laws of friction coefficient, blank holder force, punching speed and clearance between punch and die on the U-shaped bending springback were studied. On this basis, orthogonal experiments were designed to optimize the influencing parameters. The results show that with a small friction coefficient, the springback will fluctuate slightly. Continue to increase the friction coefficient, the springback will show a decreasing trend. The springback first increases and then decreases with the increase of blank holder force. Change of the punching speed does not have a great impact on the springback. With the increase of clearance between punch and die, the springback gradually increases. The influence magnitude of the four par­ameters on springback is obtained through the orthogonal experiment, and the best parameter combination is5531. Side wall angle1and flange angle2obtained by this parameter combination are the closest to 90°, and the springback effect is the best.

DP780 high-strength steel; U-shaped bending springback; finite element simulation; orthogonal experiment

10.3969/j.issn.1674-6457.2022.10.007

U466;TG142

A

1674-6457(2022)10-0049-07

2021‒12‒01

湖北省教育厅科学技术研究计划青年人才项目（Q20202602）

潘俊杰（1995—），男，硕士研究生，主要研究方向为冲压成形。

丁华锋（1986—），男，博士，讲师，主要研究方向为汽车轻量化设计及制造技术。