图解法用于受迫振动实验的定量研究

何学敏，任银娟，毛巍威，李三龙

(南京邮电大学 理学院，江苏 南京 210023)

1 受迫振动实验的基本现象和问题描述

实验室中通常用波尔共振仪来研究受迫振动，由转动定律可写出摆轮作受迫振动的方程[1]：

(1)

上式中左边项为摆轮的转动力矩，右边三项依次为弹簧回复力矩、电磁阻尼力矩和强迫外力矩。J为摆轮转动惯量，θ为摆轮振幅，k为弹簧弹性系数。

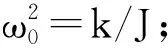
(2)

上式中左边第二项为阻尼项，右边项为受迫项。由《数学物理方法》的知识可得方程(2)的通解为：

θ=θ1e-βtcos(ωft+α)+θ2cos(ωt+φ0)

(3)

上式中右边第一项表示阻尼振动经一段时间衰减消失；第二项表示强迫外力对摆轮做功，传递能量，使其达到稳定的振动状态。

对(3)式而言，需重点关注其稳态解，即受迫振动在稳态时的特征---幅频特性和相频特性。在解析这两大特性时，振幅θ2和相位差φ可表示为：

(4)

(5)

以上即为受迫振动物理模型和数理方程方面的基本描述。

看似复杂的方程和公式，完全可以简化处理。整个实验研究的物理量不出θ、ω0(T0)、β、ω(T)、φ等五个，只需系统测出实验数据，厘清它们与周期(或频率)间的关系，找出特征参数隐含的物理信息，即可对受迫振动实验有较好的理解与掌握。而在此研究过程中，数据处理至关重要。图解法对于大量实验数据的分析非常实用，科学严谨的图像能真实反映和推测出物理量之间的数学关系和变化规律[2]，能拟合得到一些关键物理参数的精确解[3]，能验证和推理出定理、定律背后的物理内涵[4]。

1、家庭方面。在小学生的成长过程中，家长占据着非常重要的地位，需要他们发挥良好模范作用，才能更好的引导小学生养成良好行为习惯。但是，部分家长的教育观念还保持以前传统的方式，经常对着孩子大吼、严厉批评，甚至打骂小学生，致使小学生出现反叛心理。与此同时，部分家长非常宠溺自己的孩子，不让小学生接触各种新鲜的事物，也不让他们自己解决任何问题，从而降低小学生的心理承受能力，甚至影响小学生各方面能力提升。

基于此，本文对自由振动、阻尼振动和受迫振动进行系统研究，利用科研软件规范作图，充分挖掘数据图像的物理意义，得到共振状态下的关键信息，以期对教研人员定性、半定量地研究受迫振动实验起到一定的借鉴作用。

2 自由振动时振幅与周期的关系

理想情况下的自由振动指的是振幅不变且无阻尼(β=0)。但实验上并非如此，用波尔共振仪研究自由振动时，振幅随着时间发生了改变。在自由振动实验中，摆轮是在转动力矩及蜗卷弹簧所产生的回复力矩共同作用下进行的振动。其中，回复力矩用-kθ表示，k是蜗卷弹簧的弹性系数，理论上是一个常数，与扭转的角度无关。但实际上，由于制造工艺及材料性能的影响，弹簧k值会随着角度的改变而发生微小的变化，从而造成在不同振幅时摆轮固有频率ω0(或固有周期T0)也有变化。这种变化不能忽略，如果简单地取所有ω0的平均值来进行计算，将会造成后续受迫振动实验中在共振点附近相位差的理论值与实验值偏差巨大。

显然，在研究阻尼振动和受迫振动的运动特征之前，非常有必要对自由振动下摆轮振幅θ与固有周期T0的关系作清晰的描述。基于此，实验中系统测量了自由振动下的这两组数据，如表1中所示。

表1 自由振动时摆轮振幅θ与振动周期T0的实验数据

由表1可见，自由振动下的摆轮振幅θ从一开始的156°逐渐衰减到结束时的52°，而对应的振动周期T0从1.574s递增到1.590s。在后文研究受迫振动的幅频特性时，将会发现共振处的摆轮振幅为144°，查表1中与此振幅对应的自由振动周期是1.576s。可简单计算出自由振动时固有振动周期T0的最大误差为

(6)

可见，尽管自由振动的固有周期在理论上不变，但实验上却发生了最大0.9%的波动。为了后续研究受迫振动更加严谨，也考虑到同一台实验仪器所测数据的可比性，再将表1数据画成直观的图像形式，如图1所示。

图1 自由振动摆轮振幅θ与振动周期T0之间的关系

图1中的黑色实心方块(■)表示实验测量的数据，而红色实线(-)是基于实验数据线性拟合出的结果。显然，理论拟合的结果较好地契合了实验变化规律，可得自由振动下摆轮振幅与周期的关系式：

θ=10429-6525T0

(7)

有了θ与T0的关系式，在用同一台波尔共振仪研究阻尼振动、受迫振动的运动特征时，凡是要求提供T0值的，均可通过(7)式精确计算出来。这种处理方法将在后文分析受迫振动的幅频特性时得到很好的体现，将有助于共振特征参数的精确求解。

3 阻尼振动中阻尼系数β的确定

阻尼振动是振幅随时间减小的振动，它不受强迫外力矩作用，即mcosωt=0。研究阻尼振动最主要的是得到阻尼系数，并知道怎样选择合适的阻尼档位，以利于后面的共振参数分析。

在阻尼振动中，电磁阻尼力矩包含一个重要的因子，即阻尼系数β，它是通过调节阻尼线圈内直流电流的大小来改变β值。为了后续实验在共振时的振幅大些，便于幅频特性的研究，本实验选用最小的阻尼1档来进行数据测量，得到摆轮作阻尼振动时的振幅数值θ1、θ2、……、θ10，如表2所列。

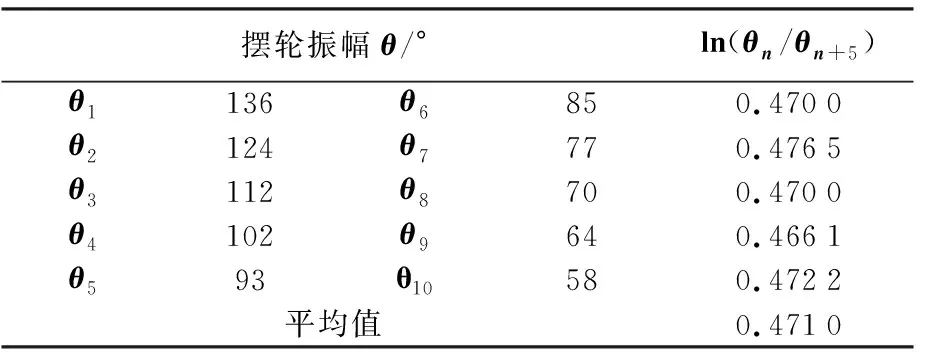
表2 阻尼振动时摆轮振幅θ的测量数据(10T=15.849 s)

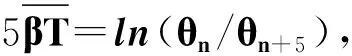
(8)

对于0.059 4s-1这样一个阻尼系数，该值是否理想呢？在后续研究中会发现，该阻尼能使受迫振动的振幅在共振区附近显著下降，在远离共振区阻尼对振幅则影响不大；幅频特性的研究将证明阻尼1档的选择非常合适。

4 受迫振动幅频特性和相频特性的研究

在受迫振动实验中，系统所受的力矩有转动力矩、回复力矩、电磁阻尼力矩和强迫外力矩。其中，强迫外力矩对应于仪器上的“强迫力周期”旋钮，它是通过调节强迫力矩周期电位器来改变电机的转速，即改变强迫外力矩的频率ω，从而改变电机转动周期T。受迫振动实验需待振幅稳定后记录强迫力(即电机)的周期T和摆轮振幅θ，同时用频闪现象测量摆轮与强迫力的相位差φ。在该实验中依次改变强迫力周期，即不断调节电机转速(对应于旋钮刻度值，单位记为a.u.)，测出十几个点，所得数据如表3所示。

研究受迫振动，最重要的就是澄清θ、φ与ω/ω0之间的关系，即幅频、相频特性。基于关系式(4)和(5)，以表3中ω/ω0的数据为横坐标，分别以θ和φ的数据为纵坐标，利用Origin科学作图，可得受迫振动的幅频特性和相频特性曲线。

表3 受迫振动幅频和相频特性的实验数据

在图2所示的幅频特性曲线中，摆轮振幅θ是随着频率比值ω/ω0先增后减，且在ω/ω0=1.00处达到最大值。由红色实线拟合出的结果可以看出，当电机频率ω与系统固有频率ω0一致时，摆轮发生共振，共振振幅θr=144°.由表1可以查出，与摆轮振幅144°对应的固有振动周期T0是1.576s，则可得系统固有频率ω0(=2π/T0)为3.986 8s-1.

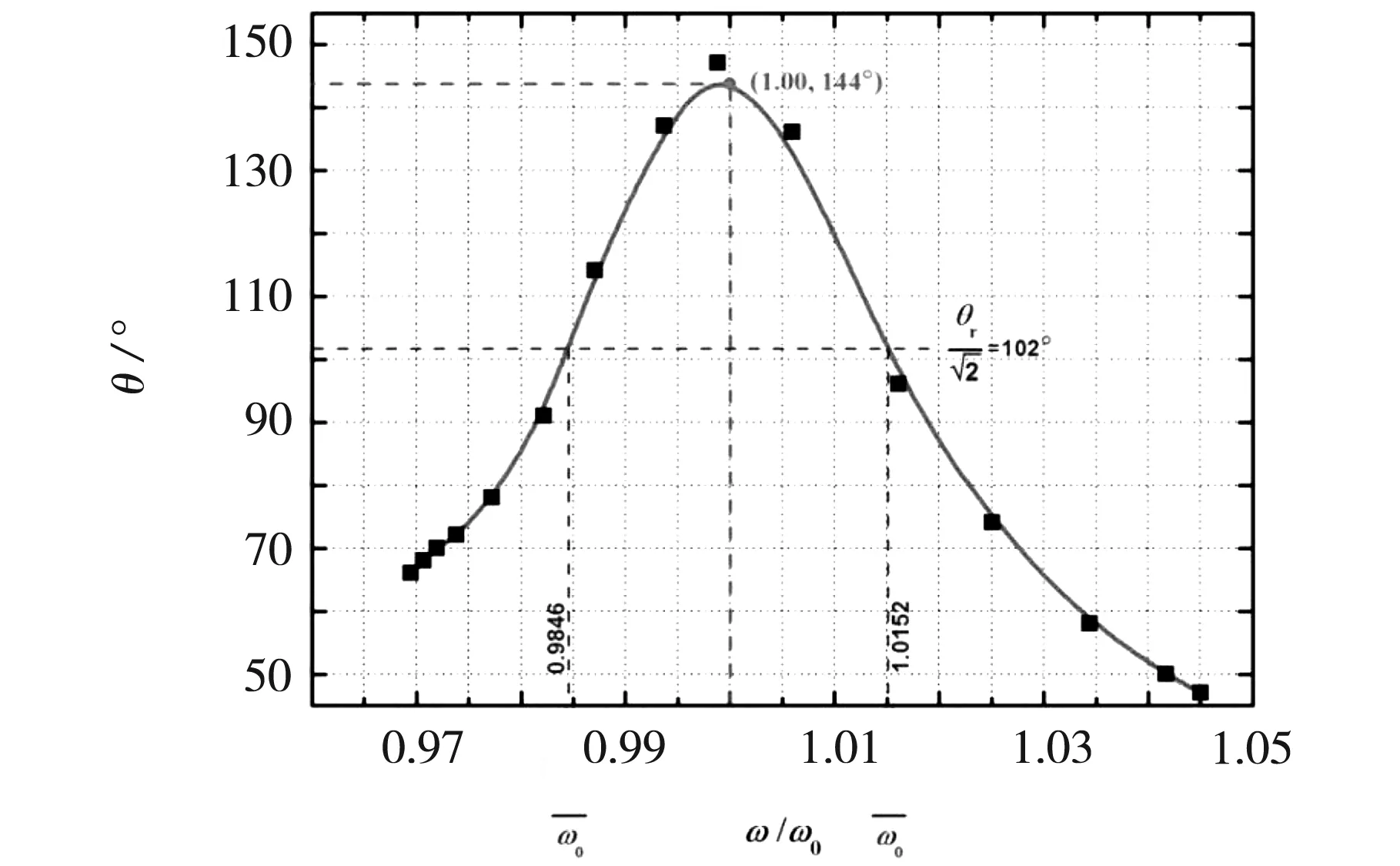
图2 受迫振动时的幅频特性(θ～ω/ω0)曲线.

(9)

(10)

上述两式说明，β趋近于0时，ωr接近于ω0，θr可达无穷大。当然这只是理想上的结果，实际情况就是，阻尼系数β越小，共振时强迫力的圆频率越接近系统固有频率，振幅θr也越大。由前文算得的β=0.059 4s-1和ω0=3.986 8s-1可计算出共振圆频率ωr=3.985 9s-1.可见，此处的ωr和ω0已经非常接近，相对误差只有0.023%，说明前文用阻尼1档来进行阻尼振动的研究使得后面受迫振动时的共振特性达到了最理想的效果。

(11)

(12)

图3 受迫振动时的相频特性(φ～ω/ω0)曲线

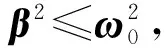
5 结 语

基于波尔共振仪所测的自由振动实验数据，拟合出摆轮振幅与系统固有周期的关系θ=10429-6525T0；结合共振特征参数，发现固有振动周期T0的最大误差为0.9%。基于阻尼振动和幅频特性的实验数据，分别利用逐差法和图解法求出阻尼系数β为0.059 4s-1和0.061 0s-1，二者相对误差只有2.7%。通过Origin软件科学作图得到受迫振动的幅频特性和相频特性曲线；图解法算出的共振圆频率ωr=3.985 9s-1与系统固有频率ω0=3.986 8s-1非常接近，相对误差只有0.023%，说明选用最小的阻尼1档来进行实验是理想的；解析发现，当电机频率与系统固有频率一致时，摆轮发生共振，振幅θr达144°，摆轮与强迫力的相位差φr为π/2，印证了受迫振动时运动方程的稳态解。因此，用图解法对《受迫振动》实验进行定量分析与计算是可行的、成功的，有助于深层次理解数据背后的物理内涵。