基于LabVIEW的虚拟弗兰克赫兹实验仪

李文韬,孙茜茜,余茗舟,陆辰凌,李永涛,王增旭，4*

(1.南京邮电大学 通信与信息工程学院，江苏 南京 210003；2.南京邮电大学 理学院，江苏 南京 210003；3.南京邮电大学 教务处，江苏 南京 210003；4.南京邮电大学 通达学院，江苏 扬州 225127 )

通过对弗兰克赫兹管的理论分析与数学模型的推导与建立，基于LabVIEW语言[1-5]开发了弗兰克赫兹虚拟实验仪器。该仪器可模拟弗兰克赫兹实验的参数设置和数据测量[6-8]过程并模拟示波器显示弗兰克赫兹实验的I-V特性曲线，有助于物理实验的线上教学，并为在线虚拟操作进行了有益的探索。

1 弗兰克赫兹实验原理

弗兰克赫兹实验直接证明了波尔提出的原子能级量子化理论模型，弗兰克赫兹实验的核心主要体现在弗兰克赫兹管上，以充满氩原子蒸汽的弗兰克赫兹管为例做简要介绍。弗兰克赫兹管原理图如图1所示[9]。

通电的灯丝作为弗兰克赫兹管的阴极，从灯丝出来的电子首先会经过第一栅极加速电压，电子在这个区域会获得一个初始速度，进入中间部分。中间部分这个区域充有氩气，在阴极K和第二栅极G2之间加速电压，电子会被进一步加速，同时电子可能会与氩原子发生碰撞。当电子能量小于氩原子最外层电子从基态跃迁到第一激发态所需能量时，电子和氩原子会发生弹性碰撞，两者之间没有能量交换；当电子能量大于氩原子最外层电子从基态跃迁到激发态能量时，电子和氩原子会发生非弹性碰撞，在这个过程中，氩原子吸收电子的部分能量，电子能量降低、速度减小。电子到达第二栅极G2后有一个反向拒斥电压，电子克服反向拒斥电压最后到达阳极，形成电流。

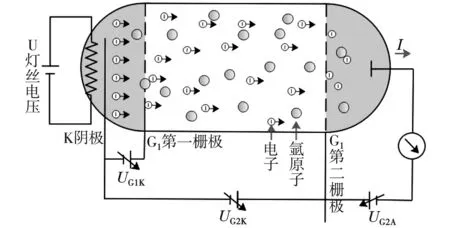
图1 弗兰克-赫兹实验原理图

实验中，通过增加的电压，测得阳极电流与加速电压的关系如图2所示的曲线。

这个实验结果验证了波尔提出的原子里面电子能级量子化的说法，曲线中峰值加速电压的差值就是第一激发电位。

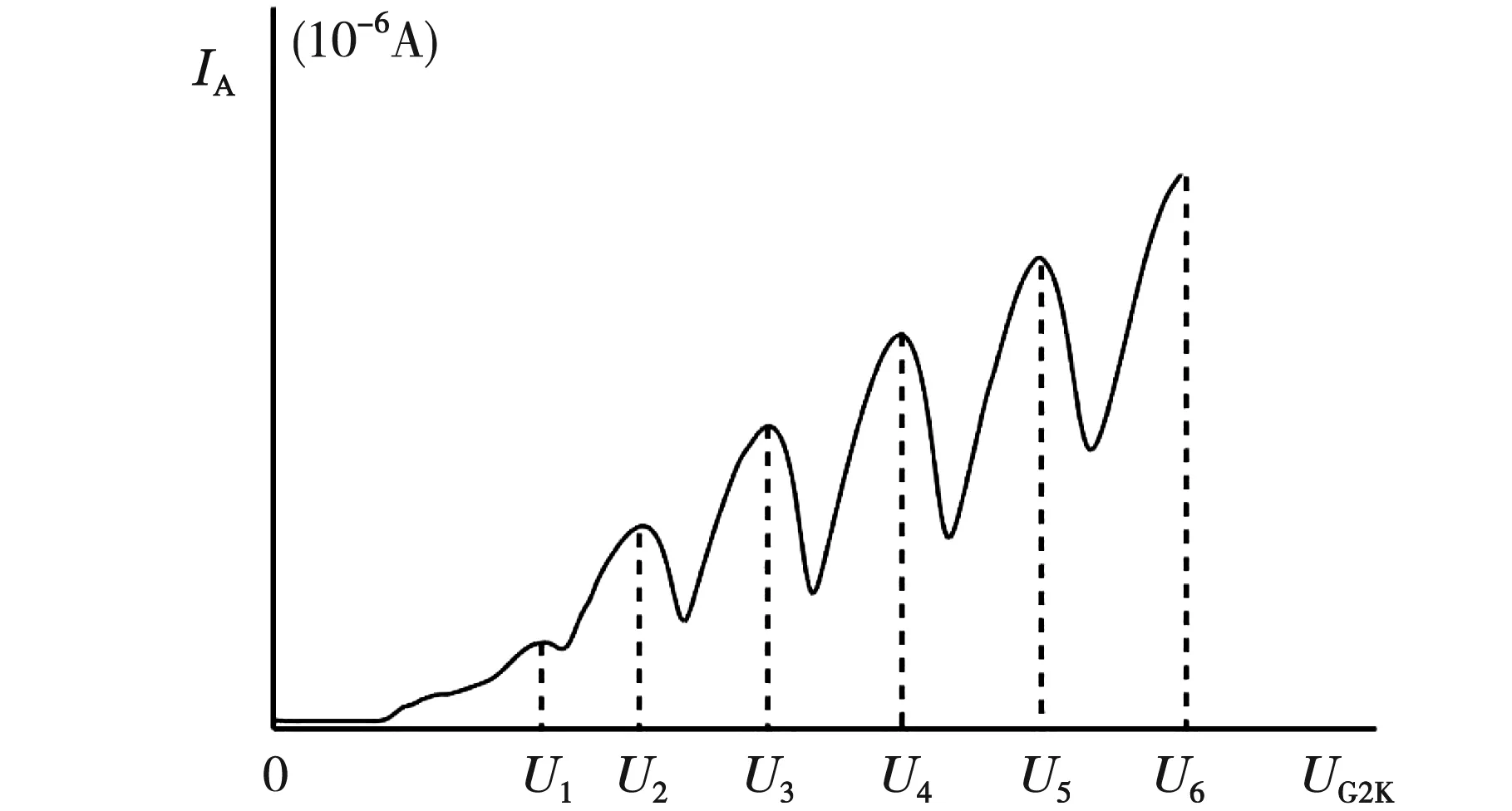
图2 曲线

2 基于LabVIEW的弗兰克赫兹实验仪设计

系统仿真实际实验仪器的功能与效果，前面板提供检流计精度调节、输入参数调节、工作方式选择等，此外还拓展了数据记录与图形绘制功能，可在实验完成后绘制曲线。

2.1 系统前面板设计效果及功能介绍

参照学校当前实验教学中使用的弗兰克赫兹实验仪如图3所示。

图3 FH-2型弗兰克赫兹实验仪面板图

基于LabVIEW设计了虚拟实验仪器的面板与各项参数。效果如图4所示。

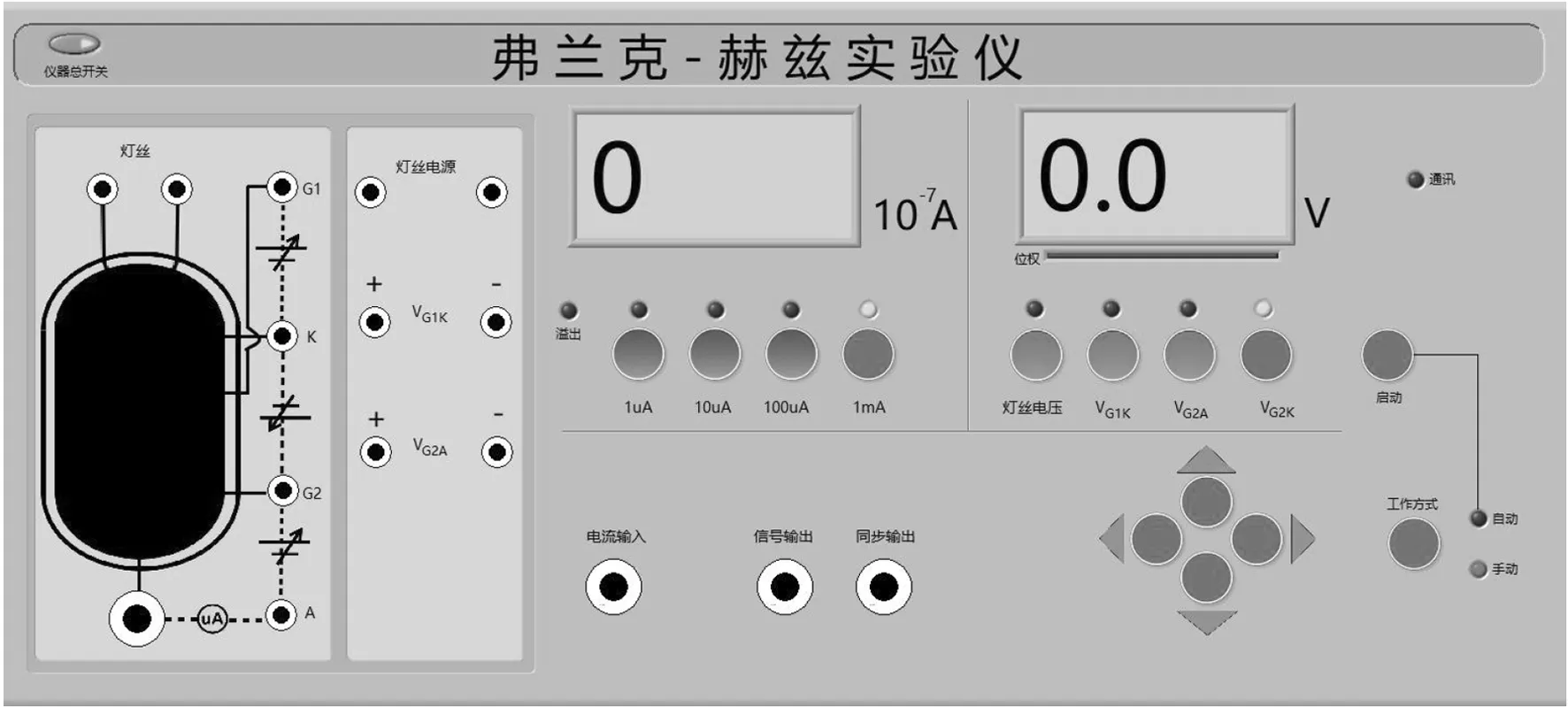
图4 LabVIEW实现的弗兰克赫兹实验仪前面板

弗兰克赫兹实验仪由前面板和作图部分组成。前面板左侧提供电路连线、外接其他仪器等功能，可配合其他虚拟仪器使用，如基于LabVIEW设计的示波器等[2]；中间为电流显示部分，用来体现到达阳极的电流。仪表下方有1 uA、10 uA、100 uA、1 mA四个档位可供选择；右侧为电压显示，在仪表下方有灯丝电压、UG1K、UG2A、UG2K四个按钮，选定对应按钮，可通过下方的左右按键更改位权，再通过上下按键调节对应位权上数值的大小。当灯丝电压、UG1K、UG2A的调节为实验所需参数时，将UG2K、的值从0开始调节，逐步增大，便可以在电流显示部分观察到阳极电流变化。

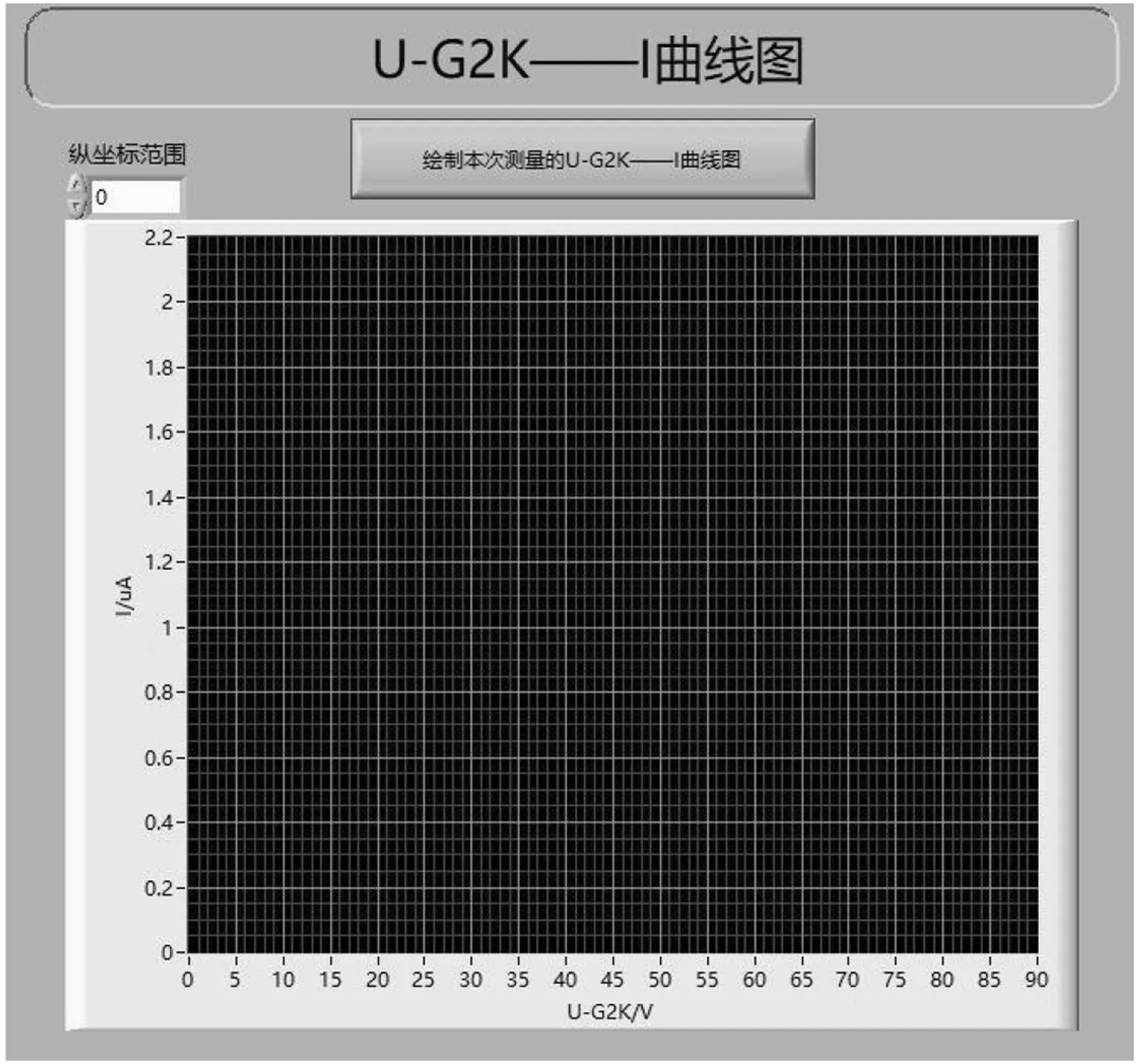
图5 LabVIEW实现的实验仪辅助作图部分

当试验数据大于100组时，点击辅助作图部分的绘图按键，即可基于刚才测量记录的数据绘制出IA～UG2K曲线。该部分还可以根据需要调节坐标轴范围，以便更好地观察与研究数据特征。

2.2 程序框图与参数设置

2.2.1 基础仪器仪表的程序框图

电流表的设计仅涉及精度调节，根据数据的倍乘可以达到效果；电压表显示采用LabVIEW中的选项卡控件，即灯丝电压、UG1K、UG2A、UG2K四个参数通过按键选取，每个参数对应的数据均有对应的显示控件，然后通过选项卡汇总，调整大小后隐去标签，可实现一个区域显示四种不同参数对应数值的效果；电压表下方的上下左右按键可以改变选取参数的值。针对每一个参数的大小调节采用嵌套式条件判断框来处理，权值的选取采用LabVIEW的事件结构来处理，以左键增大调整位权的程序框图为例，如图6所示。此部分整体的程序框图可以用子VI简化设计，为了便于理解，采用直观表述，程序框图7所示：

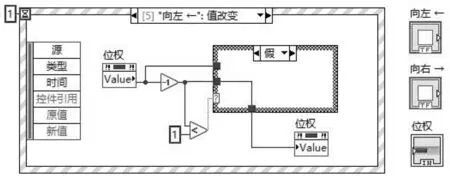
图6 事件结构处理按键选择

图7 基础仪器仪表的程序框图

2.2.2 阴极发射电流的计算

自变量有灯丝电压、UG1K、UG2A、UG2K四个参数，输出的因变量为阳极电流。首先灯丝电压作用于阴极，将钨丝加热。然后钨丝发射电子，从而产生阴极发射电流[10，11]。

金属热电子发射的饱和电流密度公式由Richardson于1912年推导如下，即单位面积所发射的电流与阴极温度遵从：

其中：J为(零场)饱和电流密度(A/cm2)；a为电子发射常数的理论值120.4 (A/cm2)；T为金属工作温度(K)；ω0为金属逸出功(eV)； k为玻尔兹曼常数1.380 649×10exp(23)(J/K)。

通过电流、实验中灯丝电压的表面积与体积参数可计算得到射入弗兰克赫兹管内的电子数[12]。这为下文统计分析管内的电子运动及碰撞情况做数据铺垫。

2.2.3 弗兰克赫兹管的数学模型与程序框图

采取分段式的分析方法描绘弗兰克赫兹管内电子的运动及碰撞情况，由于电子碰撞过程发生第一栅极与第二栅极之间，因此以该部分的分析为例，说明如下：

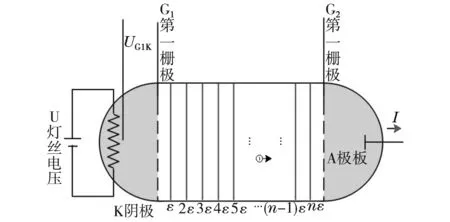
图8 弗兰克赫兹管模型假设

根据充入一定气压的氩气的弗兰克赫兹管的电子的平均自由程[13]，将整个假设长度为30mm的弗兰克赫兹管均分成10 000个单位，记为100ε。整个数学模型过程类似蒙特卡洛模拟，对每个射入的电子情况进行概率上的分析。

电子具有初始动能E=eUG1K。当有1个电子射入后，电子每次前进单位1ε速度与能量也会相应发生变化E=e(UG1K+εU0)。其中，U0=UG2K-UG1K。由于氩原子在管内分布均匀，故在每一个单位内，都会有概率P发生碰撞导致损耗能量。在一个电子走完这10 000个单位后，计算最后的能量，判断是否大于极板电流产生的阈值eUG2A，若大于阈值，则该电子计入数量的统计。然后下一个电子再重复该过程。最后达到预设的电子数量后，统计到达阳极板的电子数，进而进行电流换算。将此过程用LabVIEW程序描述如图9：

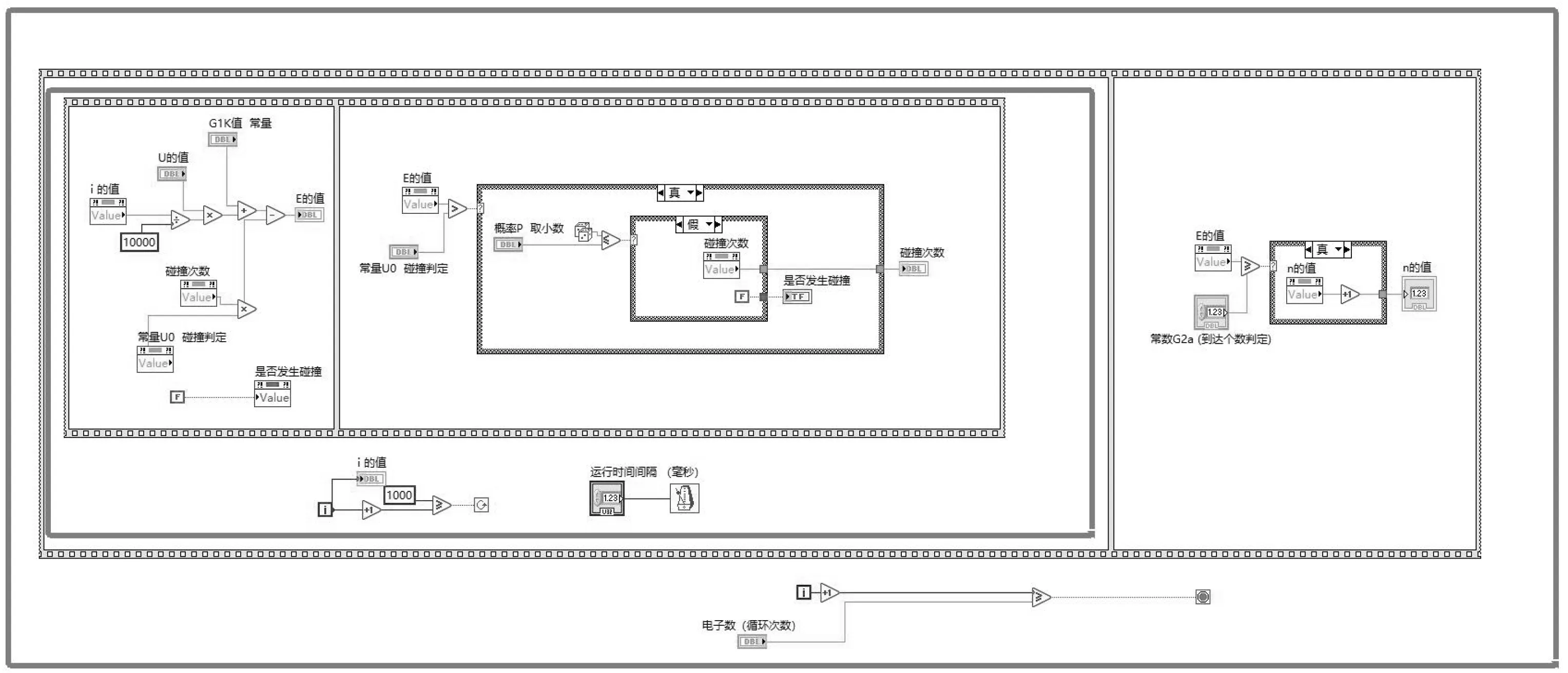
图9 弗兰克赫兹管模块程序框图

程序通过两层while循环嵌套，外部循环控制发射的电子数目，如循环n次，即模拟了n粒电子的运动情况。内部循环控制弗兰克赫兹管的长度ε，每次递增1表示电子前进单位1ε。循环中采用平铺式顺序结构，用来完成电子能量的增加与衰减、电子能否达到极板的阈值判断。

从理论上分析，此方法最契合实际模型，并且具有高仿真、高还原的优点，但是也存在缺点。下图10为10 000个电子在灯丝电压、UG1K、UG2A分别为2.3V、1.5V、9.0V时的实验结果：

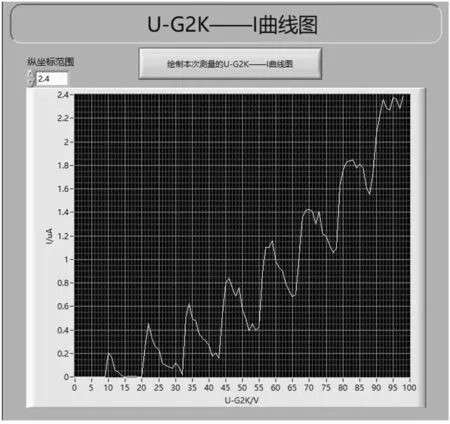
图10 实验数据绘制结果

图10中曲线在大致走向上已经接近实际曲线，但是曲线不够光滑，与实测曲线相比前几个峰值过于尖锐。因为在蒙特卡洛算法中模型过于简化，未考虑原子碰撞过程中散射的方向、实际第一激发态是多个能级的平均效应等因素，这些问题我们另文进行了研究和计算。

当管内模型分段数ε越大，电子数n越多时，通过调节碰撞概率P的值，总能得到接近实际的实验结果。但随着电子数目的增多，LabVIEW程序运行时间也会有所增加，为了达到更高的精度，可以通过调用Matlab程度实现运算[14]，快速返回实验结果，操作步骤如下：

(1)用Matlab语言编写程序，并通过Matlab的coder功能将代码封装成DLL文件以便调用。

(2)在LabVIEW中调用“库函数节点”，在属性中添加上一步的DLL路径。

(3)参数输入设置为UG2K的大小，参数返回存储在新的数组中。

(4)将数组与UG2K的值对应输出，即可实现整个过程。

图10的结果采用的蒙特卡洛算法计算量较大，当电子数取到10 000时，整个计算耗时达30min，这显然不适用于以教学为目的的初衷，因此提供了另一种方法来解决以上问题。

2.2.4 另一种实现仿真的方法与程序框图

基于实验中灯丝电压、第一栅极加速电压和反向拒斥电压是对实验结果的影响[15-17]。选取了8组不同的上述三个实验参量的典型实验结果录入程序的数据库，在进行虚拟仿真时，根据操作者选取的实验参数，调用数据库中已有的数据。

若操作者输入的实验参数在数据库中没有对应数据，将选取在输入参数周边的2组数据进行加权平均，然后输出。以其中一组实验数据为例，程序框图设计思路如图11所示。

该方法不需要程序的调用与实时的蒙特卡洛模拟，却能够得到最真实准确的实验数据，如图13所示。通过数据库的不断完善，可以简便准确的得出输出结果，达到虚拟仿真的效果与目的。

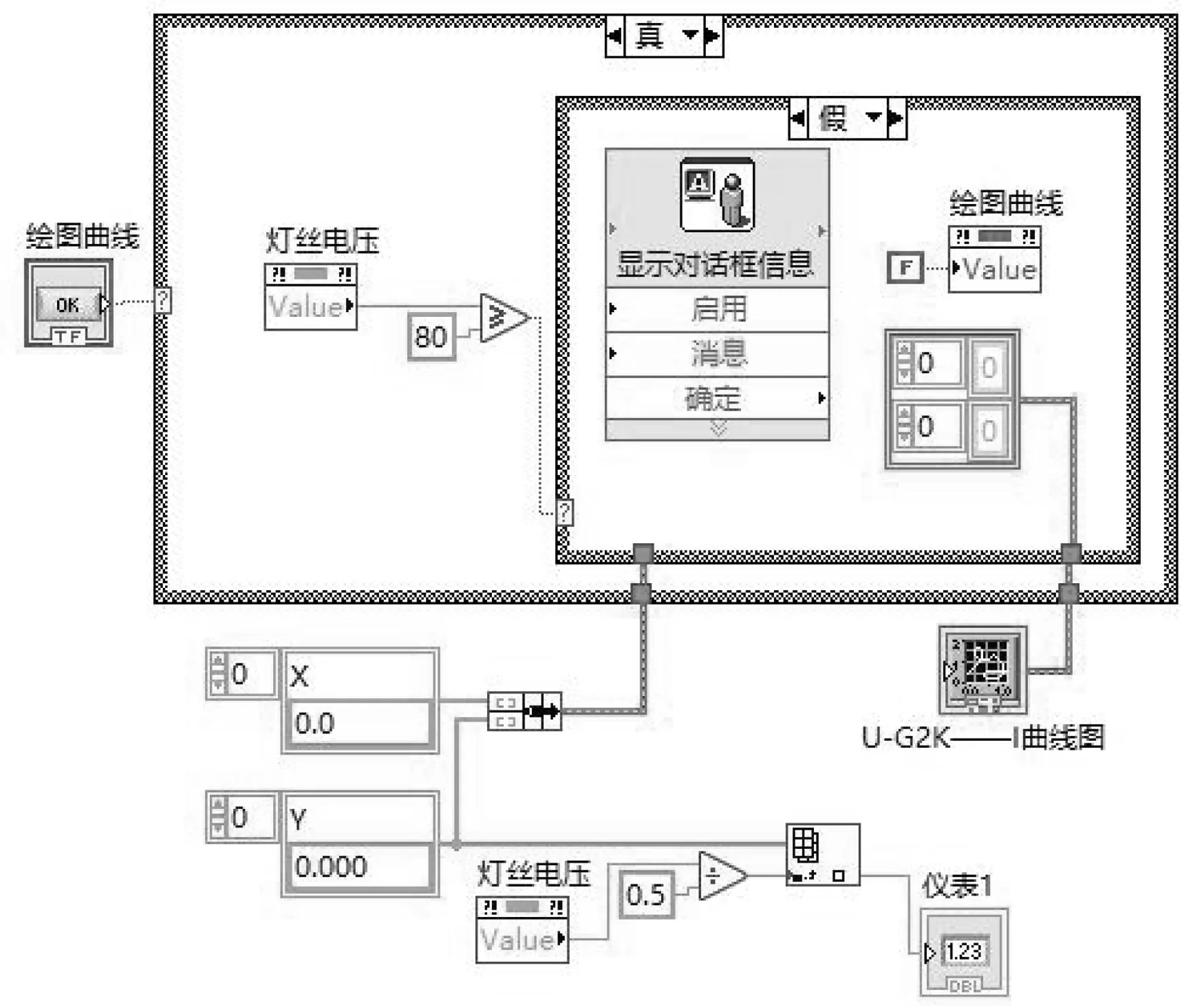
图11 基于已有数据绘制图像

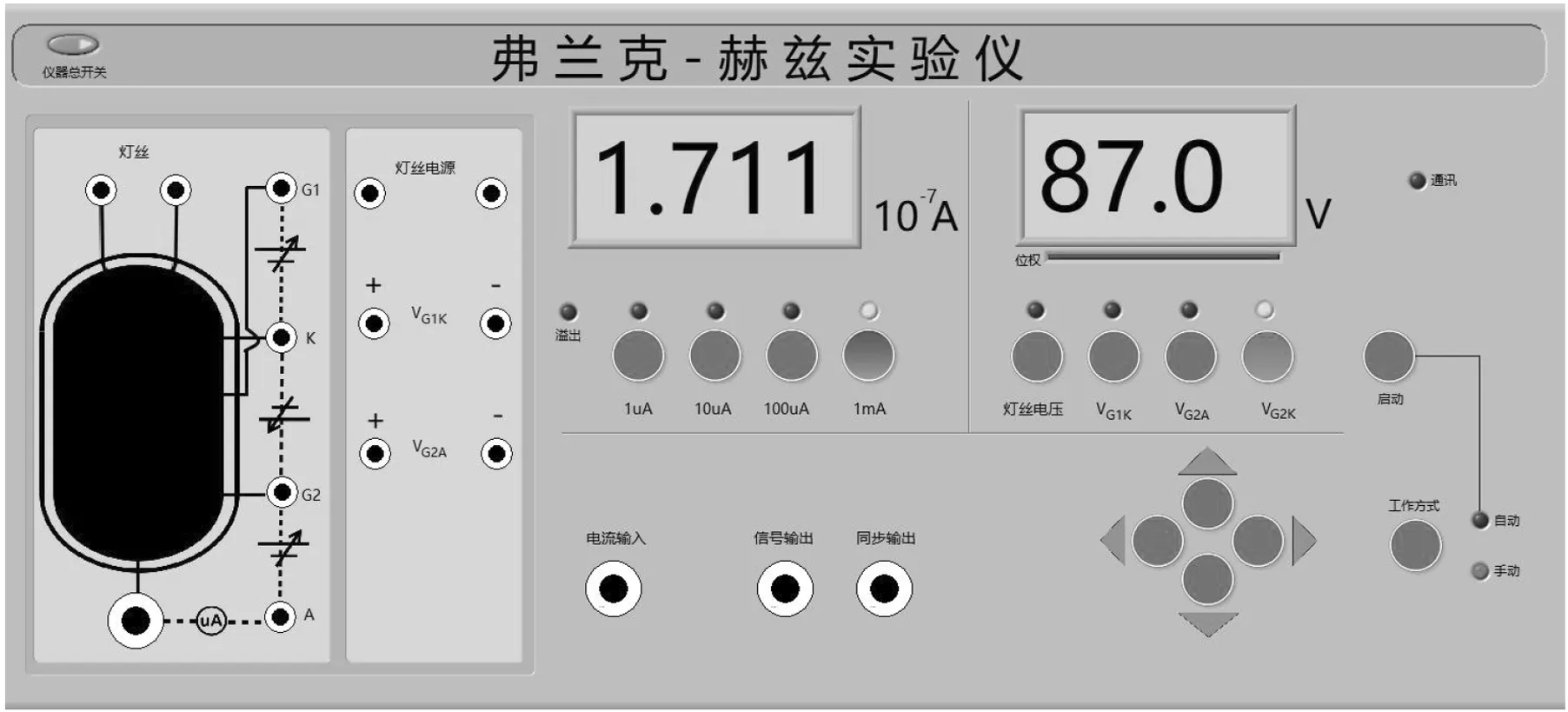
图12 虚拟仪器操作效果

图13 虚拟仪器实验数据绘制结果

3 程序操作及实验结果

程序启动时，电流表电压表示数均归零；选择工作方式为“手动”；

根据实验所需设置灯丝电压、UG1K、UG2A的数值，如本次实验设置的数值分别为：2.3V、1.5V、9.0V；

电流档位调至10-7A；选择UG2K，按向上的增加按钮(每次增加0.5V)，记录电流值，直至观察到电流的六个峰值；

点击程序右侧的绘图按钮，可得到I-UG2K曲线。

4 结 语

通过了蒙特卡洛方法数值模拟弗兰克赫兹实验，并以基于LabVIEW的虚拟仪器呈现，由于计算量巨大，实时的虚拟仿真难以实现，因此通过存储调用典型数据的方式实现了虚拟仿真弗兰克赫兹实验的过程。另外基于LabVIEW的弗兰克赫兹实验仪还提供了数据记录与图形绘制的功能，增加了实际操作的便携性。这为实现物理实验的线上教学提供了新途径。