带耦合电感的五电平混合逆变器

曲冰洁，陈芳，刘佳，李研博

(鄂尔多斯职业学院机动工程系,内蒙古 鄂尔多斯 017004)

近年来,多电平逆变器由于其低谐波失真、低dv/dt和良好的动态性能而成为研究的焦点[1]。为此,诸多学者提出多种拓扑结构,如中性点钳位(Neutral Point Clamped,NPC)[2]、飞跨电容(Flying Capacitor,FC)[3]、级联H 桥(Cascade H-Bridge,CHB)[4]、模块化多电平变换器(Modular Multilevel Converter,MMC)[5]和混合多电平变换器(Hybrid Multilevel Converter,HMC)[6]。为了产生阶梯形输出电压,这些逆变器大都采用电容型电压源、半导体器件和双向传导正向阻断开关[7]。

文献[8]提出一种基于开关电容的7 电平逆变器,采用单直流输入源,并在一定程度上提升了电压增益,但该拓扑结构的升压能力有限。文献[9]提出的多电平逆变器仅需2 个电容便可实现4 倍的电压增益,并输出较多的电平数。文献[10]提出的开关电容多电平逆变器使用扩展方式增加输出电平数。但是该类拓扑需要H 桥来改变输出电压极性,逆变器中开关管承受的最大电压应力会随着输出电压增益的增大而增大,使得实际应用受限。此外,文献[11]介绍了一种拓扑,其在两电平支路或三电平NPC 型支路的上下开关之间使用耦合电感衔接,如图1 所示。该结构提高了有效的PWM 频率、减少了受控开关的数量并且消除了死区时间,从而改善输出电压质量。但是过多的开关器件,导致控制策略过于复杂,很难量产。

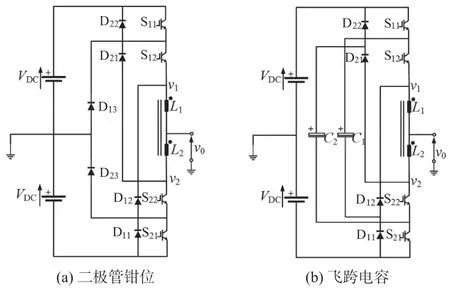
图1 文献[11]中耦合电感五电平逆变器

在上述研究的基础上。本文将介绍带有耦合电感的混合五电平逆变器。该逆变器拓扑具备以下特点:(1)无需H 桥结构就可使输出电压极性改变,实现多电平输出；(2)开关器件承受的最大电压应力较低,具有在高功率场合应用的潜力；(3)该拓扑结构易于扩展,可轻易实现更多电平的输出。最后,实验结果证实了所提出的拓扑结构的可行性。

1 简化模型和运行模态

1.1 混合中性点钳位逆变器

简化混合中性点钳位(Reduced Hybrid Neutral Point Clamped,RHNPC)逆变器的拓扑结构如图2(a)所示。它由三个受控单向导通开关(S11、S12和S21)、三个二极管(D11、D12和D21)、两个磁耦合电感(L1和L2)和两个隔离的直流电压源(VDC1和VDC2)组成。由于耦合电感的电流是单向的,因此只需一个二极管(D11)即可在支路中实现“0”电平。综上所述,D12、S21和D21支持的最大阻断电压为2VDC,其他器件支持的最大阻断电压为VDC。开关状态以及所对应的极点和输出电压如表1 所示。

图2 本文所提的五电平拓扑

表1 RHNPC 逆变器的开关状态

1.2 混合飞跨电容逆变器

本文所提混合逆变器采用三级飞跨电容,即简化混合飞跨电容Reduced Hybrid Flyspan Capacitor,RHFC)逆变器(如图2(b)所示。相较于传统逆变器,所设计的RHFC 逆变器仅需D11和D12来保证飞跨电容的充放电和五电平电压输出,相应的开关状态如表2所示。此外,对于两种所提的拓扑结构,半导体器件的阻断电压如表3 所示。

表2 RHFC 逆变器的开关状态

表3 所提拓扑的最大阻断电压

1.3 耦合电感和电平分析

根据图2 分析可知,逆变器的支路输出电压v1和v2为:

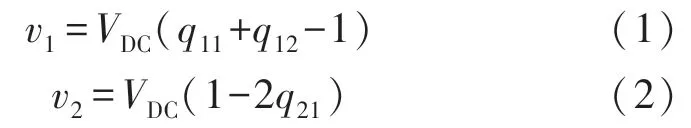
式中:q11、q12和q21是二进制变量,设为0 或1,分别对应于S11、S12和S21的断开或导通状态。从文献[12]中可知,每个支路电压可以被分为共模分量和差模分量的加或减,如式(3)和式(4)所示:

因此,根据图3 所示的等效电路,电压和电流关系可以用共模和差模分量表示为:

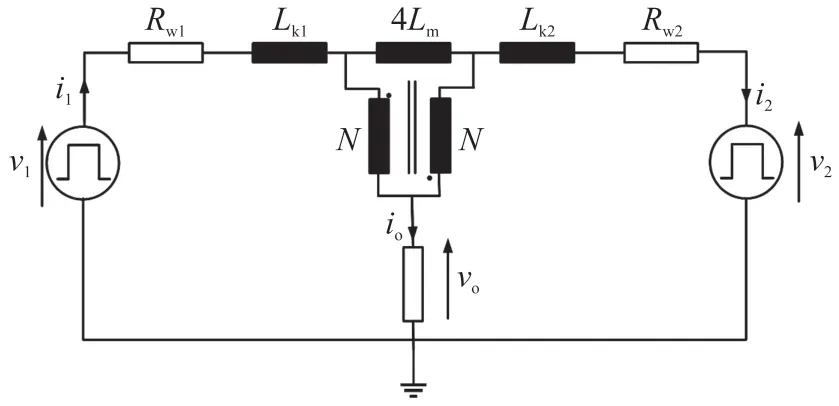
图3 所提拓扑的等效电路

联立式(5)和式(6),解耦模型可由下式计算:

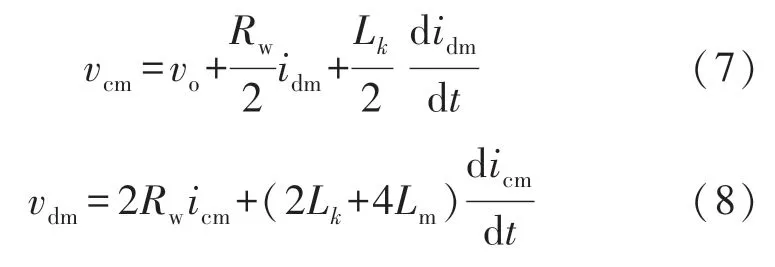
式中:Rw是绕组电阻,Lk＝(1-k)L为漏电感,Lm＝kL是磁化电感,k∈[0,1]是耦合系数。

根据式(7)和式(8)可知,(1)耦合电感的设计影响逆变器性能；(2)耦合电感必须有较高的耦合系数才能获得良好的性能。

2 调制策略和耦合电感的设计

基于文献[13]调制策略的思路,本文将逆变器工作状态划分为两个阶段。详言之,由于电压输出的极性取决于S21的状态,所以图2 中的支路2(v2)应使用低频(电网频率)信号进行调制。然而,v12对于任何开关状态都不为0[13],这将导致磁芯饱和和电感绕组电流不平衡。对此,所提调制策略可保证在切换期间v12的平均值近似为零。

此外,为满足逆变器另一个条件即确保二极管的连续导通[7],差模直流分量(mo)添加至参考电压,如下所示:

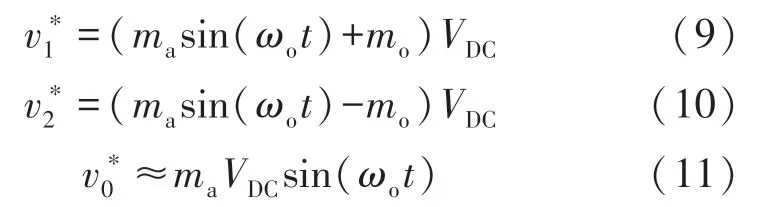
由于式中mo不会影响输出电压,因此共模电压不受此变量影响。

2.1 传统调制方法

对于RHNPC 逆变器,S11和S12选用两个相同电平的移位载波控制。S21由180°相移载波控制,如图4(a)所示。

图4 传统调制

对于RHFC 逆变器,相移载波PWM 可实现电压自平衡,所以它为最合适的选择[14-15]。然而,非对称支路不允许直接使用该调制方式。因此,支路1 使用180°相移载波调制,支路2 使用单个载波调制,在每个开关周期后,其相位在90°和270°之间变化(强制充电和放电时间相同),如图4(b)所示。

2.2 空间矢量调制

表4 为空间矢量调制策略的计算结果,包括向量分配和时间。当-1/3≤ma≤1/3 时,传统调制会在两种拓扑的输出电压处产生过0 的正负电平变化,这会导致THD 性能变差。所提出的空间矢量调制(SVM)通过正确选择矢量来实现低调制指数的两个连续电平之间的切换。

表4 空间矢量调制计算

此外,为确保二极管互补工作,本文所提出的调制策略强制在每个开关周期中切换支路2。因此,向量O2用于正半周期,向量O1用于负半周期。两个逆变器的开关顺序如图5 所示。与传统调制不同,飞跨电容电压不是自然调节,因此需要一个滞环电压控制器来选择合适的矢量P1或N1。

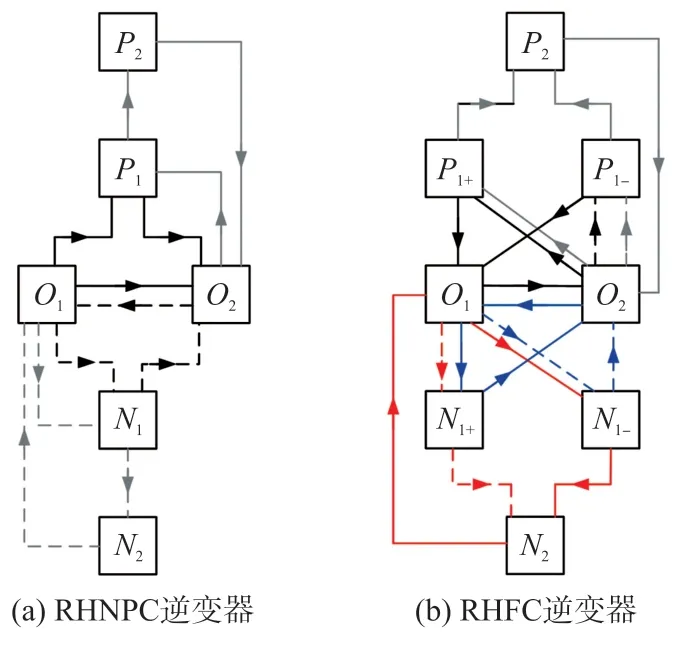
图5 空间矢量调制下的开关切换

2.3 电流纹波分析和耦合电感设计

通过对共模和差模电流纹波的分析,可以确定耦合电感的需求。当vdm等于2VDC时,共模电流的峰-峰值最大为:

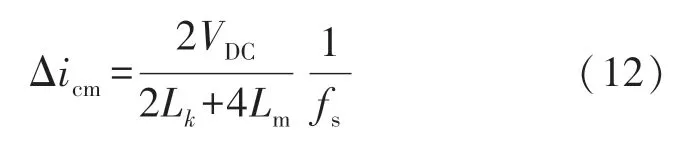
式中:fs是开关频率。

同理,当vcm等于VDC时,差模电流的峰峰值纹波到达最大为:

根据式(13)和式(14)分析,本文选取开关频率为9.6 kHz 以降低差模电流。

此外,根据文献[8]可知,环形磁芯和外部支路中带有绕组的EE 形磁芯适用于此类应用。因为环形磁芯的漏磁通很低,磁芯流量取决于共模电流,而输出电流不会增加大量的磁通。同时,铁芯磁通量可由下式获得:

3 实验结果

为验证所提逆变器的正确性,本文搭建了90 W的实验样机,实验设备采用SKM50GB12T4 IGBT 和SKKD60F17 二极管,控制芯片DSPTMS320F28335。此外,表5 汇总用于仿真和实验结果的参数。

表5 实验参数

图6 在相同的开关频率(9.6 kHz)下,所提出拓扑与现有拓扑总的谐波含量对比。可以看出,所提拓扑具有更佳的谐波抑制性能。图7 为使用传统调制RHNPC 逆变器的仿真结果；图8 为使用传统调制的RHFC 逆变器的仿真结果。可以看出,对于这两种拓扑,电压v1表现出相同的模式,并在降低电压波动的同时完成了飞跨电容的电压调节。

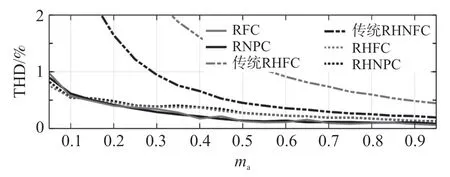
图6 性能比较

图7 传统调制的RHNPC 逆变器仿真结果

图8 传统调制的RHFC 逆变器仿真结果

图9 和图10 分别示了采用SVM 的RHNPC 逆变器和RHFC 逆变器的仿真结果。可以看出,输出电压在[＋VDC/2,0]和[0,-VDC/2]之间切换,其中电压v1在三个电平之间的转换。

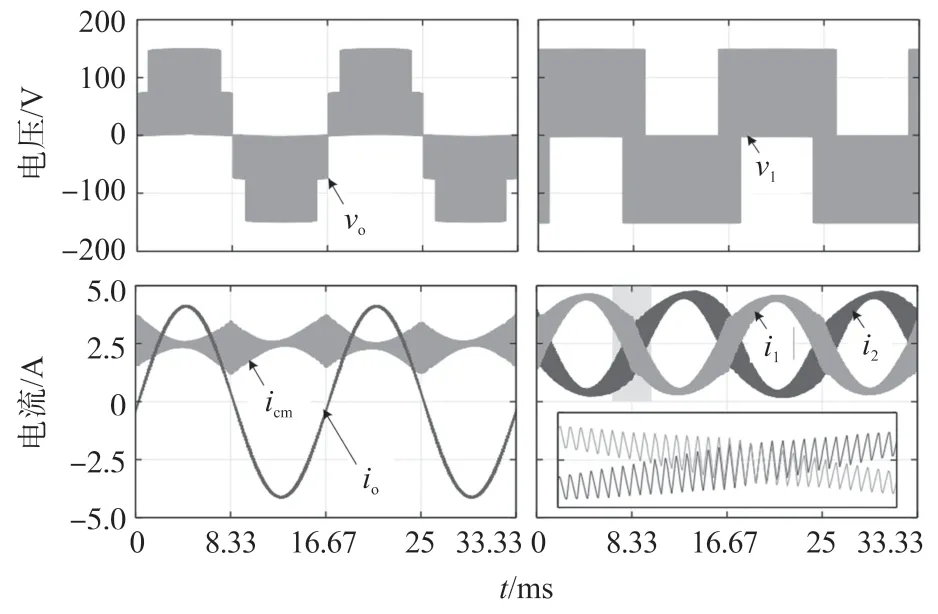
图9 基于SVM 的RHNPC 逆变器仿真结果

图10 基于SVM 的RHFC 逆变器仿真结果

图11 中给出了一个周期的切换模式。可以看到,SVM 的S11和S12同时切换在接近零的区域,这在传统策略不会出现。因此,本文所提拓扑避免了输出电压处-VDC/2、0 和VDC/2 之间的转换,如图12 所示。输出电流不受调制策略的影响。

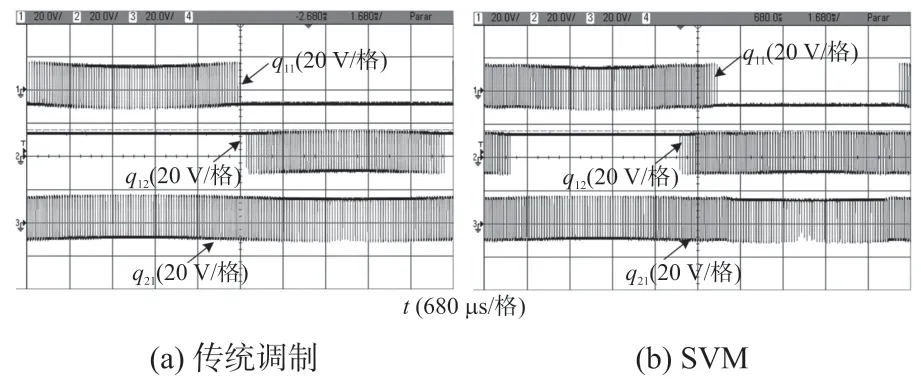
图11 实验的开关模式

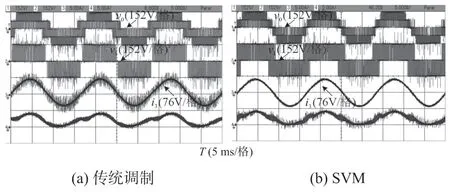
图12 RHNPC 逆变器的主要波形

4 结论

本文介绍了两种使用带有分裂式绕组的耦合电感的五电平混合逆变器,它们提高了高电平数/半导体器件数量的比率。同时本文还提出了两种PWM调制策略,这两种调制策略使逆变器的THD 和损耗更低,然而两电平支路开关器件上的阻断电压也限制了输送到负载的功率。由于这两种拓扑结构有低总损耗、THD 和合适的尺寸,因此它们主要应用在中低功率器件和高速感应电机中。最后,通过仿真和实验结果证明了所提出拓扑的有效性。