典型密码结构的不可能差分区分器研究*

刘 健，毕鑫杰，李艳俊，，金 达

(1.中国电子科技集团公司第十五研究所 信息产业信息安全测评中心，北京 100083；2.北京电子科技学院 密码科学与技术系，北京 100070)

0 引言

1949年Shannon发表了经典论文“Communication Theory of Secrecy System”[1]，该文从抵抗攻击的角度出发，提出了加密算法的“混淆”和“扩散”准则。混淆和扩散成功地实现分组密码明文、密钥和密文之间呈现多种伪随机性质，因而成为现代分组密码设计的重要原则之一。进一步，Shannon还在文章中介绍了代替(Substitution)-置换(Permutation)网络(简称SPN)，其主要是基于代替S盒和P置换两种最基本组件的密码运算，又叫做混合变换(mixing transformations)。不同的混合变换组合成了不同的整体结构，以实现“混淆”和“扩散”的目标。目前分组密码中比较主流的整体结构有Feistel结构、SP结构、广义Feistel结构、MISTY结构等。

随着分组密码设计与分析的发展，一方面算法结构方面的研究越来越细化，比如Feistel-SP组合结构、ARX结构、基于逻辑单元设计的整体结构等[2-4]；同时，以往主要用于分组密码的整体结构越来越广泛地应用于网络空间安全领域的数据快速加密认证体制中，如序列密码设计、Hash函数设计以及认证加密算法设计等，最具代表性的是2018年NIST发起的轻量级认证算法征集活动，第一轮候选算法广泛采用了这些整体结构。另一方面对结构的安全性分析和证明也有了丰富的成果[5-9]。与差分分析、线性分析相比，不可能差分区分器基于截断差分构建，对于差分性能较好的算法攻击效果更好，如对CLEFIA的攻击可以达到13轮[10]，对Camellia的攻击最长可以达到14轮[11]；然而，密码学者们更多地关注具体密码算法的不可能差分安全性，对于一般的结构安全性分析证明较少，以至于新的密码算法设计会出现结构方面的安全隐患，比如2019年全国密码设计竞赛中候选算法TASS1[12]，基于广义Feistel结构设计，并且采用了随机密钥池保证安全性，但是由于未对整体结构进行评估，导致了存在全轮不可能差分区分器[13]。因此，随着信息安全技术及其应用的快速发展，不管是现在还是将来，密码结构安全始终是密码算法安全的首要保障。

本文对Feistel结构、SP结构、广义Feistel结构、MISTY结构四种主要整体结构进行了介绍和研究，重点对广义Feistel结构的TYPE-I型、TYPE-II型和TYPE-III型进行了详细分析，基于这些结构的特点构建了不可能差分区分器，进一步给出了详细证明过程。本文研究希望能够为网络空间安全领域分组密码、序列密码、Hash函数、认证加密等对称密码结构的设计与分析提供参考。

1 Feistel结构

20世纪60年代Horst Feistel设计出基于SP结构的LUCIFER体制，在该体制中没有给出具体S盒，而且加解密不同，需要消耗更多的硬件电路。后来Horst Feistel由“流水线”工作模式想到每次只加密一半的明文数据，进而设计了加解密相似的结构，并以Feistel命名。1967年公开发表的几篇技术报告为Feistel密码结构的安全性研究奠定了基础。加解密相似是Feistel型密码的一个实现优点，但其每轮只对一部分数据进行处理，需要两轮甚至多轮才能改变输入的每一个比特。基于Feistel结构的代表算法有数据加密标准DES、日本分组密码标准Camellia等。

1.1 Feistel结构描述

定义1Feistel结构是一种典型的迭代结构，它能够实现扩散与混乱，构成安全强度高的密码算法。假设圈函数为QK，输入为X0，X1，一轮加密可以表示为：

Feistel结构如图1所示。函数F不一定可逆，可由一些非线性组件和线性组件构成，起到扩散和混淆的效果。

图1 Feistel结构

圈变换QK可以被分解为t◦π，这 里π由π(X0，X1)=(X0⊕FK(X1)，X1)定义。容易验证π是恒等变换，即π是它自身的逆，也称为对合函数；t是交换函数，也是对合的。容易得到圈函数QK逆π◦t。

将Feistel结构迭代r轮，当最后一轮去掉交换时解密过程与加密过程一样，这是因为EK=πr◦t…◦π2◦t◦π1，=π1◦t…◦πr-1◦t◦πr。所以解密时只需将密文作为输入，轮子密钥的次序与加密过程相反。

1.2 不可能差分区分器

性质1假设函数F为随机置换，则Feistel结构存在5轮不可能差分区分器[14]。

如图2所示，对于一个5轮Feistel结构，假设α为非零差分，那么当输入差分为(0，α)时，输出差分为(0，α)的概率为0。证明过程主要利用了F为置换的特点，详细过程见文献[14]。

图2 Feistel的5轮不可能差分区分器

2 SP结构

根据混淆-扩散原则，SP结构设计得非常清晰，由S盒层和P扩散层组合生成。S盒层一般被称为混淆层，主要起混淆作用；P置换一般组成扩散层，主要起扩散作用。在明确S盒和P置换的某些密码指标后，设计者能估计SP结构密码抵抗差分分析和线性分析的能力。SP结构与Feistel结构相比，可以得到更快速的扩散，但是SP密码的加/解密通常不相似，若要相似需采用逆等函数作为组件。SP结构代表算法有国际加密标准AES、韩国标准ARIA、2019竞选胜出算法uBlock[15]等。

2.1 SP结构描述

定义2假设SP结构每轮的圈函数包含三层变换：先是将mn比特明文数据分为n个子块，每块含m比特，即S层为n个S盒并置；然后置换层P为线性变换。S盒是m比特随机置换：，设S盒输入为Xi⊕Ki，输出为Yi；P是线性变换：；最后输出的Zi与轮密钥Ki运算：Zi⊕Ki，1≤i≤n。圈函数用公式描述为：

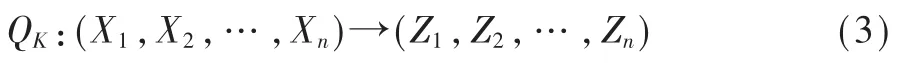
S盒层变换：Yi=S(Xi⊕Ki)，1≤i≤n；P层变换：[Z1，Z2，…，Zn]T=P[Y1，Y2，…，Yn]T。

图3所示为SP结构示意图。

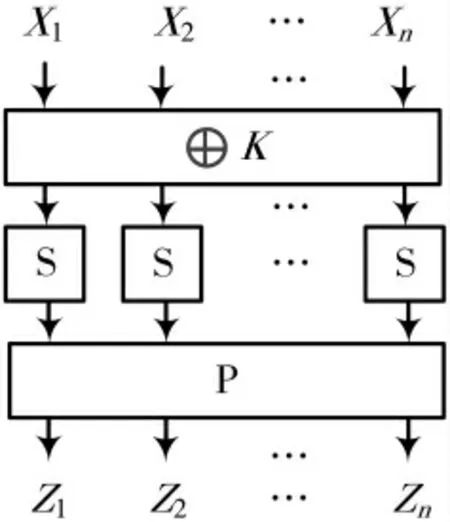
图3 SP结构

SP结构中，由于最后一轮的线性变换没有加强密码性能，同时为了减小加解密变换的差异，因此在设计迭代结构时通常将最后一轮的线性变换省略掉。这种SP结构既可以用来构建分组密码算法的整体结构，例如AES、uBlock；也可以作为Feistel整体结构中圈函数的部件，例如SM4、CLEFIA、Camellia等算法。

2.2 不可能差分区分器

性质2对于SP结构密码算法，若S盒为随机置换，那么无论P取哪一种线性变换，必存在2轮不可能差分区分器[16]。

性质3若扩散层P对应系数矩阵中的元素含0，则基于字节(半字节)设计的SP结构存在3轮不可能差分区分器[16]。

采用二元域上矩阵作为扩散层P，则矩阵中必有零元素出现。根据这个性质容易推出3轮不可能差分区分器，如图4所示。

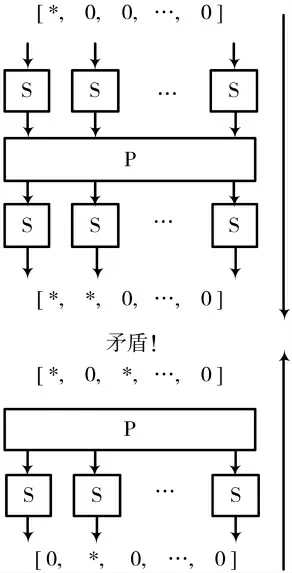
图4 SP结构3轮不可能差分路径

在实际使用的分组密码算法中，扩散层P通常由多级扩散构成，结合S盒差分分布表，通常存在更多轮数的区分器，如AES、ARIA、uBlock都存在4轮不可能差分区分器[16]。

3 广 义Feistel结构

广 义Feistel结 构(Generalized Feistel Structure，GFS)[17]是Feistel结构的推广，特点是对分组再进行小分块处理，使同时处理的分块长度较小。目前出现的主要有TYPE-I、TYPE-II、TYPE-III三种结构。2010年FSE会议上Suzaki等人基于图论的知识对TYPE-II型进行了改进，减小了全扩散的轮数[18]。

3.1 广义Feistel结构描述

基于TYPE-I结构设计的分组密码有CAST[19]、SMS4等；基于TYPE-II结构设计的分组密码有CLEFIA等；基于TYPE-III结构设计的分组密码有MARS[20]、轻量级LEA[21]等；基于改进TYPE-II结构设计的分组密码有轻量级LBlock、TWINE[22]等。下面对TYPE-I、TYPE-II和TYPE-III型结构依次进行介绍和不可能差分区分器证明。

定义3假设输入一组明文分成n个子块，即X0，X1，…，Xn-1，定义一个函数FK(不要求可逆)，则圈函数可以表示成：

由这种方式获得的函数被称为TYPE-I型结构，其结构如图5所示。

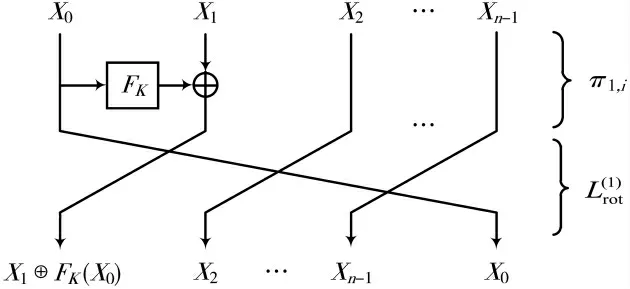
图5 TYPE-I型结构

TYPE-I型结构迭代r轮后，加密变换EK=π1，r◦◦π1，1，解密变换◦…◦π1，r-1◦◦π1，r，不仅要变换轮密钥顺序，还需改变循环移位的方向。

定义4假设输入一组明文分成n个子块，即X0，X1，…，Xn-1，定义一个函数FK(一般情况下是双射)，则TYPE-II圈函数可以表示成：

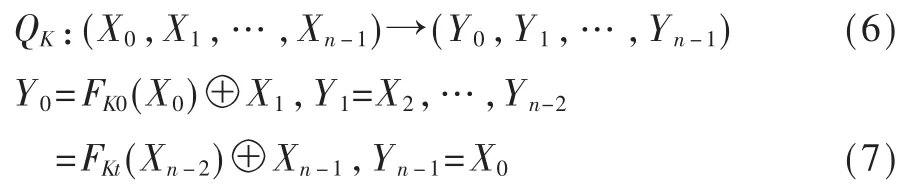
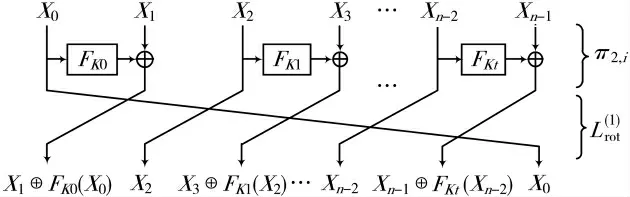
图6 TYPE-II型结构

TYPE-II型结构迭代r轮后，加密变换EK=π2，r◦，解密变换◦…，不仅要变换轮密钥顺序，还需改变循环移位的方向。

定义5假设输入一组明文分成n个子块，即X0，X1，…，Xn-1，定义一个函数FK(一般情况下是双射)，则圈函数可以表示成：

其中t=n-2，称由这种方式获得的函数为TYPE-III结构。

基于TYPE-III设计的分组密码相对较少，MARS和LEA算法基于这种结构设计。

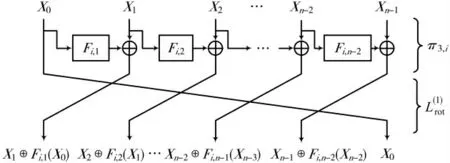
图7 TYPE-III型结构

TYPE-III型结构迭代r轮后，加密变换EK=π3，r◦，解密变换◦…◦，不仅要变换轮密钥顺序，还需改变循环移位的方向。

3.2 不可能差分区分器

性质4设函数F是随机置换，则n轮全扩散的TYPE-I型分组密码必有n2+n-1轮不可能差分区分器。

证明：TYPE-I型分组密码扩散较慢，所以以表的形式给出各轮输入差分模式。如表1所示，对于n分块的TYPE-I型结构输入差分为[0，0，0，…，0，0，a]，经过n轮加密之后为[ΔF(a)，0，0，…，0，0，a]，ΔF(a)为非零值；再经过n-1轮，即在第2n-1轮输入处差分为，，因为⊕a=?，差分值 不 确定，而为非零，所以记作[?，*，*，…，*]；在加密方向继续推导，在第2n+1轮输出处差分模式为[?，*，*，…，⊕a，?]。其中“*”表示非零子块。

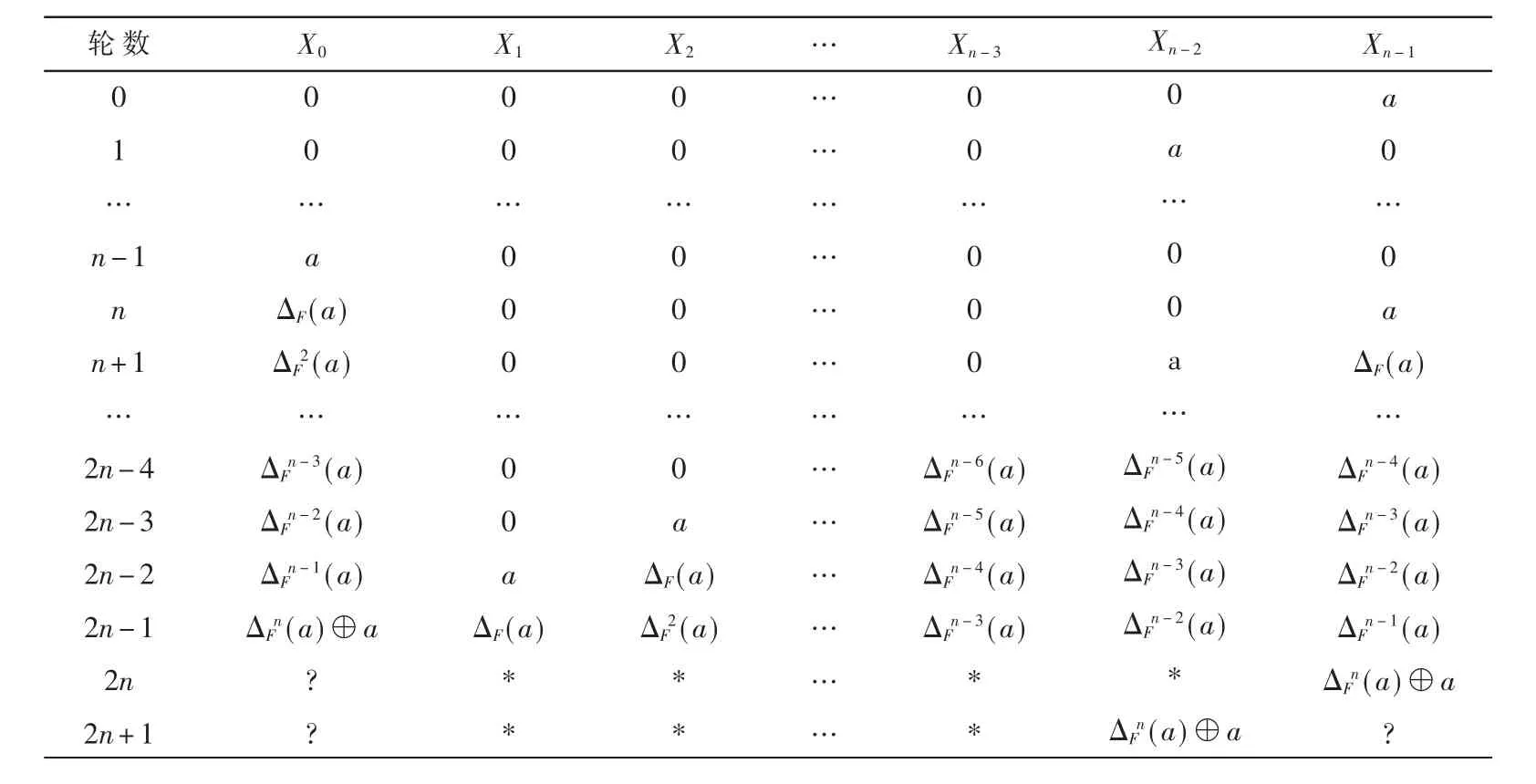
表1 TYPE-I型结构加密方向差分模式

如表2所示，假设若干轮加密后输出差分模式为[a，0，0，…，0，0，0]，解密方向经过1轮输出[0，a，0，…，0，0，0]，容易推导出n2-n-2轮后输出为[?，?，?，…，?，a，?]，共解密n2-n-2轮。与加密方向第2n+1轮输出处差分模式[?，*，*，…，⊕a，?]发生矛盾，所以共有n2-n-2+2n+1=n2+n-1轮不可能差分区分器，如图8所示。

图8 TYPE-I型不可能差分区分器

表2 TYPE-I型结构解密方向差分模式

例如，当分块为3时，容易推导不可能差分区分器轮数为8；当分块为4时，如MARS-256算法，容易验证其区分器轮数大于15。

性质5设函数F是随机置换，则n轮全扩散的TYPE-II型分组密码必有2n+1轮不可能差分区分器。

证明：n轮全扩散的TYPE-II型结构分块为n，下面从加密方向和解密方向进行推导。

在加密方向，假设n个子块X0，X1，…，Xn-1的输入差分模式为[0，0，…，0，a]，即Xn-1处差分非零，其余子块差分全为0，经过n轮变换之后输出差分模式为[*，*，…，*，a]。

在解密方向，假设第2n+1轮输出的n个子块[X0，X1，…，Xn-1]差分模式为[0，0，…，a，0]，即Xn-2处差分非零，其余子块差分全为0，经过n轮解密变换之后得到第n+1轮输出差分模式为[*，*，…，a，*]。

由于第n+1轮输入Xn-2的差分非0，Fk是置换，因此此处出现矛盾，即不可能出现Fk(Xn-2)⊕a=a。图9为2n+1轮不可能差分区分器。

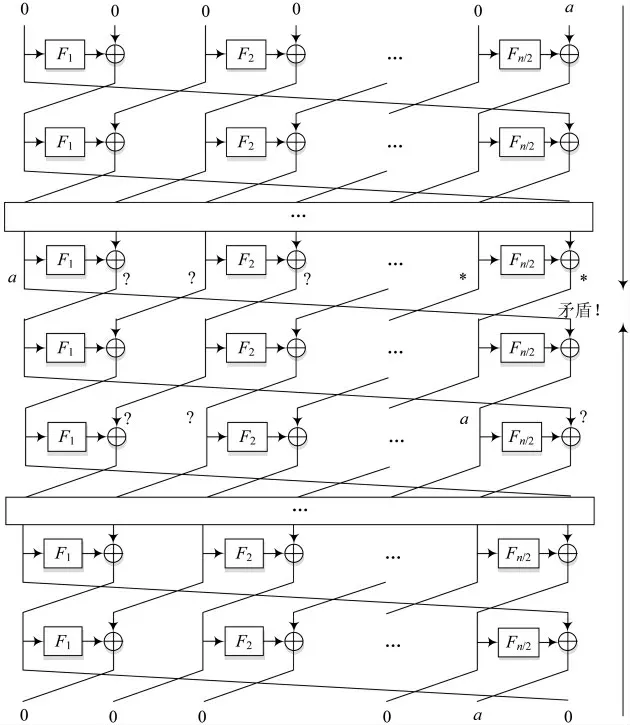
图9 TYPE-II型不可能差分区分器

性质6设函数Fi是由密钥控制的随机置换，则n个子块的TYPE-III型分组密码必有n+2轮不可能差分区分器。

证明：如图10所示，假设输入差分模式为[0，0，…，0，a]，经过2轮加密变换为[0，0，…，a，ΔFn(a)，0]，由于ΔFn(a)为非零，可以记为“*”，n轮加密之后第n+1轮输入为[?，?，…，?，*，a]；假设第n+2轮输出为[0，…，0，a，0，0]，解密1轮并经过循环移块之后得到[*，0，…，0，0，a]，由于Fn为随机置换，因此非零差分“*”输入，输出差分必定非零，即Fn(*)⊕a≠a，此处矛盾。

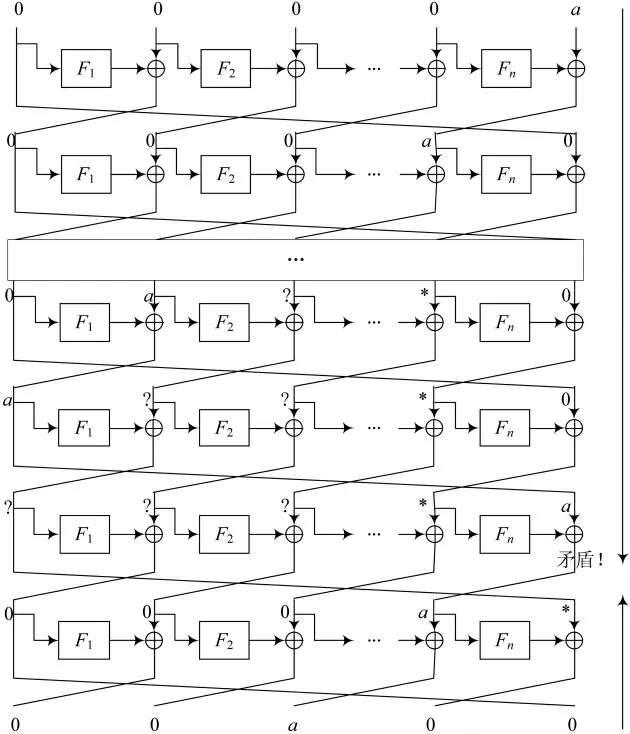
图10 TYPE-III型不可能差分区分器

因此，n个子块的TYPE-III型分组密码必有n+2轮不可能差分区分器。

4 MISTY结构

MISTY结构[23]由日本著名密码学家Mitsuru Matsui等人于1995年提出，基于此结构系列算法被设计出，包含MISTY1、MISTY2和KASUMI，其中KASUMI算法是基于MISTY1算法的改进版本，是第三代移动通信技术中的一种核心加密算法。

4.1 MISTY结构描述

定义6假设输入明文P为X0，X1，密钥为K，输入函数为F，则MISTY圈函数可以表示为：

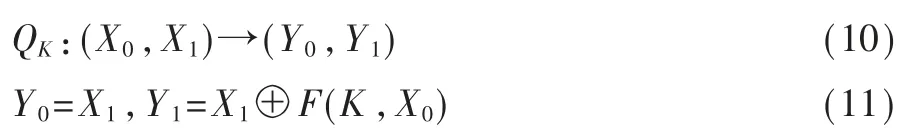
如图11所示，MISTY结构类似于Feistel，函数F只对输入的一半数据加密。

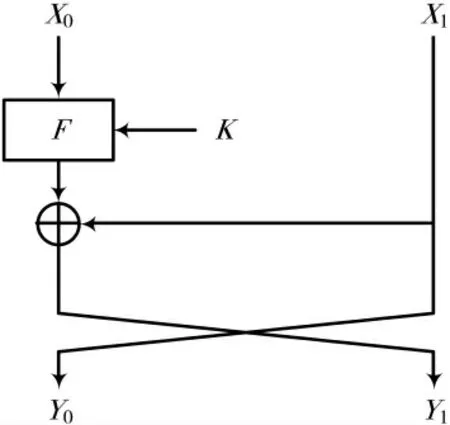
图11 MISTY结构

4.2 不可能差分区分器

性质7当Fi函数(1≤i≤4)为随机置换时，MISTY至少存在4轮不可能差分区分器[23]。

如图12所示，假设输入差分[x0，y0]=[α，0]，经过两轮变换之后在y1处必为非零；再假设4轮加密之后输出差分为[x2，y2]=[β，β]，经过两轮解密之后在y1处必为零。由此构成矛盾，所以[α，0]→[β，β]为4轮不可能差分区分器。

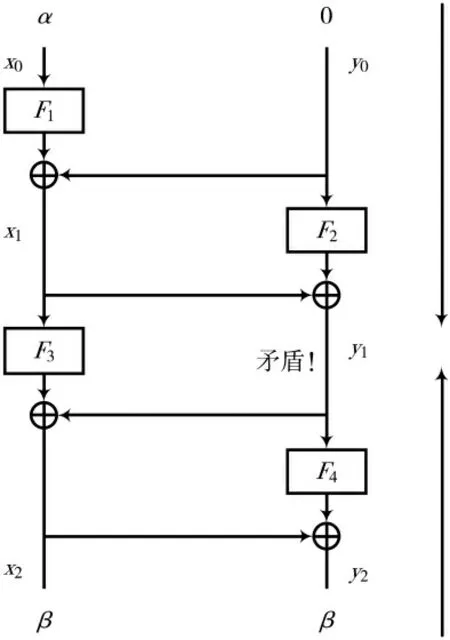
图12 MISTY的4轮不可能差分区分器

5 结论

本文对四种主要密码整体结构进行了不可能差分区分器介绍和研究，重点给出了TYPE-I、TYPE-II和TYPE-III型结构的不可能差分区分器证明过程。虽然这些密码整体结构有一定长度的区分器，但是当设计具体密码算法时，由于无法使圈变换中F函数完全随机，因此基于这类结构设计的对称密码算法往往有更长的不可能差分区分器，如基于SP结构设计的AES、ARIA都存在4轮不可能差分区分器，基于TYPE-II设计的CLEFIA存在9轮不可能差分区分器。因此关于对称密码整体结构在不同计算模型下的细化研究和分析是本文下一步的研究重点。