基于光量子计算的信用评分特征筛选研究报告

文 凯，马 寅，王 鹏，朱德立

(1.北京玻色量子科技有限公司，北京 100016；2.光大科技有限公司，北京 100083)

0 引言

目前，量子计算是未来的计算发展趋势,全球各主要研究机构和公司选用不同的物理方案来制造量子计算机，主流的技术路线包括超导量子计算、光量子计算等。超导量子计算系统对环境要求苛刻，要求在绝对零度附近的超低温下才能工作；光量子计算其原理是使用光量子的叠加态对组合优化问题进行指数级求解加速。基于光量子系统的相干伊辛计算架构(Coherent Ising Machine，CIM)[1]，具有光量子常温下编码操控和其在相干时间、室温工作、全联接等方面的技术优势。目前，国内北京玻色量子科技有限公司等企业，已完成第一台全国产光量子计算原型机的设计制造。

CIM可以充分利用光量子常温下编码操控的技术优势，实现100～100 000量子比特的量子计算的有效应用和算法优越性验证[2]，并且可以广泛地应用于生物制药、交通、人工智能[3-7]等领域。在金融风控领域，特别是在信贷业务场景下，需要利用客户多维度的特征，对客户未来的违约行为做出预测，从而进行风险控制决策。因此好的风控评估模型能为银行风控业务提供从资产负债、信用风险、反欺诈、反洗钱等全方位完整的风险控制方案。在建立风控模型的过程中，随着大数据时代的到来，客户数据维度呈指数型增长，传统的特征筛选方法需要人工经验的参与，对大维度数据的处理显得较为吃力，亟需创新式的解决方案。量子计算作为超强算力的代表，在此领域拥有极大的潜力。

在信用评分的建模场景中[8]，特征选择在整个过程起着至关重要的作用，通过筛选后续入模的特征从而提高模型的准确率和效率，并具有更好的泛化能力。尤其是在特征数较大时，不同特征的选择将决定最后信用评分模型的整体效果。本文将采用传统信用评分的建模逻辑，对于特征筛选这一环节，采用量子计算的方式进行优化，从而对整体模型效果进行提升(并与传统方式的特征选择进行对比)。通过建立相应的二次无约束二值优化(Quadratic Unbounded Binary Optimization，QUBO)[9]模型来实现特征选择，该模型理想情况下选择既独立又有影响力的特征。此次研究主要通过量子计算解决QUBO模型来实现特征选择，相比传统信用评分的特征选择，在不牺牲准确率的前提下，量子计算效率更高而且人工干扰更少，并在特征数很大时，解决了人工筛选难度大的问题。

1 数据及预处理

本文采用的数据是德国信用数据，其中包括20个特征(7个数字特征，13个分类特征)和1个二元分类特征(良好信用或不良信用)。在此基础上，本文采用了两种数据预处理的方式。

方式A：将分类特征进行one-hot编码[10]，使得特征数增加为48个；

方式B：采用传统信用评分业务中的建模逻辑，对原始数据进行WOE分箱处理，不改变原有的特征数。

将处理后的数据作为QUBO模型的输入，用量子计算机求解QUBO模型，输出选择后的特征子集。

经过预处理后，得到一个m行，n列的矩阵U，每一列代表一个特征，每一行表示信用申请人的相应数据值。

历史信用记录表示为m个元素的向量V：

其中原始数据中代表信用credit的数据值(vi)为01变量，0表示接受，1表示拒绝信贷申请。

在建立QUBO模型时，需要计算特征之间的相关性及每个特征对信用V的相关性，而实验A、B也采用了不同的处理方式：

实验A：用斯皮尔曼相关性计算方法

实验B：沿用斯皮尔曼相关性计算特征之间的相关性，用信息变量(Information Value，IV)值替换特征与信用数据之间的相关性。

2 特征选取

特征选取作为一种数据预处理策略，已被证明可以适用在各种数据挖掘和机器学习问题上，且对最终模型效果起到显著的作用。特征选择的目标包括构建更简单、更容易理解的模型，提高数据挖掘性能，以及准备干净、可理解的数据。从方法论上讲，为了强调传统数据现有特征选择算法的异同，一般分为四类[11]：基于相关性[12]、基于信息理论[13]、基于稀疏学习和基于统计的方法[14]。本文主要讨论了两种特征选取策略：基于相关性的传统特征选取；基于量子计算的特征选取。

2.1 传统特征选取

假设从n个特征的原始集合中想要选择具有m个特征的一个子集，用于做出信用决策。首先，通过IV值筛选掉对结果影响不大的冗余特征，在此基础上选择出相关性较高的特征对。

2.2 量子特征选取

从数学上讲，特征选取的目标将是找到与向量V相关，但彼此不相关的矩阵U的列。令ρij表示矩阵U的第i列与第j列的相关性，ρVj表示U的第j列与V的单列的相关性。为了找到“最佳”子集，本文引入了n个二进制变量xj，它们具有如下数学含义：

将这些元素共同组成向量X，形如：

筛选最佳特征子集，求解最小化目标函数对应的X的值，目标函数由两部分组成：第一个部分表示特征对被标记的类的影响为：

第二个组成部分代表了独立性为：

引入参数α(0≤α≤1)以表示独立性(在α=0时最大)和影响性(在α=1时最大)的相对权重并得到如下的目标函数为：

QUBO模型的数学表达式为：

其中xi为待求二进制变量，取值为{0，1}，qij为二次项系数，为已知量，当i=j时，将简 化 为xi。将f(x)写成线性代数的形式：

通过CIM求解向量X*，从而得到筛选后的特征子集为：

固定超参数α的值后筛选的特征结果如下：

(1)超参数α的值为0.977时，特征选择从48个特征中得到的特征数量是24个，使得模型的预测准确率达到极大值。由于其中的分类特征经过one-hot编码之后没有直观的意义，在此不再与传统筛选的特征进行比对，只在后续的准确率计算中进行比对。

(2)超参数α的值为0.97时，特征选择从20个特征中选取12个特征，统手工筛选出13个特征，如表1所示。

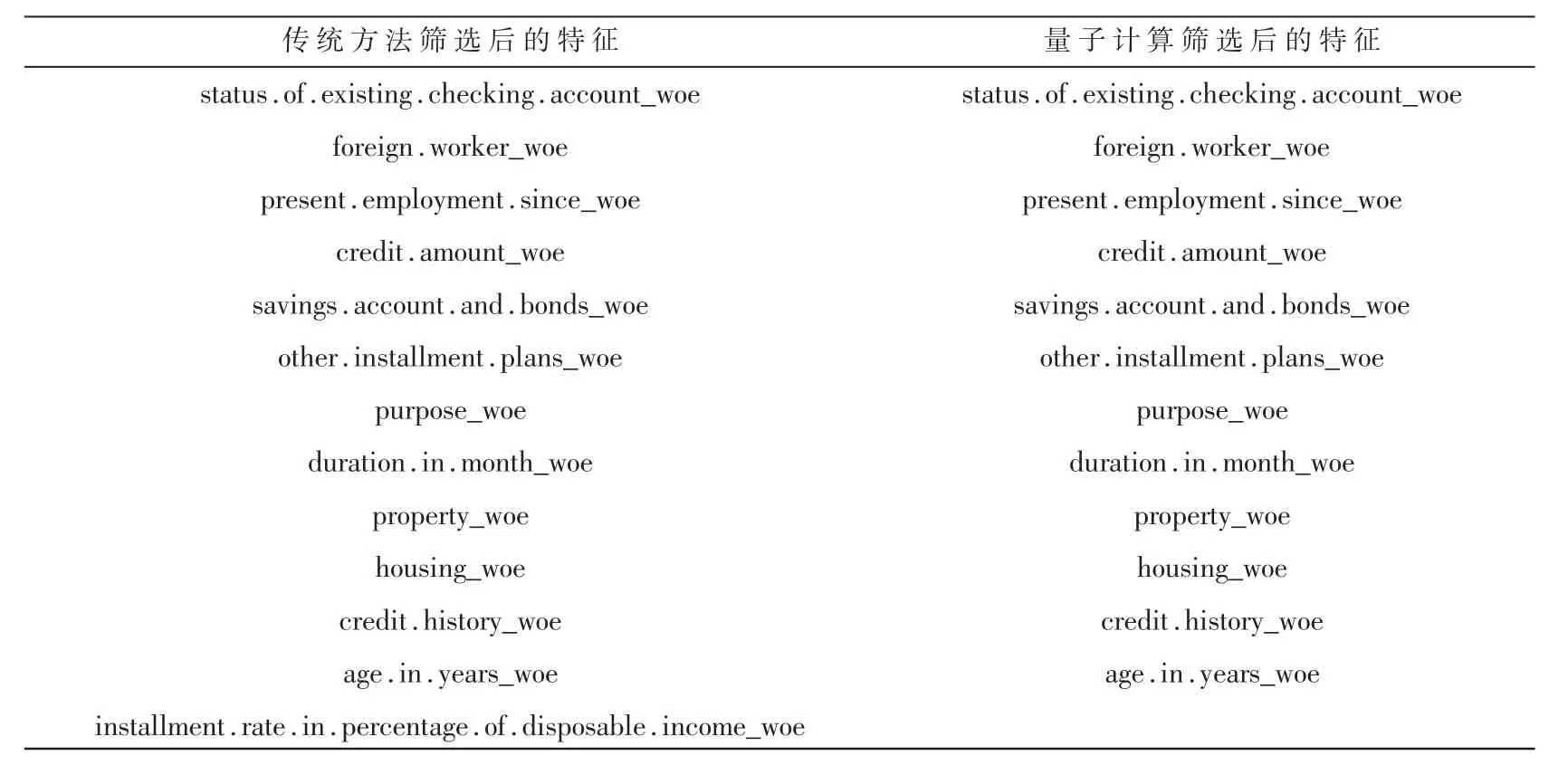
表1 传统筛选和量子筛选特征结果对比

3 评估指标及实验结果

信用评分模型的评估是通过未加权精度，即正确分类的数量除以分类的总数，对训练集和测试集的预测结果进行评分。

零规则：德国信用数据有700个0类样本(“良好信用”)和300个1类样本(“不良信用”)。因此，将所有样本分配给0类的“盲猜模型”将获得70%的成功率。

本文希望量子特征选择比零规则和随机选择的子集更好，结果可以媲美甚至超过传统的特征选择模型。在进行特征选择之前，首先确定逻辑回归模型在整个特征集上的表现，平均精度取决于数据被打乱的次数，以及数据如何在训练集和测试集之间进行分割。

选择1 000次洗牌和20%的测试份额的组合作为初始性能比较的标准。其他研究表明在德国信用数据上使用传统的特征选择准确性得分通常在70%～75%之间，标准差在5%左右。以下的实验结果均是基于1 000次洗牌和20%的测试份额的初始设置进行，并且根据K-S、ROC以及LR评判模型判断算法的好坏。

实验A：用one-hot编码对原始数据处理后获得的实验结果

图1中，图1(a)展示了K-S指标，其表示随着样本数(% of population)的增加，样本数中好的百分比和坏的百分比之间的差值的最大值；图1(b)展示了ROC曲线，阴影部分为AUC面积，代表了随着FPR的增加TPR的变化，AUC越接近1越好。这两个值经常用来评判模型区分样本好坏的程度。表2为具有48个特征的LR模型的准确率，表3为不同的超参数进行量子特征选择的结果。

图1 48个特征的LR模型的K-S和ROC

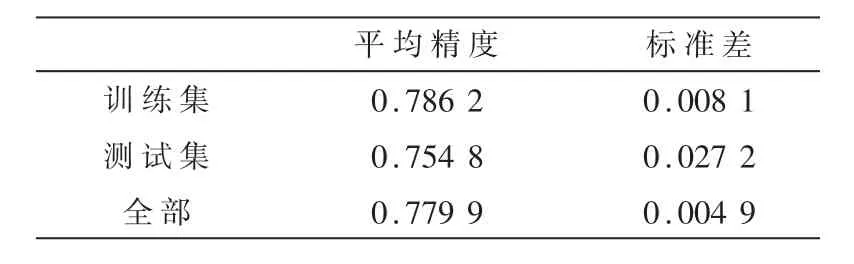
表2 具有48个特征的LR模型的准确率

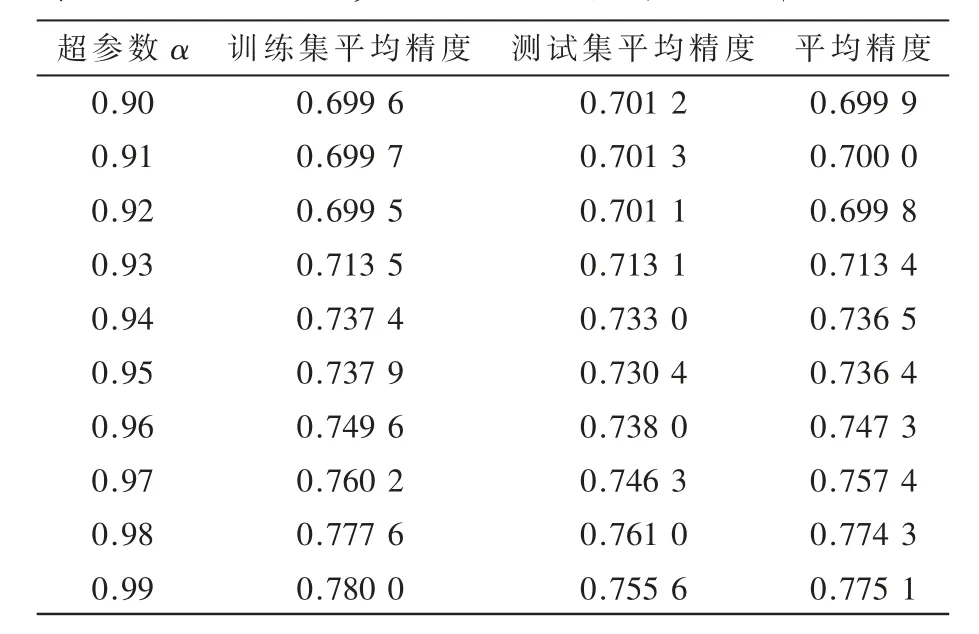
表3 不同的超参数进行量子特征选择的结果

不同的超参数进行量子特征选择的测试集结果如图2所示，考虑α≥0.9，精度高于零规则结果，从图2可以看到测试集的效果在α=0.98时达到较好的结果之后开始下降。α=0.98时模型的K-S和ROC如图3所示，α=0.98时进行量子特征选择后的模型准确率如表4所示。

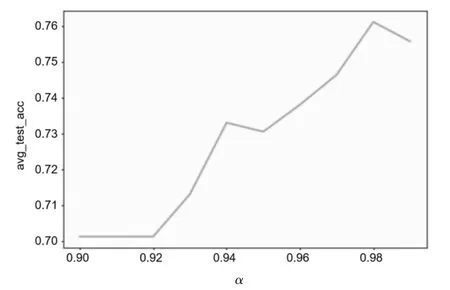
图2 不同的超参数进行量子特征选择的测试集结果

图3 α=0.98时模型的K-S和ROC

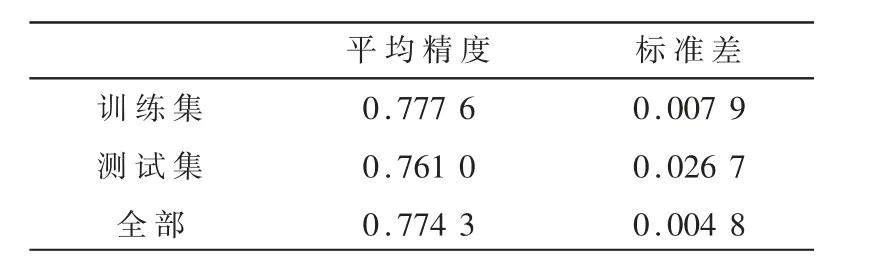
表4 α=0.98时进行量子特征选择后的模型准确率

实验B：用WOE分箱策略预处理数据，获得的实验结果如图4所示，全20个特征代入LR模型的模型准确率如表5所示，不同的超参数进行量子特征选择的结果如表6所示。

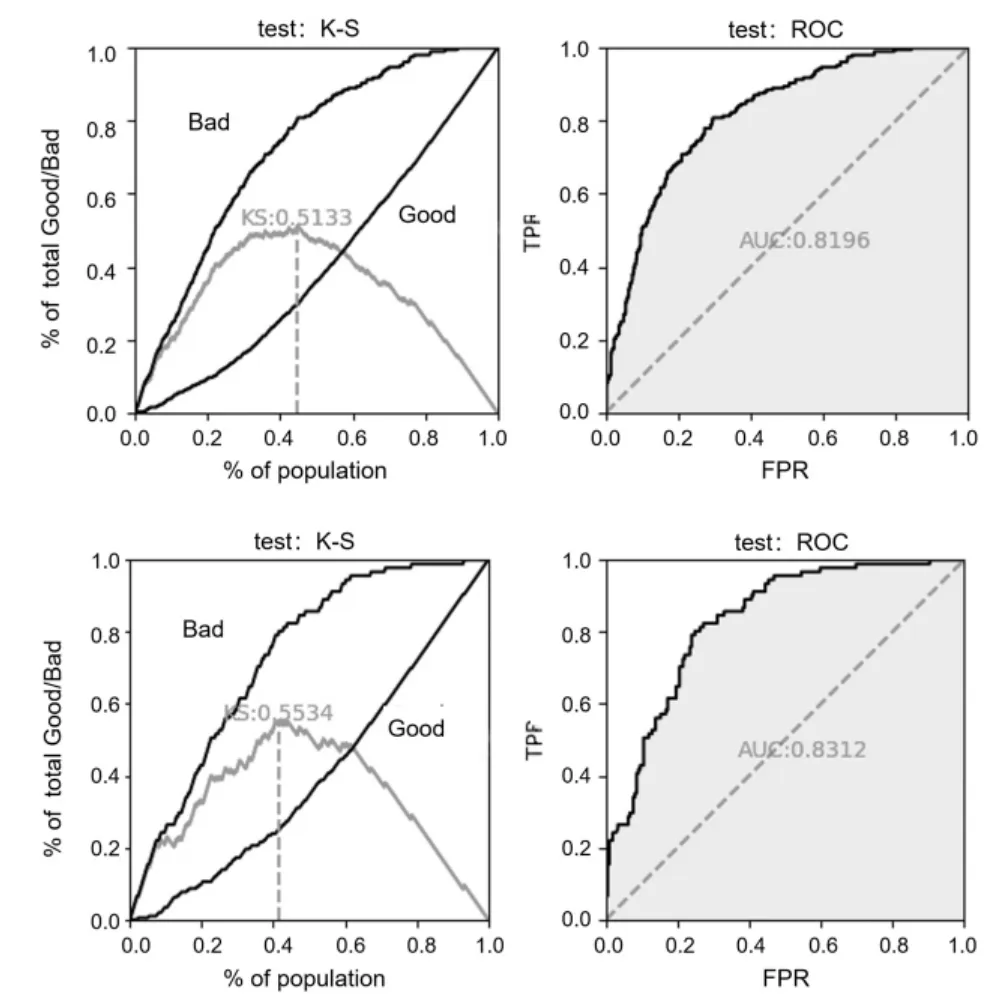
图4 全20个特征代入LR模型的K-S和ROC

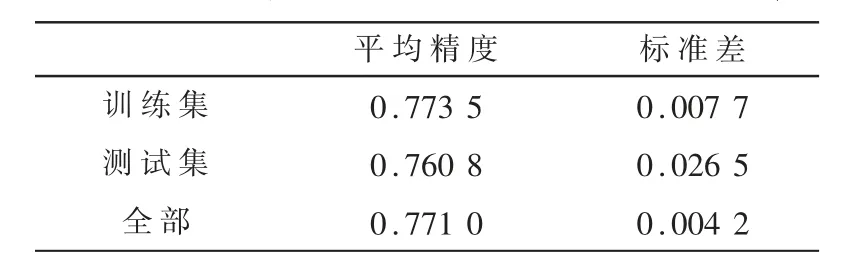
表5 全20个特征代入LR模型的模型准确率

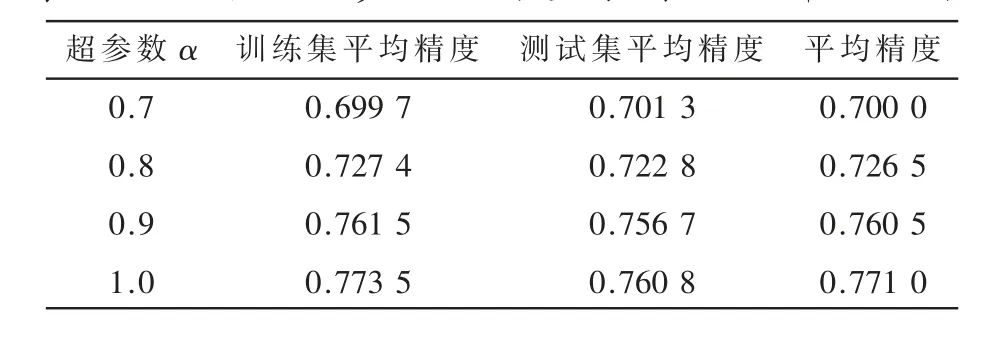
表6 不同的超参数进行量子特征选择的结果

更进一步得到α=0.98时，测试集的结果表现令人满意(如图5所示)，之后的精度增长趋于平缓。将选择的特征放入LR模型进行训练，结果如图6所示，20个特征用量子计算特征选择之后的模型准确率如表7所示。

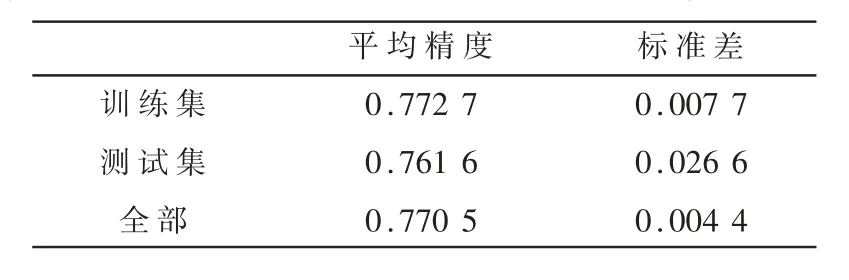
表7 α=0.98时进行量子特征选择的结果

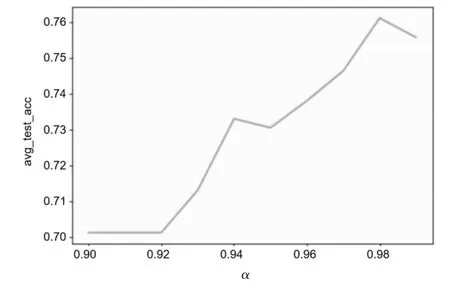
图5 不同的超参数进行量子特征选择的结果

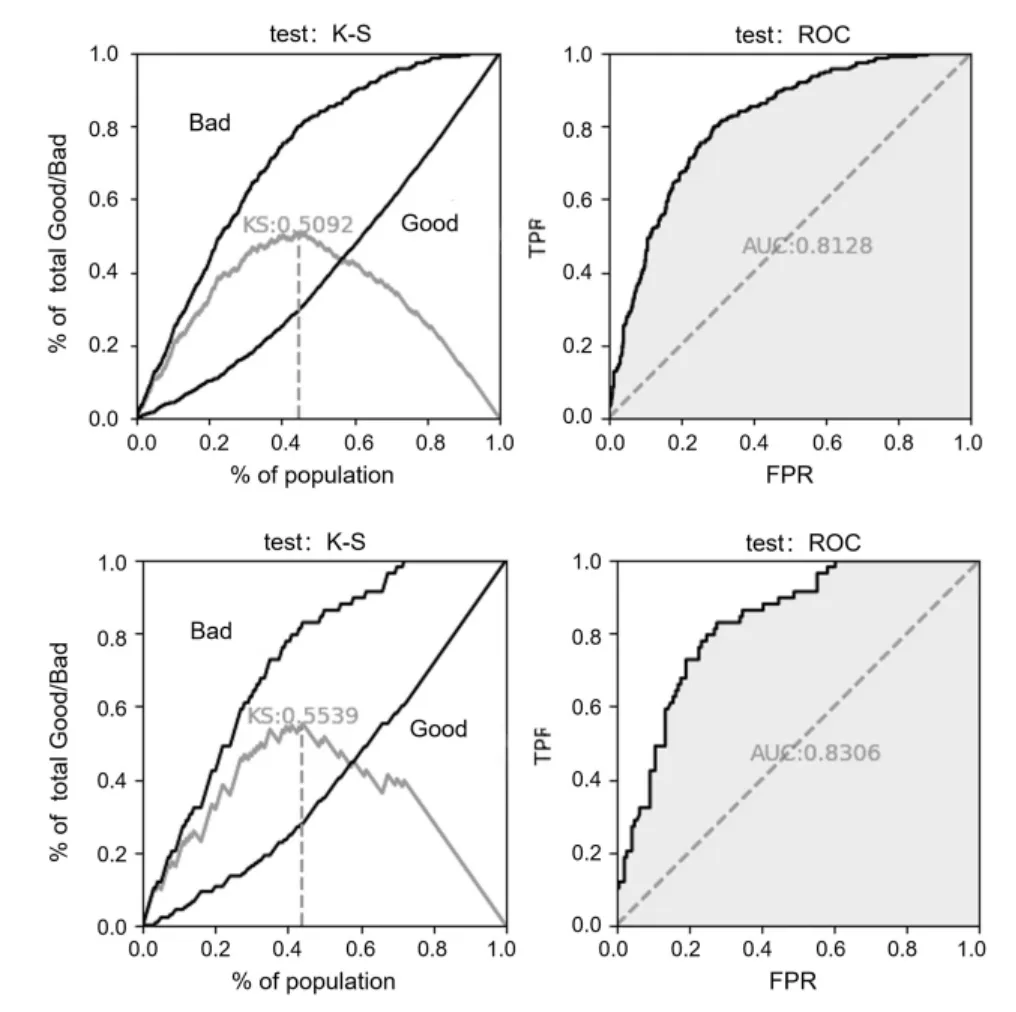
图6 α=0.98时特征筛选后模型的K-S和ROC

4 结论

在与传统的特征筛选方式进行对比后发现，本文采用的WOE策略与传统的one-hot编码相比，结果展示更为直观。通过量子计算方法筛选得到的特征与传统方法筛选的特征相比差别极小，在不降低准确率的情况下，基于量子计算的特征选取策略可以减少人为的参与，提高效率并降低对业务人员的依赖，从而减少操作风险。而在K-S以及ROC这两个评价模型中，量子计算策略是优于传统筛选策略；在LR评价模型中，量子计算策略和传统筛选策略效果近似。本文展示了量子计算应用于特征筛选该类特定问题上的可行性，尤其是面对特征数巨大的情况下，量子计算更显优势，其超越并替代传统方法的潜力巨大。

随着量子计算机和量子计算算法的发展，传统业务中的一些难题将迎来新的技术解决方案,例如计算成本较大、传统计算机的并行计算能力不高以及问题最优解优化不够等问题，都可以通过量子计算来解决。将量子计算运用到金融传统业务场景中的特定问题上，将是现阶段重点探讨和未来努力的方向。