改进的鲸鱼优化算法与图像阈值分割
郭松林, 巴艳坤
(黑龙江科技大学 电气与控制工程学院, 哈尔滨 150022)
0 引 言
鲸鱼优化算法[1](WOA)由于搜索能力强和收敛速度快等优点被广泛应用在工程领域的各个方面,但存在全局搜索能力差及寻优精度低等问题。基于此,国内外研究学者提出了诸多改进鲸鱼优化算法的方案,刘景森等[2]提出一种具有轮盘赌选择的双种群交互演化鲸鱼算法,但改进后的算法全局寻优能力和收敛性能仍有待改善。胡松等[3]通过引入自适应权重策略和天牛须搜索策略改进鲸鱼优化算法。肖爽等[4]将飞蛾-火焰算法融合到鲸鱼优化算法中,一定程度上可以预防算法早熟。余修武等[5]采用Levy飞行策略优化鲸鱼算法,提出了AWL-MC算法。为提高WOA的全局搜索能力,改善收敛性能,笔者提出改进鲸鱼算法的方案,采用Tent对算法的种群位置进行初始化,增强算法的多样性,将过渡参数由线性替换为非线性,以提升算法的局部收敛性能和全局勘探能力。
1 模型的建立
为增强鲸鱼算法的多样性,引入Tent混沌映射[6]初始化鲸鱼群体的位置,将线性过渡策略替换为非线性过渡,使算法从勘探到开发的过程更加合理。
1.1 鲸鱼优化算法
鲸鱼优化算法是对鲸鱼围捕猎物的行为进行模拟。鲸鱼群主要通过包围猎物和用汽泡网驱赶猎物,在每次迭代中,鲸鱼群会随机选择一种行为进行捕猎。
(1)包围猎物
鲸鱼群随机选择向着最优位置或随机位置进行移动,对猎物进行包围。
向着最优位置的鲸鱼游动
(1)
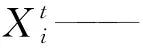
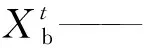
A——均匀分布(-a,a)的随机数,a的初始值为2;
C——均匀分布在(0,2)内的随机数。
向着随机位置的鲸鱼游动
(2)
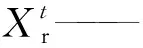
(2)气泡网捕猎
(3)
式中:m——常数;
l——[-1,1]的均匀随机数。
1.2 Tent混沌映射
混沌现象是一种普遍存在的自然现象,混沌变量具有遍历的特性[7],因此在算法中加入混沌映射可以增强算法多样性,提高算法的全局搜索能力,常见的有Logistic映射和Tent映射如图1所示。由图1可以看出,Logistic映射的取值主要分布在[0,0.05]和[0.9,1.0]两个区间内,因此Logistic遍历具有不均匀性。单梁等[8-9]研究表明,Tent映射与Logistic映射相比,取值分布更均匀,遍历性更强,证明了Tent映射可以作为产生优化算法的混沌序列。
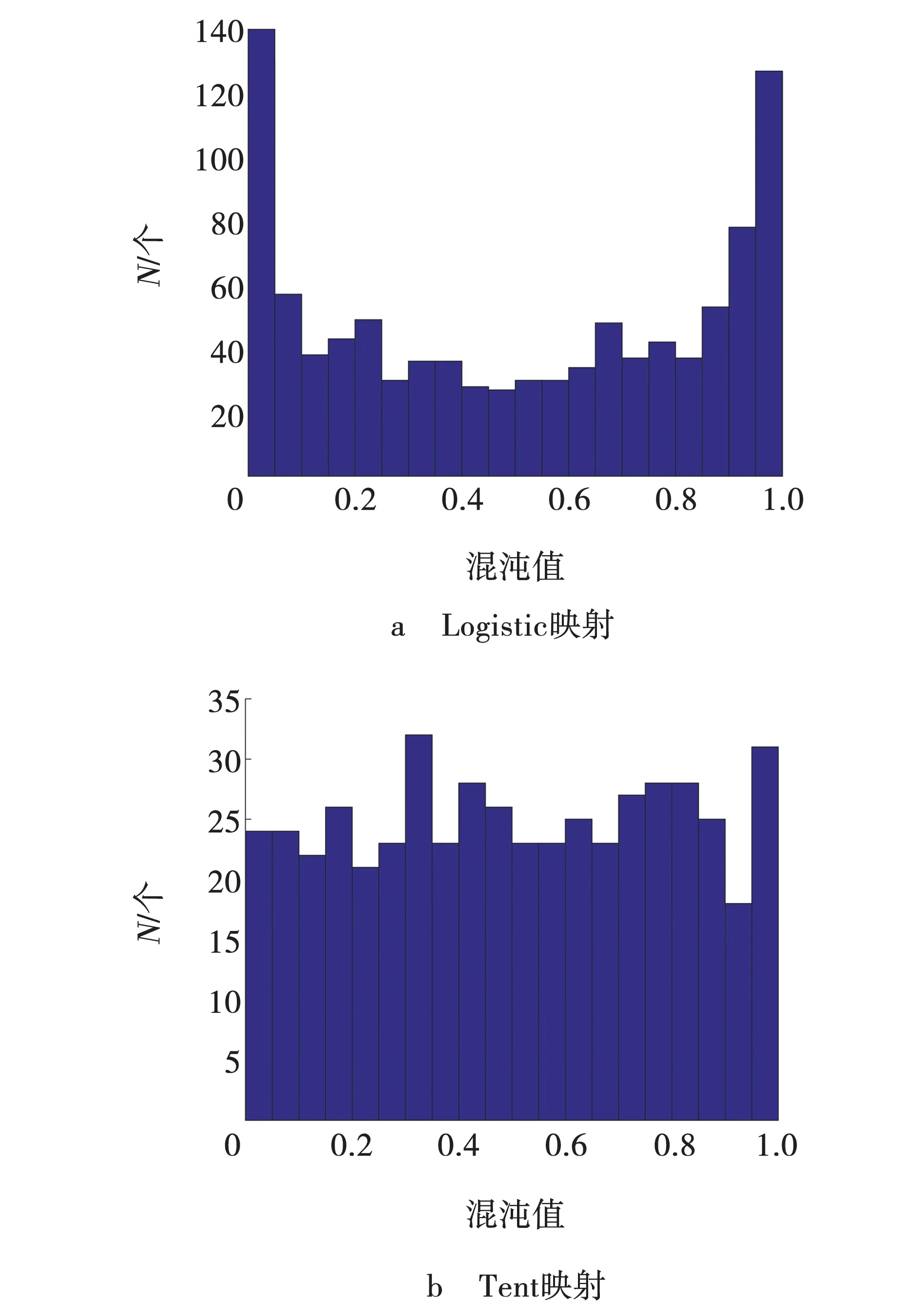
图1 混沌映射直方图Fig. 1 Histogram of chaotic map
Tent映射表达式为
(4)
式中,i——第i维。
1.3 正弦函数的非线性过渡参数
收敛速度和种群多样性是影响算法的主要因素。在传统鲸鱼算法中,式(1)中的过渡参数a决定了算法在多样性和收敛性之间的协调能力。若a>1时,进行全局勘探;反之,进行局部寻优,因此对于a值的选择是否合适至关重要。由式(1)和(2)可知,a是线性递减的,而优化问题多是非线性变化的,因此,合理地设置参数a,能够很好地改善WOA算法的性能。吕鑫等[9-10]研究表明,算法进行搜索的过程是非常复杂的,整体来讲,呈非线性变化的趋势,因此传统鲸鱼算法中的a并不能真实全面地反映出算法的优化搜索过程,从全局勘探到局部开发也不能形成良好过渡。对此,徐明等[11]提出一种非线性过渡策略为
(5)
式中:amax、amin——a的最大值和最小值;
t——当前迭代次数;
T——算法最大迭代次数。
WOA同样具有局部搜索能力强而全局搜索能力弱的特点,因此,利用式(5)对过渡参数a进行改进。式(1)中的收敛因子a线性递减策略和非线性递减策略的比较如图2所示。

图2 过渡参数的比较Fig. 2 Comparison of transition parameters
2 改进算法性能测试
2.1 改进的鲸鱼优化算法
改进鲸鱼优化算法,分为以下五个步骤。
步骤一初始化,种群规模N,目标函数维度d,上、下界ub和lb,最大迭代次数T。
步骤二使用Tent混沌序列初始化种群。
步骤三利用非线性过渡参数a替换掉先行过渡参数。
步骤四更新各鲸鱼的位置,计算各鲸鱼的适应度,找出最优位置的鲸鱼和适应度。
步骤五判断适应度值是否满足条件或达到设定迭代次数,若是,则结束;若否,则返回步骤四。
2.2 改进的鲸鱼优化算法性能测试
选取8个基准函数测试改进鲸鱼算法的性能,将改进鲸鱼优化算法(IWOA)的寻优结果与PSO、WOA和GWO的寻优结果进行对比分析,各算法的参数设置相同,分别运行30次,取所有运行次数结果的平均值和均方差作为评估指标。
单峰值测试函数f1、f2和f3分别为
高维多峰值测试函数f4、f5和f6分别为
固定维多峰值测试函数f7和f8分别为
f1、f2、f3、f4、f5和f6的理论最优解除f4外均为0,维度均为30。f7和f8为固定维多峰函数,维度分别为2和4,理论最优解分别为1和-10.536 3。
表1~3为各算法对函数进行寻优测试后统计结果,在对f1、f4和f6进行寻优测试时,IWOA均可找到最优解,标准WOA仅在对f4和f6进行寻优时,可以找到最优解,PSO和GWO无法找到全局最优解;在对f2、f3、f5、f7和f8函数进行寻优测试时,IWOA寻优结果在4个测试算法中均位居第一,且通过算法测试的标准差可以看出,IWOA收敛值的分布更加集中,寻优结果更加稳定。
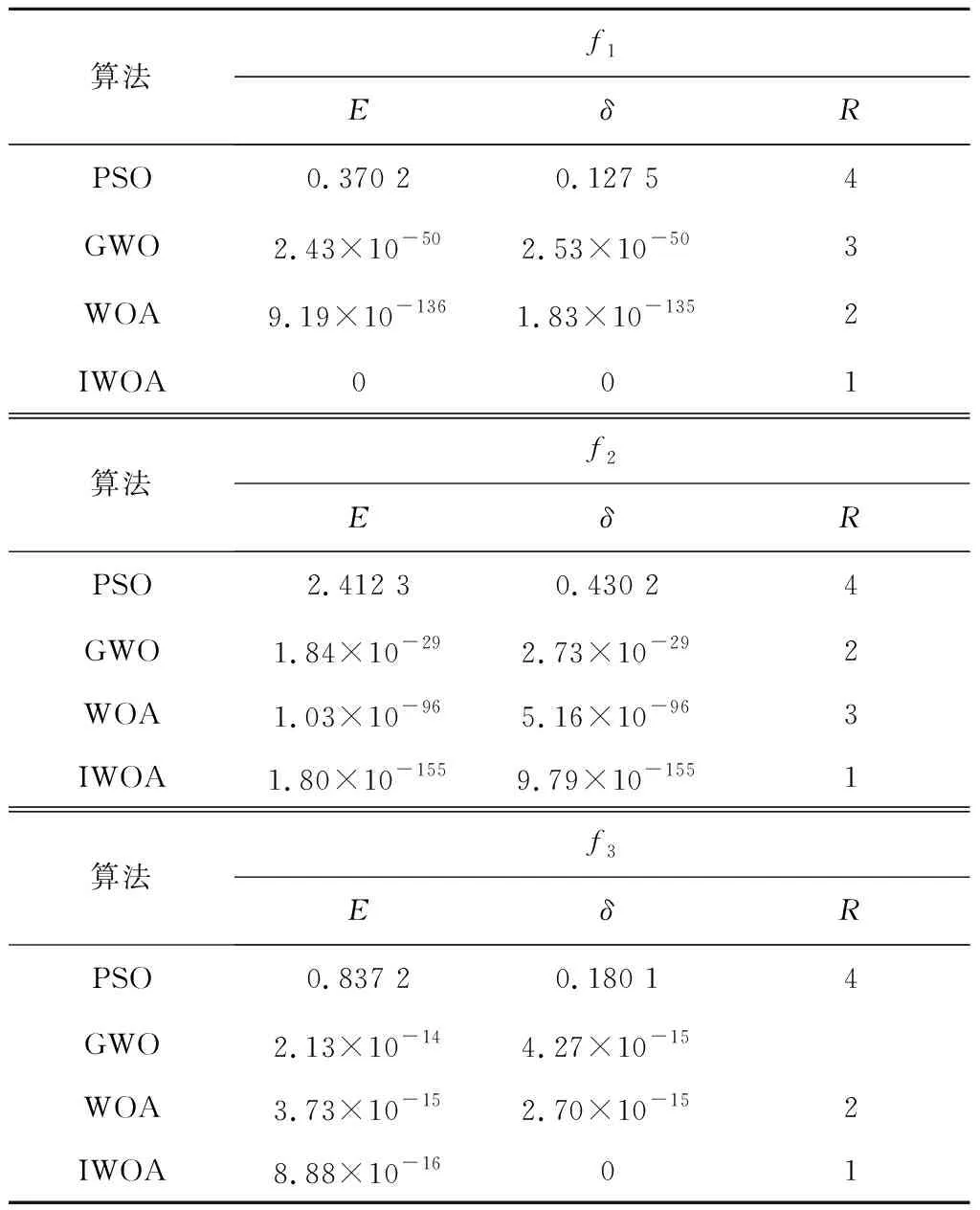
表1 不同算法对单峰值测试函数寻优结果
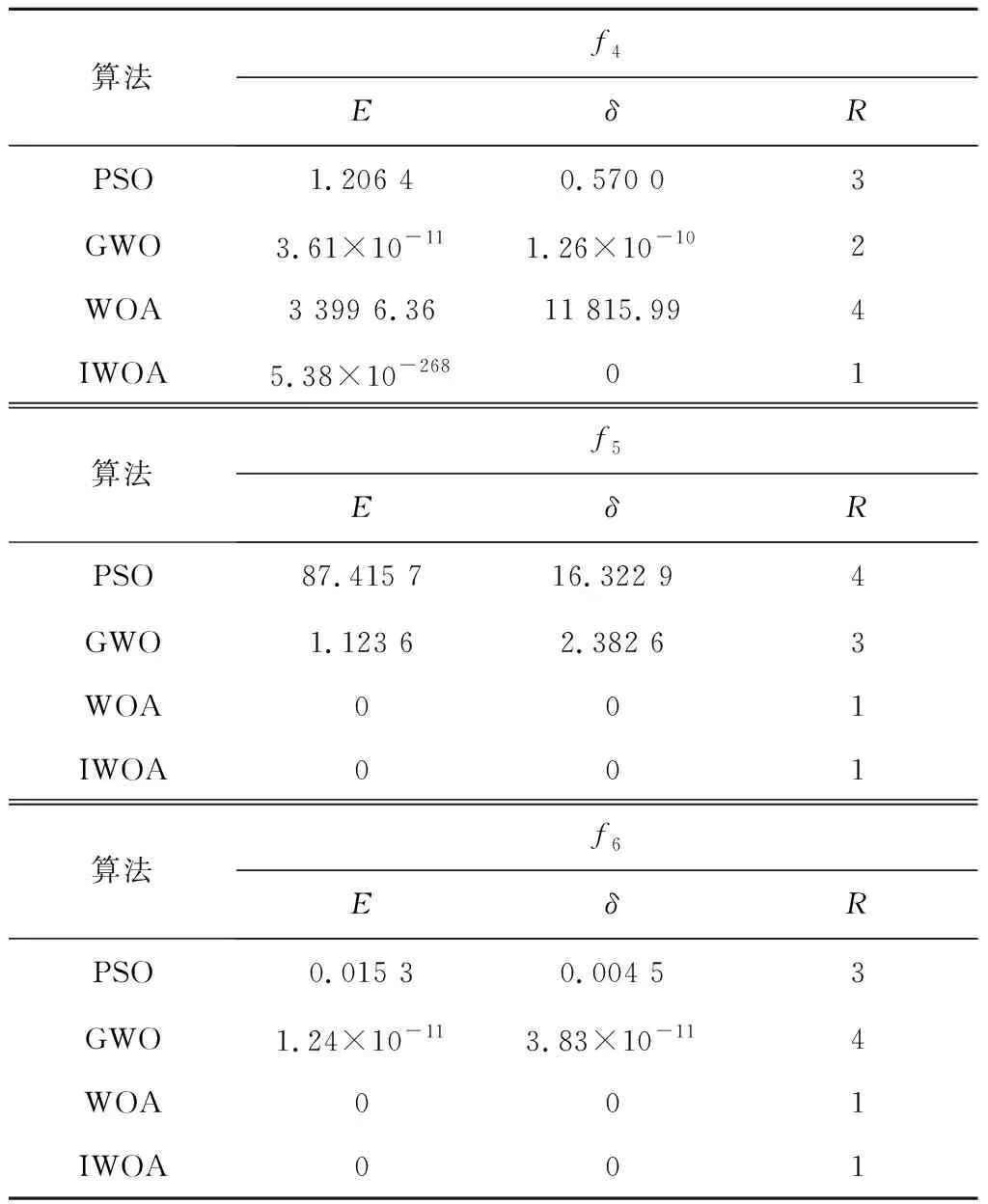
表2 不同算法对高维多峰测试函数寻优结果
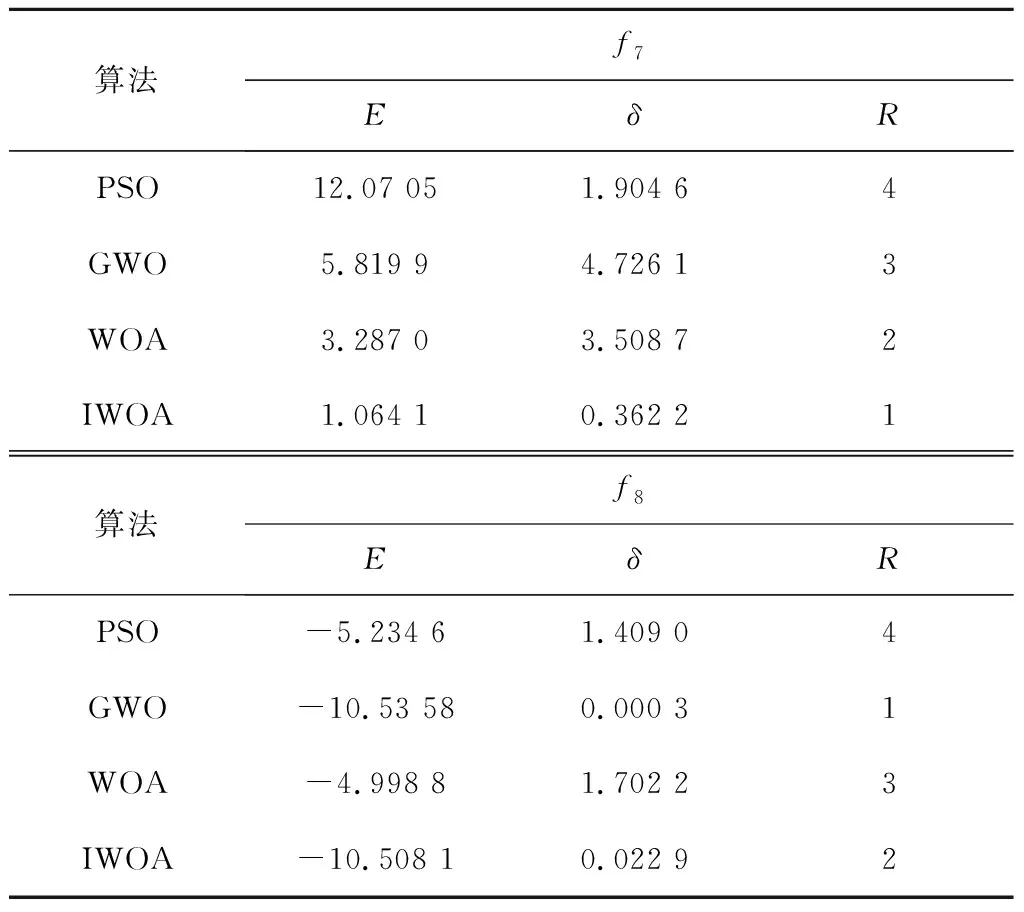
表3 不同算法对固定维多峰测试函数寻优结果
各算法对测试函数进行寻优测试的收敛性能曲线如图3~5所示。为了进一步验证改进后算法的性能,对IWOA进行秩和检验,将所有测试值按照从小到大的次序排列,并将各个测试值按照排列的顺序进行编号,称为秩,分别对两组的测试值计算秩和进行检验,如表4所示。
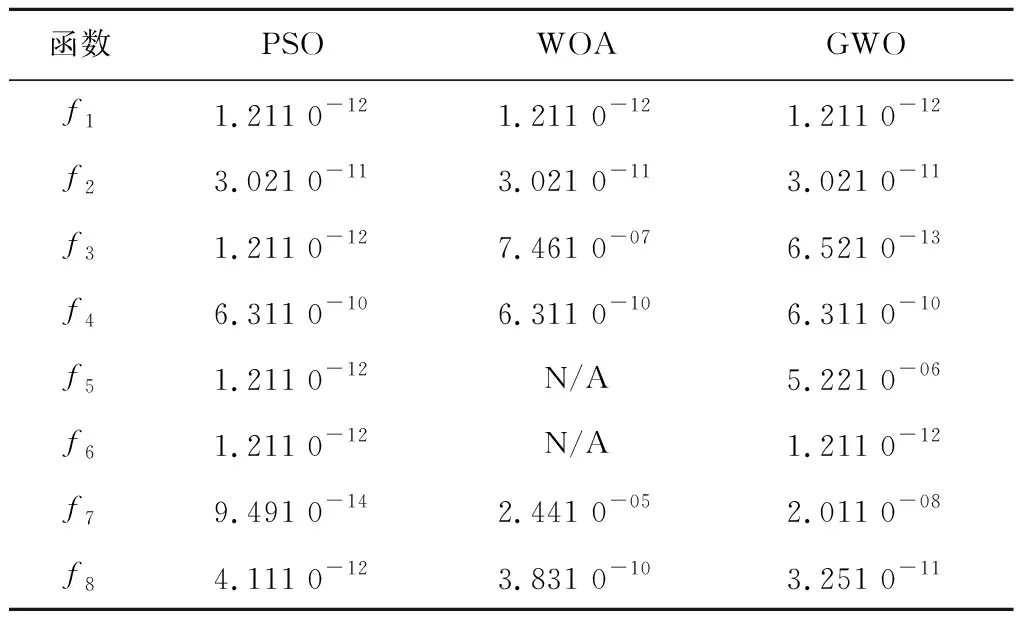
表4 Wilxocon秩和检验
由图3~5可以看出,在对f1、f3、f5、f7和f8函数进行寻优测试时,IWOA的收敛性能均优于PSO、WOA和GWO;对f2函数进行寻优测试时,在5次迭代之后,IWOA的收敛速度明显加快,且寻优精度远优于PSO、WOA和GWO;对f4函数进行寻优测试时,在20次迭代之前,PSO寻优精度优于IWOA,但在20次迭代之后,IWOA明显优于其他3个算法;对f6函数进行寻优测试时,在10次迭代之前,PSO寻优性能优于IWOA,但在10次迭代之后,IWOA明显优于其他3个算法。
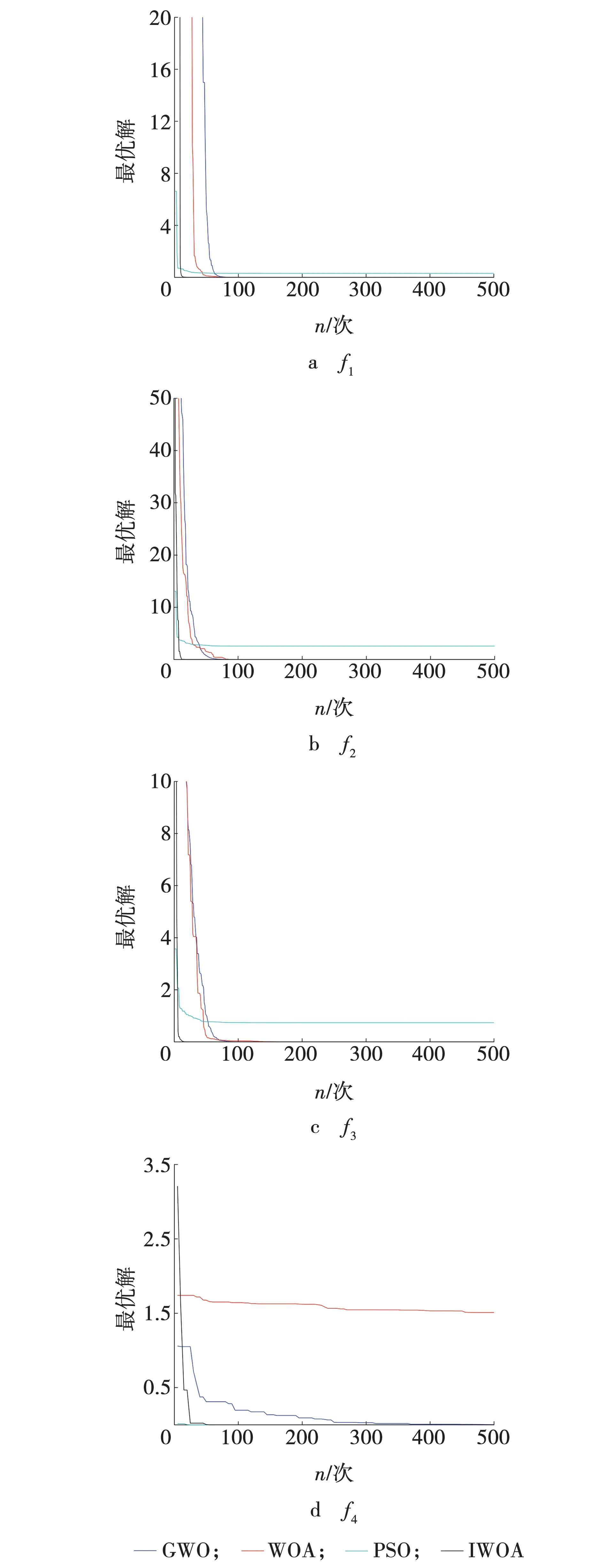
图3 各算法对f1~f3的寻优收敛曲线 Fig. 3 Optimization convergence curve of each algorithm for f1-f3
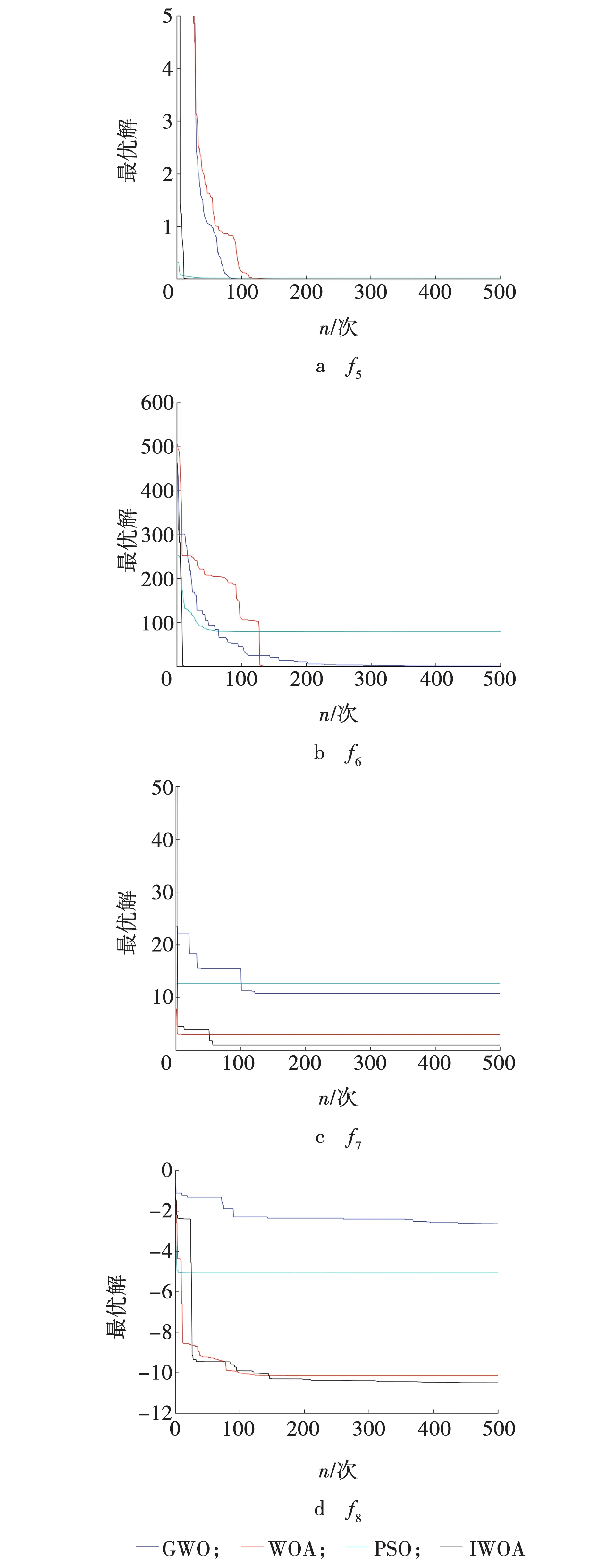
图4 各算法对f4~f6的寻优收敛曲线Fig. 4 Optimization convergence curve of each algorithm for f4-f6
仿真结果表明,在对WOA进行改进后,算法的收敛性能得到显著提升,通测试结果的标准差可知,IWOA的收敛更加稳定。
在p=5%显著水平下进行检验,若显著水平p<5%,则认为两算法之间具有显著差异;若显著水平p>5%,则认为两算法之间没有显著差异,即两算法性能相当。
由表4可以看出,IWOA在8个测试函数上均优于PSO和GWO,在6个测试函数上优于WOA。结果表明,IWOA与其他三个算法存在显著性差异。
3 工程应用
图像分割问题是实际工程中常见的一类问题,通过图像分割验证改进后算法能否应用在实际工程中。
对图像进行二值化处理最有效和最常用的算法是大津法[9],将图像分为前景和背景,找到能使类间方差最大的分割阈值即为最佳阈值,在图像分割中IWOA的适应度函数为
f(x,y)=x1x2(y1-y2)2,
(6)
式中:x1——前景图像所占图像的比例;
x2——背景图像所占图像的比例;
y1——前景图像的平均灰度;
y2——背景图像的平均灰度。
采用IWOA对图像进行阈值分割,即找到一个最优位置作为分割阈值,使类间方差最大。种群规模设置为20,最大迭代次数设置为100,目标函数的维度设置为1,初始值上下界分别设置为255和0。运行30次后分割阈值的最大值、最小值、平均值和标准差如表5所示。
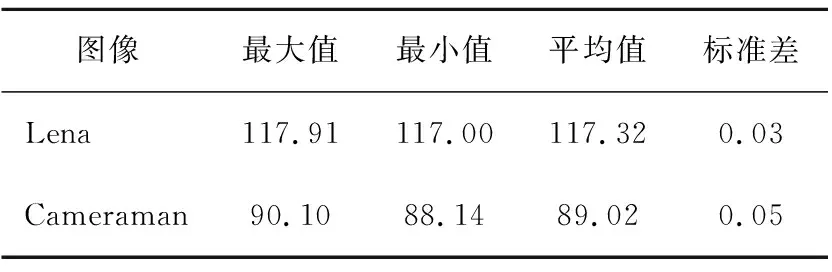
表5 图像分割阈值
由表5可知,IWOA进行图像分割得到的最优分割阈值,而使用大津法进行图像分割得到的最优分割阈值分别为89和117。由表5可以看出,通过IWOA得到的结果分布在大津法得到的结果周围,收敛效果显著。图5和6为大津法和IWOA进行图像分割的结果,从图5、6可以看出,IWOA和大津法分割结果相似,因此IWOA实际工程问题的应用中切实可行。

图5 Lena标准测试图像Fig. 5 Lena standard test image

图6 Cameraman标准测试图像Fig. 6 Cameraman standard test image
4 结 论
(1)采用Tent混沌映射初始化鲸鱼个体的位置,增强了算法的种群多样性,将线性过渡参数改为非线性过渡,提高了算法的全局搜索能力。
(2)通过测试结果的平均值和标准差可知,IWOA寻优精度更高,稳定性更强,收敛值分布更集中,寻优结果更加稳定。
(3)将IWOA应用到图像分割问题中,与大津算法得到的结果相比,平均误差为0.15%,在图像阈值分割的工程标准范围之内,验证了其在工程领域应用的可行性。

