耦合温度衰减效应的月球光伏板倾角优化设计

潘浩丹 徐第开 樊 帆 朱亚著 钱 华 赵东亮

(东南大学能源与环境学院， 南京 210096)

2007年，中国“嫦娥一号”成功发射并实现绕月探测.此后，中国多次发射探月卫星，并于2020年成功完成了“绕、落、回”的第一阶段探月总规划[1]，下一阶段规划为“勘、研、建”，其旨在利用月球原位能源，使人类能够长期驻守月球.太阳能作为月面最可靠的原位能源之一而备受关注，由于月面气压约为0.3 nPa[2]，接近真空，太阳辐射不会受到大气的削弱，因此太阳能光伏技术成为月面探测与建设的关键技术[3-4].近年来，光伏技术取得了显著的突破[5]，Ⅲ-Ⅳ族砷化镓光伏板已广泛应用于航空领域[6-8]，如嫦娥系列探测器[9]、国际空间站[10-11]均搭载Ⅲ-Ⅳ族砷化镓光伏板.目前，国内外已实现光电转换效率达30%的多结光伏电池的量产[12-13]，光伏技术的日趋成熟为人类高效利用月面太阳能提供了有利条件.最初，Landis等[3]于1990年提出了基本的月面光伏系统构想，但仅仅通过太阳高度角0°～90°的线性假设设计月球光伏板的倾角、朝向等参数，该处理忽略了月球独特的太阳空间变化规律且更多集中于定性分析.此后，Kaczmarzyk等[14-15]采用适用于地球的经验公式计算太阳高度角、月面太阳辐射强度等，该近似处理初步构建了月面光伏系统的理论框架，但仍缺乏月面太阳辐射环境的针对性设计，无法表征真实的月球工况.此外，太阳辐射为月面的唯一外部热源[16]，对月面温度影响重大.现有研究表明，月球赤道地区的表面温度在日间可达到400 K以上[17]，而在纬度较高的月球极区，日间表面温度普遍在160 K左右[18-19]，由此可见不同纬度带来了月面温度的巨大差异[20-21].文献[22]表明，“嫦娥”、“玉兔”系列月球车需要通过“月午休眠”保护其科学负载不受月面中、低纬度区域的月球日间强红外辐射高温的危害，证实月面高温引发的问题实际存在.对于光伏板，温度是其发电效率的重要影响因素，过高的工作温度将导致光伏板发电效率衰减.然而，以往的月面光伏系统研究中并没有考虑月面日间温度的纬度差异[3-4]，忽略了温度这一关键因素对光伏系统的影响，无法实现不同纬度月面光伏系统的效益最大化.

光伏板接收的太阳入射辐射能量由当地太阳辐射条件与光伏板朝向和倾斜角度决定，因此设计光伏板的朝向和倾斜角度是提升光伏效率的核心步骤.时刻跟踪太阳轨迹的光伏系统可以使光伏板最大化地接收太阳辐射能量，然而跟踪系统的运行需要额外能量与运动部件，因此降低了太阳轨迹跟踪系统的运行可靠性和稳定性[23].考虑到月球人工系统对稳定性的特殊要求，本文采用固定倾斜角度与朝向的月面光伏系统.针对地球光伏系统的研究表明，光伏板的散热主要由自然对流承担[24-25]，换热条件相对优异，因此合理的倾斜角度和朝向更聚焦于使光伏板最大程度地接收太阳辐射，以输入能量最大化为设计目标，即输入特性导向型算法；而对于月球表面以辐射换热为主的热环境，光伏板散热途径相对匮乏，最大程度接收太阳辐射意味着光伏板的温度也将大幅升高，光伏板的过热必然导致光伏发电效率的衰减.此外，不同倾斜角度对应不同的辐射换热角系数也将影响光伏板与月面的辐射换热从而作用于发电效率，因此光伏板倾斜角度是决定月面光伏板发电效率的核心因素.综上，针对月球光伏系统，光伏板倾斜角度与朝向的确定应将光伏板的温度衰减效应纳入计算，权衡分析光伏板接收的太阳辐射总量与光伏板温度之间的关系，以输出能量最大化为设计目标.

本文基于Variations Séculaires des Orbites Planétaires (VSOP)[26-27]与Éphéméride Lunaire Parisienne (ELP)[28-29]半解析轨迹理论建立月球轨道模型，该2种理论考虑了行星轨迹细微偏移，具有较高的预测精度并且适用范围较广.以此得到月面各纬度精确的太阳辐射条件，包括月面太阳高度角、月面太阳方位角、月面太阳辐射强度，随后通过构建光伏板、月面、太阳三者的辐射换热模型计算各纬度下不同倾斜角度与朝向的光伏板温度，据此分析光伏板输入特性与输出特性的纬度变化规律，并提出了耦合温度衰减效应的输出特性导向型光伏板最优倾斜角度的优化算法，以此为基础探究月面不同纬度下单位面积最大可输出电能的分布规律.

1 月面光伏板换热模型

首先根据月球轨道模型计算月面太阳辐射常数Em与月面任意位置的太阳高度角Hs，以此计算任意位置的月面温度TG与不同朝向及倾斜角度下光伏板的太阳入射辐射量IT，并构建光伏板温度Tcell、位于光伏板阴影中的月面温度TG_back、光伏板实际效率ηreal三者之间的耦合关系，最终计算输出特性导向型的光伏板最优倾斜角度βopt、朝向角度γs_opt以及该条件下的最大单位面积可输出电能Emax.

在上述计算中采用了如下假设：①为得到光伏板倾斜角度随纬度变化的普适性规律，假设月球为理想球体，不考虑月面高程对太阳辐射的影响[14,30-31]；②参考Liu等[32]和Duffie等[33]提出的分析方法，将换热系统简化为二维系统，并假设月面为漫射体，如图1所示，其中S1为太阳照射下的月面，S2为光伏板，S3为位于光伏板阴影中的月面；③考虑到月尘的高静电吸附、易长期悬浮等不利特质[20,34]，为了预留充足的清理通道，假设光伏板前后间距D远大于光伏板长度L，前后光伏阵列温度场互不影响且无遮挡作用，即每块光伏板为独立的计算单元，如图1(b)所示；④Ⅲ-Ⅳ族砷化镓薄膜光伏板厚度远小于其他方向上的尺寸[6-7,12-13,35]，忽略厚度方向温度梯度.

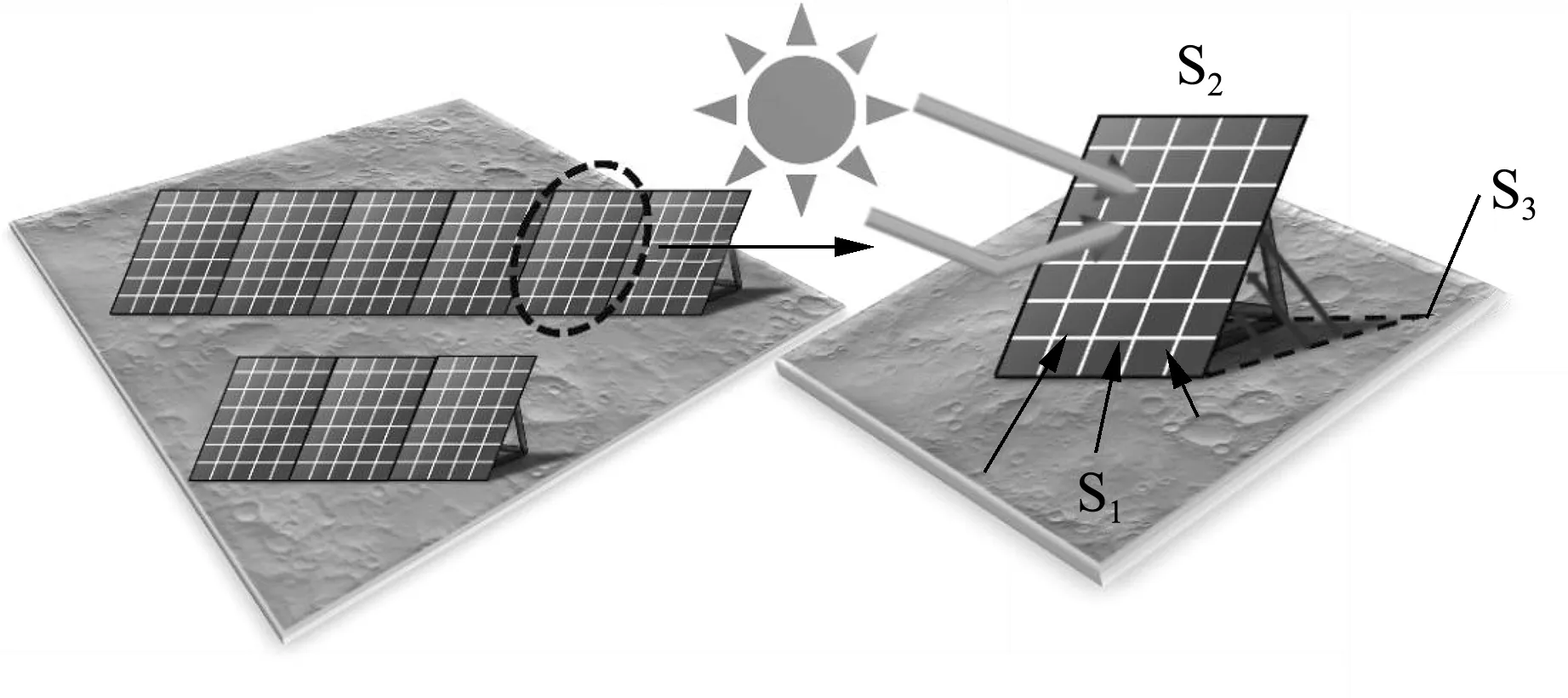
(a) 光伏阵列示意图

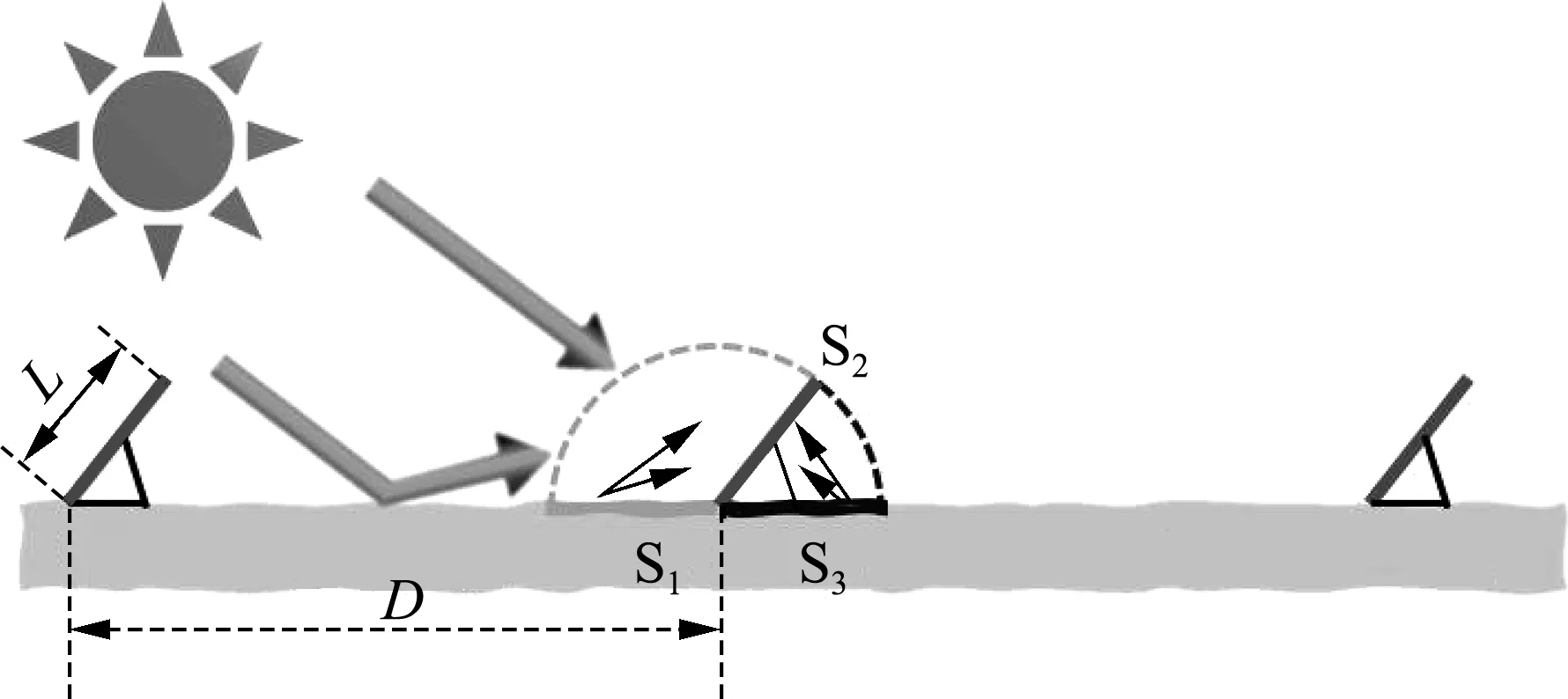
(b) 光伏板、月面、太阳辐射换热模型示意图

1.1 太阳高度角、方位角以及辐射常数计算

计算月面任意位置的太阳辐射强度首先需要计算月球表面太阳辐射常数Em.日、地、月三球系统如图2所示，其中黄道面指地球绕太阳公转的轨道平面，白道面指月球绕地球公转的轨道平面.存在以下关系[31]：

(1)

(2)

(3)

式中，S0为地球太阳辐射常数，W/m2；Rsm为相对于1 A.U.(149 597 870 700 m)的无量纲日月距离；Rem为无量纲地月距离；Wem为月球的地心黄纬，°；Wsm为月球的日心黄纬，°；Rse为无量纲日地距离.

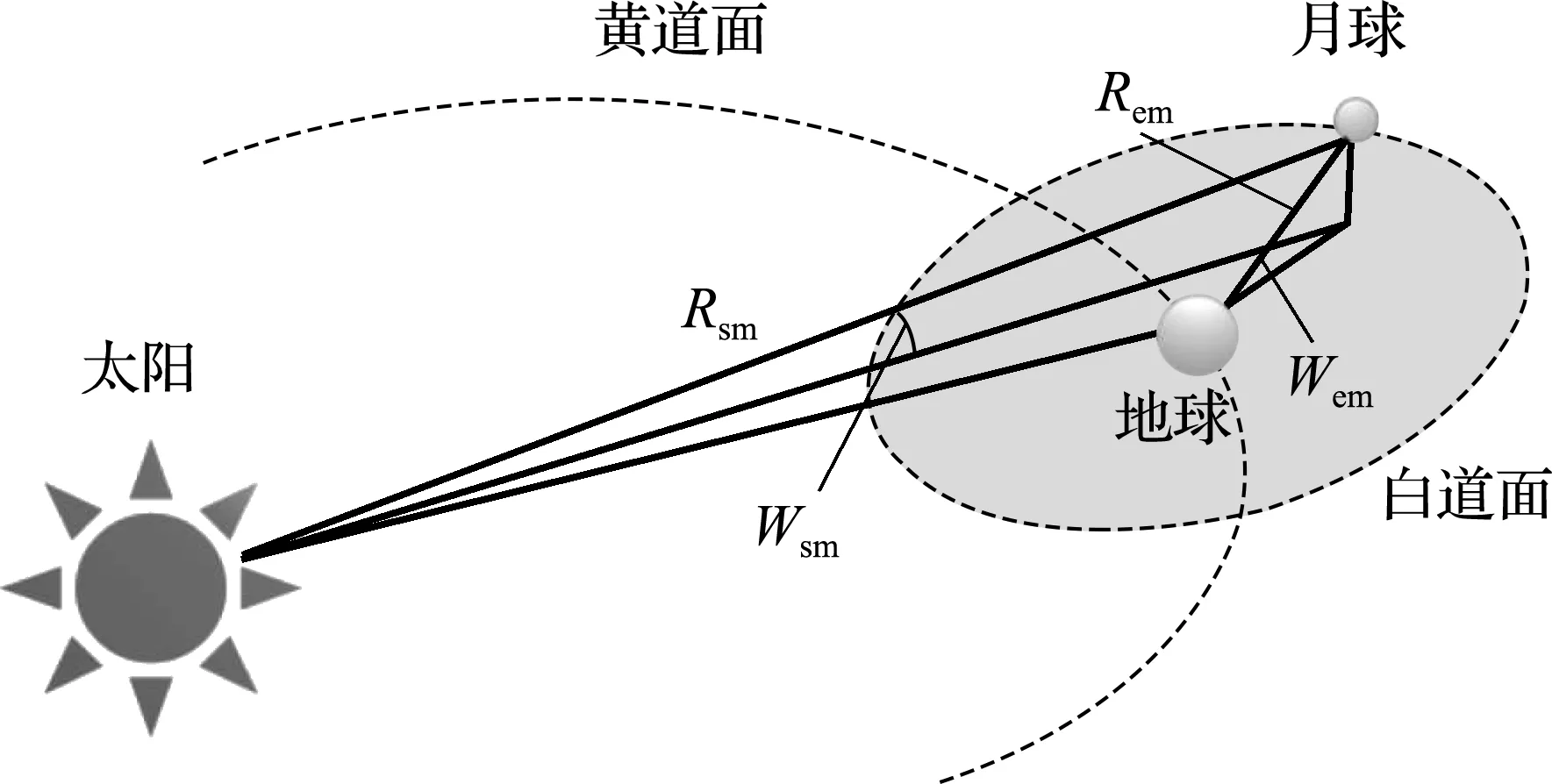
图2 日、地、月三球系统示意图

根据天平动理论[36]以及上述日、地、月之间的星体关系[37]可得到月面的太阳直射点位置(φs,λs)，并以此计算月面太阳的高度角Hs、方位角As.日、月双球系统的几何关系如图3所示，Hs与As可按下式计算[31,37]：

Hs=90°-α′-β′

(4)

(5)

式中，(φm,λm)为观测点的位置坐标；α′与β′为角度系数，计算公式为

β′=arccos[cosφmcosφscos(λm-λs)+sinφmsinφs]

(6)

(7)

式中，R为月球的平均半径[2]，m.

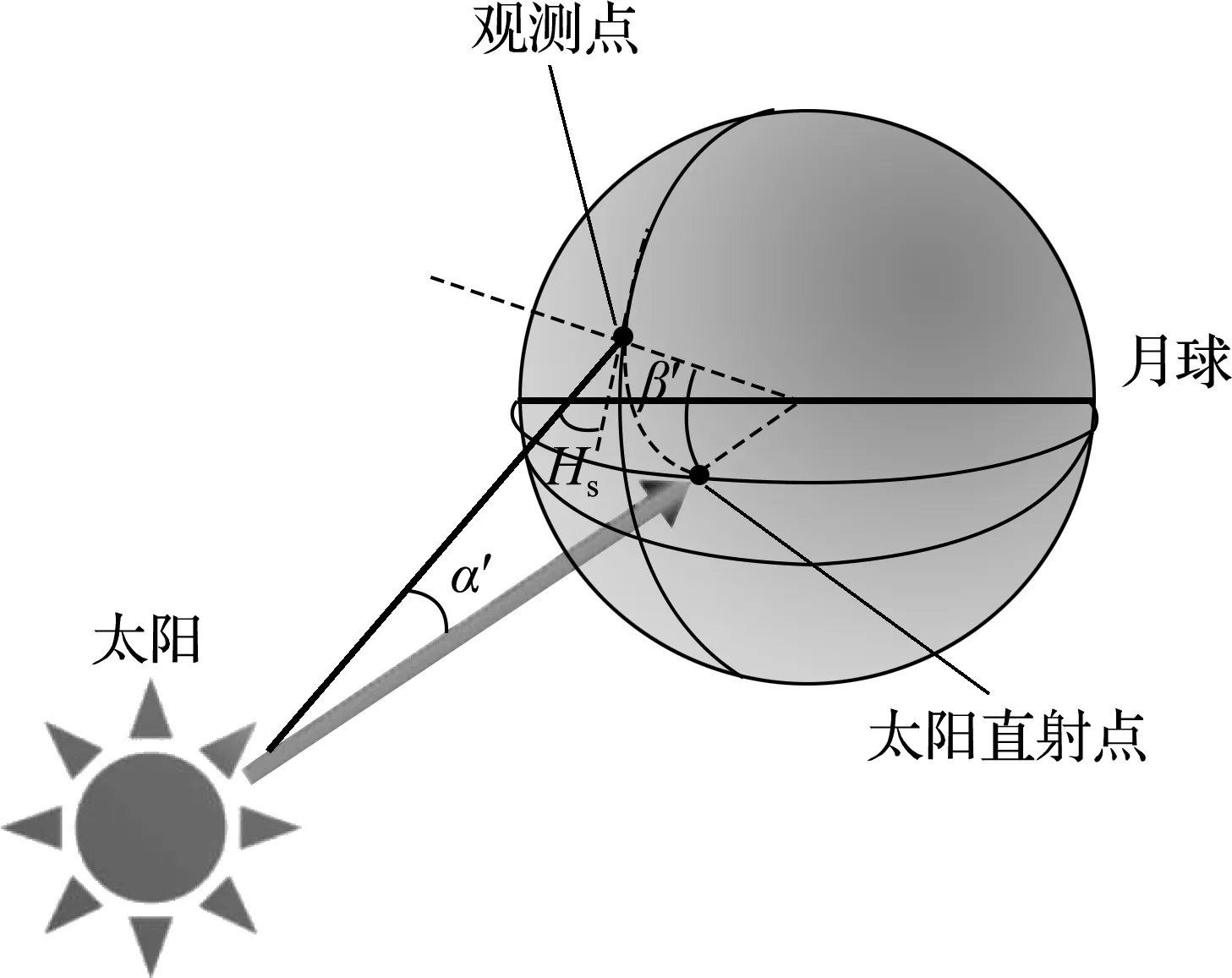
图3 日、月双球系统示意图

1.2 月面温度与光伏板太阳入射辐射量计算

月球表面温度采用月面稳态温度公式[38]进行计算：

(8)

式中，ρ为月球表面可见光反射率，取ρ=0.127[39]；ε为月球表面红外发射率[30,38]，取ε=0.97；M为深层月面的冷却能量密度，取M=6 W/m2[38]；σ=5.67×10-8为斯特潘-玻尔兹曼常数.

在光伏板表面，太阳入射辐射量IT包括太阳直接辐射量IB与月面反射太阳辐射量IR.太阳辐射与光伏板的几何关系如图4所示，图中，α为太阳辐射的水平分量与光伏板法平面在水平面上投影的夹角；β为光伏板倾斜角度；γs为朝向角度，表示光伏板法平面在水平面上的投影与东西方向的夹角，即当光伏板朝向赤道时γs=90°，光伏板朝向东边时γs=0°，光伏板朝向西边时γs=180°.太阳入射辐射量计算式为

IT=IB+IR

(9)

IB=Ivcosβ+Ihsinβ

(10)

Iv=EmsinHs

(11)

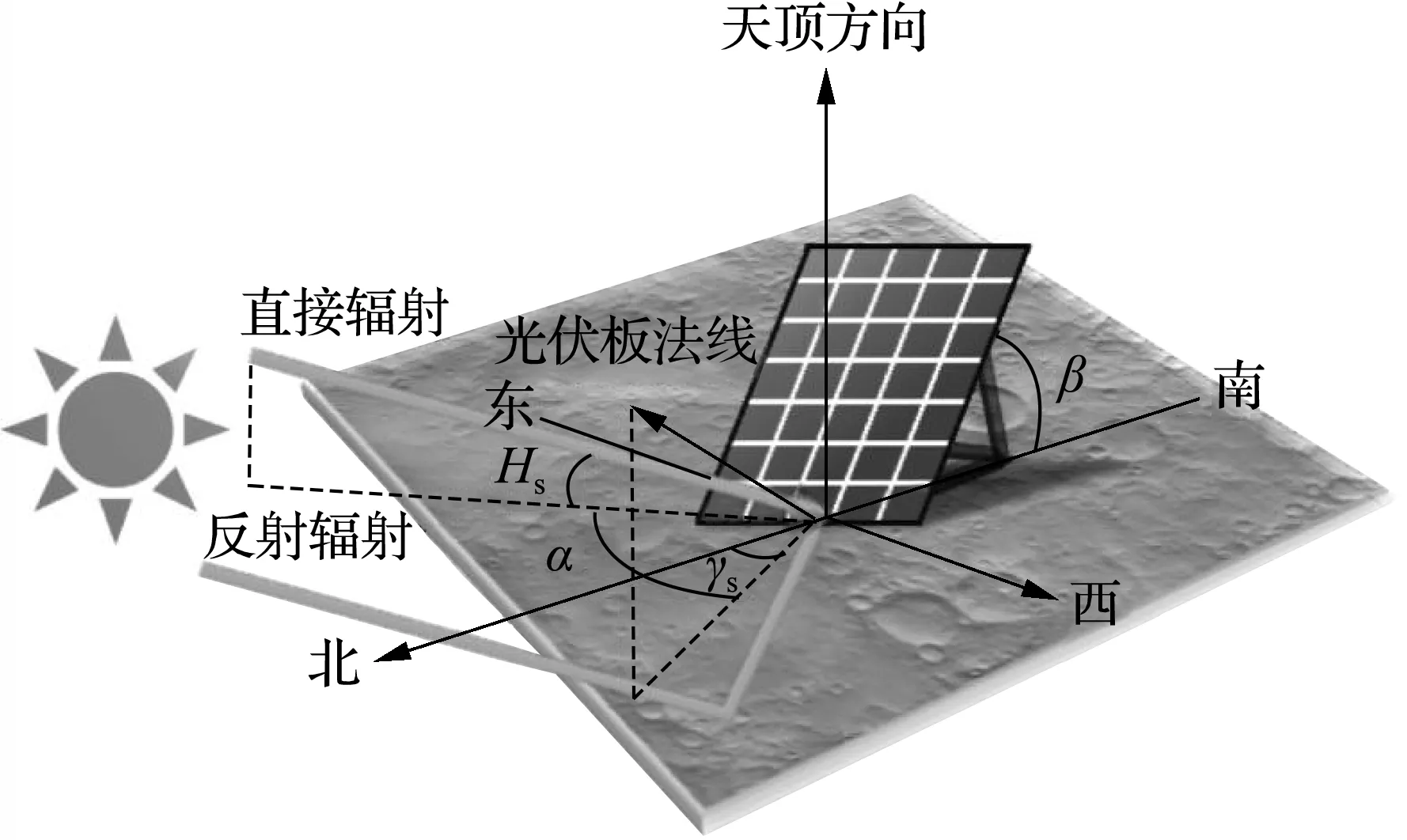
图4 倾斜面的太阳入射辐射示意图

式中，Iv为太阳辐射天顶分量，W/m2;Ih为太阳辐射水平分量，W/m2，由下式计算：

(12)

月面反射太阳辐射量IR按下式计算：

(13)

1.3 光伏板温度、效率以及阴影区月面温度计算

光伏板温度采用能量平衡法计算.使光伏板温度升高的能量为其吸收的未参与光电转换能量，主要包括3部分，如图1(b)所示：①光伏板S2正面吸收的未参与光电转换的太阳辐射；②光伏板S2正面吸收的太阳照射下月面S1发射的红外辐射；③光伏板S2背面吸收的位于阴影中月面S3发射的红外辐射.

光伏板发电量可通过太阳入射辐射量IT与光伏效率ηreal计算[23，40]；光伏板吸收的月面红外辐射量通过光伏板S2与太阳照射下月面S1、阴影中月面S3的辐射换热模型求解.

典型光伏板封装方式为正面采用减反射层，背面采用红外发射层.一般，光伏板正面减反射层的红外吸收率与发射率αs_front=εs_front=0.9[41]，可见光反射率γ=0.05[42-44]，背面红外发射层的红外吸收率与发射率αs_back=εs_back=0.9[45-46]，则光伏板吸收的未参与光电转换的能量Qin与自身发射的热辐射能量Qout为

Qin=IS+IG

(14)

(15)

式中，IS为光伏板吸收的未参与光电转换的太阳辐射能量；IG为光伏板吸收的红外辐射能量，包括太阳照射下月面S1的红外辐射能量IG_front与阴影中月面S3的红外辐射能量IG_back.各项可按以下方式计算：

IG=IG_front+IG_back

(16)

IS=(1-ηreal)(1-γ)IT

(17)

(18)

值得注意的是，由于光伏板的遮挡，光伏板背部的月面处于阴影之中，故光伏板背部所对月面的外部热源仅为光伏板，因此根据月面稳态温度计算方法建立阴影中月面S3温度TG_back的计算公式：

(19)

式中，XPV2G为光伏板S2背面对阴影中月面S3的辐射角系数，有

(20)

根据角系数的相对性可得到阴影中月面S3对光伏板S2背面的辐射角系数XG2PV，则有

(21)

参考多结光伏板的最新研究[6-7,47]，取光伏板在标准测试温度Tst=298 K下标定效率ηst=30%.多结光伏板温度衰减系数一般为βT=0.004～0.006 ℃-1[48-50]，由此可以计算光伏板经过温度衰减系数修正的实际效率ηreal为

ηreal=ηst[1-βT(Tcell-Tst)]

(22)

最终根据能量平衡Qin=Qout求解Tcell、TG_back、ηreal.

1.4 光伏板最优倾斜角度与朝向优化设计

1.4.1 输入特性导向型算法

未耦合温度衰减效应的倾斜角度和朝向以光伏板最大程度接收太阳入射辐射为目标，即输入特性导向型，则有

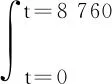
(23)

Einput=Iinputηreal

(24)

式中，βinput、γs_input分别为输入特性导向型算法求取的倾斜角度与朝向角；Iinput与Einput为该倾斜角度与朝向角所对应的整年太阳入射辐射量与单位面积可输出电能.

1.4.2 输出特性导向型算法

耦合温度衰减效应的倾斜角度和朝向以光伏板最大程度地输出电能为目标，即输出特性导向型，有

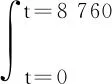
(25)

式中，βopt和γs_opt分别为输出特性导向型优化算法求取的最优倾斜角度和朝向角.

对比2种计算方法，单位面积可输出电能的相对改变量为优化率η，即

(26)

根据上述设计方法，本文以2020年为例，结合现今月球探索的热点区域(见表1)，沿月面0°经线近似选取南纬10°、40°、85°、90°四个坐标计算了月面不同纬度太阳高度角及月面温度，确定了光伏板最优倾斜角度与朝向，获得采用输出特性导向型优化算法的优化率与光伏板单位面积最大可输出电能的纬度分布规律.

表1 月面探索热点区域纬度位置及其研究特点

2 结果与讨论

2.1 不同纬度太阳高度角以及月面温度

南纬10°、40°、85°、90°的太阳高度角计算结果如图5(a)所示，太阳高度角整体呈现随纬度升高而减小的趋势.以南纬10°为例的月球低纬度地区，太阳高度角最大达81.44°；而在中纬度区域如南纬40°，最大太阳高度角降低至51.44°；当纬度达到85°时，最大太阳高度角仅为6.44°；纬度继续升高至极点时(90°)，昼夜交替逐渐转变为极昼极夜，出现接近4 200 h的连续光照区，然而极地1.59°的最大太阳高度角给当地太阳能利用带来了困难.

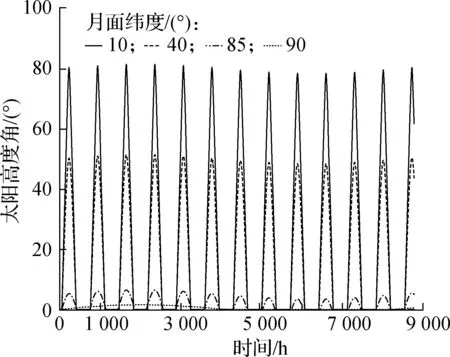
(a) 太阳高度角

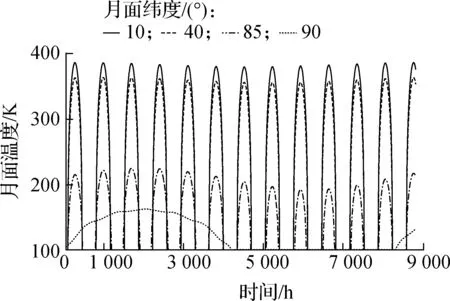
(b) 月面温度

根据式(8)，月面稳态温度变化趋势与太阳高度角变化趋势一致，如图5(b)所示，整体呈现出低纬度月面温度高、高纬度月面温度低的分布特点.以南纬10°与南极点为例，南纬10°的最高日间温度为386.18 K，而南极点的最高温度仅有163.39 K，二者差异可达222.79 K.

2.2 不同纬度光伏板最优倾斜角度以及朝向

对于最优朝向，与地球上的情况相同，位于南半球的光伏板朝向总是面向赤道(朝向正北)最佳，如图6中4条虚线均重合于90°的朝向角度.最优倾斜角度的纬度分布特点如图6中实线所示，采用输入特性导向型算法得到最优倾斜角度基本等于当地纬度，与地球上的情况一致；而采用输出特性导向型优化算法后最优倾斜角度整体增大，这主要取决于光伏板温度的作用.值得注意的是，纬度越低，优化算法对应的倾斜角度增量越大，究其原因，以温度衰减系数0.004 ℃-1为例，低纬度(5°)下的输入特性与输出特性各自峰值所对应的倾斜角度差异显著大于高纬度(85°)下，因此纬度越低对应的倾斜角增量越大，如图7所示；从不同温度衰减系数来看，根据式(22)，光伏板温度衰减系数越高，其发电效率受温度影响越大，则需要通过更大的倾斜角度来抵消.特别地，由上文计算得到2020年太阳直射点的纬度变化范围为-1.589°～1.572°，类比于地球赤道地区，在此纬度范围内无论采用何种算法，光伏板都宜水平放置，无需考虑倾斜角度与朝向[23,40].

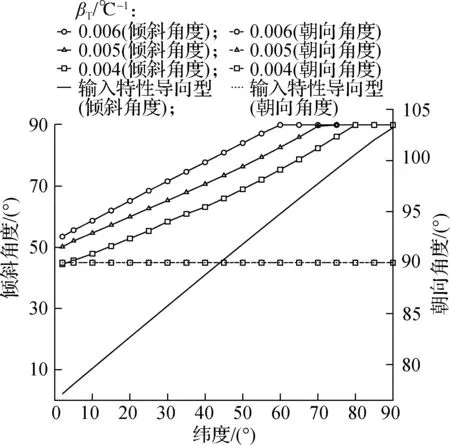
图6 光伏板最优倾斜角度及朝向角度对比

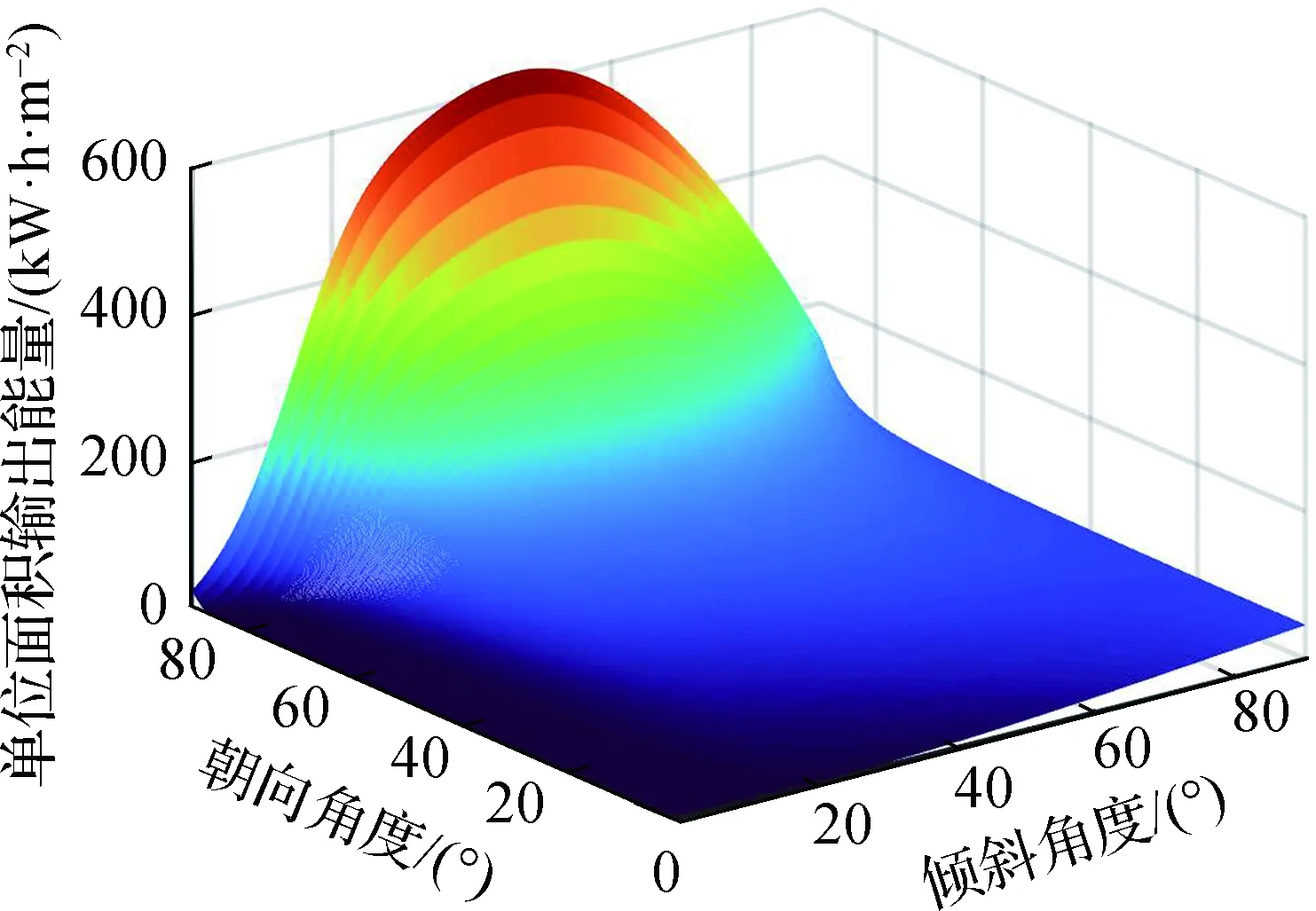
(b) 月面纬度5°光伏板输出特性

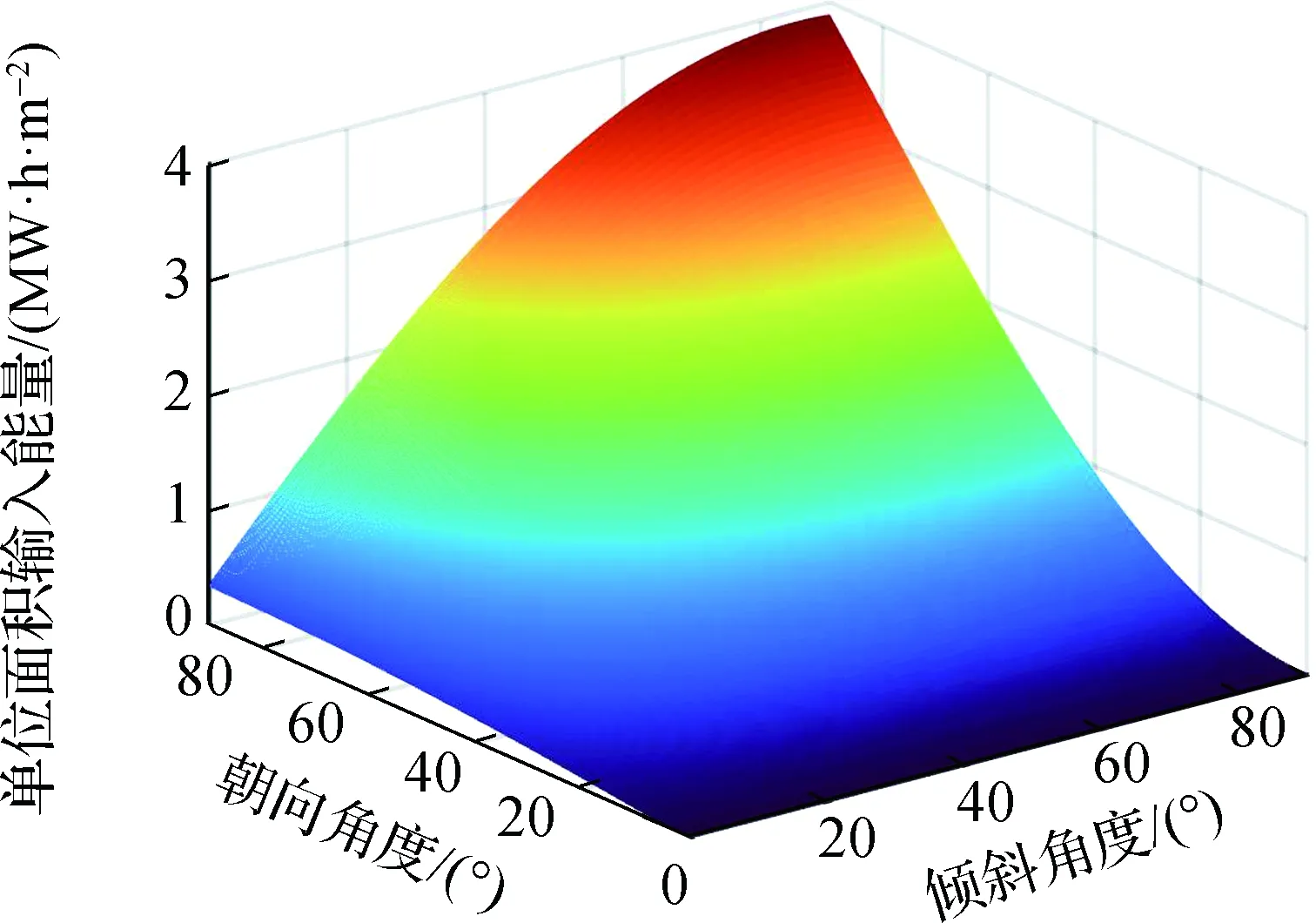
(c) 月面纬度85°光伏板输入特性

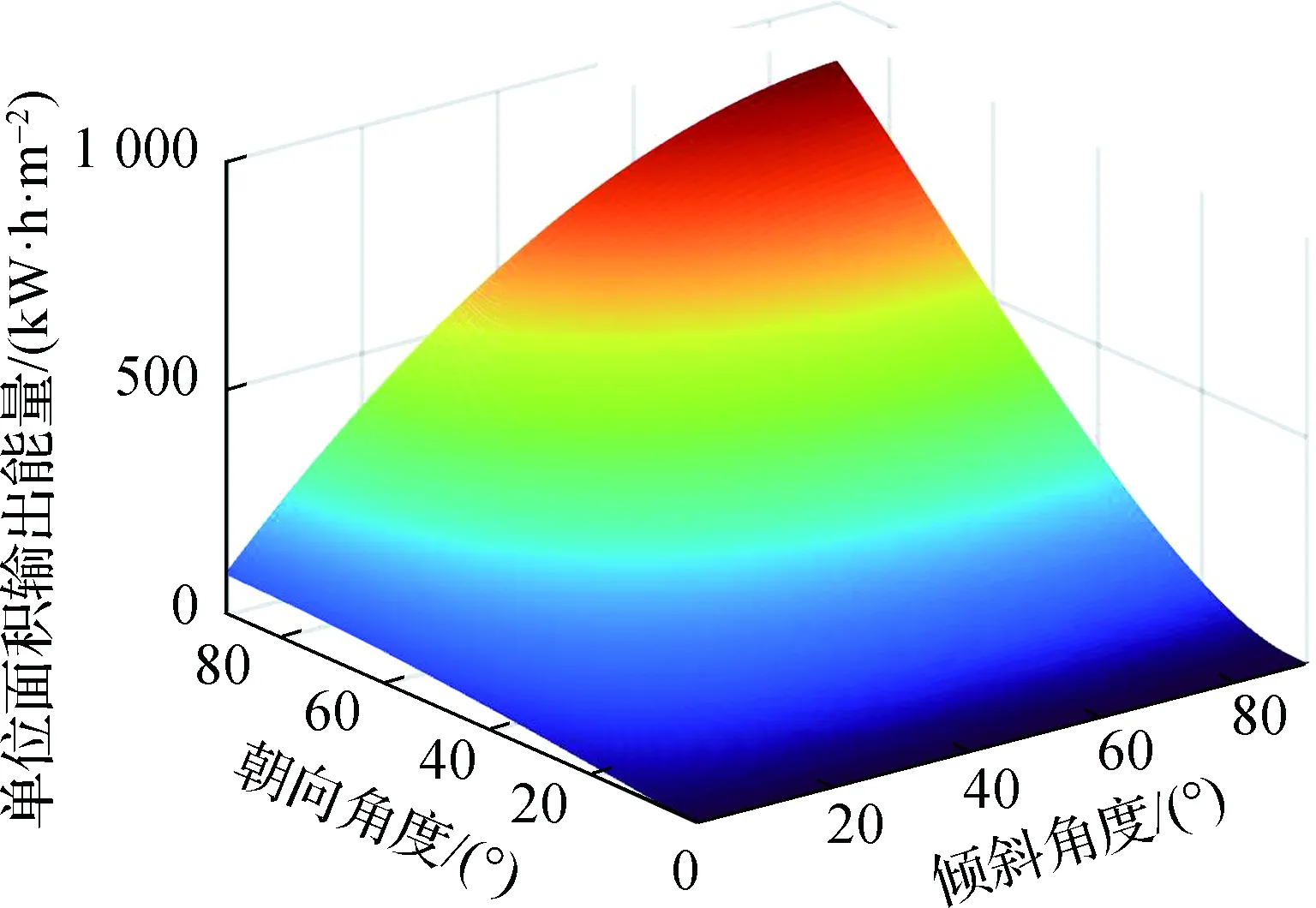
(d) 月面纬度85°光伏板输出特性

2.3 不同纬度光伏板温度及其影响因素

图8(a)为2种算法所对应的光伏板日间平均温度的纬度分布.采用输入特性导向型算法的光伏板在低纬度的日间平均温度甚至超过550 K；在采用输出特性导向型优化算法后，3种温度衰减系数的光伏板日间平均温度整体不超过355 K，实现了223 K的最高温降与50 K的平均温降，呈现出低纬度优化温降大、随着纬度升高优化温降逐渐减小的分布特点.其次，不同温度衰减系数下的光伏板日间平均温度差异小，最大仅为16.8 K.

进一步分析，以温度衰减系数0.004 ℃-1为例，如图8(b)所示，在一个月球日间(约350 h)，位于低纬度(10°)的光伏板在采用输出特性导向型优化算法求取的倾斜角度后，有效地将光伏板温度控制在409 K以下，相比于采用输入特性导向型算法最大实现了141 K温降，显著抑制了光伏板的过热；然而，在高纬度区域(85°)，如图8(c)所示，2种算法得到的光伏板温度均低于400 K，且两者几乎趋于相同.分析其原因，当纬度较低(10°)时，采用输入特性导向型算法得到光伏板倾斜角度仅为10.4°，此时光伏板S2背面与阴影中月面S3间的辐射换热角系数较大，二者温度呈现强相互作用，即阴影中月面S3的温度成为影响光伏板温度的主要因素，其528 K的高温显然不利于光伏板散热.而通过输出特性导向型算法优化后，光伏板倾斜角度增加至45.7°，一方面减弱了光伏板与阴影中月面S3之间的相互作用，另一方面减少了光伏板吸收的未参与光电转换的太阳辐射能量，其综合效益实现了较高的温降；当纬度较高(85°)时，光伏板倾斜角度接近于垂直，因而光伏板与月面辐射换热角系数小，光伏板温度与月面温度呈现弱相互作用，此时太阳入射辐射量成为影响光伏板温度的主要因素，因此2种算法差异微小.

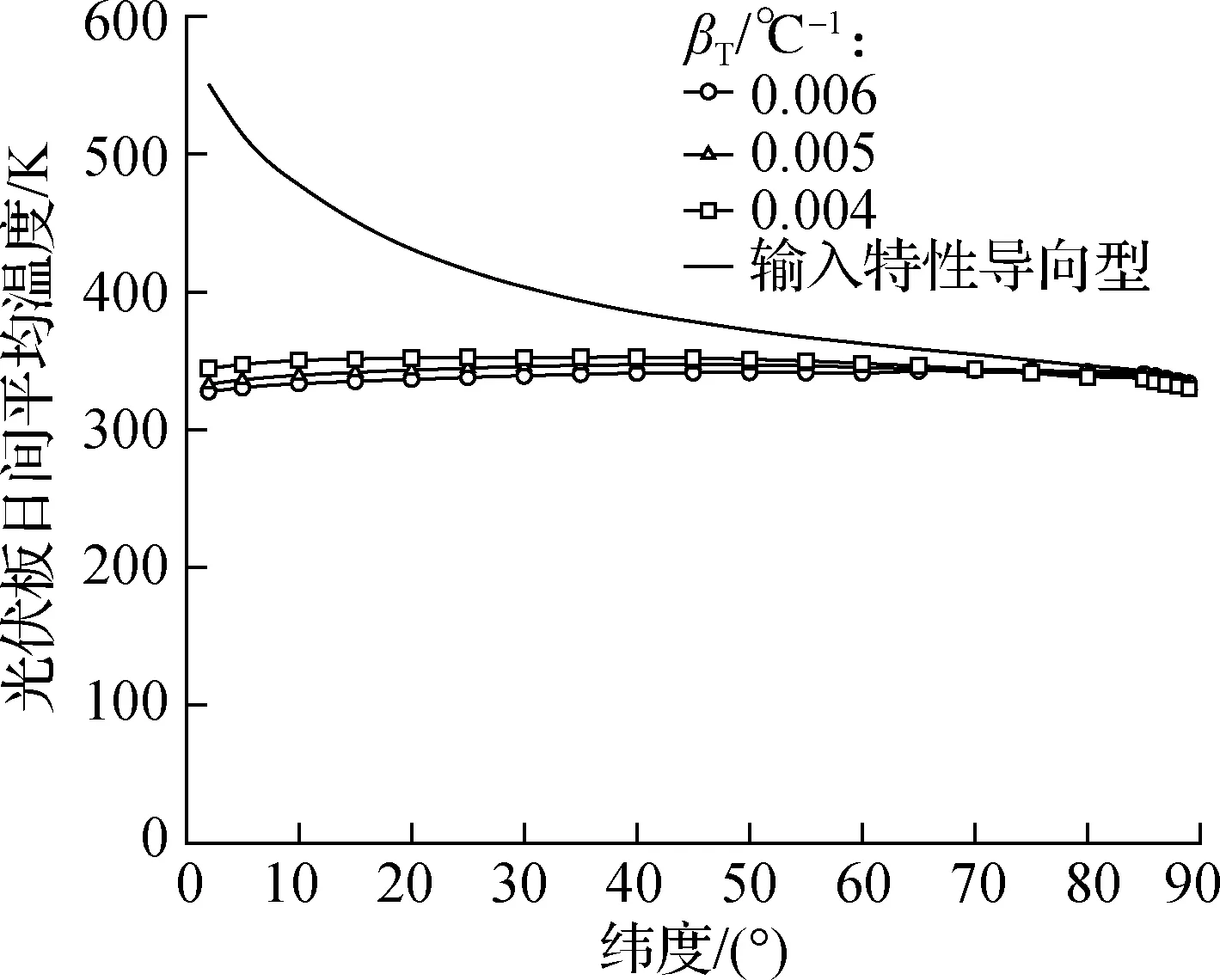
(a) 光伏板日间平均温度对比

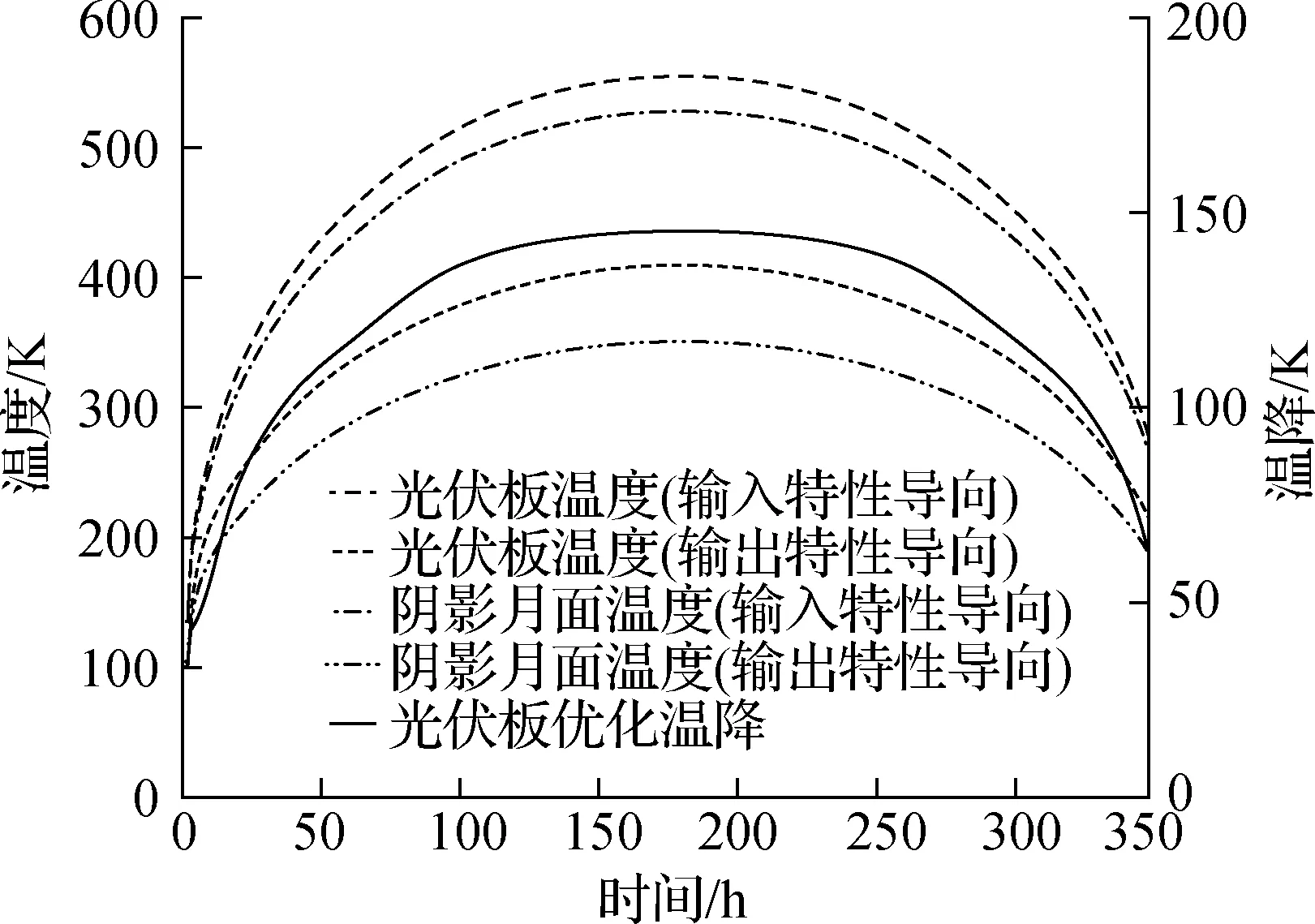
(b) 南纬10°光伏板温度、阴影月面温度对比

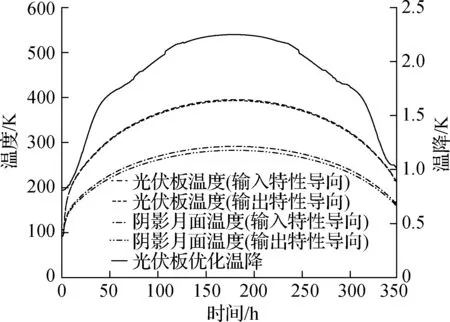
(c) 南纬85°光伏板温度、阴影月面温度对比

2.4 不同纬度下优化算法增益及单位面积最大可输出电能

采用输出特性导向型优化算法后的增益如图9中实线所示.从不同纬度来看，在3种温度衰减系数下均表现出低纬度优化效益显著、随着纬度升高优化效益减弱、80°以上甚至不足5%的特点.根据上文分析，这取决于光伏板温度的纬度分布特点；从不同温度衰减系数来看，整体呈现出温度衰减系数越高，优化算法效益越明显的特点.温度衰减系数0.004℃-1下平均优化率为63.51%，最高达到了634%，而温度衰减系数0.006℃-1下平均优化率为211.73%，低纬度下最大优化率超过1 800%，其原因与图6一致，高的温度衰减系数产生较大的倾斜角度差异，易实现更佳的优化效果.

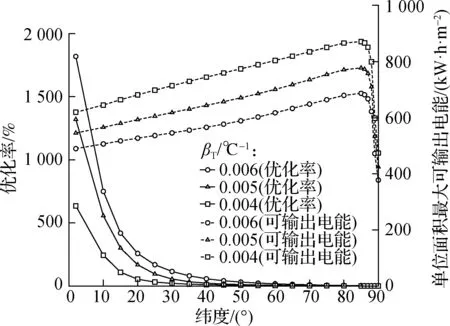
图9 优化率及单位面积最大可输出电能的纬度分布

在采用优化算法后，各纬度的2020年全年单位面积最大可输出电能如图9中虚线所示，纬度分布规律整体表现出低纬度单位面积最大可输出电能低、随着纬度升高呈现上升趋势、但在极点附近急剧下降的特点.当温度衰减系数为0.004 ℃-1，在低纬度5°时单位面积最大可输出电能仅约600 kW·h/m2，纬度升高至85°左右可达到870 kW·h/m2，但是在纬度88°附近从870 kW·h/m2下跌至474 kW·h/m2.其原因在于低纬度月面温度较高，光伏板需要较大的倾斜角度来控制热通量，这导致了光伏板的太阳入射辐射量减小，故转化为电能的部分也相应减少，即便采用优化算法后有良好的效果，但仍然无法抵消高温月面带来的负面影响，由此单位面积最大可输出电能随着纬度升高呈现上升趋势.而在纬度88°以上月面进入了连续光照区域，如图5(a)所示，此时极昼时间约4 200 h，对于一个月球日间(约350 h)来看太阳方位角变化十分微小，而根据式(12)，若太阳辐射的水平分量与光伏板法平面在水平面上投影的夹角α较大时，太阳入射辐射量较小，由此导致了单位面积最大可输出电能在极点附近急剧下降的纬度分布特点；从不同温度衰减系数来看，根据式(22)，温度衰减系数越小光伏效率整体越高，则单位面积最大可输出电能越高，与图9一致.

3 结论

1) 通过VSOP、ELP、天平动理论建立完整的月球轨道模型，计算了精确的太阳直射点、月面太阳辐射强度，并得到了月面任意位置在2020年的太阳高度角、方位角，由此计算各纬度月面温度，得到不同纬度下月面日间温差最大可达222.79 K.

2)针对不同纬度的巨大月面日间温差，提出耦合温度衰减效应的输出特性导向型倾斜角度优化算法.通过增大倾斜角度使光伏板日间平均温度控制在355 K以下，在低纬度区域实现了223 K的最高温降与50 K的平均温降，整体呈现出低纬度优化温降较大并随纬度升高优化温降减小的分布特点.

3) 采用优化算法后，3种温度衰减系数光伏电池的单位面积最大可输出电能均表现出低纬度较低、随着纬度升高呈现上升趋势、但在极点附近急剧下降、并在85°左右取到最大值的分布特点.与常规的输入特性导向型算法相比，在低纬度优化效益显著，最高可达1 800%，并随着纬度升高优化效益减弱.

4) 该方法以月球特殊的热环境为基础，建立了太阳、光伏板与月面的辐射换热模型，综合考量了月面温度、太阳辐射对光伏板温度的影响而实现光伏板倾斜角度的优化设计，对于高效利用月面太阳能资源具有指导性意义.