火焰特征量对快速烤燃的影响

肖 游，智小琦，王 琦，于永利，范兴华

（1. 中北大学机电工程学院, 山西 太原 030051；2. 吉林江机特种工业有限公司, 吉林 吉林 132021；3. 晋西工业集团, 山西 太原 030051）

目前，模拟快速烤燃常用的方法有3 种：一是热通量边界法[1-2]，即把燃料燃烧产生的热通量直接施加在烤燃弹外边界；二是温度边界法[3-6]，即将快速烤燃测得的温度直接作为烤燃弹外边界条件；三是热质量流法[7]，即将油池中燃料燃烧产生的高温混合物视为热质量流，作为快速烤燃计算域的入口边界条件。热通量边界法和温度边界法将均匀的热量加载在整个边界面上，虽然可以在一定程度上反映烤燃弹在快速烤燃条件下的响应特性，但是与实际火焰不一致，因为火焰强度是随时间变化的，不可能是恒定值，而且在实际的快速烤燃条件下，烤燃弹不同表面的火焰强度也是不同的；热质量流法虽然能较理想地模拟烤燃弹在火焰中的受热情况，但是实际火焰中物质粒子在截面的流动并非均一、恒定的，而是随位置不断地变化，因此与实际情况也不完全相同。

为使快速烤燃的数值模拟与实际火烤情况更加吻合，采用FDS 软件模拟油池火焰对烤燃弹不同位置的传热过程，并将其作为边界条件直接导入Fluent 进行数值模拟，这将是一种新的更有效的方法。本研究拟采用该方法在基于B 炸药（60%RDX/40%TNT）快速烤燃试验的基础上进行数值模拟，研究火焰特征量对B 炸药快速烤燃特性的影响及规律，以期为快速烤燃数值模拟方法提供新的技术途径，也为快速烤燃试验设计提供借鉴。

1 理论模型

1.1 池火燃烧模型

Rehm 等[8]提出的流体力学简化方程被许多池火研究者采用，称为“低马赫数”燃烧方程，该方程描述了化学能释放和浮力驱动气体低速运动特征。

“低马赫数”燃烧方程通过流体动力学、热传导和燃烧的基本守恒方程计算火焰，采用低马赫数大涡模拟（large eddy simulation）描述气体燃料和燃烧产物与火焰周围局部大气的湍流混合，基本思想是当涡流足够大并占据混合物的大部分时，可用流体动力学方程计算，而小尺度涡流运动则可以予以简化或忽略。其通用方程组如下

1.2 绝热表面温度

根据Wickström[12]的研究，用平板温度计测量火灾中物体的表面温度，该温度接近绝热表面温度，以绝热表面温度作为计算火灾作用下物体温度变化的边界条件，并应用于数值模拟中。

1.3 炸药分解动力学

对B 炸药的数值模拟做如下假设：(1) 忽略炸药的体积变化；(2) 炸药的自热反应遵循Arrhenius 方程；(3) 忽略气体产物对传热的影响。

炸药在烤燃过程中的质量、动量、能量的连续方程可用以下通用形式表示[13]

表1 炸药和壳体的物性参数Table 1 Physical parameters of explosives and shell

表2 炸药反应动力学参数Table 2 Reaction kinetic parameters of explosives

2 B 炸药快速烤燃试验与数值模拟研究

2.1 B 炸药快速烤燃试验

火烧装置由油池、支架、航空煤油、热电偶、数据采集系统、烤燃弹组成。烤燃弹壳体尺寸为∅130 mm×430 mm，壳体和端盖的厚度均为15 mm，长径比为3.31。B 炸药（60%RDX/40%TNT）药柱尺寸为 ∅100 mm×400 mm，装药充满空间，装药量为5 309 g。油池的尺寸为1 500 mm×1 200 mm×100 mm，油池与支架材料均为45 钢。火焰源为JP-8 航空煤油。采用K 型热电偶测温，精度为0.1 K。如图1 所示，烤燃弹水平放置，在烤燃弹周围（烤燃弹中心径向左侧下部、左侧上部和右侧下部距烤燃弹表面10 cm 的位置）设置3 个火焰温度监测点，使用FLUKE 多通路测温仪（测量精度0.01 K）测量火焰温度。采用起爆器击发电点火头点燃航空煤油。

图1 快速烤燃试验现场布置Fig. 1 Layout of the fast cook-off test

快速烤燃过程中各监测点的温度-时间变化曲线如图2 所示。点火后16.0 s 内温度达到550 ℃，其中测点2 在烤燃过程中发生断路，未测出数据。测点1 和测点3 的火焰达到稳定阶段的平均温度分别为832 和862 ℃。点火后63.4 s 烤燃弹发生响应，伴随一声巨响，各监测点断路。烤燃弹快速烤燃试验在野外进行，响应后现场全部毁坏，油池损坏，回收的部分破片残骸如图3 所示（由于试验在野外开展，场地复杂，破片未能完全回收）。考虑到破片较碎，现场破坏严重，因此判定响应等级为爆轰反应。

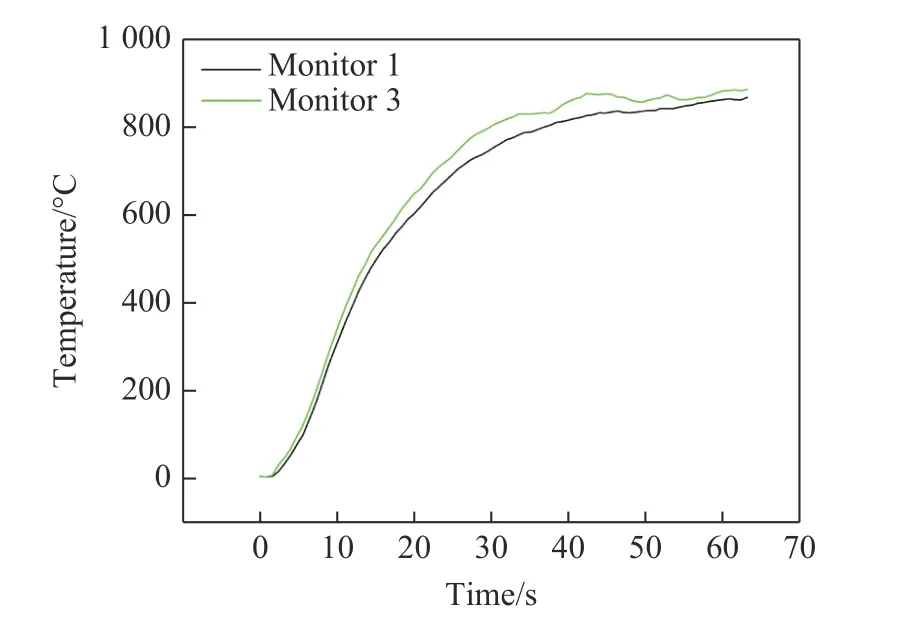
图2 温度-时间曲线Fig. 2 Temperature-time curves

图3 响应后烤燃弹的破片残骸Fig. 3 Fragment debris of the cook-off bomb after response

2.2 基于试验的数值模拟

采用FDS 软件计算航空煤油燃烧对烤燃弹的传热，建立快速烤燃模型，模型包含油池、燃料和烤燃弹，如图4 所示。由于实际火烧试验在开放空间中进行，因此将计算域的壁面和顶部设置为open 类型，将烤燃弹表面设置为绝热表面，忽略烤燃弹支架对传热的影响。

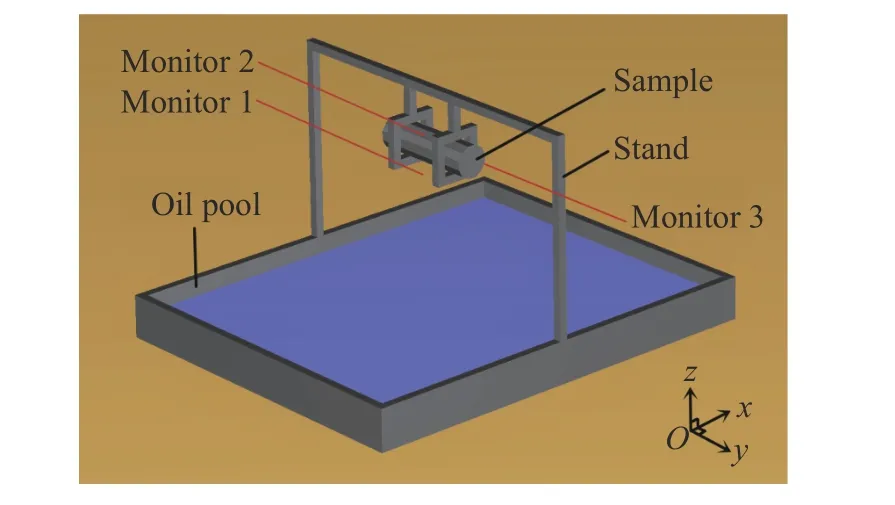
图4 快速烤燃模型Fig. 4 Model of the fast cook-off

航空煤油的成分十分复杂，包含221 种组分[18]，对于不同的燃烧进程和火焰位置，其产物也有所不同，目前难以实现如此复杂的混合物的模拟计算。为此，采用与航空煤油的关键物理及化学特性相近的替代燃料进行模拟。Violi 等[19]和Cathonnet 等[20]用JP-8 航空煤油中的主要成分C12H26作为替代燃料，其沸点、反应产物等与JP-8 基本一致。在本研究的FDS 模型中也采用C12H26替代JP-8 航空煤油，JP-8 燃料参数如表3 所示，其中： ΔH为燃烧热， α为 热辐射吸收系数，Q˙为单位面积热释放率。

表3 JP-8 燃料的燃烧参数Table 3 Combustion parameters of JP-8 fuel

由于采用大涡模拟方法进行火灾模拟，且只考虑湍流场中的大尺度涡流，简化或忽略小尺度涡流，因此，网格尺寸会影响计算结果的精确度，对于池火模拟，只有使用亚网格尺度的网格计算才能达到精度要求。为此，采用尺寸为0.3 m×0.3 m×1.0 m 的计算域进行最优网格尺寸验证，并根据不同尺寸网格火焰模拟中同一位置的温度拟合得到计算精度。计算精度及计算时间与网格尺寸的关系见图5 和图6。

图5 计算时间与网格尺寸的关系Fig. 5 Relation between calculation time and mesh size

图6 计算精度与网格尺寸的关系Fig. 6 Relation between accuracy and mesh size

由图5 和图6 可知：网格尺寸在0.05～0.20 m 之间时，计算时间的差距不大，但计算精度随网格尺寸的减小迅速增加；网格尺寸在0.01～0.05 m 之间时，随着网格尺寸的减小，计算时间呈指数增加，而计算精度的变化趋势减缓。综合考虑计算精度和计算时间，采用的计算域尺寸为5.0 m×5.0 m×4.0 m，网格尺寸为0.02 m×0.02 m×0.02 m。

在FDS 中采用集总组分法对燃料、空气、燃烧产物和烟气进行定义，空气中的氧气和氮气为反应物，燃烧产物由水、二氧化碳和氮气组成，烟气的生成量取燃料的6%[21]。设置油料的点火点，当火焰将烤燃弹完全包裹时，快速烤燃的模拟场景如图7 所示。

图7 池火快速烤燃模拟场景Fig. 7 Simulated scene of the fast cook-off in pool fire

在与快速烤燃试验中测点1 和测点3 相同位置处设置2 个温度监测点，通过池火数值计算，得到烤燃弹周围火焰温度随时间变化曲线，如图8 所示。点火18.6 s 后，温度升至550 ℃，测点1 和测点3的平均温度分别为842 和845 ℃，相对偏差分别为2.7%和1.3%，数值模拟结果与试验结果非常吻合。

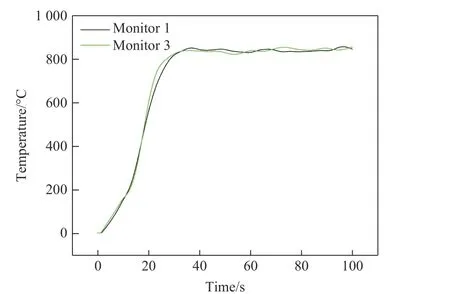
图8 火焰中测点温度随时间变化曲线Fig. 8 Temperature-time curves of gauging points in flame

放置烤燃弹的池火火焰温度和辐射热通量的截面云图如图9 所示。火焰将烤燃弹完全包裹，烤燃弹侧表面四周的火焰温度保持均匀，火焰温度峰值出现在烤燃弹下方。辐射热通量峰值位置与温度峰值位置几乎相同。但是烤燃弹两个端面的火焰结构稀薄，温度也较侧表面温度低。这与烤燃弹放置方向有关，试验时没有将烤燃弹的轴向与油池长边平行。由此可见，试验时烤燃弹的放置位置和方向是影响烤燃弹四周火焰温度的重要因素。

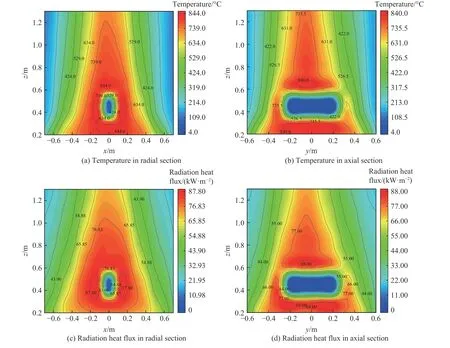
图9 烤燃弹中心截面温度和辐射热通量Fig. 9 Temperature and radiation heat flux of the central cross-section of cook-off bomb

对比实际烤燃试验，可以看出，烤燃弹的不同位置吸收的热量有所不同。在模型中将烤燃弹分为6 个部分（将烤燃弹侧表面等分为4 个部分，最靠近池底编号为1，2～4 顺时针排列，5 和6 对应左右两个端面），如图10 所示。同时监测烤燃弹6 个位置的绝热表面温度变化，结果如图11 所示。比较不同位置处的温度曲线，将点火后的火焰变化分为3 个阶段：点火阶段、发展阶段和稳定阶段。在点火阶段，火苗由点火点迅速蔓延至整个油面并逐渐上升，在火焰的作用下烤燃弹下部温度首先升高，随后烤燃弹侧壁和端面温度上升，而烤燃弹上表面温度几乎为常温。在发展阶段，火焰开始波动，液体燃料蒸发，燃烧速率加快，火焰逐渐将烤燃弹包裹其中，此时烤燃弹侧表面温度迅速增加。由于烤燃弹端面与气流流动方向平行，吸收的热量不稳定，且烤燃弹轴向与池宽度方向平行，两端火焰结构较稀薄，因此温度波动较大，而上表面温度较稳定地持续上升。在稳定阶段，火焰将烤燃弹完全包裹，火焰的变化仅为自身的非周期性脉动，各表面温度趋于动态稳定，但烤燃弹的上测点温度较下测点温度低。这主要是由于烤燃弹放置位置距离油面较高所致。

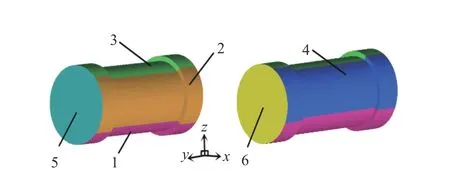
图10 烤燃弹模型与测点示意图Fig. 10 Schematic diagram of the cook-off bomb model and gauging points

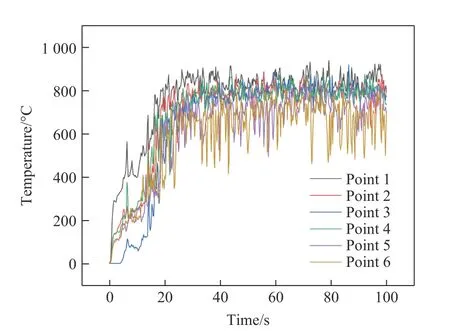
图11 壳体不同位置的温度随时间变化曲线Fig. 11 Temperature-time curves at different positions of shell

如图12 所示，在药柱的不同方向设置温度监测点，分析药柱从几何中心到不同表面的温度变化情况。其中，3 个径向监测点的间距与轴向监测点的间距均为0.1 mm。图13 为径向和轴向监测点的温度-距离曲线。从图13 可以看出，由于B 炸药的熔化温度在81 ℃左右，a、b、c、d4 个方向的熔化层厚度分别为3.454、3.733、3.543、2.287 mm，由于熔化量极少，熔化部分几乎监测不到流动速度。药柱中a、b、c径向药柱表面温度分别为167.6、185.6、173.5 ℃，而药柱轴向端面温度为144.3 ℃。可见，药柱表面径向温度均高于端面温度，药柱下表面温度高于侧表面温度，而侧表面温度高于上表面温度。此外，药柱中a、b、c、d4 个方向分别距药柱表面13.70、14.13、14.00 和12.82 mm 处的炸药温度仍为初始温度，考虑到各方向的热量传递距离与药柱温度发生变化的深度相同，因此试件下表面的热量传递距离最大，其次是侧表面，接着是上表面，最后是端面。由此可见，火焰特征量的变化将会影响药柱内部传热，特征量越大，热量传递越深。

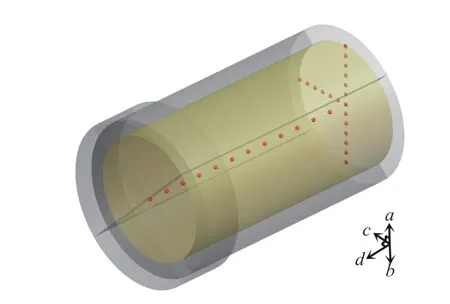
图12 测点设置示意图Fig. 12 Schematic diagram of gauging point setting

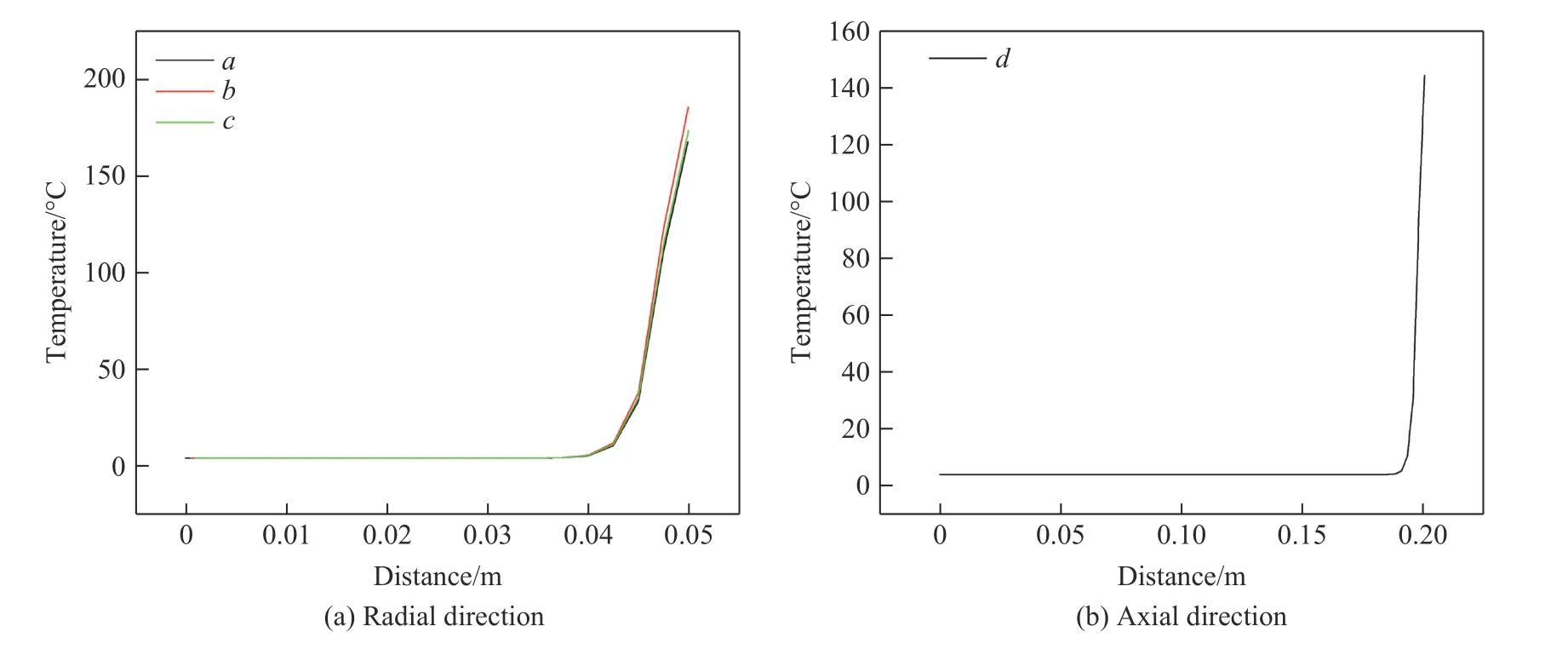
图13 药柱径向和轴向温度随距几何中心距离的变化曲线Fig. 13 Variations of temperature in radial and axial directions with distance to the geometric center of charge

3 火焰特征量对快速烤燃的影响

3.1 参数设置

影响烤燃弹四周火焰特征量的因素主要有燃料性质、油池尺寸及烤燃弹与油池的相对位置。在油料确定的条件下，主要影响因素是油池尺寸以及油池与烤燃弹的相对位置。为了研究火焰特征量的变化规律，在油池尺寸不变的条件下，首先将烤燃弹轴向平行于油池长边放置，其次调整烤燃弹底部距油面的高度（烤燃弹的放置高度），将烤燃弹的放置高度390 mm 调整为420、360 和330 mm。此外，针对试验所用的烤燃弹，设计了长宽比与试验相同的两种不同尺寸的油池，分别为2 100 mm×1 700 mm×130 mm 和3 000 mm×2 400 mm×130 mm，烤燃弹的放置高度均为390 mm，且烤燃弹轴向与油池长边平行，其余数值模拟参数均与2.2 节相同。

3.2 结果与讨论

表4 列出了油池尺寸为1 500 mm×1 200 mm×100 mm，烤燃弹轴向与油池长边平行时，改变烤燃弹放置高度后数值模拟得到的表面温度结果。

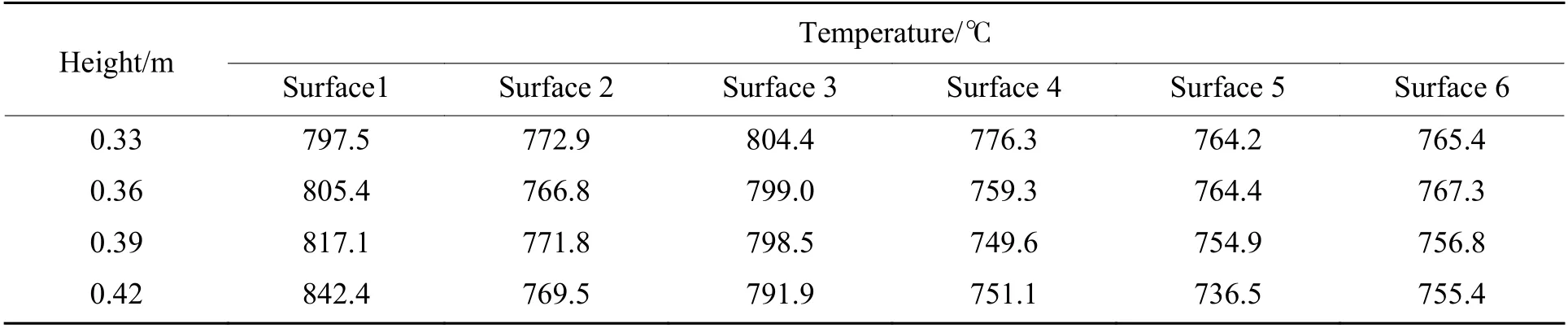
表4 烤燃弹放置高度不同时各表面的温度Table 4 Temperatures of each surfaces at different heights of the cook-off bomb

从表4 可以看出，随着烤燃弹放置高度的增加，烤燃弹表面温度发生变化。烤燃弹底面（Surface 1）温度随放置高度的增加而升高；上表面（Surface 3）温度随放置高度的增加而降低，但变化幅度不大；左端面（Surface 5）和右端面（Surface 6）温度随放置高度的增加在小范围内波动，当放置高度增大到390 mm 后，两端面温度稍有降低。由此可见，在本研究的工况下，烤燃弹的放置高度主要影响烤燃弹上下表面的温度，对侧面（Surface 2 和Surface 4）和端面温度的影响较小。从另一个角度看，当油池的尺寸合理，烤燃弹的放置高度可以在一定的范围内变化，此时其四周温度的变化幅值较小。

如图14 所示，当放置高度从0.33 m 增加到0.36 m 时，烤燃弹各表面温度变化较小，随着放置高度继续增加，各表面温度的变化增大。当烤燃弹的放置高度为0.33 m 时，烤燃弹各表面之间的最大温差为40.2 ℃；当放置高度继续增加，表面的最大温差增大；当放置高度为0.42 m 时，最大温差达到105.9 ℃。由此可见，烤燃弹表面温度的均匀性受烤燃弹放置高度的影响较大，烤燃弹表面峰值温度由上表面转移到了下表面，且放置高度越高，烤燃弹表面温度差值越大。

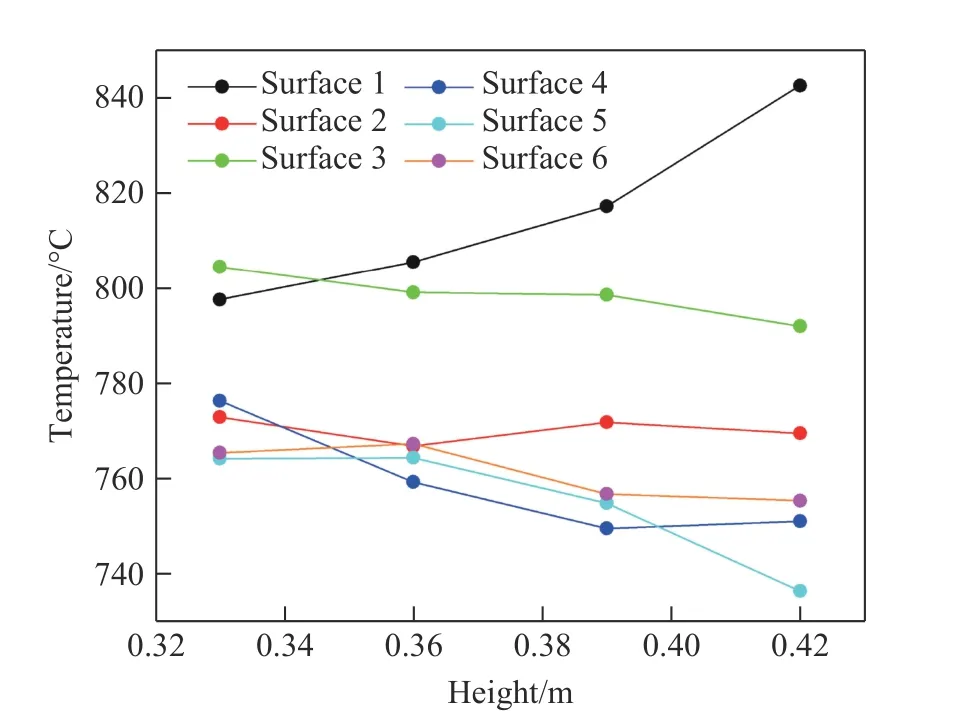
图14 烤燃弹放置高度不同时各表面温度变化曲线Fig. 14 Variations of each surface temperature with different heights of the cook-off bomb

影响烤燃弹表面温度的主要因素为火焰的热通量，各表面的热通量达到稳定后的平均值如表5所示。由表5 可知，随着烤燃弹放置高度的增加，烤燃弹下表面的热通量增加，上表面的热通量降低，其余表面的热通量均有略微降低的趋势。并且，随烤燃弹放置高度的增加，烤燃弹下表面的辐射热通量占比由94%提升至95%左右，上表面的辐射热通量占比维持在95%左右，其余表面的辐射热通量占比维持在92%左右。造成这种变化的原因是烤燃弹位于火焰中心，扰乱了涡流卷吸空气，影响了燃料的燃烧。当烤燃弹位置较低时，燃料并未发生完全燃烧，燃烧产物主要分布在烤燃弹上方，因此烤燃弹上表面的辐射热通量较高；随着烤燃弹位置的升高，燃料已充分燃烧，烟气流动带动燃烧产物冲击烤燃弹下表面，造成热通量峰值由烤燃弹上方转移到烤燃弹下方。

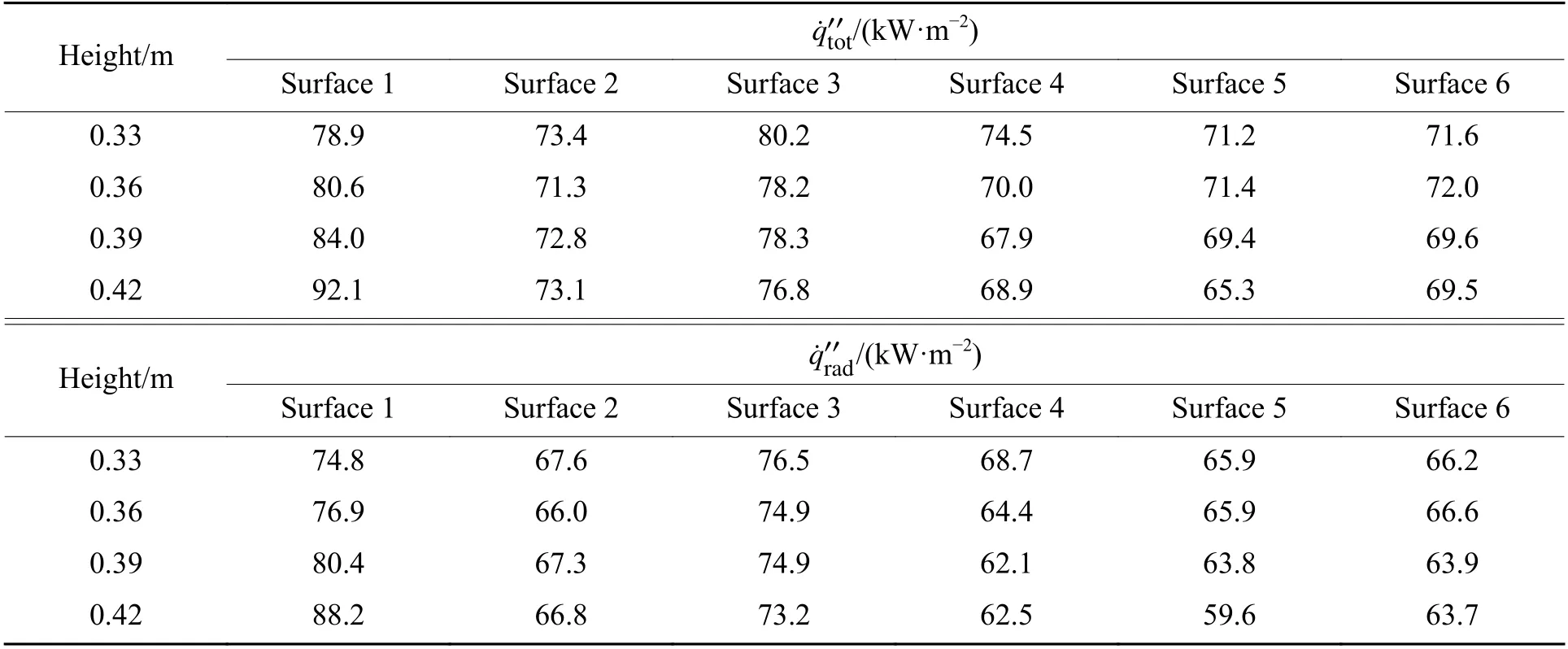
表5 烤燃弹放置高度不同时各表面的热通量Table 5 Heat flux of each surface of the cook-off bomb with different heights

表6 显示了不同油池尺寸工况下烤燃弹表面不同位置的平均温度。由表6 可见，当油池尺寸增加时，烤燃弹各表面温度均达到800 ℃以上，各表面温度的变化趋势如图15 所示。随着油池面积的增加，除两个端面的升温速率基本一致外，其余表面的升温速率不同。其中：烤燃弹底面温度随着油池面积的增加先升高后降低；当油池面积增加到3.57 m2时，上表面和端面温度受油池面积的影响较大，上表面升温64.4 ℃，两端面升温均超过95.0 ℃；当油池面积增加到7.20 m2时，上表面和端面的升温速率急剧降低。由此可见，烤燃弹表面温度并不会随着油池面积的增加而一直增大，当形成的火焰厚度足够大时，烤燃弹表面温度不再发生明显的变化。随着油池面积增加，烤燃弹表面的最大温度差无明显变化，均在64.0 ℃左右，说明在相同放置高度下，增加油池面积在一定程度上对火焰稳定性的影响较小。

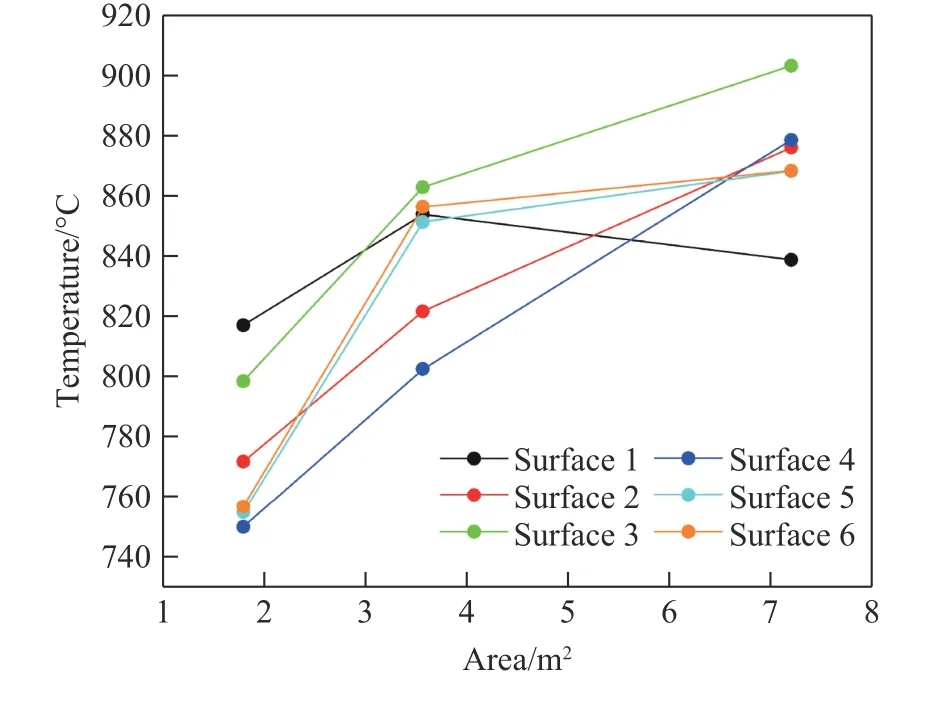
图15 烤燃弹各表面温度随油池面积的变化Fig. 15 Variations of surface temperature of the cook-off bomb with the area of oil pool

表6 油池尺寸不同时烤燃弹各表面温度Table 6 Each surface temperature of the bomb burned in the oil pool with different sizes

表7 显示了不同油池尺寸对应的烤燃弹各表面的热通量。由表7 可见， 随着油池尺寸的增加，除烤燃弹下表面的热通量先升高后降低外，其余表面的热通量均保持升高趋势。但是，对流热通量的绝对值随油池尺寸的变化基本不变。可见，火焰中蕴含的燃烧产物是发射辐射热通量的载体，随着火焰厚度的增加，燃烧产物增加，辐射热通量增大。

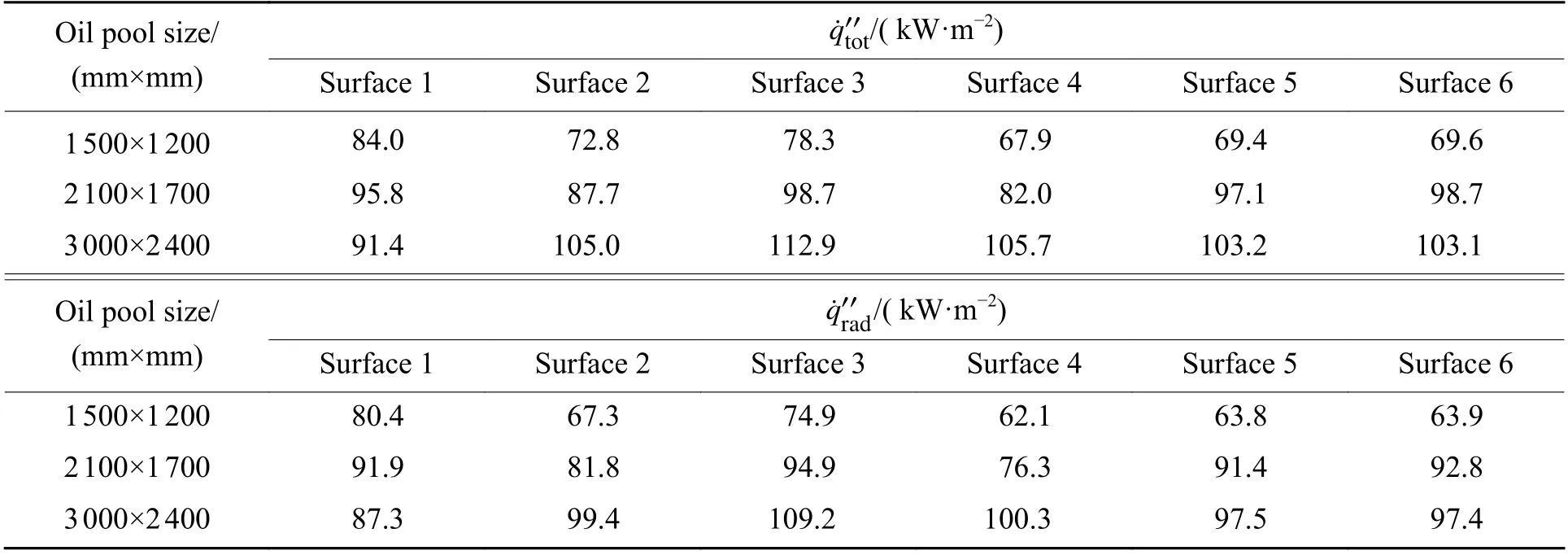
表7 油池尺寸不同时烤燃弹各表面热通量Table 7 Heat flux of each surface of the bomb burned in the oil pool with different sizes

此外，当油池面积增加至7.2 m2时，烤燃弹下表面的温度和辐射热通量均降低。由此可以看出，当油池面积较大时，烤燃弹下方容易出现燃料未完全燃烧的现象，从而导致温度和辐射热通量的变化。

综上所述，快速烤燃时，油池尺寸是影响烤燃弹温度的因素。烤燃弹表面温度的变化主要由辐射热通量主导，而释放辐射热通量的载体为火焰中的燃烧产物颗粒。燃料是否完全燃烧将影响烤燃弹快速烤燃试验结果。

4 结 论

为研究快速烤燃弹放置高度和油池尺寸对池火特征量的影响，采用FDS 软件建立池火模型，进行了快速烤燃的数值模拟，得到如下结论。

(1) 使用FDS 建立的池火燃烧模型能较准确地模拟快速烤燃下烤燃弹的加热情况，并通过Fluent 模拟烤燃弹内部的传热，更加精准地获取了火焰结构和烤燃弹周围的温度分布，为快速烤燃试验设计提供了指导。

(2) 火焰对烤燃弹各部位的不同影响源于火焰特征量的变化，火焰特征量的变化受烤燃弹放置位置和油池尺寸的影响，火焰中辐射热通量峰值由烤燃弹上方转移到烤燃弹下方。在一定条件下，烤燃弹放置位置越低，烤燃弹上表面温度越高，烤燃弹表面温度越均匀；增大油池尺寸时，辐射热通量的变化较明显，烤燃弹表面温度的变化由辐射热通量主导。