用于吊具位姿估计的改进SIFT立体匹配方法

王欣月，赵柏山

（沈阳工业大学信息科学与工程学院，沈阳 110870）

1 引言

在传统制造业现代化的今天，计算机视觉已经成为了当下人们探讨的焦点，计算机视觉技术应用于传统制造业将具有重要意义。物理传感器[1]、结构光[2]、激光[3]等技术，都已被用来测量目标物体的三维信息，在无人工干豫条件下达到了精准的效果。然而现有的方法采用的硬件设备都相对昂贵、不易安装，普及难度大。而机器视觉恰好能弥补这方面的缺陷。本研究将双目视觉技术与传统工业相结合，通过结合Harris算子和极限约束来改进立体匹配算法，以提高匹配的精度，利用得到3个特征点以及1个验证的坐标来求取吊具的位姿，在精准识别的同时节省人力资源。

2 方法概述

改进方法首先对采集的图像进行预处理，同时对双目相机进行标定，获取相机的内外参数，根据所得参数对图像的特征点提取；然后根据改进的SIFT算法进行立体匹配，得到精准的物体坐标；最后根据3D-2D的PnP求解吊具的位姿。

2.1 图像预处理与相机标定

为了更精准地得到物体的三维坐标，首先需要进行图像预处理操作。此处采用对灰度图像处理效果最好的加权平均值法对图像进行灰度处理，然后通过对比选择中值滤波法对图像进行滤波处理。

在Windows10系统下利用MATLAB R2019a环境，通过张氏标定法[4]进行双目相机标定。得到的左右相机内参为：

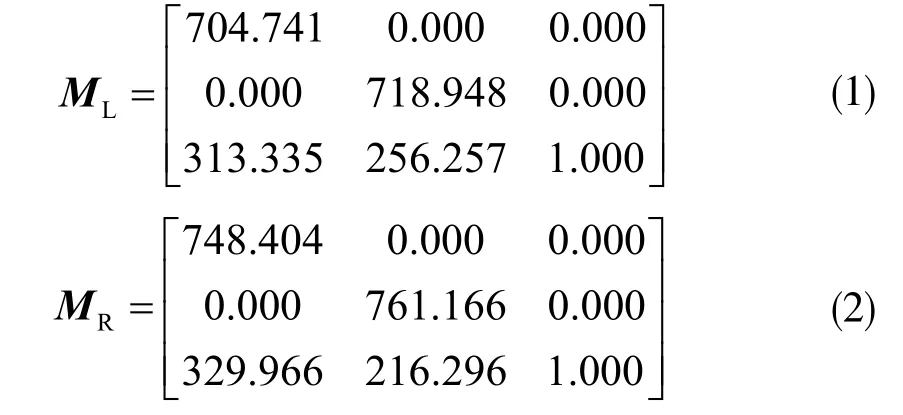
左右相机径向畸变参数为：

外参旋转矩阵为：

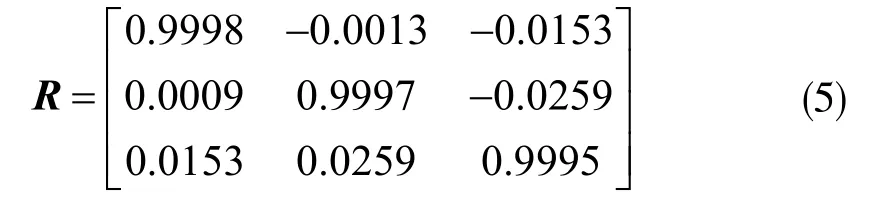
外参平移矩阵为：

2.2 立体匹配算法改进

SIFT算法是由David G.Lowe于2004年正式提出的一种基于局部特征的匹配算法。它主要包含尺度空间极值点检测、精确定位、特征点方向和特征描述子的产生等步骤。

由于传统的Harris角点提取方法不能很好地适应尺度变换，以及SIFT的特征描述子向量维数过高，造成图像的匹配不够快，在此提出一种基于SIFT的改进算法，把Harris算子、极限约束与SIFT算法有效地结合在一起。该方法在保留SIFT方法优点的同时，可以有效地降低特征点数和提高查找速度，使其达到更好的效果。改进方法的主要步骤如下：

步骤1：构建尺度空间的特征点

由于Harris检测算子对尺度的变化比较敏感，所以用该检测算子把SIFT算法中的极值点替换掉。改进的角点检测算子如下：

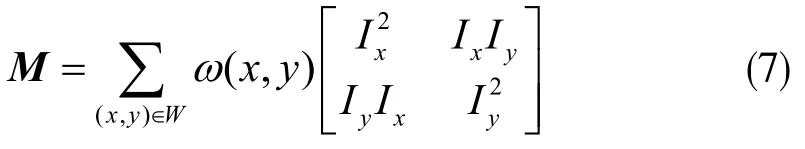
步骤2：图像的角点检测

计算亚像素特征点坐标，通过迭代优化，使误差最小，最终得到具有较高精度的角点坐标。

步骤3：引入极限约束

极限约束原理如图1所示。在右图中搜寻候选点。在立体匹配过程中，为了减少搜索时间、提高搜索精度，常常添加约束条件进行搜索。图中Ol和Or分别为两个相机投影的中心点；Ol和Or的连线交两平面于el和er，空间中点P与Ol、Or连线分别交于p和q，p与el连接的直线就是极限，因此p匹配点一定在er与q的连线上。

图1 极限约束原理

由此可以推导出，当相机所有参数均已知时，就可得到基础矩阵F。根据极限约束原理，计算左图特征点在右图上的极线，取极线上下10像素范围里的角点作右图像上的特征点。此方法把特征点的搜索由2维降到1维，有效提高了搜索的效率。

步骤4：确定关键点位置方向

通过与关键点相邻的像素点可以获取到关键像素点（x,y）梯度模值和方向：

对关键点3×3邻域窗口进行采样[5]，对相邻像素的梯度进行统计，用梯度柱状图来表示，然后选择最大幅度的两个方向，作为主方向和辅方向[6]，以此即可使关键点有旋转的不变性。

步骤5：SIFT关键点描述子的生成

SIFT算法可以将尺度不变与梯度向量结合起来，使其对目标物体尺度变换、旋转、模糊等方面表现出良好的稳定性，同时还具备一定的抗噪性和很好的鲁棒性，有效地识别出图像中的关键点。与其它算法相比，这是一个很好的局部特征描述子，然而同时此方法还需要产生128个维度的描述子，使得建立特征描述子和后续的匹配耗时较多，计算复杂。对此，可通过降低特征向量的维度来降低计算时间。对该特征点的描述方法如图2所示。取以关键点为中心的8×8的像素区域，每4×4的窗口内计算出8个方向直方图，由此，关键点被表示为4×8的32维特征描述子。

图2 由关键点邻域梯度信息生成特征向量

步骤6：图像特征匹配

生成了两张图片的描述子后，最终对两张图片中的不同大小的描述子进行匹配。至此，完整的改进算法流程结束。

2.3 吊具位姿估计

改进算法最终应用在吊具位姿的估计上。实验的设计是基于手眼标定的基础上，即相机在吊具的前端，因此默认为吊具的位姿即相机的位姿。

首先使用上述算法流程中获得的所有立体匹配的特征点，然后利用最小化重投影误差来算出吊具的位姿。获取双目相机的标定参数，通过三角测量把图像的特征角点投影到三维空间中。假定0偏移情况下，则有：

在获取三维空间中的点与相机的投影点坐标之后，采用3D到2D的PnP方法求解吊具位姿R(r)和t，如图3所示。在世界坐标系下空间中有三点A、B和C，将其投影在平面上的点记做a、b和c，验证点记为D-d。

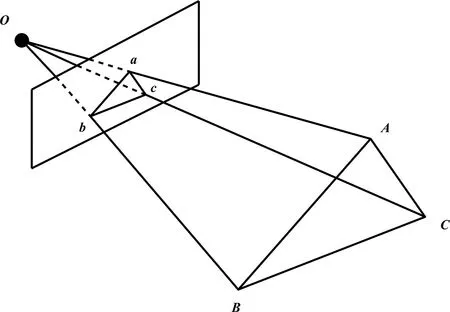
图3 P3P问题示意图

由于2D点在图像中的坐标位置已知，而利用世界坐标下的坐标可以计算出u、v、w的比值，这时只有x和y是未知变量。由于直接求解方程过于复杂，改用吴氏消元法求解[7]，求得四种解，最终获取到在相机坐标系下的三维坐标，并由此计算出吊具的位姿R和t。

为估计吊具的位姿，采用迭代最近点（ICP）进行求解。对ICP的求解使用Bundle Adjustment优化方法，通过构建最小二乘来获得最优解。假定三维空间中点P及投影点p有n个，求解吊具位姿R(r)和t，记它的李代数为ξ。设空间中点的坐标为Pi=[Xi,Yi,Zi]T，ui=[ui,vi]T代表投影点的像素坐标，则式(9)可变形为：

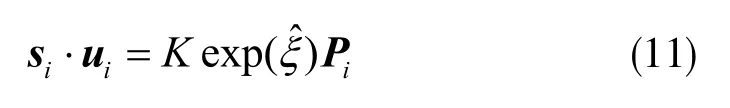
至此，用于表示吊具位姿的坐标在世界坐标系下的空间位姿的六个参数已全部得到,需进行实验，证明改进方法的可行性。

3 实验与结果分析

本实验使用Windows 10系统MATLAB R2019a为开发环境。首先通过实验来验证改进的立体算法的鲁棒性和实时性，分别选择不同尺度、不同旋转角度以及不同模糊程度的图像进行匹配，将原图像与待匹配图像进行匹配。改进算法与文献[8]算法的对比实验通过40幅图像、三种不同干扰情况来进行，对每组错误匹配率和耗时进行统计。

不同尺度变换图像的匹配结果如图4所示。

图4 不同尺度变换图像匹配结果

不同旋转角度变换图像的匹配结果如图5所示。

图5 不同旋转角度变换图像匹配结果

不同模糊程度变换图像的匹配结果如图6所示。

图6 不同模糊程度变换图像匹配结果

采用两种方法对40张图像进行了比较，并在不同的干扰条件下，分别计算了匹配率和算法耗时，详细比较结果如表1所示。

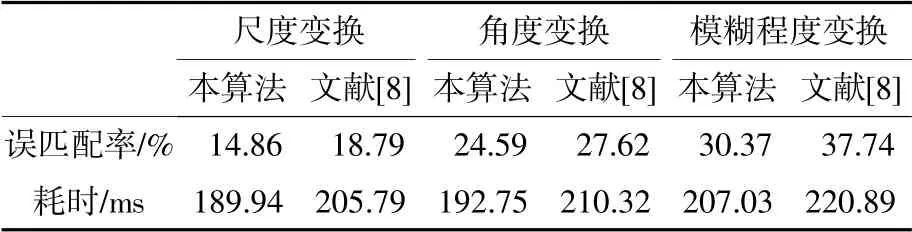
表1 不同干扰程度下匹配算法比较

结果表明，本算法对不同干扰的正确匹配率都比较高，从算法耗时比较的结果来看，此匹配算法所需时间明显减少，因此验证了改进的算法具有较好的鲁棒性。

由上述算法得出空间中的3个3D-2D对点，以及一对验证点，便可利用PnP算法求解出吊具的空间位姿。为验证此吊具位姿估计系统的检测精度，实验使用New Tsukuba数据集做测试实验。数据集包含了原始位姿，即Ground Truth Pose。

图7展示出利用改进算法和文献[8]算法构建的位姿结果。可以看出，改进算法求解出的位姿是较为精确的，有较强的实用性。

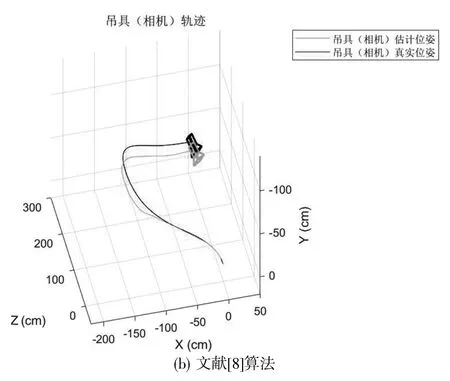
图7 吊具位姿检测实际效果

如表2所示为改进算法与文献[8]算法在平移误差、旋转误差以及运行时间上的比较。

表2 两种算法误差及耗时情况比较

可以看出本改进算法在平移误差、旋转误差以及运行时间上均优于文献[8]的算法，体现出了较强的适应性和鲁棒性。

4 结束语

本研究针对吊具位姿估计，通过对相机的标定和图像预处理等操作，基于Harris算子和极限约束，改进了SIFT立体匹配算法。在实验中，采用PnP方法求出的吊具位姿与实际符合较好，证明了研究的可行性。与其他算法相比，改进后的算法提高了匹配的效率和精度，可为后续吊具位姿匹配研究打下良好基础。