新型涡流槽密封泄漏特性与动力特性研究

姜金裕 孙 丹 赵 欢 张国臣 李 玉 温帅方

沈阳航空航天大学辽宁省航空推进系统先进测试技术重点实验室，沈阳，110136

0 引言

密封被广泛应用于各类透平机械中，具有防止工作介质泄漏、提高机组效率的作用[1]。近年来随着透平机械向高参数工况方向发展，密封能有效地防止气体泄漏，但同时也会有较大的气流激振力产生，从而引起密封的气流激振故障[2]。现有研究表明，由于进气预旋的存在而产生的交叉刚度是导致转子失稳的一个重要原因[3-5]。现有反预旋结构复杂且对泄漏特性及动力特性方面的改善效果不理想，因此开展新型密封结构研究、改善密封泄漏特性与动力特性具有很重要的工程价值。

ROSENGERG[6]最早发现了迷宫密封中气流的周向流动会引起密封内气流激振的现象。20世纪80年代，BENCKERT等[7]首次研究了密封进口处气体同转子转动方向流动对转子稳定性的影响，通过实验验证了向密封腔注入反向旋流可以降低密封交叉刚度。MUSZYNSKA等[8]提出了一种反预旋思想。目前有两种减小进气预旋的密封形式，一种是向密封腔室内注射与密封腔室内气流方向相反气体的反旋流密封。CHILDS等[9]和VANNINI等[10]通过实验研究了进口预旋对迷宫密封转子稳定性的影响机理，并指出降低进口预旋可以明显增加迷宫密封在高转速情况下的转子稳定性。KIM等[11]应用摄动理论研究数值方法分析了逆向射流对密封的转子稳定性产生的影响，结果表明反旋流的效果比径向进气要更加有优势。孙丹等[12]通过理论与实验研究了反旋流对密封泄漏特性与动力特性的影响，结果证明反旋流会降低密封刚度系数，增大密封阻尼系数。顾乾磊等[13]研究了进口预旋对密封系统静力与动力稳定性的影响，并分析了每个密封腔在不同预旋情况下切向气流力的变化影响。张衍等[14]数值与实验研究了反旋流注射的角度与位置对迷宫密封泄漏量影响的规律。虽然反旋流可以增加转子的稳定性，但是反旋流密封结构设计复杂，制作加工不易，且反向旋流引自主流，使主流流量损失，透平机械效率降低。反旋流密封虽然阻旋效果好，但是其结构复杂，设计难度大，而且若注入反向旋流强度过大，甚至会造成转子反向涡动，致使转子失稳，因此反旋流密封在实际应用中具有一定的局限性。

另一种形式便是在密封进口设置阻旋栅挡板的阻旋栅密封。NIELSEN等[15]通过实验研究了普通直型阻旋栅与流线型阻旋栅对密封动力特性的影响，研究发现，普通直阻旋栅密封具有更好的动力特性，同时发现密封长度增大后阻旋栅提高密封稳定性的作用不大。CHILDS等[16]进一步通过实验研究了无阻旋栅密封以及装配有直角、反旋流角三种阻旋栅的密封动力特性，对比发现，阻旋栅形状对密封直接阻尼和直接刚度影响有限，但能降低密封交叉刚度，提高密封稳定性。KWANKA[17]研究了不同密封在不同形式阻旋栅下的动力特性。吴可欣等[18]研究了阻旋栅位置和数量对密封模型的静力特性及模型在同一预旋比下的动力特性影响。虽然阻旋栅密封的结构较反旋流密封的简单，但是在高预旋比情况下，其结构对泄漏特性与动力特性的改善较小[19]。

针对预旋使迷宫密封产生气流激振力的问题，本文提出一种新型涡流槽密封结构，该种设计通过气体在槽内及槽的边缘产生涡流，降低周向的流动速度，进而达到抑制气流激振力的作用。本文建立了新型涡流槽密封静力与动力特性数值求解模型，研究了压比、预旋对不同涡流槽数量密封泄漏特性影响，在大预旋比情况下，涡流槽数量对密封动力特性的影响。

1 新型涡流槽密封设计思路

1.1 设计思路引出

迷宫密封中泄漏量计算公式为[20-21]

Mi=CiρiuiA

(1)

式中，Mi为质量流量；A为密封的横截面积；u为流速；Ci为流量系数；ρ为气流密度。

流量系数Ci的表达式为

(2)

(3)

式中,pi为第i个齿前后的压力；k为绝热指数。

(4)

则式(1)可写为

(5)

流体经过槽型结构会产生漩涡，使其流动受到阻碍，流体会克服该阻力耗散流体的能量，局部损失为

Δp=ρgh

(6)

(7)

式中，h为局部水头损失；Δp为局部压力损失；ξ为局部阻力系数，为量纲一系数，根据不同的局部装置而定。

根据式(6)、式(7)有

(8)

因为流体经过槽型结构可以降低进口压力，所以f(λi)降低，泄漏量下降。

1.2 新型涡流槽密封结构

本文提出一种具有涡流槽的新型密封结构，如图1所示。该新型密封结构为在传统迷宫密封的高压入口均匀设置有涡流槽结构，其中每个涡流槽与迷宫密封的第一个齿之间均具有一个独立的腔室。

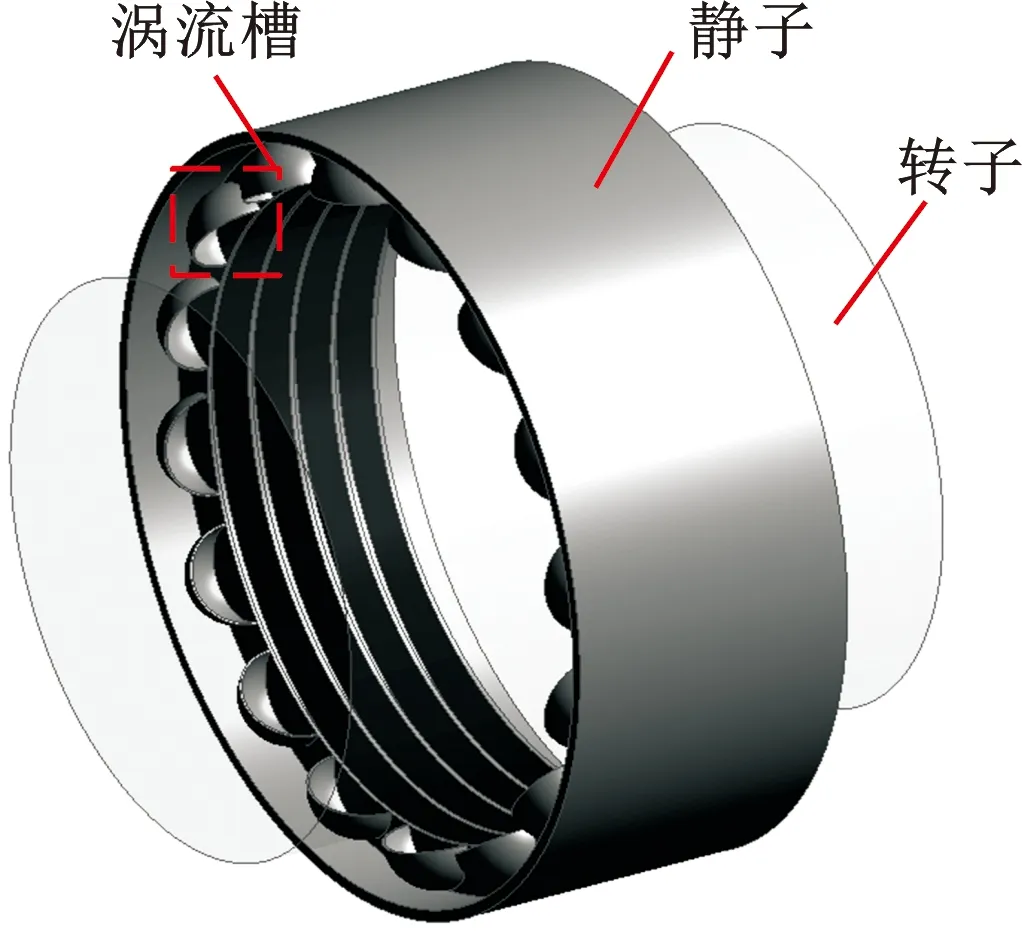
图1 新型涡流槽密封结构Fig.1 New type of vortex groove seal

密封结构在工作中，在进气口出现较大的预旋时，会对转子稳定性产生很大的影响。而涡流槽密封是在传统迷宫密封进口处均匀分布了同等大小的涡流槽结构，对密封的泄漏特性及动力特性均有所改善。

在泄漏特性方面，新型涡流槽密封的气流轴向流动如图2a所示，气流在进入密封前，先在涡流槽内对能量进行了一部分的耗散，从而达到减小泄漏量的目的。在动力特性方面，密封的周向流动如图2b所示，周向流动的气体会在涡流槽内部进行耗散，并且在靠近涡流槽的位置上会产生涡流，从而降低预旋的大小，达到提高转子稳定性的目的。

(a)新型涡流槽密封轴向气流流动图

2 密封动力特性理论研究

2.1 密封气流激振力线性化模型

图3所示为转子在密封中的椭圆轨迹涡动模型。

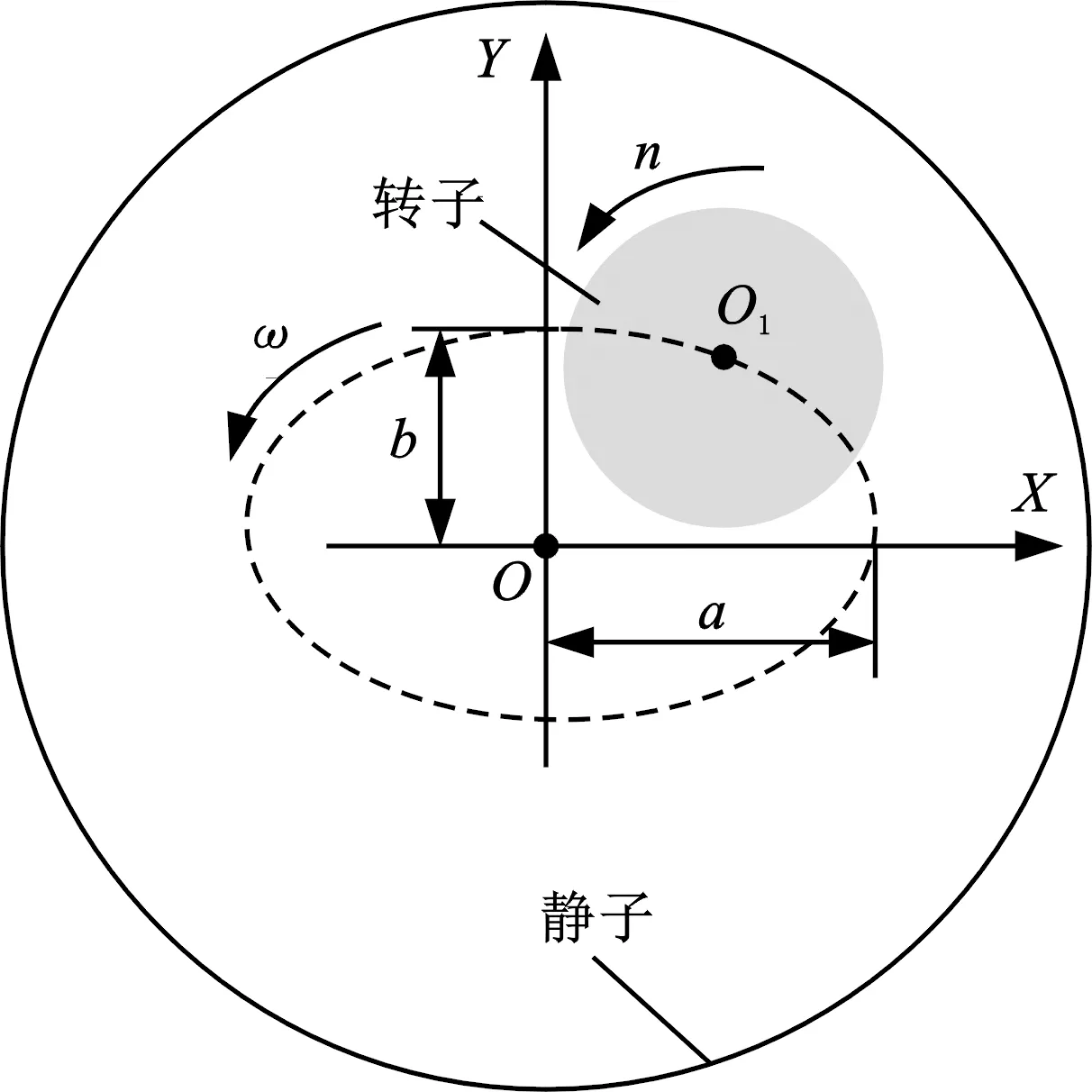
图3 椭圆轨迹涡动模型Fig.3 Vortex model of elliptical trajectory

图3中，ω为转子涡动的角速度，n为转子转速，O为密封静子中心，O1为转子系统中心。根据转子微小位移的涡动条件[22]，当转子绕密封静子中心做微小轨迹涡动时，转子此时受到的气流激振力Fx与Fy可用密封动力特性系数与小扰动量线性表示，表达式如下[23-24]：

(9)

2.2 转子多频椭圆涡动模型

转子在外部激励和自身不平衡的共同作用下，其涡动通常包含多个频率，本文采用多频椭圆涡动模型来求解密封动力特性系数，下面给出转子涡动方程。

X激励方向：

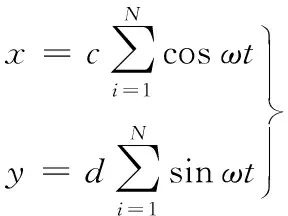
(10)

Y激励方向：

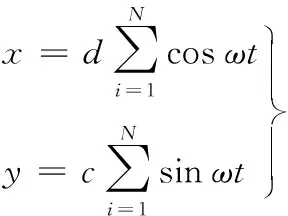
(11)

其中，ωi=2πfi，fi(fi=40 Hz，80 Hz，…，320 Hz)为转子涡动频率，c和d为转子的涡动幅值，N为转子涡动时所包含的频率数。为满足转子小位移涡动条件，即转子涡动振幅小于0.1倍的密封半径间隙，本文将转子涡动振幅设置为c=0.01Cr，d=0.005Cr，其中Cr为新型涡流槽密封的密封间隙。为获得转子在不同涡动频率下密封的动力特性系数，需将转子的涡动位移、速度和流体激振力的时域信号转化为频域信号，在频域内求解，将式(9)经傅里叶变换后可得频域内气流激振力与转子涡动位移之间的关系式：

(12)

式中，(ΔFx，ΔFy)和(Dx，Dy)分别是转子受到的气流力和涡动位移的频域信号。

将式(10)和式(11)代入式(12)可得

(13)

(14)

定义密封阻抗系数为

(15)

将式(15)代入式(13)、式(14)中，可得涡流密封的阻抗系数为

(16)

得到阻抗函数Hij后，则实部与虚部密封的刚度系数Kij与阻尼系数Cij为

(17)

3 新型涡流槽密封静力与动力特性数值求解模型

3.1 求解模型

涡流槽密封是在密封进口周向均匀布置有用来降低密封进口旋流速度及加快能量耗散涡流槽的新型密封，新型涡流槽密封结构如图4所示，第一个密封齿前周向均匀分布32涡流槽，沿轴向共有5个密封齿，4个密封腔室。本文主要对32槽、64槽的涡流槽密封与传统迷宫密封静力与动力特性进行对比研究。结构参数如表1所示。

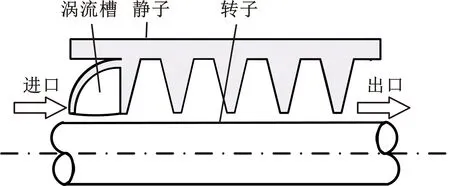
图4 涡流槽密封二维结构图Fig.4 Two-dimensional structure diagram of vortex groove seal

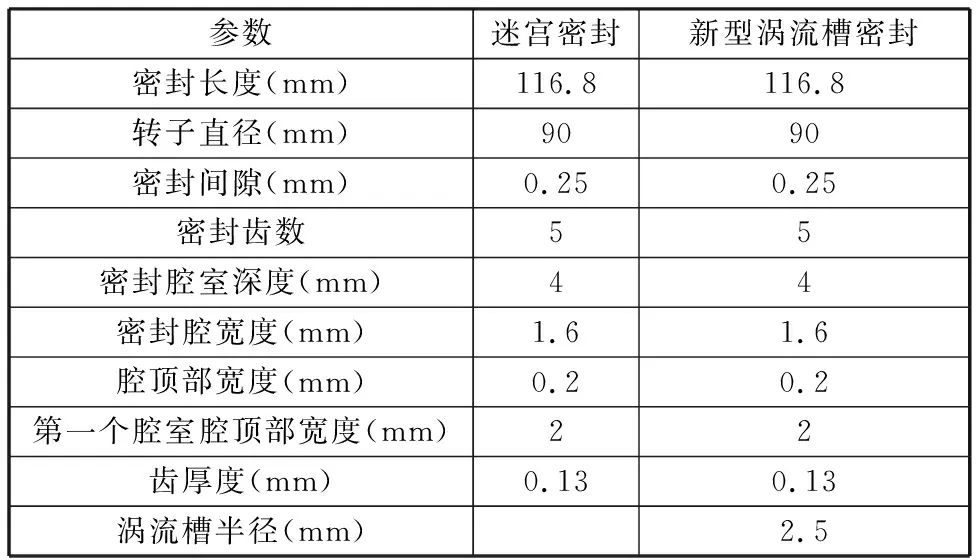
表1 密封模型几何尺寸

3.2 网格划分

本文提出的新型涡流槽密封求解模型采用四面体与六面体混合的网格划分方式，而所需对比分析的传统迷宫密封采用六面体网格划分方式。新型涡流槽数值模型经网格无关性验证后，最终确定设置流体域的周向节点为95个，密封腔室的轴向节点设置为40个，密封腔室流体域的径向节点设置为20个，齿顶间隙处的轴向节点设置为10个，密封的齿顶间隙处的径向节点设置为20个；对涡流槽部分的流体域采用四面体面网格画法，尺寸为0.3 mm，最终确定新型涡流槽密封的网格数为310万，确定传统迷宫密封的网格数为160万。图5所示为32槽新型涡流槽密封三维计算模型网格。

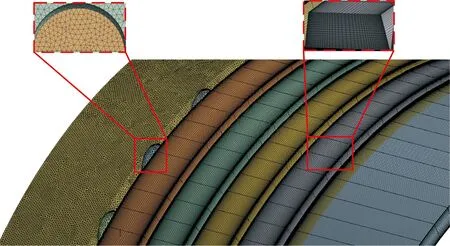
图5 网格划分Fig.5 Mesh mode of seal

3.3 边界条件

表2给出了本文求解模型的边界条件。进口设置为总压，出口设置为静压，进出口压比为3～6，温度为298 K，给定转子转速，工质选用为理想空气，湍流模型应用标准k-ε模型，近壁面区域采用改进壁面函数法，固定壁面设置为光滑、无滑移、绝热边界。

表2 边界条件

旋流比λ定义为气体在密封轴向某处沿径向截面的周向平均速度与转子面线速度之比，即

(18)

其中，v为密封周向面气流周向平均速度；r为转子半径。当v为密封进口面气流周向平均速度v0时，所求λ即为预旋比λ0。

本文分别对新型涡流槽密封、传统迷宫密封静力与动力特性进行计算分析，采用动网格方法来模拟转子的椭圆涡动轨迹。在定常计算过程中，转子不发生涡动，只绕轴心发生自转。涡动基频为40 Hz，涡动频率由40 Hz至320 Hz。当定常计算方程残差达到10-6数量级时认为计算收敛，非定常瞬态计算时，当转子所受气流力Fx、Fy波动曲线呈周期性且光滑，相邻两周期同一点的气流力相差小于0.2%时，认为非定常瞬态计算收敛。

3.4 数值方法准确性验证

为验证本文数值方法的准确性，根据试验台设计试验件，试验件的结构尺寸如图6所示，按照其尺寸建立模型并应用文本的数值方法计算，将数值计算结果与试验结果进行对比验证。

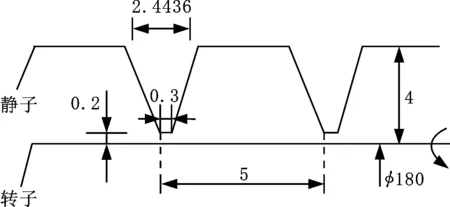
图6 密封模型几何尺寸(mm)Fig.6 Geometric dimensions of seal model(mm)

试验装置如图7a所示，该试验台的转子直径为180 mm，试验件密封的平均间隙为0.2 mm，试验转子转速为3000 r/min，设置压比为1～9，出口为大气压。气流由气罐流经安装有高精度流量计的管路进入到气缸内，利用数采系统实时同步采集进气流量数据。本试验台气缸设计为垂直进气，两端出气形式，如图7b所示，目的是使气流作用在气缸上的轴向推力互相抵消，并保证所有进入试验段的气体全部流经密封，使试验得到的泄漏量结果更加准确。试验测得无预旋进气工况下的泄漏量试验数据，并在相同工况下进行数值计算，将数值计算得到的结果与试验得到的结果进行对比。本文数值与试验所得泄漏量平均误差不超过15.7%，主要原因在于数值模型为轴向进气，而试验为气缸径向进气，气体进入气缸，轴向进入到密封入口段，轴向出气，模型存在简化，其次试验装置在安装过程中存在配合间隙误差，导致数值计算结果与试验结果存在一定误差，如图8所示。

(a)密封转子试验台

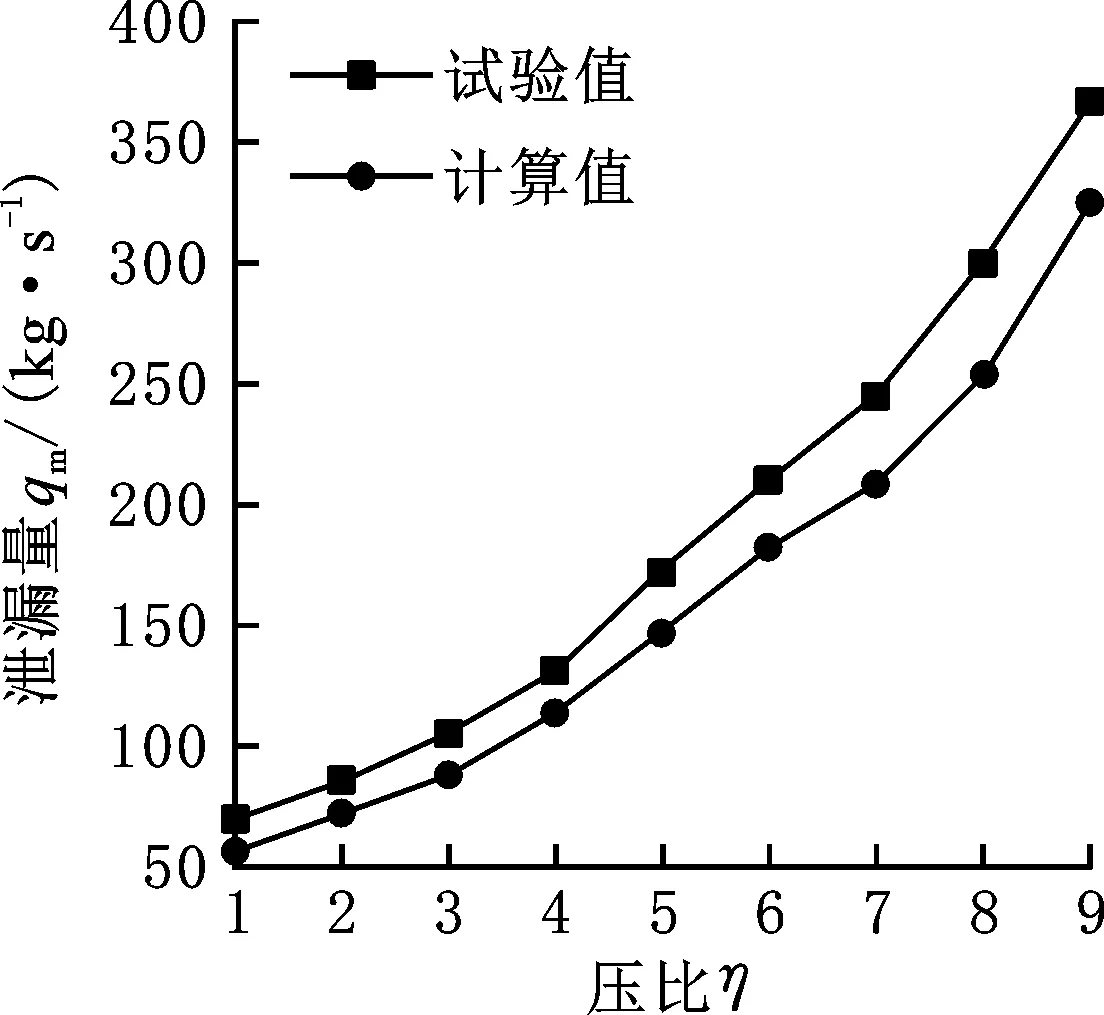
图8 数值计算和试验之间的泄漏结果比较Fig.8 Comparison of leakage results between numerical calculation and experiment

4 结果与分析

4.1 流场特性分析

图9为新型涡流槽密封在进口压力为0.6 MPa、出口压力为0.2 MPa、预旋比为0、转速为3000 r/min、涡流槽数量为32时的流场特性云图。图9a为新型涡流槽密封的中轴面压力分布云图，从图中可以了解到，气流沿着密封轴向方向，压力逐渐降低，且每个密封腔室内的压力几乎不发生改变。该现象产生的原因是气流在密封齿的齿顶与转子面之间密封间隙的位置发生节流效应，使气流流经间隙时流速增加，又因为气流在密封腔内形成涡流进行耗散，所以密封腔内的压力基本不发生改变，压力降低主要发生在密封的齿顶处。图9b为新型涡流槽密封的中轴面速度矢量图，从图中可以了解到，因为直通效应，密封中的一部分气流从密封间隙中流出，且气流的流速逐渐增大，另一部分气流由于转子的转动与进出口压差的原因，致使流体在新型涡流槽密封的腔室内形成较大的涡流，其中密封第一个密封齿前的涡流槽内也会形成涡流，加强流体能量的耗散。

(a)新型涡流槽密封轴向压力云图

4.2 新型涡流槽密封泄漏特性及影响机理分析

4.2.1新型涡流槽密封泄漏特性分析

图10示出了出口静压值为0.2 MPa、转速为3000 r/min、预旋比值为0时，新型涡流槽密封泄漏量随压比的变化关系。从图中可以了解到，压比不变时新型涡流槽密封泄漏量随涡流槽数量的增加而下降，且泄漏量随着压比的增大而增大；不同涡流槽数新型密封的泄漏量之间差值随着压比的增大而增大。

图11给出了进口压力为0.8 MPa、出口压力为0.2 MPa、转速为3000 r/min工况下不同涡流槽数量密封的泄漏量随预旋比变化规律。由图可以看出，预旋比不变的情况下新型涡流槽密封泄漏量随涡流槽数量的增加而下降。当预旋比改变时，新型涡流槽密封泄漏量随预旋比升高而降低，且预旋比越大，下降的趋势就越明显。

图11 泄漏量随预旋比变化的关系Fig.11 The relationship of leakage with prewhirl ratio

4.2.2涡流槽对密封泄漏特性影响机理分析

旋流强度K[25]可表征周向旋流大小与方向，反映了气流漩涡耗散作用的强弱，定义为

(19)

式中，vg为气体周向速度；vr为转子面周向速度。

图12 涡流槽流场周向截面提取位置示意图Fig.12 Schematic diagram of extraction location of circumferential section of flow field in the vortex grooves

本文以转子旋转方向为正向，分析涡流槽之间与涡流槽内流场旋流强度K值变化及漩涡耗散作用，揭示预旋对新型涡流槽密封泄漏特性影响机理。提取图12所示位置的涡流槽密封周向局部截面流场分布情况。图13给出了涡流槽数量为32的新型涡流槽密封进口气流周向流动状况，由图中可以看出，随预旋比增大，气流周向速度增大，两个相邻的涡流槽之间形成的涡流区越来越明显，且涡流槽内的涡流随着预旋比的增加也越来越明显，涡流区K值不断减小，预旋比增大到0.7时K值降至-1.04，说明漩涡强度增大，气流耗散作用增强，但是32个涡流槽彼此之间距离较远，涡流槽外涡流区只在紧靠涡流槽近处的区域出现，涡流槽之间的中间区域的气流漩涡耗散现象微弱，部分气流从涡流槽上的间隙流过，沿周向继续流动。图14示出了涡流槽数量分别为0、32、64且涡流槽密封在预旋比λ0=0.7时的进口气流周向流动状况，由图中可以看出，64个涡流槽沿周向分布更为紧密，两两涡流槽之间距离较32槽的距离减小，使气流周向分离现象减弱，涡流槽之间的气流方向改变，阻旋效果更加突出。当涡流槽数增大到64槽时，气流在涡流槽之间的涡流现象加强，涡流区K值最小为-1.25，相比于有32个涡流槽的密封涡流能量耗散增强，进一步减小泄漏量。

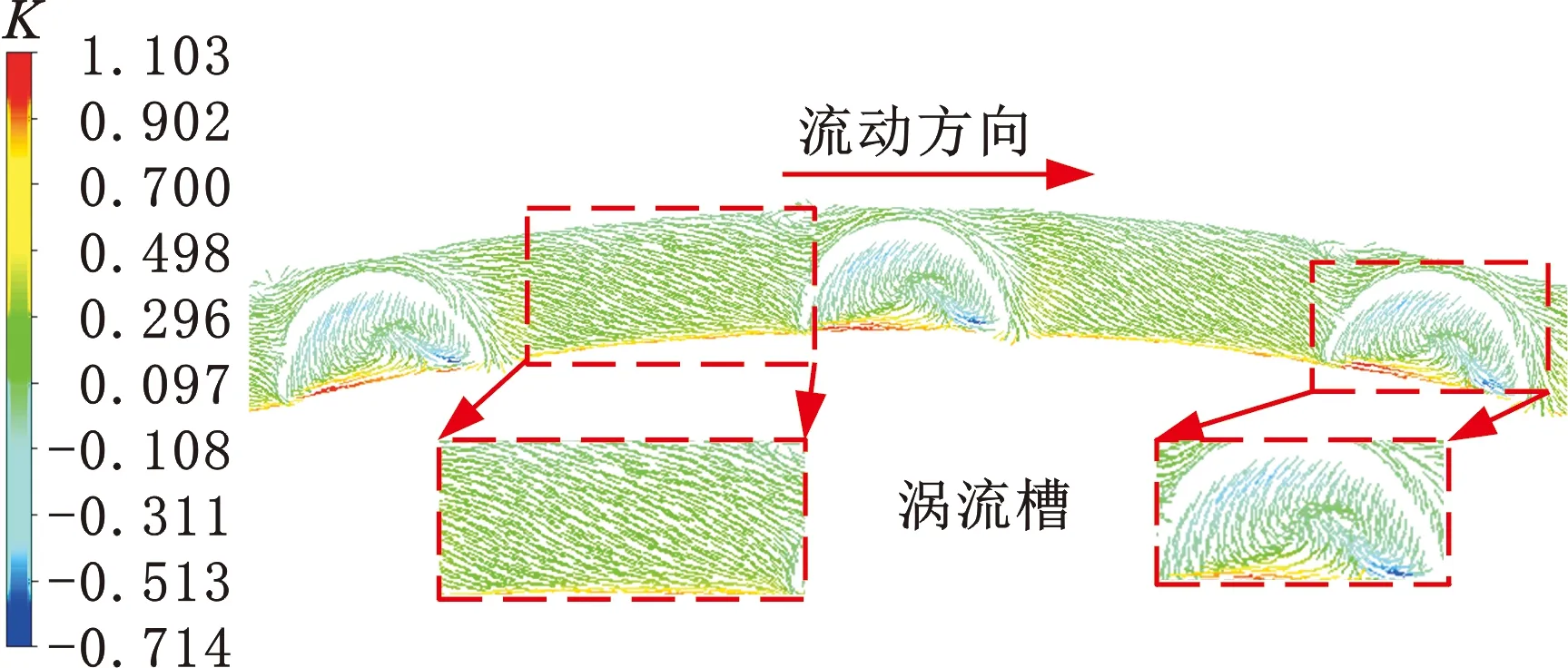
(a)λ0=0.3

(a)0 涡流槽 (b)32涡流槽 (c)64涡流槽图14 不同涡流槽数新型密封截面局部速度矢量图Fig.14 Local velocity vector of different vortex grooves for new seal section

4.2.3预旋对新型涡流槽密封进口位置旋流比影响分析

提取图12所示涡流槽密封位置截面的周向平均速度vt，分析多个预旋比下涡流槽密封该位置旋流比λt的变化。图15给出了新型涡流槽密封该位置截面的旋流比，由图中可以看出，传统迷宫密封腔室旋流比随预旋比增大而迅速增大，而新型涡流槽密封的周向截面旋流比在同一工况下较传统迷宫密封旋流比要小得多，旋流比的增大趋势更加平缓，而且涡流槽数量越多，同一预旋比下的周向旋流比更小。在预旋比λ0=0.5时，传统迷宫密封的旋流比为λt=0.526，而32涡流槽密封的旋流比为λt=0.175，64涡流槽密封则更小，旋流比为λt=0.07。相互比较可得出，64涡流槽密封比32涡流槽密封的旋流比下降了60%，比0涡流槽密封的旋流比下降了86.6%。在预旋比λ0=0.7时，迷宫密封的旋流比为λt=0.705，32涡流槽密封的旋流比为λt=0.231，64涡流槽密封更小，其旋流比为λt=0.102。64涡流槽密封比32涡流槽密封的旋流比下降了67.2%，比传统迷宫密封密封的旋流比下降了85.5%。

图15 不同涡流槽数密封周向截面旋流比变化图Fig.15 Variation diagram of swirl ratio of seal circumferential section with different number of vortexgrooves

4.3 新型涡流槽密封动力特性及影响机理分析

4.3.1新型涡流槽密封动力特性结果分析

图16给出了进口压力0.8 MPa、出口压力0.2 MPa、转速3000 r/min、预旋比0.7工况下，不同涡流槽数量新型密封的直接刚度系数随涡动频率的变化规律。由图中可以看出，直接刚度值随涡动频率增加而减小，且在同一涡动频率下，直接刚度随着涡流槽数量的增大而增大。图17给出了不同涡流槽数量新型密封的交叉刚度系数随涡动频率的变化规律，从图中可知，当频率从40 Hz增大到120 Hz时，交叉刚度的值随着涡动频率的增大而减小，新型涡流槽密封交叉刚度比传统迷宫密封的交叉刚度更小，当频率从120 Hz增大到320 Hz时，交叉刚度值随着频率的增加而增大，且在相同频率下，交叉刚度值随着涡流槽数量的增加而降低。

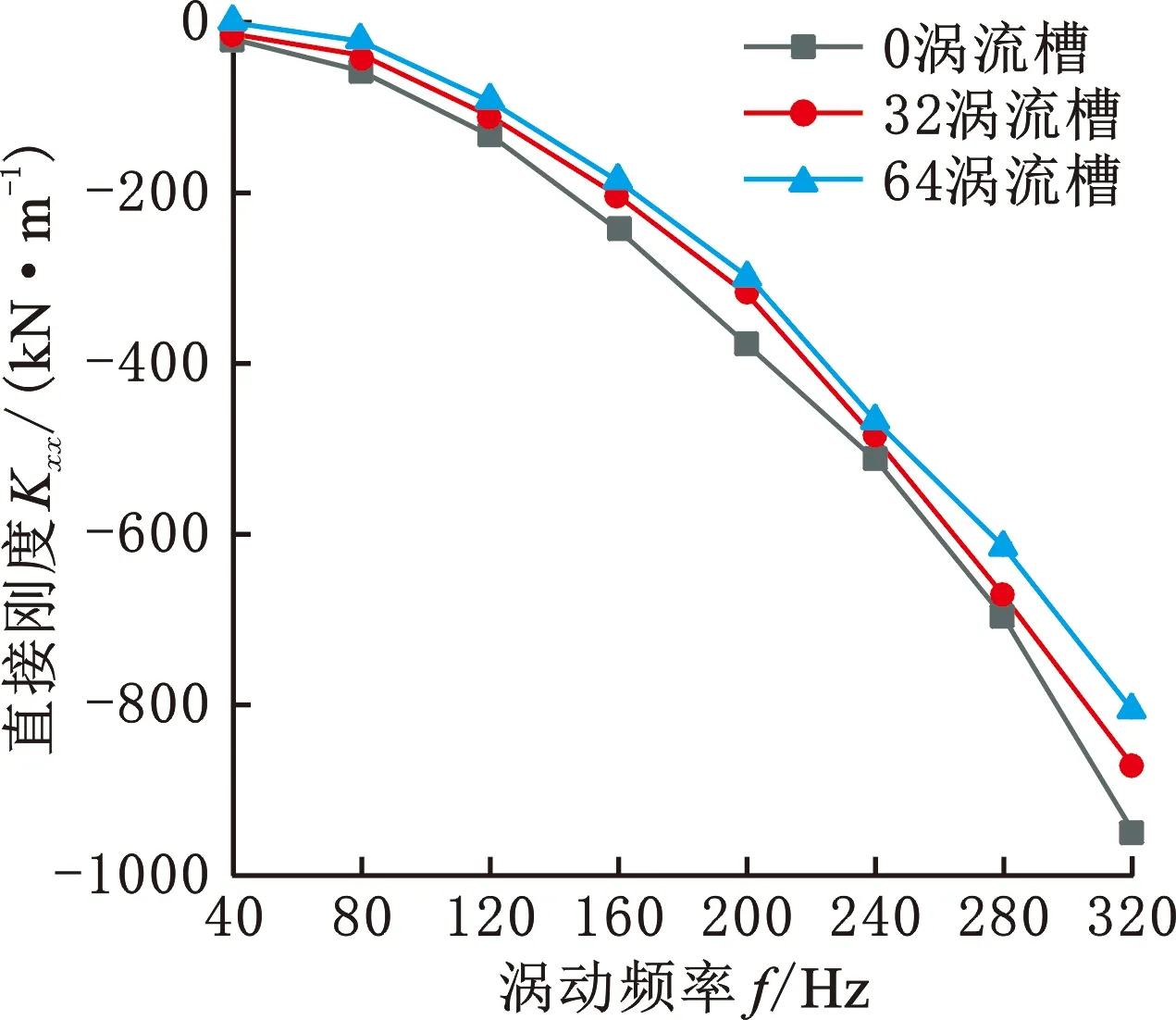
图16 直接刚度变化图Fig.16 Variation diagram of direct stiffness

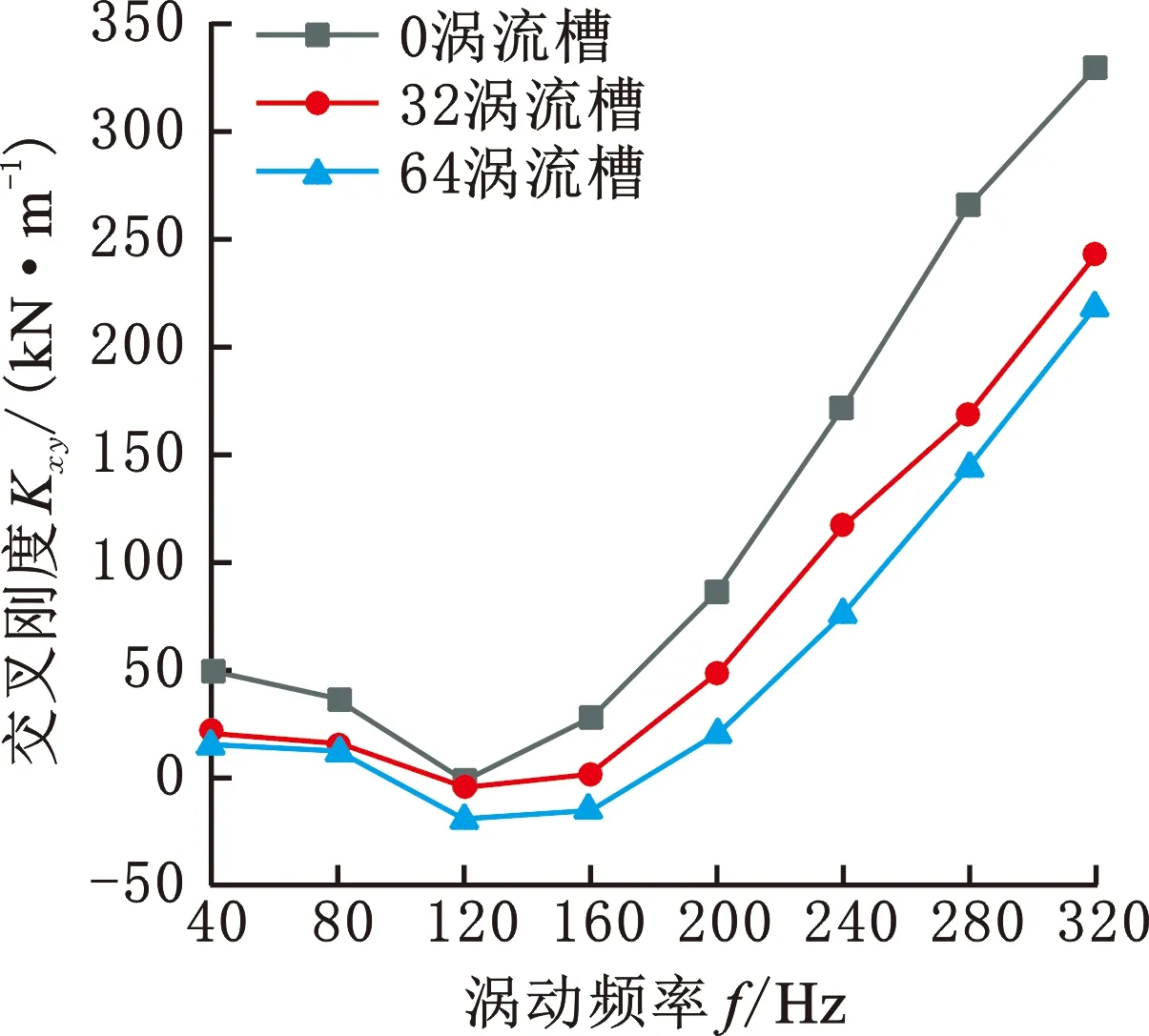
图17 交叉刚度变化图Fig.17 Variation diagram of cross stiffness

图18给出了这三种涡流槽数量密封的直接阻尼随涡动频率改变的变化情况，由图中可以看出，随着涡动频率的增大，这三种涡流槽数量密封的直接阻尼均先减小后增大，当频率低于120 Hz时，直接阻尼随着涡动频率的增大而减小，当涡动频率大于120 Hz时，直接阻尼随着涡动频率的增大而增大。在同一涡动频率下，直接阻尼随着槽数的增加而增大。图19给出了交叉阻尼变化情况，由图中可以看出，交叉阻尼随涡动频率的增加均先增加后减小，当涡动频率不变的情况下，随着涡流槽数目的增加，密封的交叉阻尼系数增大。

图18 直接阻尼变化图Fig.18 Variation diagram of direct damping

图19 交叉阻尼变化图Fig.19 Variation diagram of cross damping

4.3.2新型涡流槽密封转子稳定性分析

引入有效刚度Keff与有效阻尼Ceff系数评价涡流槽密封转子动力特性稳定性[26]，即

Keff=Kxx+Cxyω

(20)

Ceff=Cxx-Kxy/ω

(21)

有效阻尼与有效刚度计算结果分别如图20、图21所示。图20给出了这三种涡流槽数量密封的有效阻尼变化趋势，由图中可以看出，预旋比为0.7时，三种涡流槽数量密封有效阻尼系数大小随着涡动频率的增大而增大，三种涡流槽数密封结构的有效阻尼均为正，均对转子系统的涡动起到了抑制作用，且在同一频率下，涡流槽数量增大会提高密封有效阻尼。图21给出了有效刚度随频率变化，由图中可以看出，三种涡流槽数量密封在0.7预旋比下，随着涡动频率的增大，直接刚度逐渐降低，且在同一预旋比时，涡流槽密封的有效刚度随着涡流槽数的增加而增大。

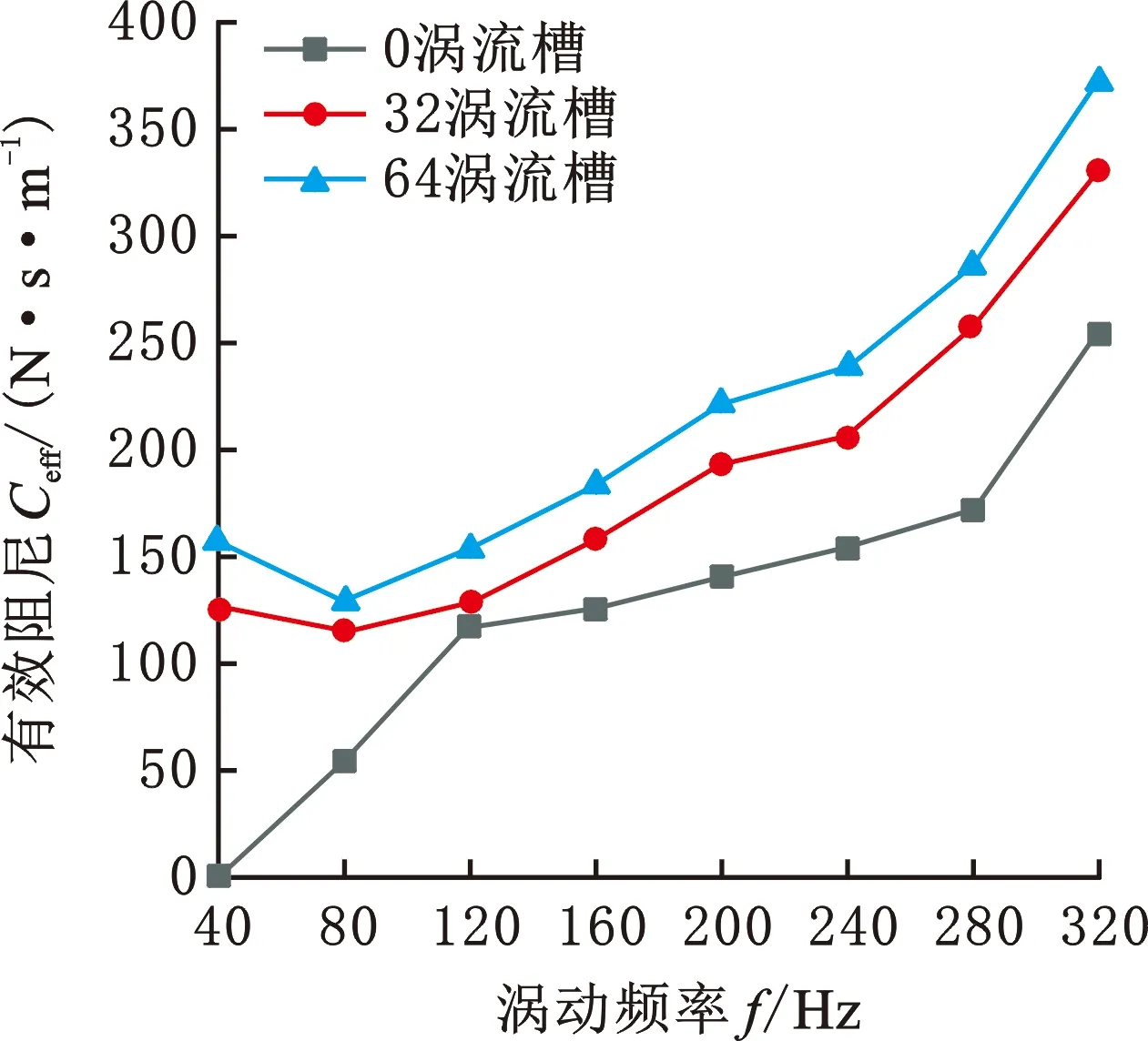
图20 有效阻尼变化图Fig.20 Variation diagram of effective damping

图21 有效刚度变化图Fig.21 Variation diagram of effective stiffness

4.3.3涡流槽对密封动力特性影响机理分析

为研究涡流槽数量对密封动力特性的影响机理，提取涡流槽密封第一个腔室位置的截面周向压力分布，分析在0.7预旋比情况下，不同涡流槽数量对该位置的截面周向压力的影响。图22为不同涡流槽数量密封转子所受激振力矢量与压力云图。由式(9)可得

(22)

Ft=-CeffD

(23)

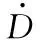
由图22中可以看出，这三种密封径向力Fr与涡动方向相同，随着涡流槽数量的增加，径向力Fr逐渐减小，由式(22)可知，有效刚度增加。随着涡流槽数量的增加，切向力Ft逐渐增大，且均与转子涡动速度反向相反，由式(23)可知，有效阻尼增大能抑制转子涡动，有利于转子系统的稳定。

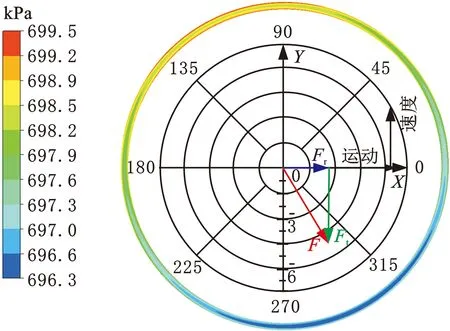
(a)0涡流槽

5 结论

(1)随着涡流槽数量的增加，新型涡流槽密封的泄漏量逐渐降低，且随着压比的升高，泄漏量的差距逐渐增大。当密封进出口压比为6时，64涡流槽的密封比传统迷宫密封泄漏量下降了3.37%。

(2)随着涡流槽数量的增加，新型涡流槽密封的交叉刚度减小，直接刚度、直接阻尼与交叉阻尼增大，有效阻尼和有效阻尼也均增大，且有效阻尼随着涡动频率的增大而增大，有效刚度随着涡动频率的增大而减小。

(3)新型涡流槽密封的切向气流力随着涡流槽数目的增加而增大，且方向与转子涡动速度方向相反。三种密封的有效阻尼随着涡流槽数量及频率的增大而增加，均为正值，对转子系统的涡动起到了抑制作用。