基于机器学习的石油装备用大截面高强韧马氏体钢智能设计与性能研究

李方坡 路彩虹 赵靖宵 李秀程 尚成嘉

1.中国石油集团工程材料研究院有限公司石油管材及装备材料服役行为与结构安全国家重点实验室，西安，7100772.北京科技大学钢铁共性技术协同创新中心，北京，10083

0 引言

我国深层油气资源丰富，陆上主要的剩余石油天然气资源均分布在深层超深层，开发利用前景广阔。我国西部近10年来增长的油气储量中，约90%来自于埋深超过4500 m的深层超深层，加强深层超深层油气资源的勘探开发对保障我国能源安全具有重要意义[1]。“十三五”以来，我国深井超深井数量不断增加，7000 m/8000 m/9000 m/12 000 m钻机先后投入我国油田现场，石油装备关键承载构件安全余量越来越小，截面尺寸越来越大。低碳马氏体钢作为我国自主开发的石油装备用钢，也是目前石油装备用材料中强度等级最高的钢种，具有优异的强韧性和疲劳性能，可大幅减小装备构件质量，延长使用寿命，实现服役性能与制造经济性的完美结合[2]。为确保马氏体钢构件的全截面整体性能优异，材料必须具有足够的淬透性，目前我国在用低碳马氏体钢的最大淬透直径约为120 mm，已无法满足截面直径达150 mm甚至更大截面装备构件的制造需求，迫切需要开发具有淬透性和强韧性更好且满足150 mm直径全截面淬透的马氏体钢新材料。

随着材料信息学的发展，材料数据库、数据挖掘及机器学习等手段被应用于新材料的开发。借助理论模型、机器学习及材料大数据，针对目标需求优化传统材料的成分-工艺调控组织与性能的新方法方兴未艾[3-4]。近年来，机器学习方法在材料领域获得广泛应用，国内外许多研究者通过机器学习方法建立了材料成分-性能或成分-结构预测模型[5-9]。机器学习算法种类繁多[10]，主要包括决策树[11]、人工神经网络[12]、支持向量机[13]和随机森林[14]等，不同算法各有千秋。受制于材料研究过程中实验条件的复杂性，现阶段大部分研究的数据样本都源自实验数据或文献数据，样本容量有限，而且不同试验条件下的数据间误差较大，这对材料设计模型的准确性产生不利影响[15]。

为了解决大截面高强韧马氏体钢成分最优化的难题，本文根据石油装备用高强韧马氏体钢的成分要求，基于计算获得的数百万组不同成分性能数据分别建立不同机器学习方法的成分-性能预测模型并进行对比研究，依据产品性能要求，设计开发出满足性能的最优成分，并进行产品试制和性能研究，以实现大幅缩短石油装备构件用马氏体钢新材料的研发周期和研发成本。

1 机器学习模型优化与结果评价

1.1 数据采集及预处理

基于前期石油装备构件产品生产制造和性能需求，初步选择待开发马氏体钢的化学成分及性能分布范围，见表1。计算获得661组不同成分实验材料的淬透性试验数据，每组数据包括成分信息和距表面不同位置处的洛氏硬度和屈服强度。本文选择直径为150 mm的马氏体钢圆棒，分别建立针对圆棒心部位置洛氏硬度和屈服强度的机器学习预测模型。为消除原始数据中不同输入特征数值差距对模型的影响，对输入特征数值进行归一化处理：

(1)

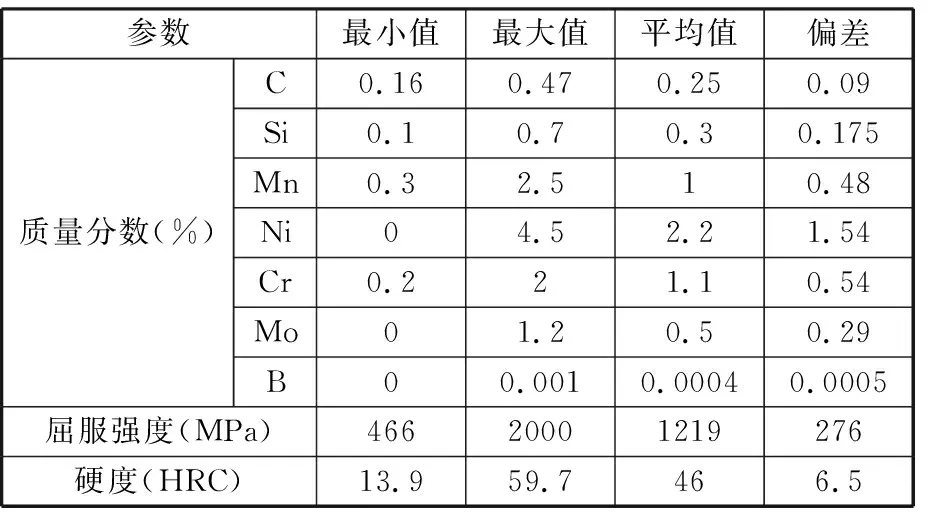
表1 材料的化学成分与性能分布

1.2 学习模型的选择

为确定在本数据集上表现最佳的机器学习预测模型，采用支持向量机回归(support vector machines for pattern recognition，SVR)、人工神经网络(artificial neural network，ANN)、随机森林(random forest，RF)和梯度提升回归机(gradient boosting regression，GBR)四种不同的机器学习方法分别建立成分-屈服强度和成分-洛氏硬度回归预测模型。为了提高机器学习模型的精度，通过使用不同训练参数建立模型并对比最终性能的方式获得模型精度最高时的训练参数，同时避免模型产生严重的过拟合，将获得的参数作为模型训练过程中的最佳参数。

1.3 学习模型的评价

为了定量描述和比较机器学习模型的预测误差，采用平均绝对误差(mean absolute error，MAE)与均方误差(mean square error，MSE)来定量表示机器学习模型的预测性能，其计算公式分别为

(2)

(3)

(a)MAE

(a)MAE

四种模型预测值与计算值分布散点图见图3。随着模型预测精度提高，数据点分布将更加集中在y=x这条直线上，由图3可见，ANN模型中的数据点与y=x直线间的吻合程度最高。综上，选择ANN模型作为材料屈服强度和洛氏硬度的预测模型和遗传算法的目标函数。

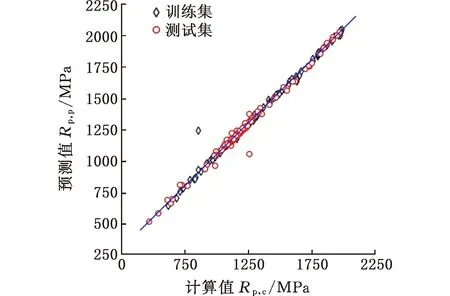
(a)ANN

1.4 学习模型参数的优化

ANN模型复杂度受神经网络拓扑结构的影响，为进一步提高ANN模型精度，对ANN模型中隐含层数量及对应的神经元节点数进行优化，并采用拟牛顿法解决非线性优化，获得更快的收敛速度和更高的预测精度。ANN模型在预测屈服强度时不同神经元层数和层深的具体表现如图4所示。由图4可见，当神经元层数为4、层深为64时，神经网络的预测精度最高同时拟合程度最好；神经元层数为3、层深为32时，由于模型结构简单，导致平均绝对误差MAE偏大；然而当神经元层数为4、层深为128时，模型在训练集上MAE最低，但是与测试集偏差较大，出现了过拟合现象，因此最佳的ANN结构确定为64×64×64×64。

图4 不同层数和层深条件下的ANN模型性能Fig.4 The performance of different hidden layersand layer depth of ANN

1.5 马氏体钢成分优化

成分-性能机器学习模型建立后，采用第二代非支配排序遗传算法(non-dominated sorting genetic algorithms,NSGA-Ⅱ)计算同时满足屈服强度与洛氏硬度需求的优化成分，实现两个目标的高通量优化[16]。精英策略指在保留父代的前提下，通过让父代和经过选择、交叉、变异后产生的子代共同组成一个群体，避免父代中可能存在的最优解被遗落，最后经过再次选择操作，获得与初始种群同样规模的群落。本文采用的NSGA-Ⅱ算法流程如图5所示。基于ANN预测模型初步优化的材料成分变化范围见表2，初始种群规模设定为100，利用建立的机器学习模型依据成分选择范围生成100个第一代种群，并对每个成分数据进行预测，获得屈服强度和洛氏硬度预测值。对种群中不满足要求的成分个体进行淘汰，重新对初代种群进行选择、交叉、变异，直到数量达到初始种群数量。利用最近欧拉距离解来计算100个解的拥挤度和适应度，然后通过对目标值和拥挤度的评价和排序，获得第一代集合的Pareto前沿。利用遗传算子从第一代亲本染色体中产生后代，遗传算子对第一代结合中解的信息存储链进行选择、交叉和变异，以产生新的解。运用精英策略选择材料成分最优解的第二代集合，通过循环迭代，在代与代之间逐渐优化产生最优解。设置进化代数为400，直到进化至400代便停止进化。最终获得CrNiMo系和SiMnCrNiMo系两种马氏体钢材料系的最优成分个体，对应的材料成分见表3。

图5 第二代非支配排序遗传算法的优化流程Fig.5 Optimization process of NSGA-Ⅱ

表2 化学成分与力学性能分布

表3 优化的材料成分与性能

2 实验验证与性能研究

为检验这种成分优化方法的可行性及机器学习模型的准确性，按照表3的两种成分分别冶炼试验钢，并根据国家标准GB/T 225进行端淬试验。首先经过920 ℃正火处理，随后加热至900 ℃，保温30 min，出炉后立即在端淬试验机上进行顶端冷却，并在5～90 mm(间距为5 mm)范围内检测试验钢的洛氏硬度，获得的淬透性曲线如图6所示。对比端淬试验获得的淬透性曲线、计算值曲线及预测值曲线，可以看出淬透性曲线的预测值与实验值非常接近，最大误差不超过3HRC，说明计算获得的淬透性结果具有较高的精度，这也为针对目标性能的成分逆向优化设计提供了依据。

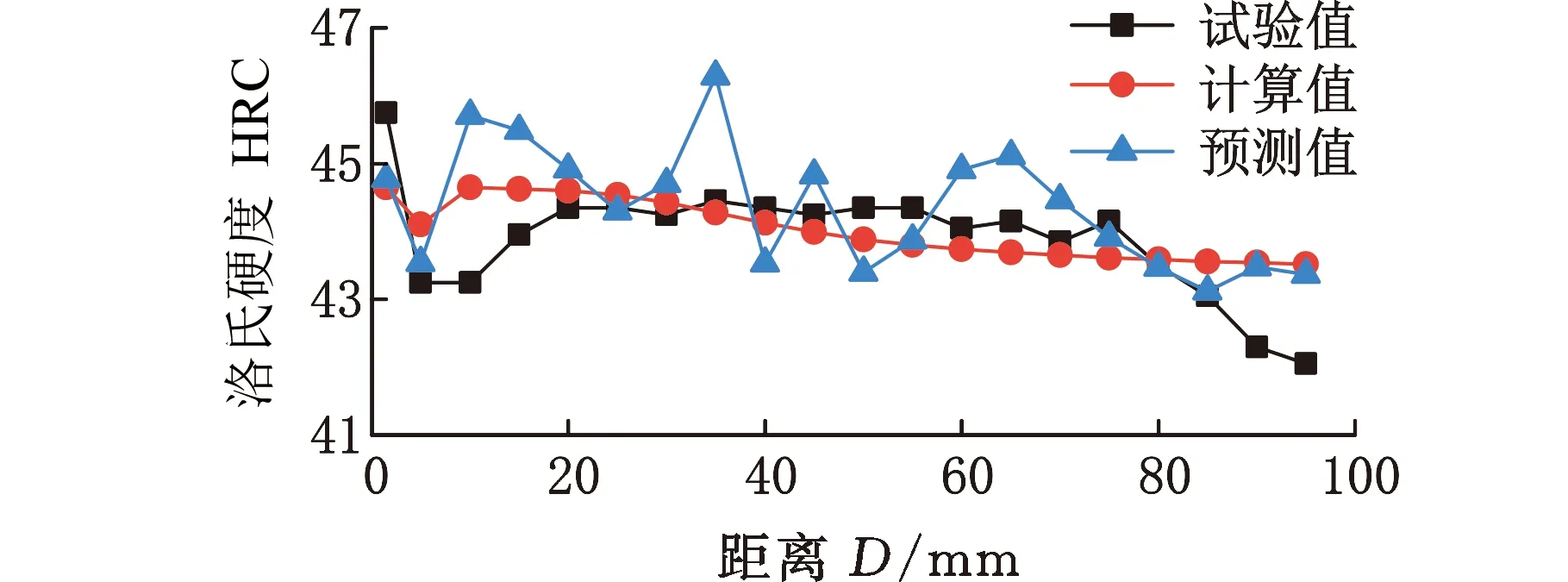
(a)材料1

(a)强度

依据优化设计的成分累计完成多批次马氏体钢冶炼，并生产制造截面直径150 mm的构件产品，结合马氏体钢材料成分及相变温度参数对材料热处理工艺进行系统优化，获得构件产品强韧性匹配最优的热处理工艺流程为正火+高温回火+淬火+低温回火，并据此工艺流程对产品进行相应热处理。分别对产品的屈服强度和冲击韧性指标进行检测分析，检测结果如图7所示，可见产品的屈服强度均在1100 MPa以上，抗拉强度均在1400 MPa以上，冲击吸收能均在45 J以上，产品的强度和韧性指标均高于产品设计要求。对产品构件全直径截面组织进行检测分析后发现，从表面至心部组织均主要为细小的针状马氏体组织，马氏体含量达到95%以上，贝氏体和残余奥氏体含量小于5%，实现了构件产品的全截面马氏体转变，如图8所示。马氏体组织的含量和状态决定了马氏体钢的强韧性，马氏体含量越多，晶粒越细，获得强韧性越好，这也是开发本材料的初衷。

(a)表面 (b)1/2半径

3 结论

(1)分别采用4种不同机器学习算法建立了低碳马氏体钢成分-强度及成分-硬度预测模型，研究结果表明神经元层数为4、层深为64的人工神经网络模型针对石油装备构件用低碳马氏体钢成分体系预测精度最高、拟合程度最好。

(2)采用遗传算法对材料成分进行智能最优化设计，获得CrNiMo和SiMnCrNiMo两种材料系中屈服强度大于1100 MPa、硬度大于42HRC、碳含量小于0.22%的最优成分，材料的端淬硬度分布曲线与预测模型值基本一致，最大误差小于3HRC。

(3)依据优化设计成分进行多批次产品生产制造结果表明，150 mm直径的构件产品全截面获得95%以上的细小针状马氏体组织，屈服强度均大于1100 MPa，低温冲击吸收能大于45 J，满足服役性能要求，预测结果与生产实验结果具有较高的一致性。