多维动态贝叶斯网络及其重要度分析方法
陈东宁 胡彦龙 姚成玉 王宽通 马 雷
1.燕山大学河北省重型机械流体动力传输与控制重点实验室,秦皇岛,0660042.先进锻压成形技术与科学教育部重点实验室(燕山大学),秦皇岛,0660043.燕山大学河北省工业计算机控制工程重点实验室,秦皇岛,066004
0 引言
贝叶斯网络(Bayesian network, BN)又称信度网络,由PEARL[1]在20世纪80年代提出。贝叶斯网络是由表示变量的节点和表示节点之间关系的有向边组成的有向无环图,常用于分析复杂的、不确定的可靠性问题。传统静态贝叶斯网络只能分析静态逻辑关系,难以刻画动态逻辑关系,因而动态贝叶斯网络逐渐被国内外学者广泛研究[2-3]。动态贝叶斯网络分为离散时间贝叶斯网络和连续时间贝叶斯网络。文献[4]针对动车组列控中心系统故障具有多态性和动态性的问题建立离散时间贝叶斯网络的分析方法,通过重要度和敏感性分析方法对动车组列控中心系统进行可靠性分析。虽然离散时间贝叶斯网络分析方法可以描述事件静动态失效行为,但在可靠性求解过程中存在计算误差。连续时间贝叶斯网络分析方法可以弥补上述不足,且能够得到失效概率随时间的连续变化趋势[5]。文献[6]采用连续时间贝叶斯网络进行动态系统可靠性建模和分析,为解决复杂系统可靠性、敏感性和不确定性建模问题建立了一种新的方法。
连续时间贝叶斯网络虽然提高了计算精度,但是无法对受多因素影响的复杂系统进行可靠性分析。目前关于可靠度受多因素影响的可靠性分析文献较少。文献[7]定义了多维空间故障树的相关概念,并研究了电气系统在使用时间和使用温度两个因素影响下,相关各故障概率空间的构造过程。文献[8]将可靠度多影响因素引入到T-S动态故障树中,提出连续时间多维T-S动态故障树,进一步提高了T-S动态故障树的建模能力。
重要度分析方法可以量化基本元件对系统失效的影响程度,是寻找系统薄弱环节的基本方法,在可靠性分析中应用广泛[9]。文献[10]提出了关键重要度和概率重要度的概念,分别用来评价基本事件组成结构的关键度和基本事件可靠性变化对系统可靠性的影响度。文献[11]在传统T-S故障树基础上引入了模糊理论,并提出T-S模糊重要度概念及其计算方法。文献[12]在多维T-S故障树分析方法的基础上,提出了多维T-S故障树概率重要度和关键重要度分析方法,并将所提方法应用在电气、机械系统上,验证了所提方法的优越性。
本文针对传统贝叶斯网络分析方法仅能分析时间单因素影响的问题,在传统贝叶斯网络分析方法的基础上进行时间连续化构造与多维扩展,提出多维动态贝叶斯网络分析方法,该方法能够对系统在诸如冲击、温度变化等复杂工况下进行可靠性分析,使可靠性模型更接近于实际。并进一步给出多因素影响下的根节点后验概率、概率重要度和关键重要度计算公式,为系统薄弱环节的发现提供依据。
1 多维动态贝叶斯网络分析方法
1.1 贝叶斯网络时间连续化构造
将贝叶斯网络时间连续化时需借助于单位阶跃函数与冲激函数来描述根节点的时序关系与叶节点的失效时刻[5]。
(1)单位阶跃函数。单位阶跃函数在进行积分运算过程中会转化为积分的上下限,用来表示事件的失效顺序。单位阶跃函数定义为
(1)
式中,ti、tj分别为根节点xi、xj的失效时刻;u(ti-tj)为单位阶跃函数,表示根节点xi、xj的失效时序。
(2)冲激函数。利用冲激函数来描述叶节点的失效时刻,冲激函数定义为
(2)
其中,tT表示叶节点T的失效时刻,冲激函数δ(ti-tT)=∞表示叶节点T在根节点xi的失效时刻ti发生失效,即tT=ti;δ(ti-tT)=0表示叶节点T在根节点xi的失效时刻ti不发生失效,即tT≠ti。
1.2 多维动态贝叶斯网络叶节点失效概率
假设根节点xi(i=1, 2, …,n)除了受时间因素影响外还受m个影响因素(e1,e2,…,em)的共同影响,且各因素间相互独立,则根节点xi的失效概率分布函数Fi(ti,e1,e2,…,em)为

(3)
式中,Fi(ti)为仅受时间影响下根节点xi的失效概率分布函数;Fj(ej)为受ej因素影响下根节点xi的失效概率分布函数。
通过对根节点xi失效概率分布函数各因素求偏导,可以得到根节点xi的失效概率密度分布函数fi(ti,e1,e2,…,em)为
(4)
由根节点xi的失效概率密度函数,可求得叶节点T在时间因素和除时间因素外m个影响因素(e1,e2,…,em)的共同影响下的失效概率密度分布函数fT(tT,e1,e2,…,em)为
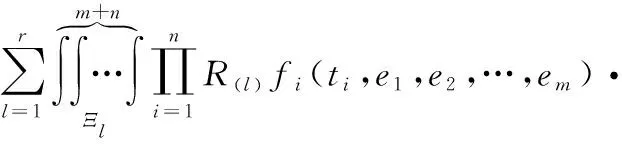
(5)
式中,r为条件概率表序号;Ξl为序号l下的积分域;R(l)=u(ti-tj)表示序号l的顺序规则;i、j表示任意两个节点;P(l)(tT)为序号l下描述叶节点T的冲激函数。
由叶节点T失效概率密度分布函数fT(tT,e1,e2,…,em)可得叶节点T失效概率分布函数FT(tT,e1,e2,…,em)为

(6)
1.3 多维动态贝叶斯网络根节点后验概率
根据贝叶斯网络可以反向推理这一特点,可计算出多维动态贝叶斯网络在叶节点失效的情况下中间节点或根节点在任务时间内的后验概率。多维动态贝叶斯网络后验概率公式为
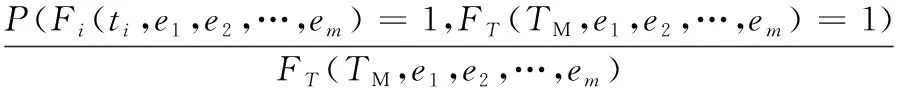
(7)
式中,FT(TM,e1,e2,…,em)为叶节点T在任务时间TM内的失效概率。
2 多维动态贝叶斯网络重要度分析方法
重要度分析方法是系统可靠性分析的重要部分,目前尚缺少受多因素影响条件下系统元件重要度的分析方法,为此,本文在传统故障树重要度分析方法和多维动态贝叶斯网络分析方法的基础上,提出多维动态贝叶斯网络重要度分析方法。
2.1 多维动态贝叶斯网络概率重要度
概率重要度是由学者BIRNBAUM[10]在20世纪60年代首次提出的概念,是应用最广泛的重要度分析方法之一,表示系统中组件或基本部件失效状态变化影响系统失效概率变化的程度。基于此,本文提出多维动态贝叶斯网络概率重要度。
多维动态贝叶斯网络根节点概率重要度IPr(xi)定义为叶节点T失效概率分布函数对根节点xi失效概率分布函数的偏导数,其计算公式为
(8)
式中,FT(ti,e1,e2,…,em)表示叶节点T受时间和其他多种因素影响下的失效概率分布函数;Fi(ti,e1,e2,…,em)表示根节点xi受时间和其他多种因素影响下的失效概率分布函数。
2.2 多维动态贝叶斯网络关键重要度
概率重要度没有考虑基本元件失效的速率以及变化的难易程度,而关键重要度表示系统中某一组件或部件失效概率变化率与其引起系统失效概率变化率的比值。
多维动态贝叶斯网络根节点xi的关键重要度ICr(xi)表示为多因素影响下根节点xi失效概率变化率与其引起叶节点T失效概率变化率的比值,其计算公式为
(9)
3 实例分析与验证
斗轮机是重要的物料装卸设备,其张紧机构的作用是为悬臂带式输送机张紧装置提供张紧压力[13]。本文用所提出的多维动态贝叶斯网络及重要度分析方法对斗轮机张紧机构液压系统进行可靠性分析,并与离散时间贝叶斯网络分析结果进行对比验证。
3.1 失效概率分析
斗轮机张紧机构液压系统液压原理如图1所示。根据斗轮机张紧机构液压原理图,利用DUGAN等[14]创立的动态故障树分析方法,建立张紧机构液压系统Dugan动态故障树,如图2所示。

1,2.压力继电器 3.液压泵 4.溢流阀 5.单向阀6,7.张紧液压缸 8.过滤器 9.液压油10.蓄能器 11.电磁换向阀 12.冷却器图1 斗轮机张紧机构液压原理图Fig.1 Hydraulic schematic diagram of tensioningmechanism of bucket wheel machine
在图2所示的Dugan动态故障树中,G2表示功能相关门,G4表示热备件门,G5表示优先与门,其他均表示为或门,元件寿命分布服从指数分布,底事件名称及失效率如表1所示,中间事件及顶事件表述内容如表2所示。
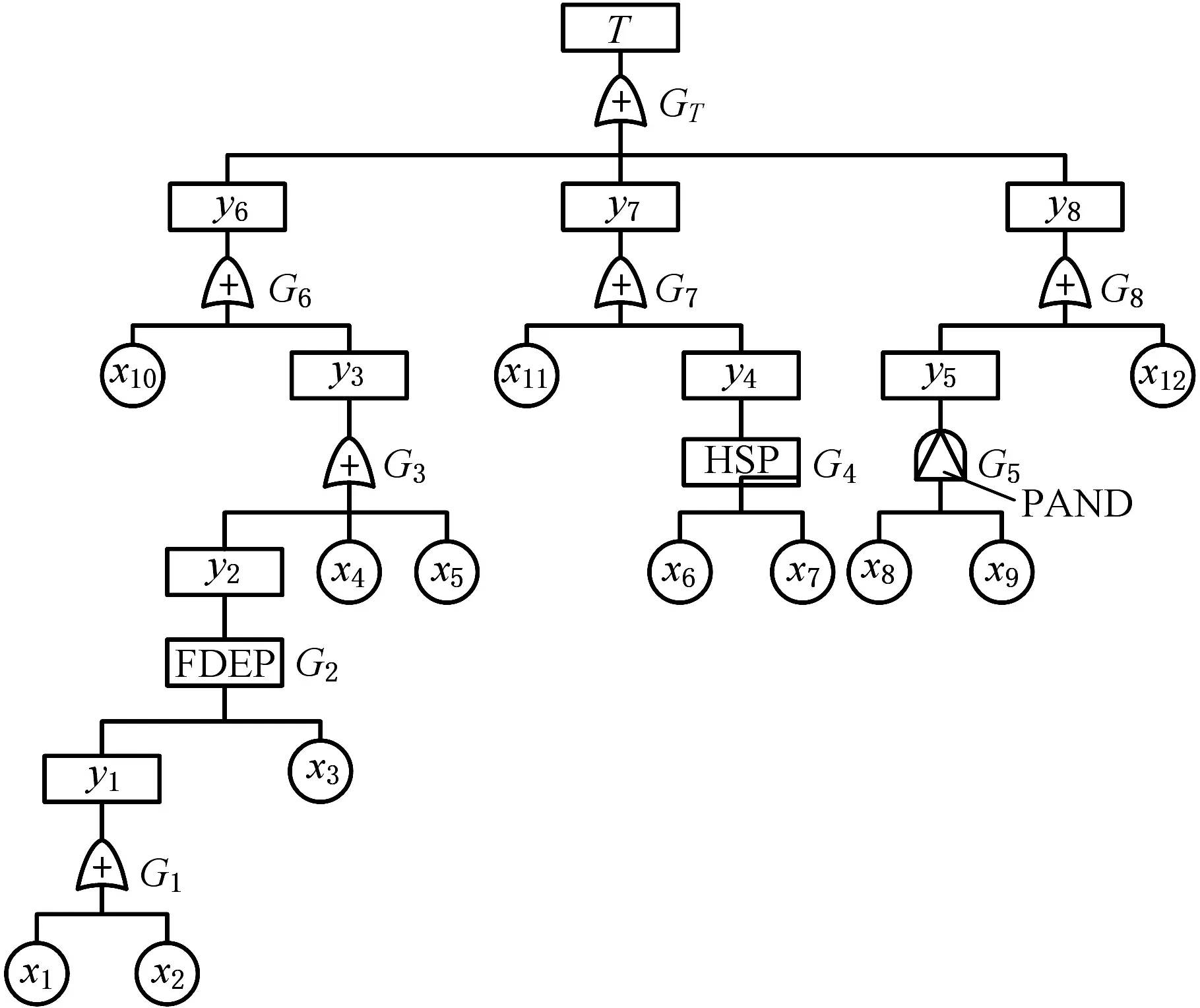
图2 张紧机构液压系统Dugan动态故障树Fig.2 Dugan dynamic fault tree of hydraulic system oftension mechanism

表1 基本事件及失效率

表2 中间事件表述内容
在张紧机构中,溢流阀和液压泵寿命受作业过程中液压冲击影响较大,令所受冲击影响服从威布尔分布,其参数数据如表3所示。

表3 基本事件威布尔参数
将图2所示的张紧机构Dugan动态故障树转化为相应的多维动态贝叶斯网络,如图3所示,设定任务时间为10 000 h。
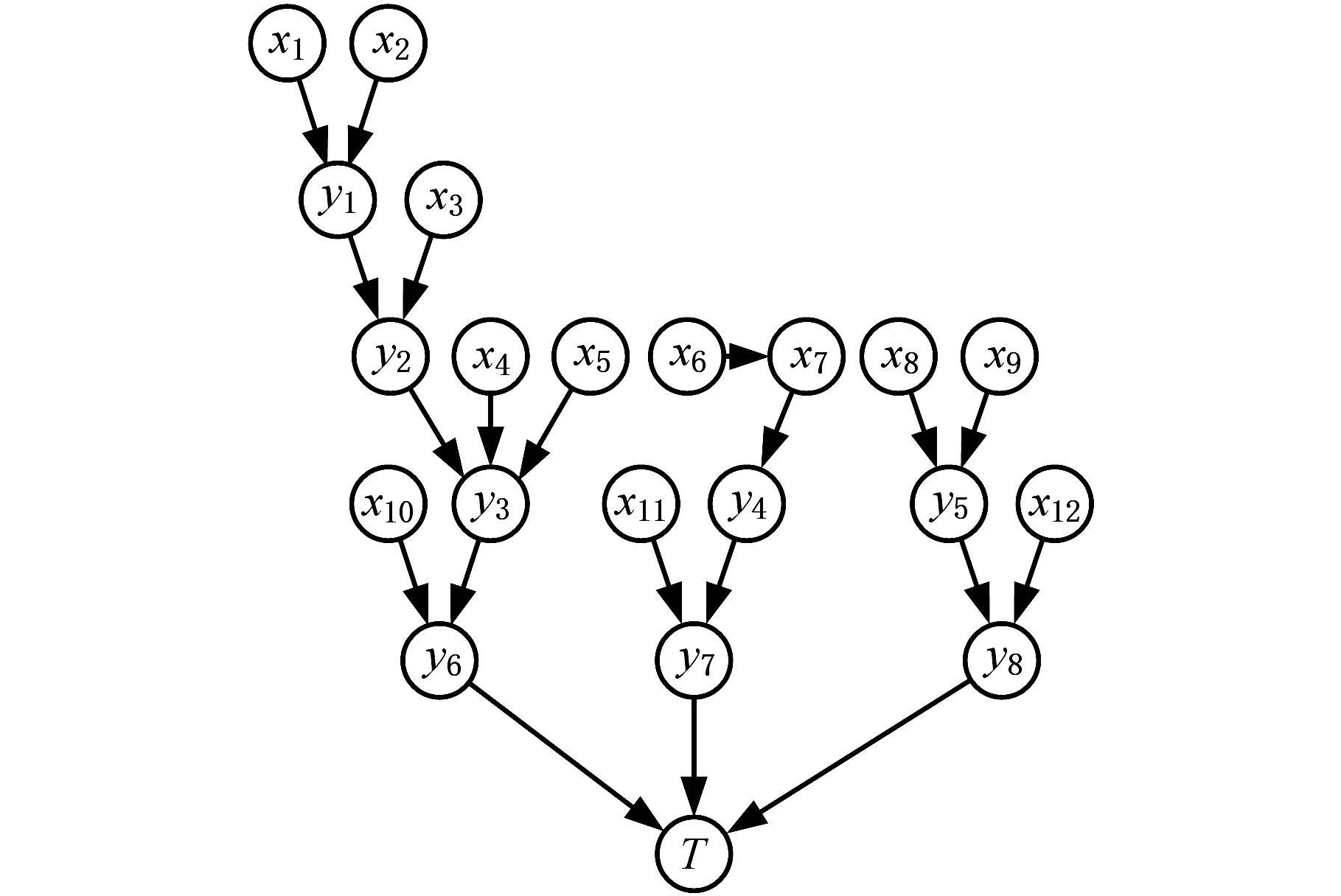
图3 张紧机构液压系统多维动态贝叶斯网络Fig.3 Multi-dimensional dynamic Bayesian network ofhydraulic system of tension mechanism
3.1.1叶节点失效概率
(1)离散时间贝叶斯网络分析方法。将任务时间划分为5段,由离散时间贝叶斯网络分析方法求得图3中叶节点T在各段时间内失效概率,如表4所示。由表4可知,叶节点T在任务时间内失效概率为0.3971,在任务时间外失效概率为0.6029。

表4 叶节点T在各个时间段的失效概率
(2)多维动态贝叶斯网络分析方法。首先分析式(5)中G1、G2、G4、G5动态门对应的R(l)和P(l)。
根节点x1、x2与节点y1组成的G1门为或门,其规则为:R(1)=u(t2-t1),表示根节点x1失效在先、x2失效在后,冲激函数P(1)=δ(t1-ty1)表示节点y1的失效时刻发生在根节点x1的失效时刻t1;R(2)=u(t1-t2)表示根节点x2失效在先、x1失效在后,P(2)=δ(t2-ty1)表示节点y1的失效时刻发生在根节点x2的失效时刻t2。
G2门为功能相关门,其规则为:R(1)=u(t3-ty1),P(1)=δ(ty1-ty2);R(2)=u(ty1-t3),P(2)=δ(t3-ty2)。
G4为热备件门逻辑关系,其规则为:R(1)=u(t7-t6),P(1)=δ(t7-ty4);R(2)=u(t6-t7),P(2)=δ(t6-ty4)。
G5为优先与门逻辑关系,其规则为:R(1)=u(t9-t8),P(1)=δ(t9-ty5);R(2)=u(t8-t9),P(2)=0。由多维动态贝叶斯网络计算公式(式(3)~式(6)),仅考虑系统失效概率受工作时间影响时,可求得叶节点T随工作时间t的失效概率变化曲线,如图4所示。由图4可知,当任务时间为10 000 h时,叶节点T在任务时间内失效概率为0.3971,与表4离散时间贝叶斯网络分析方法的计算结果相同。

图4 叶节点T随工作时间的失效概率分布Fig.4 Failure probability distribution of leaf nodeT with working time
考虑系统失效概率受工作时间与液压冲击共同影响时,可求得叶节点T失效概率在多因素影响条件下的分布情况,如图5所示。由图5可见,考虑系统失效概率受工作时间与液压冲击共同影响时,多维动态贝叶斯网络分析方法可以显示失效概率随工作时间t和冲击次数c的变化趋势,更有优势。

图5 叶节点T随工作时间和冲击次数的失效概率分布Fig.5 Failure probability distribution of leaf node T withworking time and numbers of shocks
3.1.2根节点后验概率
仅考虑工作时间影响时,通过离散时间贝叶斯网络和多维动态贝叶斯网络分析方法可以求得图3中贝叶斯网络根节点任务时间内后验概率,如表5所示。考虑系统失效概率受工作时间与液压冲击共同影响时,由式(7)可以求得图3中斗轮机张紧机构多维动态贝叶斯网络的根节点后验概率,如图6所示。由图6可知,多维动态贝叶斯网络分析方法可以显示根节点xi后验概率随工作时间和冲击次数的变化趋势,且整体大小排序与离散时间贝叶斯网络后验概率相同,即由大到小依次为x3、x11、x10、x4、x5、x1=x2、x9、x12、x8、x6=x7。

表5 根节点xi后验概率

图6 根节点xi后验概率分布Fig.6 Root node xi posterior probability distribution
3.2 重要度分析
本文利用离散时间贝叶斯网络分析方法和所提多维贝叶斯网络根节点重要度分析方法对斗轮机张紧机构液压元件作重要度对比分析。
(1)概率重要度。仅考虑工作时间影响时,利用离散时间贝叶斯网络与多维贝叶斯网络分析方法可以求得斗轮机张紧机构液压元件任务时间内概率重要度,如表6所示。

表6 根节点xi概率重要度
考虑系统失效概率受工作时间与液压冲击共同影响时,可以求得斗轮机张紧机构液压元件多维概率重要度分布曲线,如图7所示。

图7 多维概率重要度Fig.7 Multi-dimensional probability importance
在图7中,多维概率重要度由大到小的顺序与离散时间贝叶斯网络重要度相同,且能描述概率重要度随多因素变化趋势,整体大小排序为x3、x11、x10、x4、x5、x1=x2、x12、x8、x9、x6=x7。
(2)关键重要度。仅考虑工作时间影响时,利用离散时间贝叶斯网络与多维动态贝叶斯网络分析方法可以求得斗轮机张紧机构液压元件任务时间内关键重要度,如表7所示。

表7 根节点xi关键重要度
考虑系统失效概率受工作时间与液压冲击共同影响时,求得斗轮机张紧机构液压元件多维关键重要度数值分布曲线,如图8所示。

图8 多维关键重要度Fig.8 Multi-dimensional criticality importance
在图8中,多维关键重要度数值由大到小排列顺序为x3、x11、x10、x4、x5、x1=x2、x12、x8、x9、x6=x7。
综合后验概率、概率重要度和关键重要度分析结果,分析斗轮机张紧机构可知,x3(液压泵)、x11(电磁换向阀)、x10(蓄能器)的重要度较大,当系统失效时可以优先排查这些元件是否出现故障。
由上述重要度分析结果可得,多维动态贝叶斯网络重要度分析方法所求结果整体大小排序与离散时间贝叶斯网络分析方法所求结果大小排序一致。仅考虑工作时间影响时,多维动态贝叶斯网络分析方法求得的根节点重要度与离散时间贝叶斯网络分析方法计算结果几乎相同。多维动态贝叶斯网络重要度分析方法可以分析系统受工作时间t和冲击次数c共同影响时基本元件重要度问题,还可以显示重要度随工作时间t和冲击次数c的变化趋势,所以更有优势。
4 结论
考虑实际系统中可靠性影响因素的多维性,结合连续时间贝叶斯网络分析方法的优势,借助单位阶跃函数与冲激函数进行贝叶斯网络时间连续化构造,推导了根节点受多因素影响时系统的失效概率分布函数,并对传统重要度分析方法进行多维扩展,提出了多维动态贝叶斯网络及其重要度分析方法。以斗轮机张紧机构液压系统为对象,与离散贝叶斯网络分析方法进行对比分析,验证了多维动态贝叶斯网络及重要度分析方法的可行性与优越性,为考虑多因素影响时的可靠性建模提供了新的方法。

