基于干扰观测器的X舵AUV零纵倾变深控制

李 杨，韩俊庆，缪旭弘，徐雪峰

(1. 海军研究院，北京 100161；2. 天津航海仪器研究所九江分部，天津 300131)

0 引 言

自主水下航行器（AUV）相比于其他类型的水下平台，具有活动范围大、机动性好、安全、智能化等优点，在海底铺管、海底勘测、水下设备维修与维护等方面得到了广泛的应用。如今随着AUV执行任务的复杂度越来越高，对AUV的操纵性能要求也越来越高。相比于十字舵，X舵具有更高的操纵性，并且具有横滚控制能力，是未来AUV尾舵的发展趋势。

然而，由于X舵特殊的布置方式，每个舵面都具有纵倾与航向的控制功能，相比于十字舵，X舵的控制方式不直观，AUV在进行变深控制时，很难兼顾水平面运动以及保证AUV以小纵倾方式平稳变深，因此研究一种有效的X舵AUV零纵倾变深操纵控制方法尤为重要。

目前，对于变深控制的大部分研究工作都是针对十字尾舵的AUV。杨德成等针对AUV在舵角与舵速约束下的深度控制问题提出一种基于模型预测控制的AUV深度控制方法，仿真结果表明该方法具有良好的动态控制性能。霍江航等针对AUV运动过程中水动力参数摄动与外界干扰问题，基于L1自适应理论提出一种AUV深度控制器，仿真结果表明该控制器拥有良好动态响应的同时能够保证抗干扰能力与鲁棒性。绕志荣等针对AUV在外部扰动与内部扰动下深度难以控制的问题，提出一种基于干扰观测器的自适应终端滑模控制方法，仿真结果表明此方法有着很强的抗干扰性。

本文根据十字舵AUV深度控制器的设计思路，提出一种X舵AUV的变深控制方法。该方法利用非线性干扰观测器来补偿深度与纵倾通道的耦合干扰与未建模动态，并设计深度与纵倾双通道耦合控制器，使首舵与尾舵联合控制深度与纵倾，提高深度与纵倾的控制精度，达到零纵倾变深的目的。设计X舵舵角分配算法，将尾舵指令分配到4个舵角上。仿真实验验证了该算法的有效性。

1 模型描述

由于AUV垂直面的运动与水平面的运动之前耦合作用很小，在研究变深控制问题时可忽略水平面运动，因此在AUV六自由度标准模型基础上进行简化，得到AUV垂直面的非线性动力学模型如下：

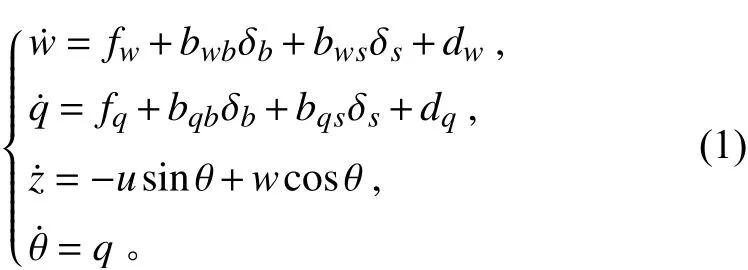
式中：，，，θ分别为AUV的垂向速度、纵倾角速度、深度和纵倾角；为AUV的纵向速度，变深航行时一般保持纵向速度不变；δ为AUV的首舵舵角，δ为AUV的虚拟尾舵舵角，可由X舵的4个舵角转化得到；d与d为AUV变深运动时垂向与纵倾通道的耦合干扰与未建模动态，其余参数项的表达式如下：

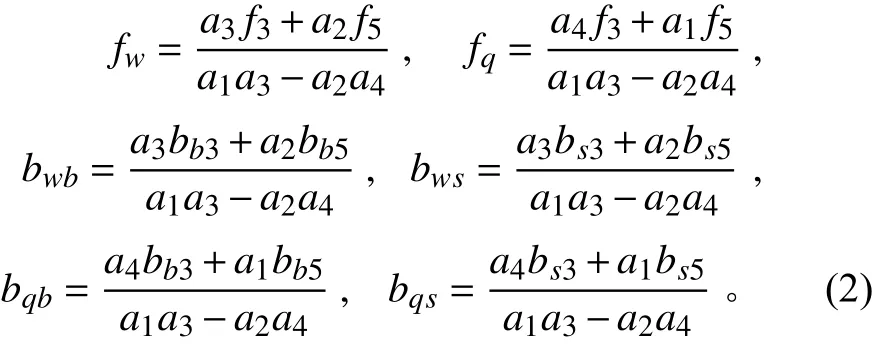
式中，各个动力学系数分别为：

式中：为AUV的浮力，为 AUV质量，为AUV长度，ρ为海水密度，其余参数为水动力参数。

2 控制器设计

本文的控制器设计分为3个部分：1）设计非线性干扰观测器，估计并补偿变深时深度与纵倾通道的耦合干扰与未建模动态；2）设计双通道耦合滑模控制器，实现AUV的零纵倾高精度变深控制，并引入饱和函数来替代符号函数，消除滑模控制的抖振问题；3）设计X舵舵角分配率，将尾舵指令分配到X舵的4个舵上。控制器的结构形式如图1所示。

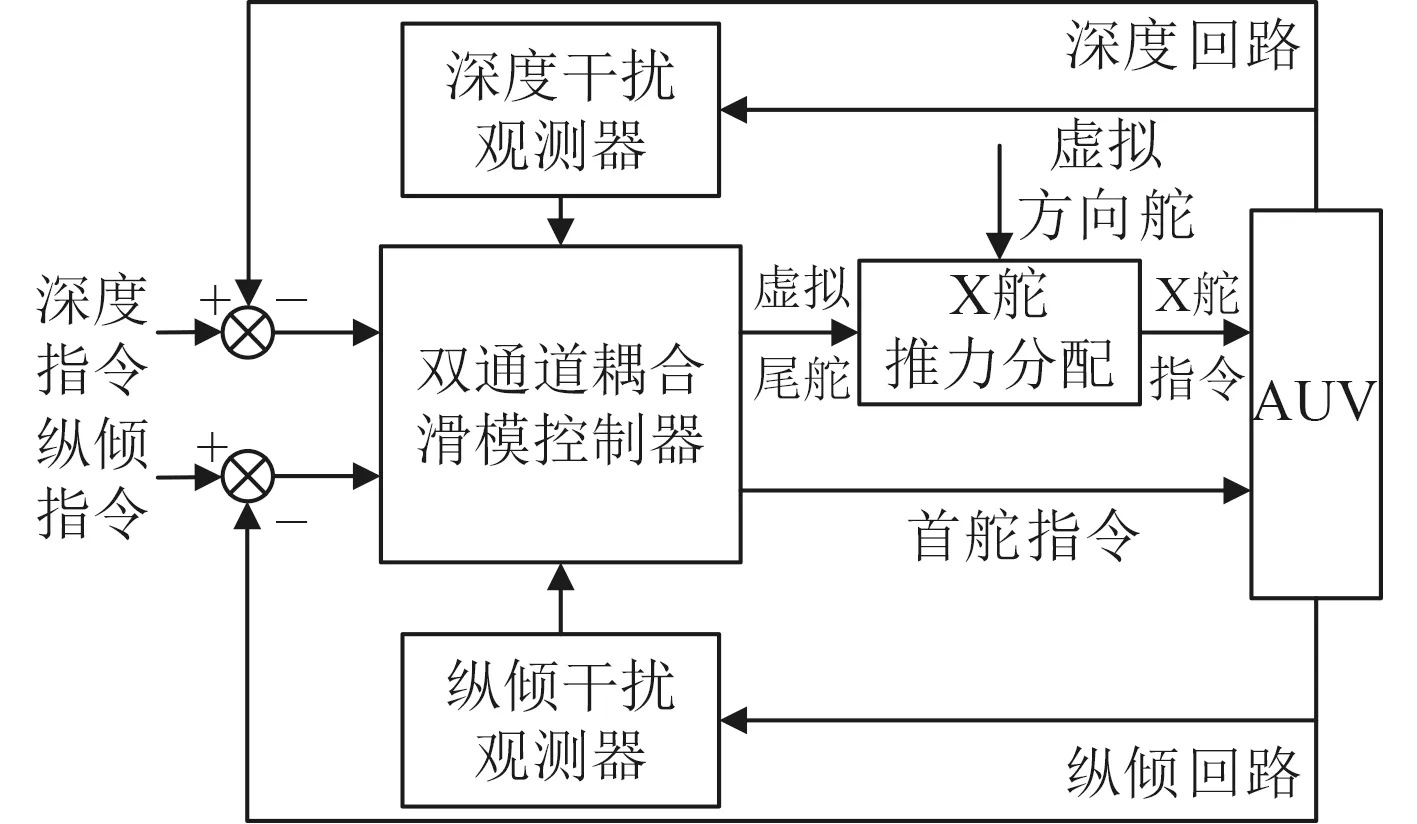
图1 控制器结构框图Fig. 1 Block diagram of controller

2.1 非线性干扰观测器设计

AUV在变深航行过程中，为了保持艇内人员的舒适性，纵倾角一般很小。因此可将式(1)转化为：

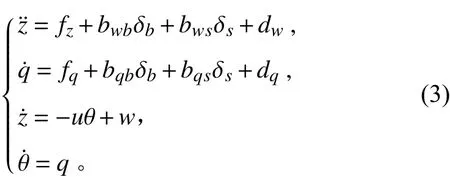
式中，f=-+f。

为了补偿AUV变深过程中深度与纵倾通道的耦合干扰与未建模动态，设计深度与纵倾通道的非线性干扰观测器如下式：

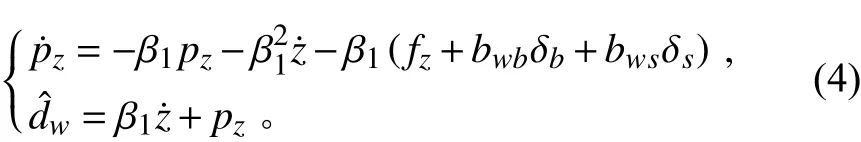
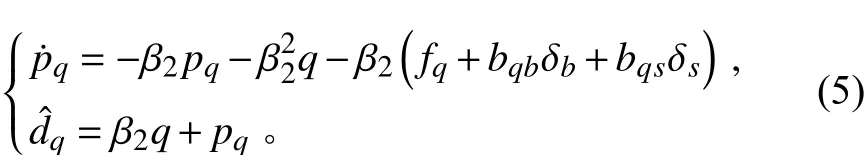
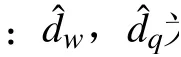
以深度通道为例，证明干扰观测器的收敛性。定义观测器误差˜=d-ˆ，考虑到AUV的变深航行是一个大惯性的慢过程，因此假设变深过程中观测器误差变化率ˆ=0，则观测器误差导数为：

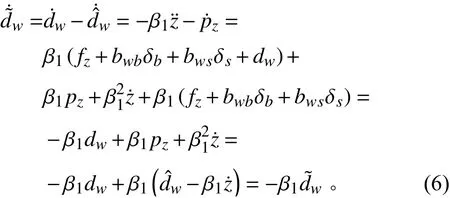
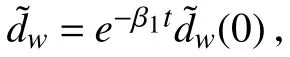
同理也可证得纵倾通道的非线性干扰观测器收敛。

2.2 滑模控制器设计

从式(3)可以看出，首舵与尾舵同时控制AUV的深度与纵倾。为了简化控制器设计，设计2个虚拟控制量对深度与纵倾通道进行解耦，2个虚拟量的表达式如下：

则式(3)可转化为：

以深度通道为例，定义深度与深度变化率的误差为：

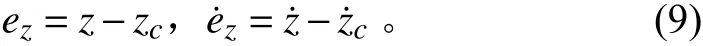
式中，z˙与z为深度与深度变化率指令。

定义线性滑模面为：

式中：c为可调参数，满足c＞0。

对式(10)求导得：

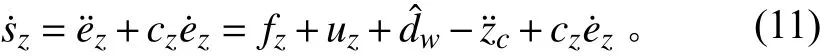
使˙s=0可得出滑模控制的等效控制率为：

在滑模趋近率方面本文选择指数型趋近率作为切换控制率：

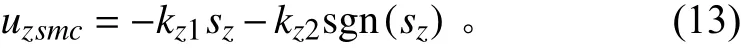
式中：，k为 滑模趋近率的参数，均为正常数；sgn(·)为符号函数。

因此滑模控制器最终的控制率形式为：

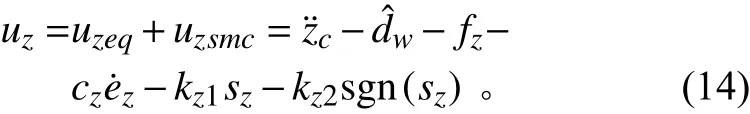
可以看出，由于控制率(14)中符号函数的存在，控制输出不连续，这便是滑模控制会出现控制器输出抖振的原因。为了消除抖振，这里引入饱和函数来替代符号函数：

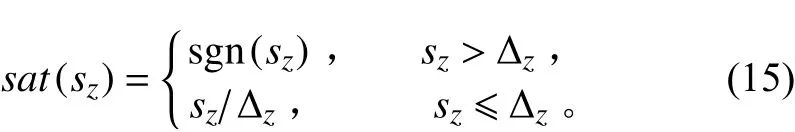
式中：Δ＞0为饱和函数的边界层厚度，则式(14)可转化为：

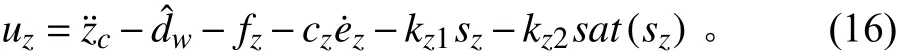
同理可得到纵倾通道控制率为：

2.3 舵角分配算法设计

在控制器解算出虚拟尾舵舵角指令后，下一步将把虚拟尾舵舵角指令分配到X舵的4个舵角上，X舵4个舵的编号如图2所示。

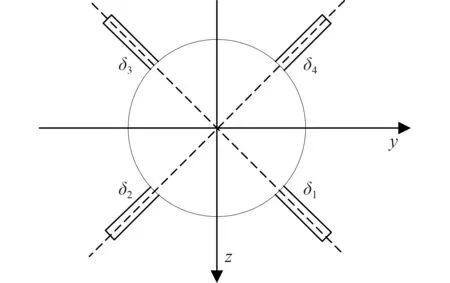
图2 X舵布局Fig. 2 Layout of the X-rudder

参考文献[8]，X舵角与十字舵角的转换关系为：

将式(18)转化为如下形式：

式中： τ=[δ,δ]， τ=[δ,δ,δ,δ]，控制效率矩阵为：

使用伪逆法设计X舵角分配算法，其表达式如下：

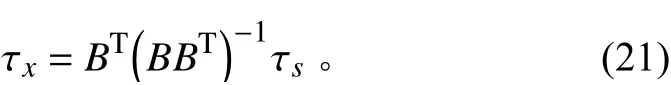
3 仿真验证

基于X舵六自由度操纵运动模型为被控对象，采用文献[9]的AUV模型参数，对控制器进行验证。为体现本文算法的控制性能，将其与PID算法的仿真结果进行对比。仿真条件为：AUV初始深度为30 m，航行速度为8 kn，目标深度为60 m；变深控制时不关注水平面的运动，因此在舵角分配时设置方向舵虚拟舵角为0，即 δ=0。仿真结果如图3～图9所示，其中NDO-SMC表示本文算法。

图3 深度响应曲线Fig. 3 The response curve of depth

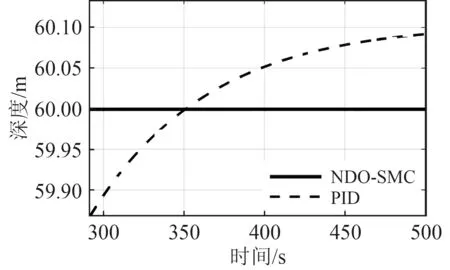
图4 深度曲线局部放大图Fig. 4 The detail view of depth curve

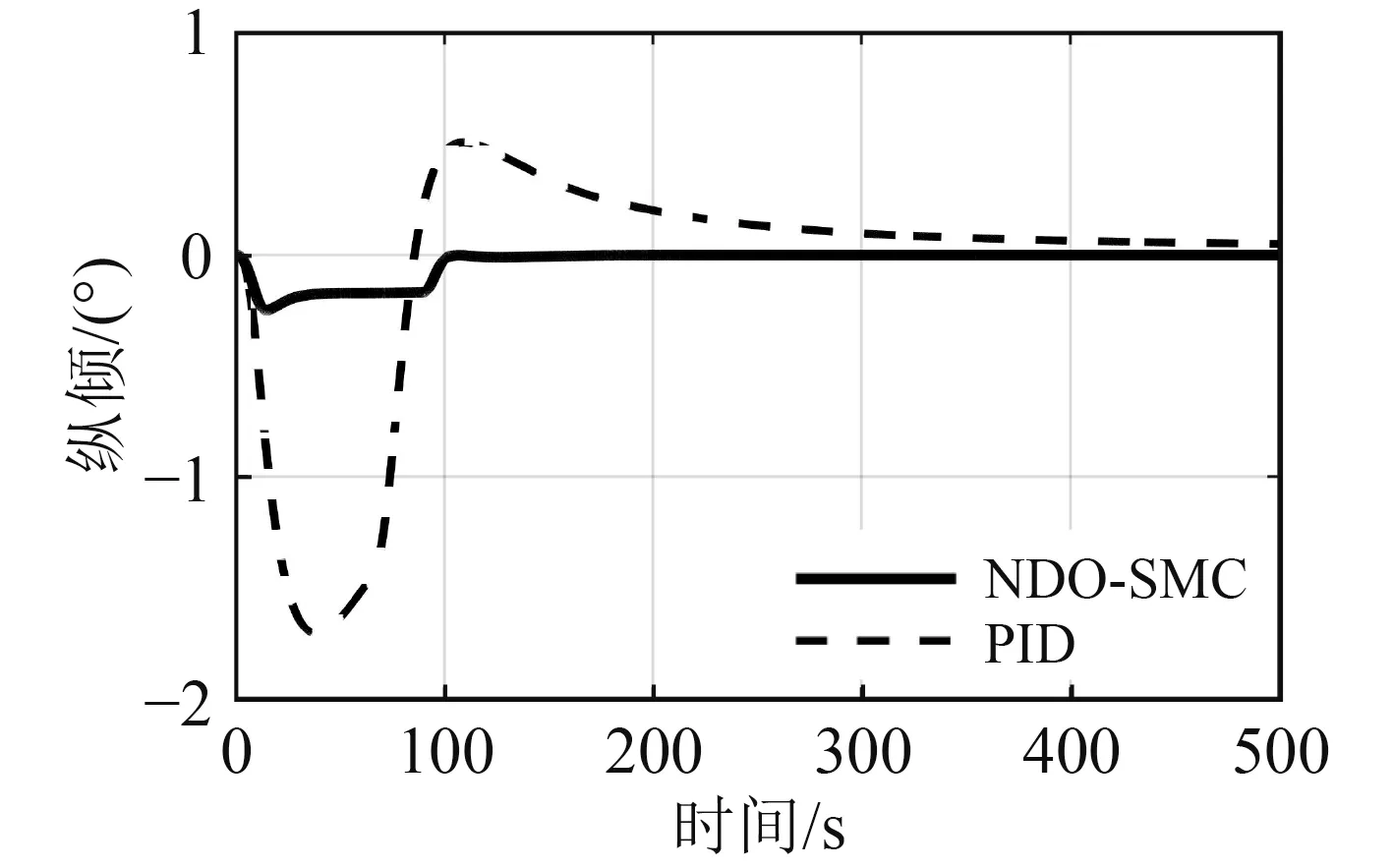
图5 纵倾响应曲线Fig. 5 The response curve of pitch

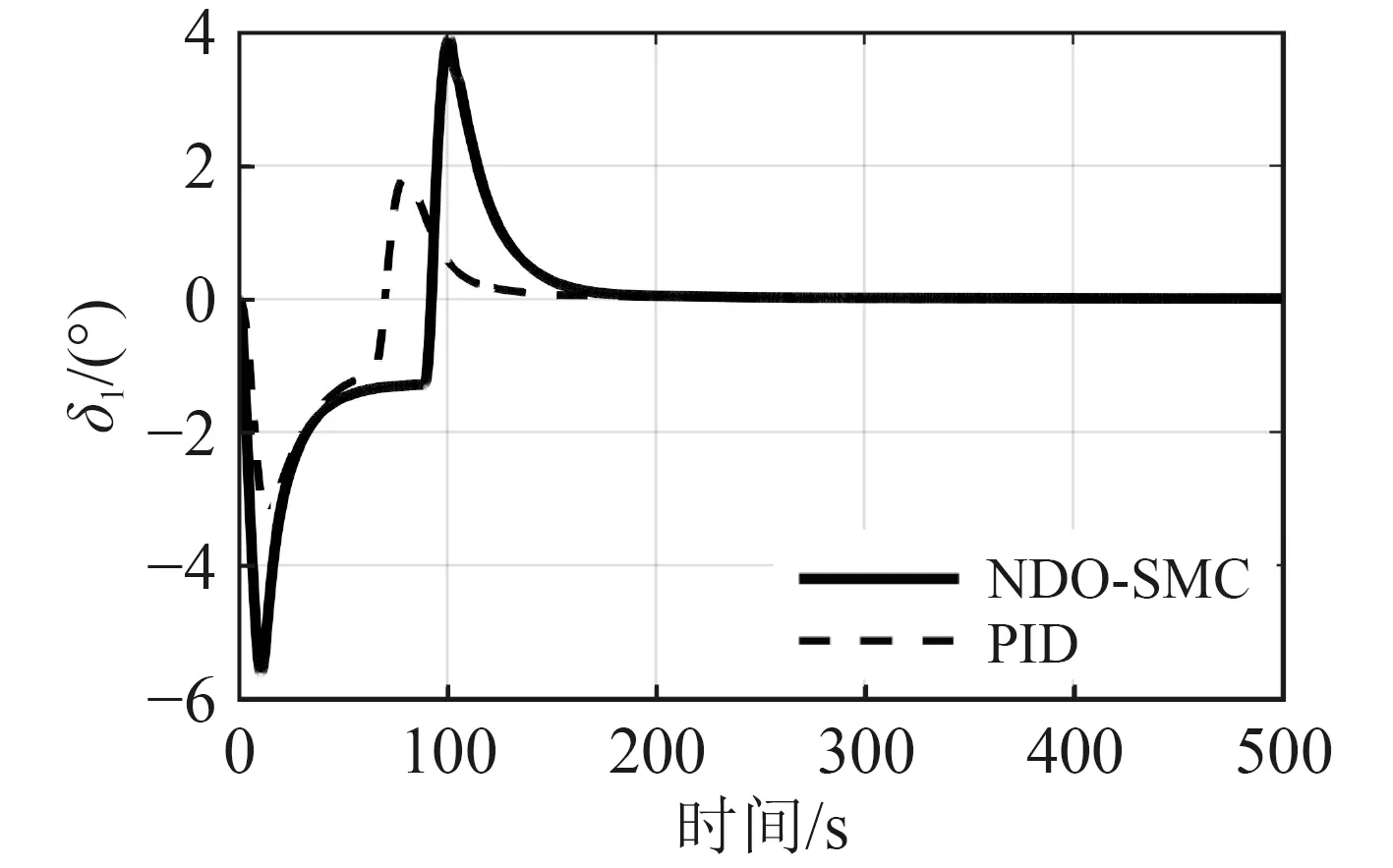
图6 舵角1响应曲线Fig. 6 The response curve of rudder 1

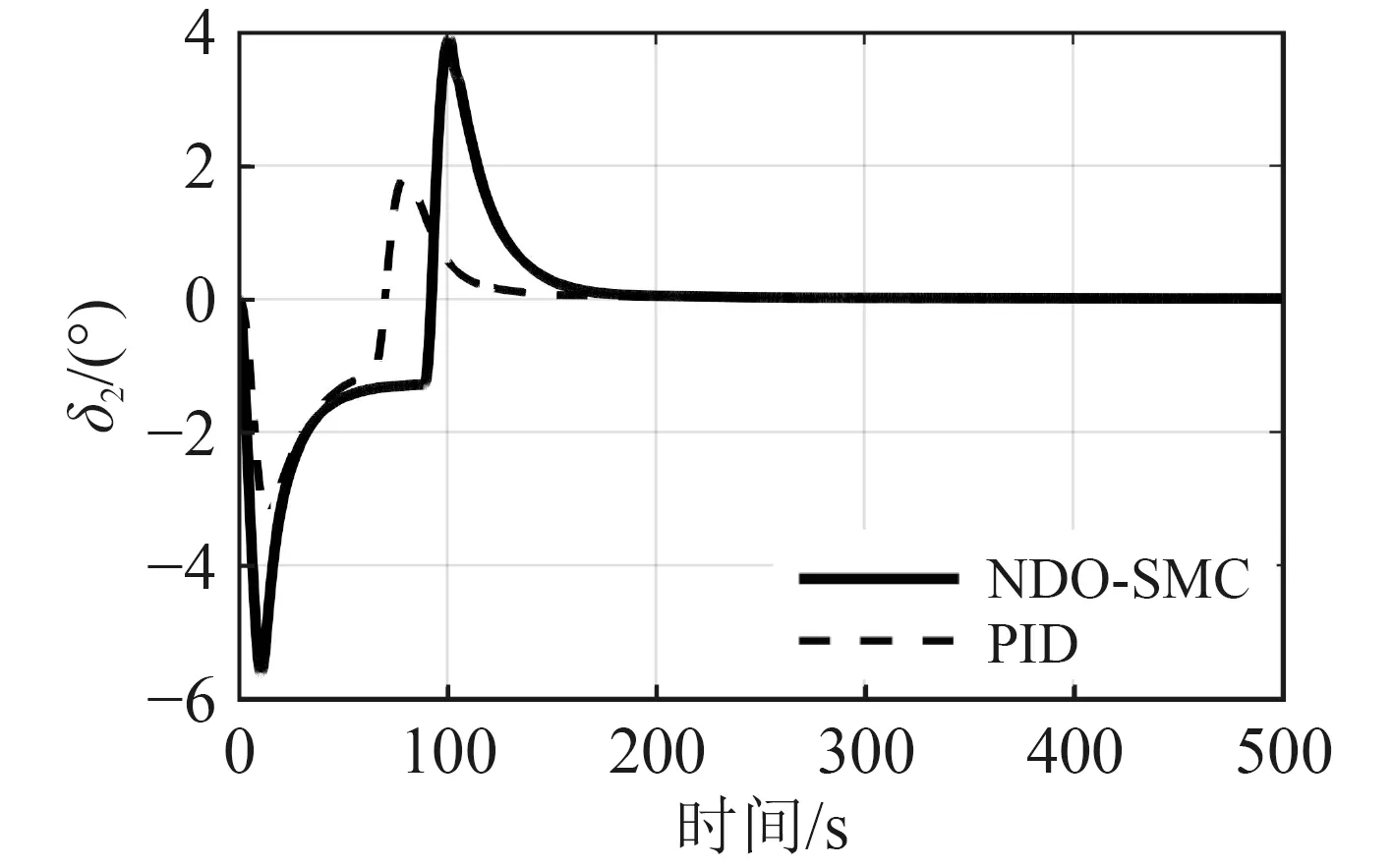
图7 舵角2响应曲线Fig. 7 The response curve of rudder 2

图8 舵角3响应曲线Fig. 8 The response curve of rudder 3

可以看出，2种控制算法均能够使X舵AUV完成变深控制，证明了本文所设计舵角分配算法的有效性。

从图3可以看出，PID控制器在初期有很快的响应速度，在90 s左右收敛速度放缓，而NDO-SMC控制器虽然在初期响应速度不如PID，但在150 s左右已收敛到指定深度，因此相比与PID控制器，NDO-SMC控制器深度收敛速度更快；从图4中的深度曲线局部放大图可以明显看出，相比与相比与PID控制器，NDOSMC控制器有着更高的深度控制精度。

图9 舵角4响应曲线Fig. 9 The response curve of rudder 4

从图5的纵倾响应曲线可以看出，NDO-SMC控制器使纵倾角在100 s左右收敛到0，调节过程中最大纵倾角为-0.25°，整个过程几乎保持零纵倾变深，而PID控制器使AUV在变深时最大产生了-1.7°的纵倾角，且纵倾收敛速度较慢，因此相比PID控制器，NDO-SMC控制器有着更强的纵倾控制能力。

从图6～图10的舵角响应曲线可以看出，相比PID控制器，NDO-SMC控制器的动舵幅度更大，舵利用率更高，更好地发挥了操舵系统的控制性能。

图10 首舵响应曲线Fig. 10 The response curve of bow rudder

4 结 语

本文针对X舵AUV的零纵倾变深控制问题，设计一种基于非线性干扰观测器的滑模控制器，并采用伪逆法将控制器产生的舵角指令分配到X舵的4个舵角。仿真结果表明，相比PID控制器，本文控制器能够有效地提高变深控制中深度与纵倾的控制精度与收敛速度，能够有效控制X舵型AUV零纵倾平稳变深航行。