可视化编程在程序设计课程教学中的应用

白小军，卢颖

（西安工业大学 计算机科学与工程学院，西安 710021）

计算机程序设计是高校理工科专业普遍开设的一门基础课，目标是引导学生理解编程的思想和方法，并掌握一门语言工具以编程解决实际问题。近几年来，随着计算思维理念的发展，用计算学科的方法和工具来解决各专业领域的实际问题已成为一种趋势，程序设计课程的重要性越来越凸显出来。

然而在实际教学中，要实现课程的目标却并非易事。首先，要学好该课程，学生需要投入大量的精力去编写和调试程序，很多时候学生会对繁琐的语法规则望而生畏，并因为程序无法运行而对编程失去信心；其次，编程的过程是一个逻辑思维的过程，而很多学生在刚入校时逻辑思维能力还有所欠缺，需要一个循序渐进的培养过程；另外，程序设计课程中通常使用流程图来表达算法逻辑，但这种方式验证性差，难以看到执行结果，无法验证算法的正确性。

近年来出现了很多可视化编程工具，最典型的有Scratch、Blockly、Snap等。在程序设计课程中引入可视化编程，可以有效解决上面提出的问题。首先，计算思维的核心是思想方法而不是繁琐的语法，使用可视化工具可以简化编程，使学生注意力集中到程序逻辑上而不是语法规则上，有助于克服畏难情绪；其次，可视化编程能够将程序逻辑清晰地展现出来，编程的过程就是逻辑思维锻炼的过程；最后，使用可视化工具建模，设计好算法后能够立刻跟踪算法的执行过程并看到结果，方便验证算法。

一、可视化编程在课堂教学中的应用

课程教学中，可在三个层面使用可视化编程：第一是算法层面，使用可视化程序代替流程图，直观地介绍常用算法的逻辑，并立刻进行验证；第二是在编码层面，结合编程语言的语法规则、控制结构等，将可视化程序转化为相应语言的代码，帮助学生实现从算法逻辑到程序代码的转换；第三是在模块化层面，采用自定义积木的方式创建程序模块，帮助学生理解模块化设计的思想。

（一）使用可视化编程理解基本算法设计

算法是程序的灵魂，也是培养学生计算思维、逻辑思维的根本。在课程开始阶段，使用最简单、有趣的工具展示算法设计，容易引起学生兴趣。笔者在实践中首先使用Scratch，其既提供基于网页的在线版本，也提供离线安装版本。该系统面向的目标首先是中小学生，设计的卡通形象和舞台效果很吸引人，对大学新生也有足够的吸引力。

在算法设计中，针对顺序、选择、循环及混合的处理逻辑，分别选取典型案例，用Scratch 积木可视化呈现，能起到良好的演示效果。

在顺序结构部分，选用鸡兔同笼问题，让学生理解从问题到程序的转换过程，“输入—处理—输出”的程序流程，以及变量、表达式等基本概念，如图1 所示。在选择结构部分，采用“输入3 个数并输出最大值”的示例，说明算法的流程结构，并以“if”及“if-else”等基本结构块来实现算法，如图2 所示。

图1 鸡兔同笼问题的算法

图2 求3 个数最大值的算法

图3 从1 累加到100 的算法

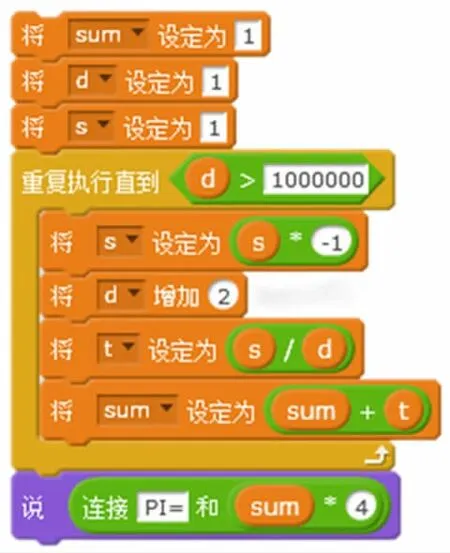
图4 求π 值的算法

为帮助学生理解数组这一基本数据结构，设计“输出Fibonacci 数列的前20 项”的示例，如图5（a）所示，在循环结构中，演示了Fibonacci 数列的生成过程，同时，舞台上的变量和数列显示如图5（b）所示，能够直观地看到数组数据的组织及访问方式。

图5 生成Fibonacci 数列的算法

可以看出，采用可视化工具代替流程图来描述算法，不但简单、直观，而且能够立刻执行、验证，利于学生理解算法逻辑和数据组织方式。

（二）通过可视化编程理解高级语言代码

可视化程序的构造块和高级语言的语句都是对计算机指令执行过程的高级抽象，两者间具有相似性，只要学习了高级语言的语法规则和控制结构，就能很容易地将可视化程序转化为高级语言代码。以图2 和图4 为例，转化为C 语言代码分别如图6 和图7 所示。

图6 输入3 个数求最大值的代码

图7 根据公式求π 值的代码

这种编程训练在课堂教学中可以分两步来实施，首先由教师主导，提出问题并设计可视化程序，引导学生理解算法逻辑；然后由学生动手，根据语法规则和程序结构，将可视化程序转化为具体的语言代码，完成从算法逻辑到高级语言程序的转换。在设计可视化程序的过程中，可以引出变量及其存储方式、运算符、表达式、流程控制和输入输出等概念，而这些概念在转化程序时又可以方便地映射到高级语言的语法规则中。通过这一分解，将原来复杂的编程问题转化为2 个相对简单的步骤来完成，利于学生克服畏难情绪，也利于抓住编程的要点。

（三）通过可视化编程理解模块化设计

模块化编程是程序设计课程的核心内容之一，高级语言中一般都通过函数来实现模块化设计。Scratch 难以模拟高级语言中函数的功能，所以需要一套更加强大的可视化编程工具。笔者采用功能更加强大的可视化编程工具Snap，其提供基于Web 的编程环境，可视化程序可以保存在客户端或云端；且支持常用的数据类型，完全支持模块化开发，甚至允许创建新的控制结构，能够完美地用于程序设计课程的教学。

Snap 采用自定义积木的方式制作程序模块，例如，为求一组数据中的最大值，设计如图8 和图9 所示的程序。其中，第一个积木块定义了函数的原型，函数名为getArrMax，需要传递进来一个数组s 作为参数，并返回一个数据m 作为最大值；中间部分定义了求最大值的算法，首先假定数组第一项为最大值，存入变量m，其后循环遍历所有的数组元素，当发现某项值大于m 时，用其替换m 值，这样循环结束时，m 中存放的就是数组元素的最大值；最后一个积木块向主调程序返回数据，相当于高级语言中的return 语句。主调程序如图9 所示，其核心部分（第三个积木块）调用了自定义的函数求数组中的最大值。

图8 求最大值的自定义模块

图9 求数组最大值的主程序

图10 求组合数的自定义模块

图11 求阶乘的自定义模块

递归是计算学科中一种独特的思想方法，即：一个函数可以直接或间接地调用自身，前提是必须满足三个基本条件：（1）有一套递推公式；（2）每次递推后函数的运算规模都会减小；（3）当递推到一定条件时找到出口。例如，对求阶乘的函数进行改造，设计如下的递推公式，就可以采用递归算法来实现。改造后的求阶乘函数如图12 所示。

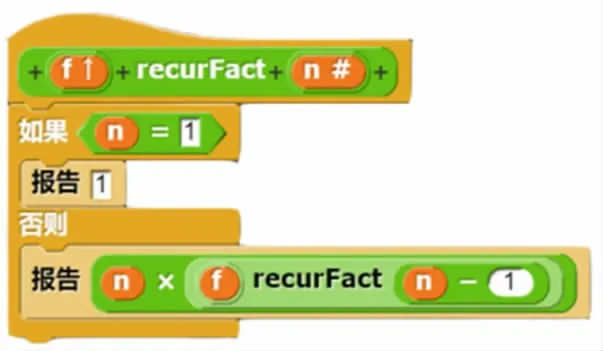
图12 求阶乘的递归算法

通过以上示例，可以直观地展示模块化设计中的核心概念和思想方法。

二、可视化编程在实践教学中的应用

在该课程的实践教学中发现，很多学生的编程能力始终跟不上课程节奏，直到课程结束，也难以独立完成较复杂的程序。究其原因，一是程序的逻辑较为抽象，学生没有理解程序的执行过程，难以正确地设计程序结构；二是高级语言的语法规则较为繁琐，学生将大量精力都浪费在了处理语法错误上。而当这两个问题交织在一起的时候，调试程序的难度就急剧上升，学生很难定位错误到底出在哪里，所以每次实践课程的收获都很有限，很多同学仅限于将教材上的代码搬进计算机，使之运行起来，而独立编写和调试代码的能力明显不足。

引入可视化编程，将复杂的问题分解为两步完成。第一步，根据实践任务进行可视化设计，深入理解程序逻辑，并且直观地观察程序的运行过程，相互对照，熟练掌握程序结构；第二步，将可视化程序转化为高级语言代码，并上机调试。这样分解的好处在于解耦了程序逻辑错误与语法错误之间的关系，更容易发现和解决问题。

以选择排序算法为例，在课堂讲解时帮助学生理清算法思路，并独立完成可视化程序设计，如图13 所示，该模块在数组元素值互换的代码块中加入1 秒延时，运行程序时观察数组变量，可以清楚地看到每一轮迭代中元素的互换和移动，便于理解算法逻辑。当可视化程序调试成功后，可以确保算法逻辑没有问题，这时进入第二步，转化高级语言代码，由于可视化构造块与高级语言语句块之间很大程度上有对应关系，所以这种转化相对来说难度不大。基于以上步骤，学生对程序的理解更加深刻，也更容易编写和调试程序。

图13 选择排序的可视化算法

三、结束语

笔者将可视化编程引入本科生计算机程序设计课程的教学，从算法逻辑、代码转换和模块化设计三个方面展开研究，在课堂教学和实践教学中进行了尝试。从教学效果来看，学生的学习兴趣得到了提高，不再畏惧编写代码，逻辑思维得到了锻炼，能够熟练地描述算法逻辑并进行验证，阅读程序和编写程序的能力得到了明显改进，对程序的理解上了一个台阶。实践证明，引入可视化编程，能够有效改进课堂教学和实践教学的效果。