核心素养背景下应用型本科高校线性代数实验教学研究
史雪莹,陈小平
(泰州学院 数理学院,江苏 泰州 225300)
二十一世纪以来,由于全球经济迅猛发展,全球信息化和知识经济等对教育提出了新要求,各国为应对信息时代所带来的挑战,相继推出具有时代意义的发展方向——核心素养。我国教育部2014 年发布的文件中第一次提出了“核心素养体系”的概念,并于2016 年正式发布了核心素养框架。2019 年,教育部关于高校招生工作通知中强调要考察学生的关键能力和学科素养。另外,教育部发布的文件中指出本科课程要加强以核心素养为导向,杜绝单纯知识的传递,重视学生数学思维方式、数学思想方法和问题解决行为等数学素养核心维度的培养。由此,核心素养导向的课程建设探索与实践已成为我国各高校进行教学改革的重要内容之一。
众所周知,核心素养导向教育包含如下两个特点:核心素养导向教育的教学目标需明确,即培养既有品格又有能力的高素质应用型人才;核心素养导向教育的教学方式应重视理论教学与实践教学相结合,注重立德树人,特别是培养学生运用理论知识解决实际问题的能力。因此,应用型本科高校在落实核心素养导向教育的实践中需强化实践教学,并加强各课程在实际中的应用研究。我们知道,线性代数在图像处理、机器学习等领域都有着广泛应用。教师在讲授线性代数理论知识的同时,还需激发学生学习线性代数的热情,培养学生的创新思维,加强本课程在实际生活中的应用研究。目前利用数学软件完成问题分析与计算已被应用于大学数学课程的教学,所以强调数学软件在线性代数教学中的应用已被各应用型本科高校高度重视。
近年来,国内不少学者在线性代数教学改革与实践方面作了许多探索,特别是如何将专业数学软件应用于线性代数教学做了许多尝试和教学改革。魏岳嵩等探讨了如何处理好软件教学与传统教学的关系,给出了软件教学的内容与安排及相应的教学建议。孟国艳等针对线性代数的教学过程中实践教学不足的问题,提出了课程教学活动中融合数学建模的思想并给出了具体策略。杜红林以特征值教学为例,给出了Matlab 辅助教学的具体过程,这样能使学生更清晰地理解特征值和特征向量的几何意义。刘小刚等阐述了如何将Maple 软件应用于线性代数课程教学与实践。
我们知道,向量和线性方程组是线性代数中的重要内容,其被广泛应用于解决密码学、计算机图形学和最优化等方面的问题。一般来说,线性代数教材中的例题都比较简单,矩阵的阶数也比较小,易于手工计算,但教师若想解决实际问题,面对规模较大的数据,这时仍用手工进行计算往往是无法实现的。这里将Matlab 引入到线性代数的教学就可轻松解决上述问题,另外也可为小规模矩阵相关的手工计算提供一条检验途径。因篇幅有限,下面以线性方程组和向量为例,结合本校相关专业给出如何利用Matlab 开展线性代数实验教学。
一、利用Matlab 求解线性方程组


所以上述齐次线性方程组的基础解系为η=(3,-4,1,0),η=(-4,5,0,1)。于是,原方程组的通解为x=t(3,-4,1,0)+t(-4,5,0,1),其中t,t为任意常数。
注:类似例1,请读者自行编写Matlab 程序讨论k为何值时,齐次线性方程组

有非零解,并在有非零解时求其基础解系。


其中t,t为任意常数。
注:类似例2,读者参考上述过程利用Matlab 自行编写程序讨论k 为何值时,线性方程组
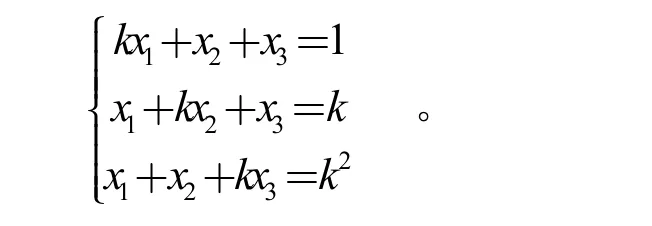
无解、有唯一解和无穷多解?
二、利用Matlab 判定向量组的线性相关性
例3 求向量组x=(3,1,2,5),x=(1,1,1,2),x=(2,0,1,3),x=(1,-1,0,1),x=(4,2,3,7)的秩和一个极大无关组,并用所求的极大无关组表示其余向量。

所以向量组的秩为2,第一列和第二列x,x为极大线性无关组,根据行最简形A 知:x,x,x可用极大无关组x,x线性表示,具体如下

例4 向量b=(1,4,0)能否由向量组a=(1,3,1),a=(1,-1,5),a=(-3,-3,-9),a=(-1,4,-8)线性表示?若可以,给出具体线性表达式。
分析:本题目相当于判定线性方程组(a,a,a,a)x=b 是否有解,如果上述方程组有解,那么其解就是线性表达式的系数。


有了上述利用Matlab 开展实验教学的基础,线性代数教学过程中还可融入一些体现数学建模思想的实际案例,这样可让学生真实地感受到线性代数课程是源于实践、用于实践的。当然,案例的选取既要符合本课程教学目的和内容要求,还需考虑不同专业学生的特点,体现专业方向,表1 罗列了泰州学院教师在讲授线性方程组和向量这一部分内容时的部分教学案例,仅供参考。

表1 线性代数课程融入数学建模思想的部分教学案例
本文结合自身实际教学通过具体实例阐述了如何将Matlab 应用于线性代数中线性方程组和向量的实验教学。从上述实例可知,基于Matlab 的实验教学能高效求解规模较大的线性方程组及判定多个向量的线性相关性,同时对提升应用型本科高校学生分析与解决实际问题的能力,以及激发学生的学习积极性都有着重要的促进作用。

